Похожие презентации:
Правильные многоугольники
1. Правильные многоугольники.
МОУ лицей №239 класс
09.02.2008
г.Калининград.
Шульц И. А.
2. Самостоятельная работа:
1 Вариант2 Вариант
№1. Найдите углы правильного
восьмиугольника
двенадцатиугольника.
№2. Сколько сторон имеет правильный многоугольник, если
каждый его угол равен
1440
1560.
№3. Сколько сторон имеет правильный многоугольник, если
внешний угол
внутренний угол
меньше внутреннего
относится к внешнему
в 11 раз?
как 13:2?
3. Повторение теории:
Многоугольник называется правильным, если…Многоугольник называется вписанным в
окружность, если…
Многоугольник называется описанным около
окружности, если …
аn=…
S=…
r =…
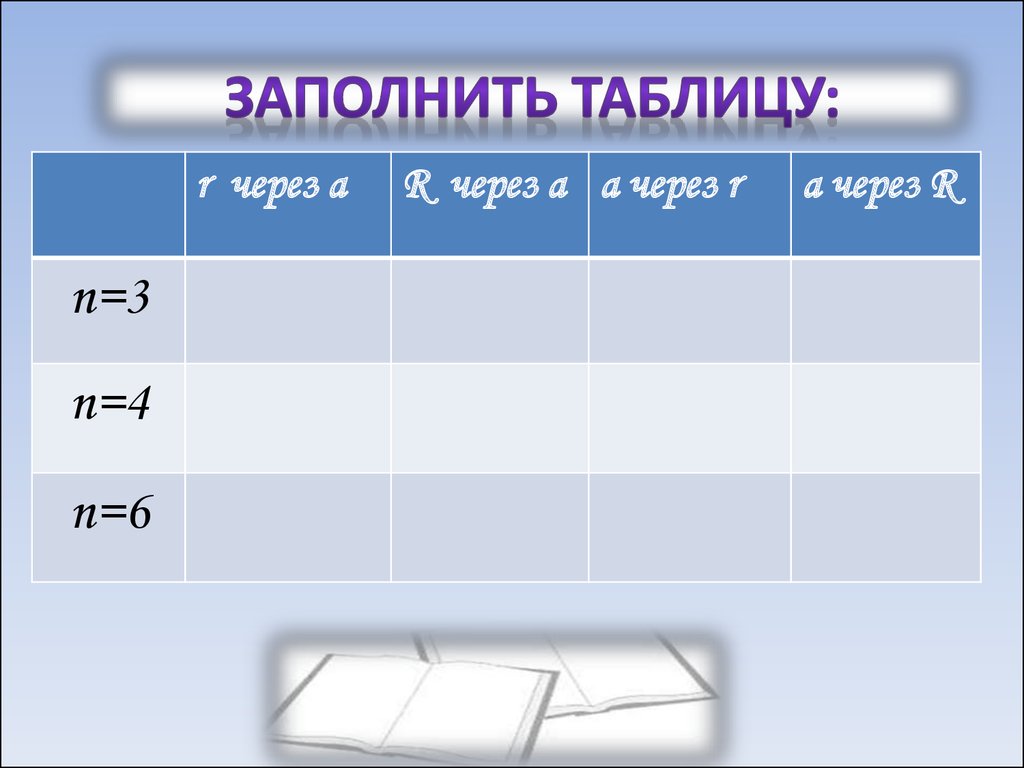
4. Заполнить таблицу:
r через аn=3
n=4
n=6
R через а а через r
а через R
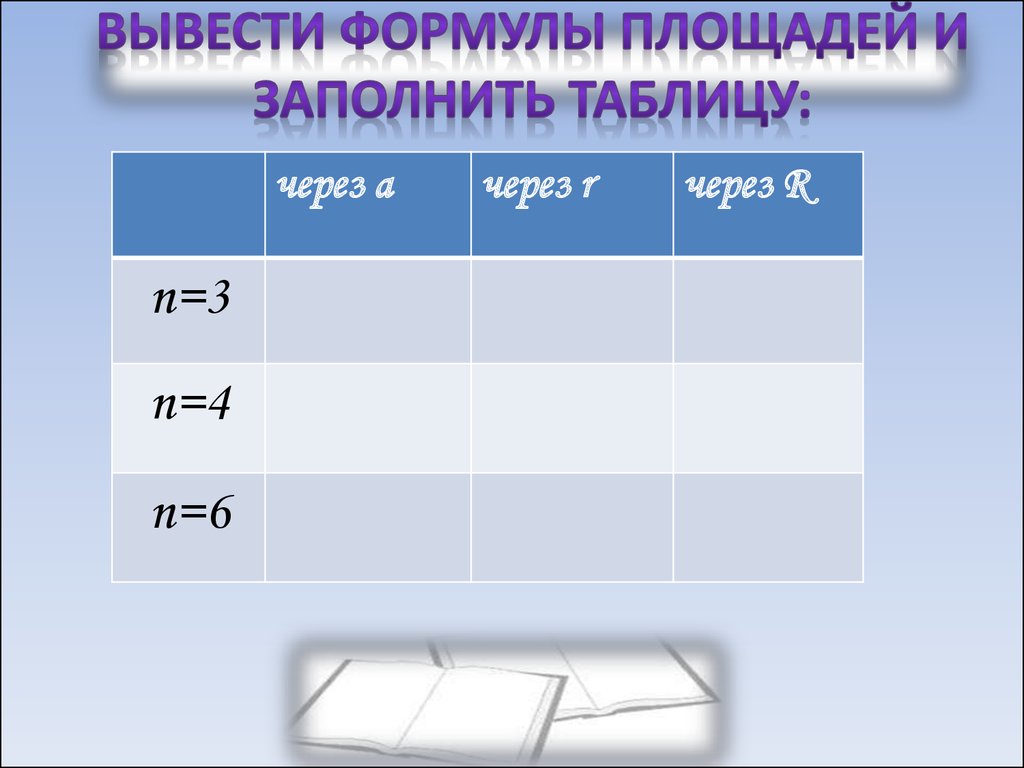
5. Вывести формулы площадей и Заполнить таблицу:
через аn=3
n=4
n=6
через r
через R
6.
Найдите величину центрального углаправильного девятиугольника.
?
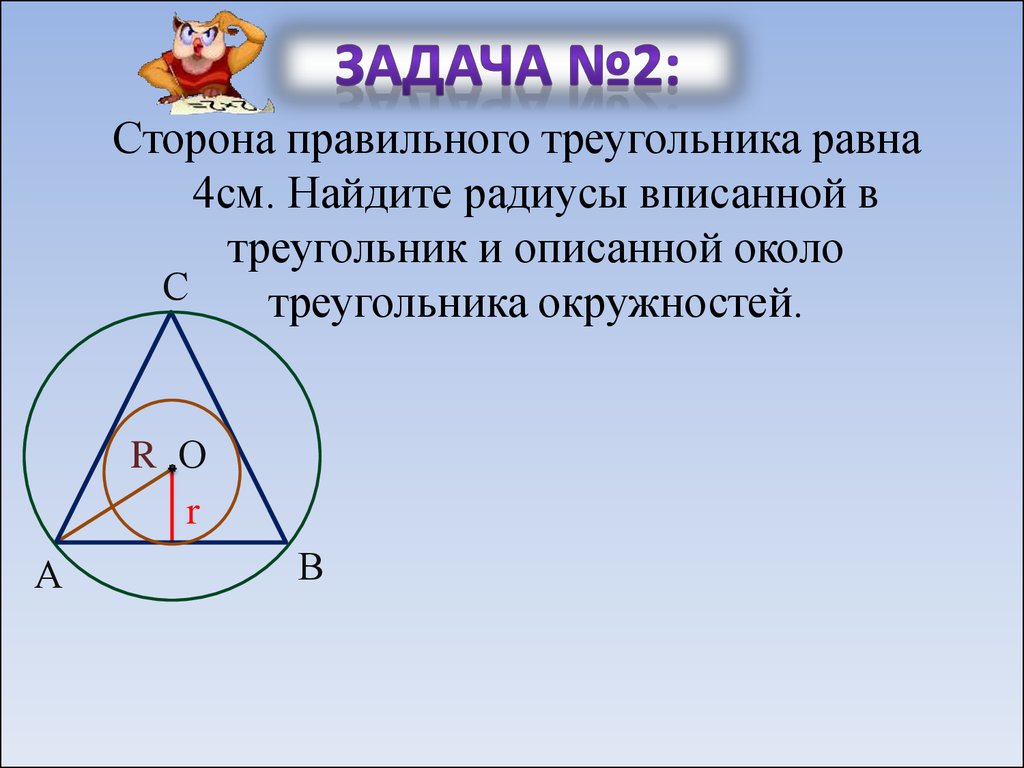
7. Задача №2:
Сторона правильного треугольника равна4см. Найдите радиусы вписанной в
треугольник и описанной около
С
треугольника окружностей.
R О
r
А
В
8.
Найдите сторону правильного четырехугольника ирадиус вписанной в него окружности, если
радиус, описанной окружности равен 5 2 .
5 2
9.
Найти сторону и радиус окружностиописанной около правильного
шестиугольника, если радиус вписанной в
него окружности равен 4 3.
4 3
10.
Правильный треугольник со стороной 6вписан в окружность. Найдите сторону
правильного четырехугольника,
вписанного в эту же окружность.
11.
Найти отношение сторон правильныхшестиугольников: вписанного в окружность
и описанного около неё.
12.
Около квадрата со стороной 6см описанаокружность, около окружности описан
правильный шестиугольник. Найти радиус
описанной около шестиугольника
окружности.
13.
Найти радиусы окружностей: вписанной вправильный шестиугольник и описанной
около него, если их разность равна 4см.
14.
Найти площадь правильного треугольника,если радиус, описанной около него
окружности равен 7см.
R
15.
Площадь квадрата, описанного околоокружности 16см2. Найдите площадь
правильного треугольника, вписанного в
эту же окружность.












 Математика
Математика








