Основные понятия тригонометрии

1.

1
ГЛАВА 4

2.

2

3.

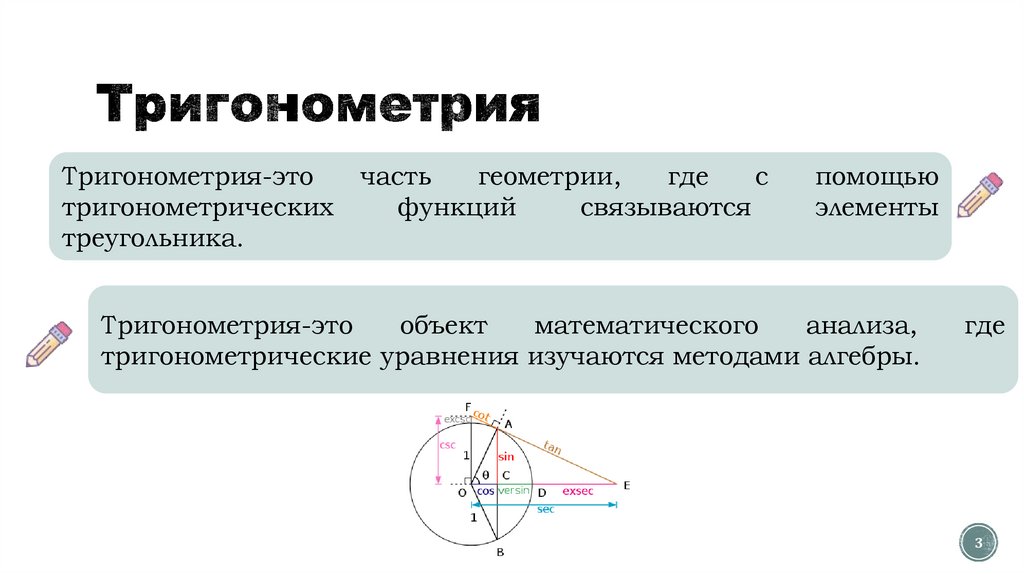
Тригонометрия-это
тригонометрических
треугольника.
часть
геометрии,
где
с
функций
связываются
помощью
элементы
Тригонометрия-это
объект
математического
анализа,
тригонометрические уравнения изучаются методами алгебры.
где
3

4.

Тригонометрия в древности являлась вспомогательным
разделом
астрономии.
Древнегреческие
разработали «тригонометрию хорд».
ученые
Древнеиндийские ученые заменили хорды синусами.
В
VIII
веке
математики
Востока
превратили
тригонометрию в самостоятельную математическую
дисциплину.
Ими
были
введены
другие
тригонометрические функции и составлены таблицы.
Окончательный вид тригонометрия приобрела в XVIII веке
в трудах Л.Эйлера.
4

5.

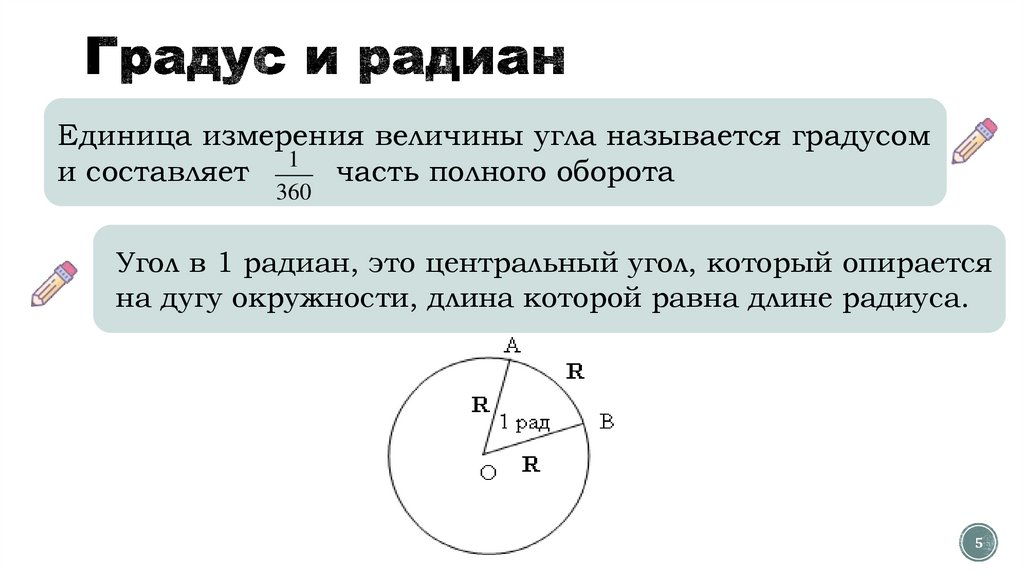
Единица измерения величины угла называется градусом
и составляет 1 часть полного оборота
360
Угол в 1 радиан, это центральный угол, который опирается
на дугу окружности, длина которой равна длине радиуса.
5

6.

360 180
1 рад
57 , 2958
2
1
180
0, 017453 рад
n
n
180
n n
180
6

7.

Перевести градусы в радианы: а)15○ б) 120○ в) 270○ г) 90○
а)
15
180
12
б)
120
180
2
3
в)
270
Перевести градусы в радианы: а)
180
а)
30
6
б )
180
180
6
180
3
2
б)
г)
90
180
2
3
в)
4
3 180
в)
135
4
7

8.

Перевести градусы в радианы:
I вариант
а)30○ б) 150○ в) 180○ г) 225○
II вариант
а)45○ б) 240○ в) 360○ г) 315○
Перевести градусы в радианы:
I вариант
II вариант
а)
5
б)
в) 5
4
6
а)
6
3
б)
в) 2
4
8

9.

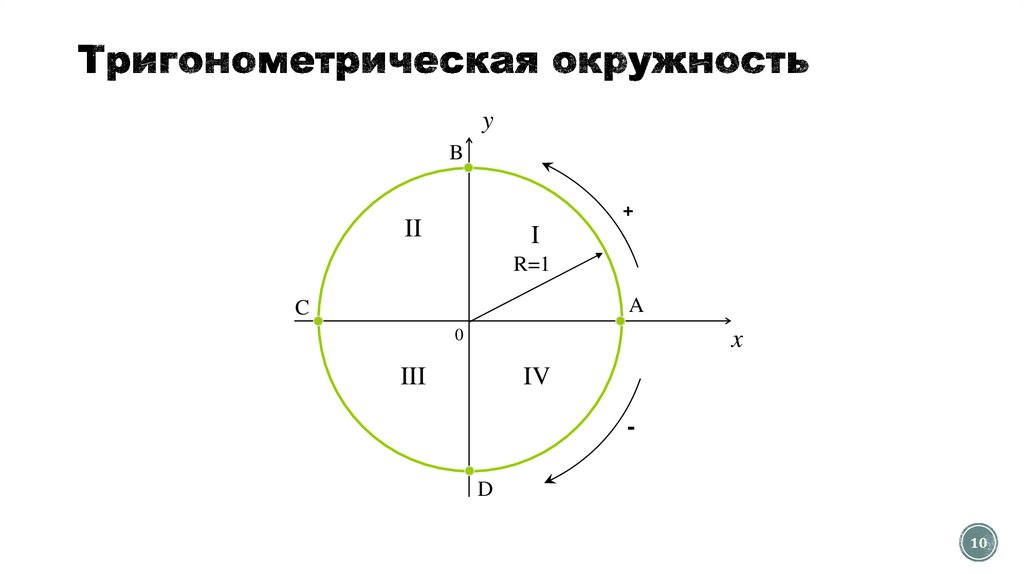
9

10.

y
B
+
II
I
R=1
A
C
0
x
III
IV
D
10

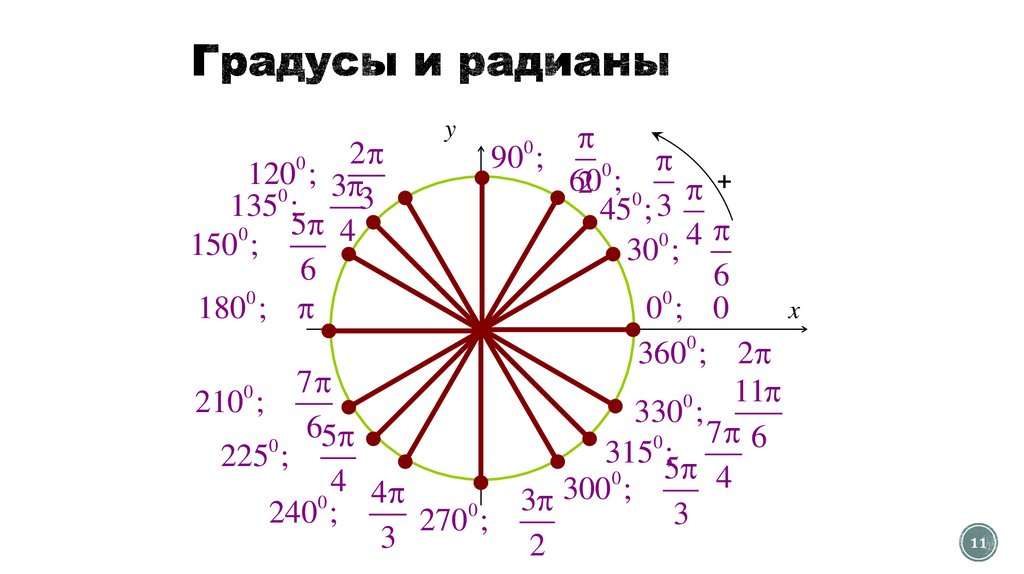
11.

2
90
;
0
0
120 ; 3
60
;0 +
2
0
3
3
135 ;
45
;
5 4
0
0 4
150 ;
30 ;
6
6
x
00 ; 0
1800 ;
0
0
360 ; 2
7
0
11
0
210 ;
330
;
65
7 6
0
0
315 5;
225 ;
0
4
4 4
300
;
3
0
2400 ;
3
270 ;
3
2
y
0
11

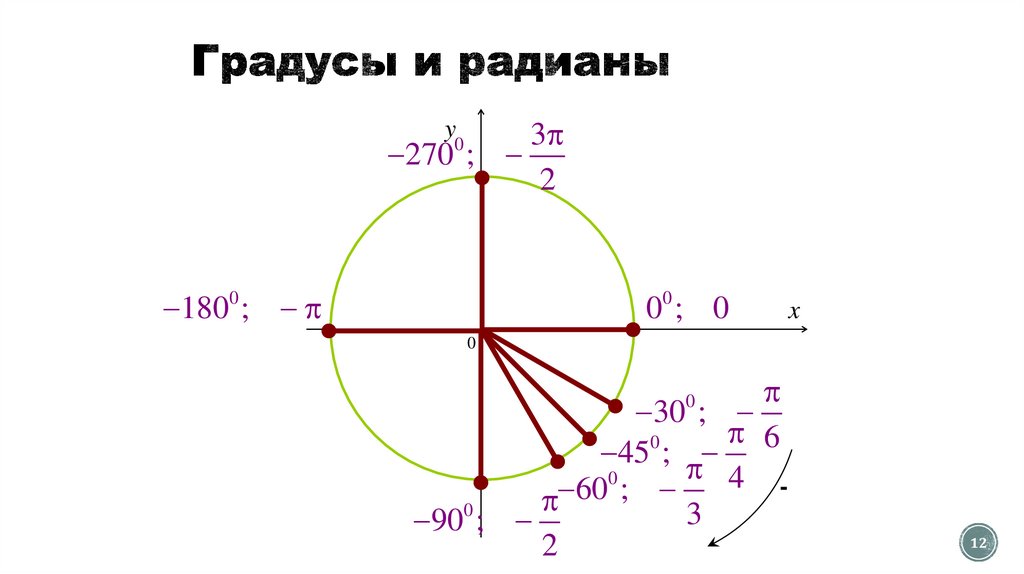
12.

3
270 ;
2
y
0
1800 ;
00 ; 0
x
0
30 ;
6
0
45 ;
0
4
60
;
0
3
90 ;
2
0
12

13.

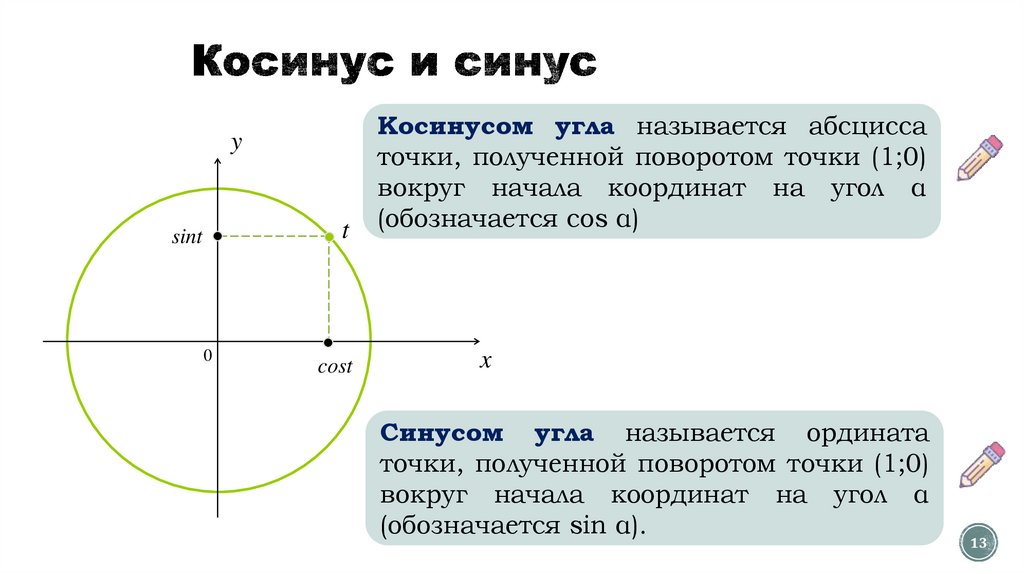
y
t
sint
0
cost
Косинусом угла называется абсцисса
точки, полученной поворотом точки (1;0)
вокруг начала координат на угол α
(обозначается cos α)
x
Синусом угла называется ордината
точки, полученной поворотом точки (1;0)
вокруг начала координат на угол α
(обозначается sin α).
13

14.

y
t
I
II
0
III
tgt
0
IV
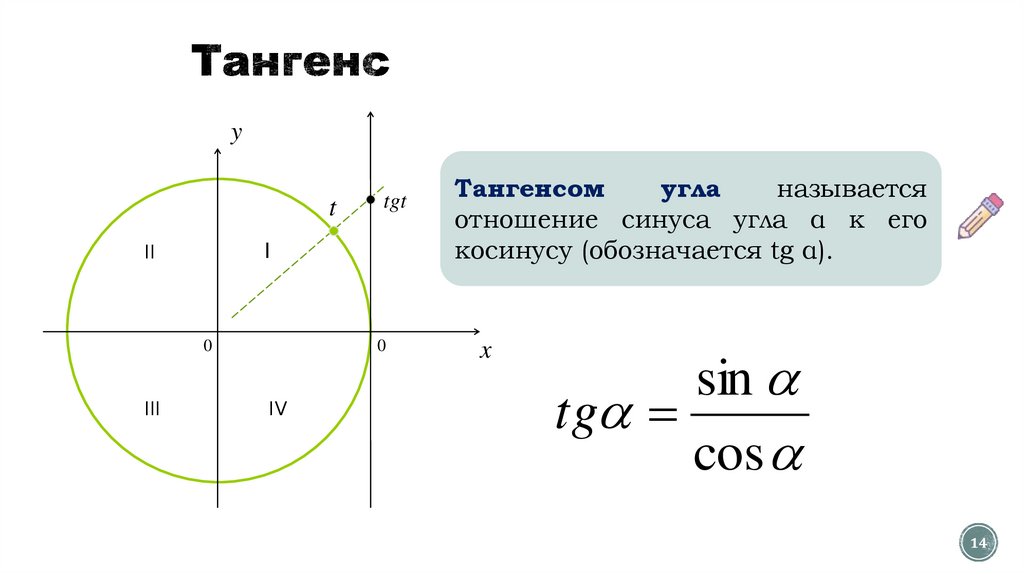
Тангенсом
угла
называется
отношение синуса угла α к его
косинусу (обозначается tg α).
x
sin
tg
cos
14

15.

y
ctgt
0
t
II
I
0
III
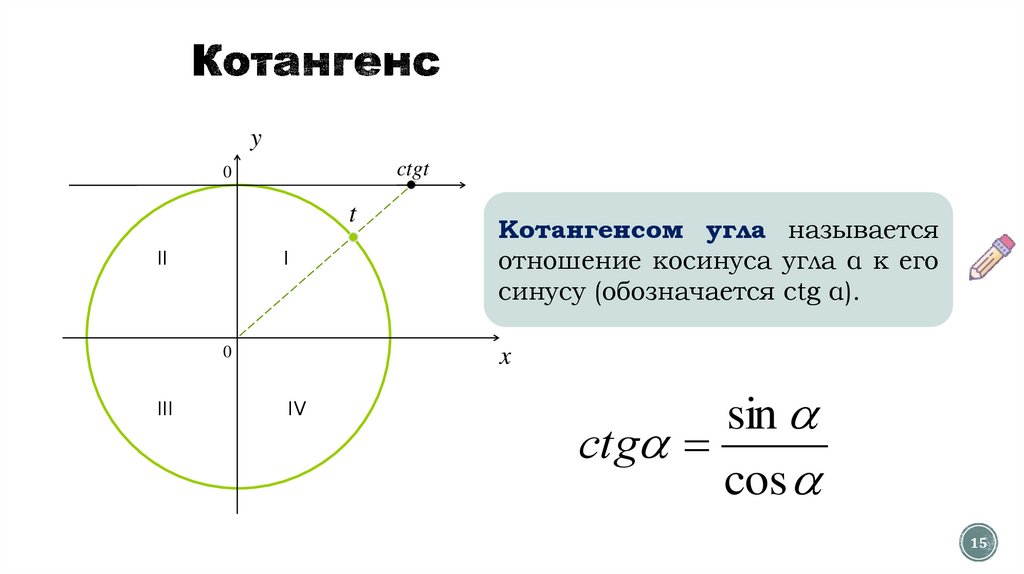
Котангенсом угла называется
отношение косинуса угла α к его
синусу (обозначается ctg α).
x
IV
sin
сtg
cos
15

16.

16

17.

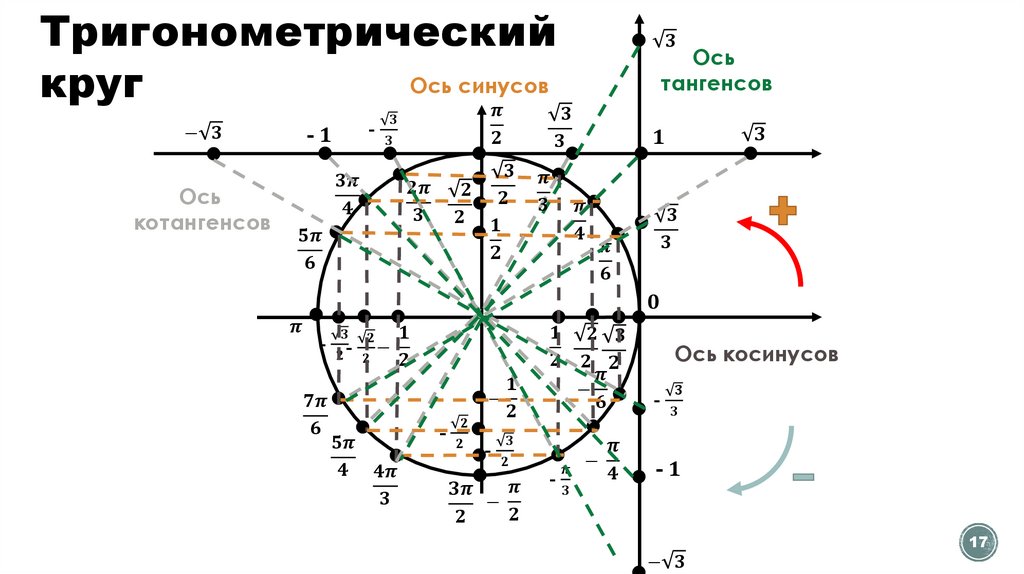
Тригонометрический
Ось синусов
круг