Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус, тангенс, котангенс угла

1.

Классификация углов из книги по альпинизму:
«Перпендикулярно» — 60 градусов;
«Мой дорогой сэр, абсолютно
перпендикулярно!» — 65 градусов;
«Нависающе»— 70 градусов.
Дж. Литтлвуд. «Математическая смесь».

2. Тема урока:

”Основные понятия тригонометрии:
радианная мера угла, вращательное
движение, синус, косинус, тангенс,
котангенс угла, основные
тригонометрические тождества,
формулы приведения”

3. Цели урока:

рассмотреть понятия радианной меры угла,
вращательного движения, синуса, косинуса,
тангенса, котангенса угла, основные
тригонометрические тождества, формулы
приведения
формировать умения применять
тригонометрические тождества, формулы
приведения

4.

1.Что такое
тригонометрия?
2.Для чего она мне
нужна?

5.

Во время равномерного
вращательного
движения тело
совершает движение по
окружности с
одинаковой скоростью,
но с изменяющимся
направлением. Например,
такое движение
совершают стрелки
часов по циферблату.

6.

Единица измерения величины угла называется градусом и
1
составляет
часть полного оборота.
360
В технике за единицу измерения принимают полный оборот.
А в мореплавании за единицу измерения углов принят румб,
1
равный
части полного оборота.
32

7.

Радиан – универсальная единица измерения дуг и углов.
Радианной мерой угла называется отношение
длины дуги окружности, заключенной между сторонами угла
и с центром в вершине угла, к радиусу этой окружности
Угол в 1 радиан – это такой центральный угол, длина дуги
которого равна радиусу окружности
180 радиан
0
n
0
n
180
радиан

8.

Синусом угла α называется
отношение ординаты точки В к R.
Косинусом угла α называется
отношение абсциссы точки В к R.
Тангенсом угла α называется
отношение ординаты точки В к ее
абсциссе.
Котангенсом угла α называется
отношение абсциссы точки В к ее
ординате.
y
B (x;y)
α
R
x

9. Основные формулы тригонометрии.

sin cos 1
2
2
cos
ctg
sin
sin
tg
cos
tg ctg 1
1
tg 1
cos 2
2
1
ctg 1
sin 2
2

10. Формулы сложения.

Основой для вывода всех остальных формул являются
формулы сложения:
cos cos cos sin sin
cos cos cos sin sin
sin sin cos cos sin
sin sin cos cos sin
tg tg
tg
1 tg tg
tg tg
tg
1 tg tg

11. Формулы приведения

Для преобразования выражений вида
n
n
n
n
sin , cos , tg , ctg
2
2
2
2
из формул сложения получим формулы приведения.

12. Мнемоническое правило

если 0
, то перед
2
приведенной функцией
ставится тот знак,
который имеет исходная
функция.
функция меняется на
«кофункцию», если n
нечетно; функция не
меняется, если n нечетно.

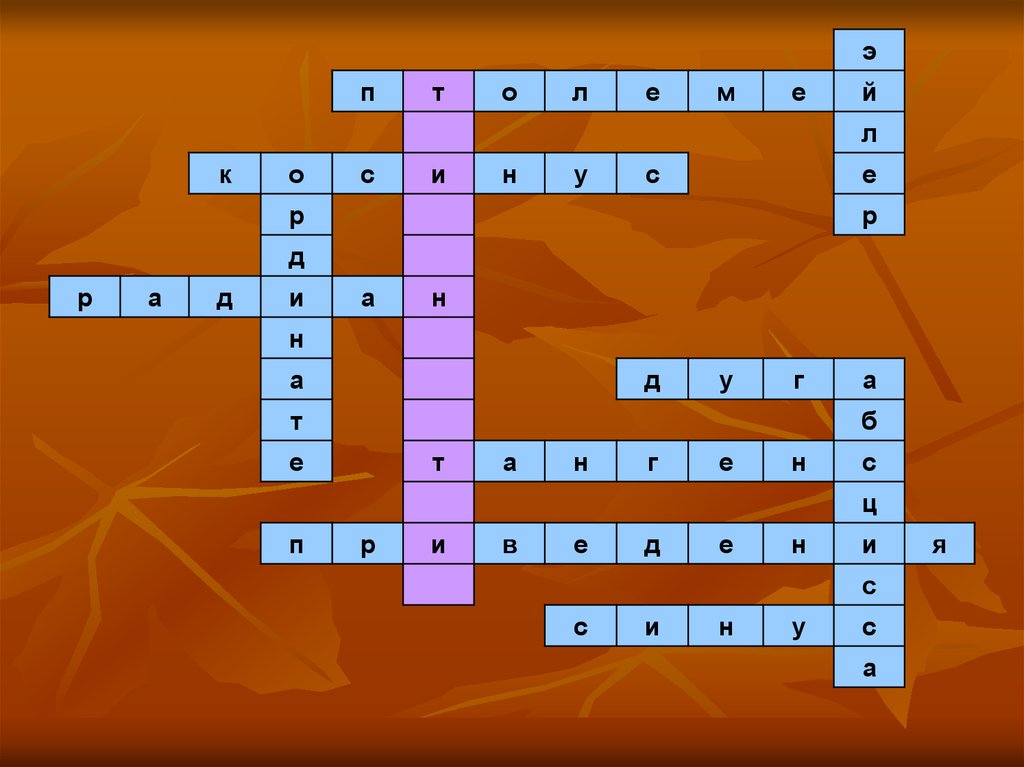
13. Проверка пройденного материала

14.

1
2
3
11
4
5
6
8
9
10
7

15.

э
2
й
л
3
4
е
р
5
6
8
9
10
7

16.

э
п
т
о
л
е
м
е
й
л
3
4
е
р
5
6
8
9
10
7

17.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
е
р
5
6
8
9
10
7

18.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
р
е
р
д
5
и
н
а
6
т
е
8
9
10
7

19.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
р
е
р
д
р
а
д
и
а
н
н
а
6
т
е
8
9
10
7

20.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
е
р
р
д
р
а
д
и
а
н
н
а
д
т
е
8
9
10
у
г
а

21.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
е
р
р
д
р
а
д
и
а
н
н
а
д
т
е
у
г
а
б
8
с
ц
9
и
с
10
с
е

22.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
е
р
р
д
р
а
д
и
а
н
н
а
д
у
г
т
е
а
б
т
а
н
г
е
н
с
ц
9
и
с
10
с
а

23.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
е
р
р
д
р
а
д
и
а
н
н
а
д
у
г
т
а
б
е
т
а
н
г
е
н
с
ц
п
р
и
в
е
д
е
н
и
с
10
а
я

24.

э
п
т
о
л
е
м
е
й
л
к
о
с
и
н
у
с
е
р
р
д
р
а
д
и
а
н
н
а
д
у
г
т
а
б
е
т
а
н
г
е
н
с
ц
п
р
и
в
е
д
е
н
и
с
с
и
н
у
с
а
я

25.

э
п
т
о
л
е
м
е
р
к
р
а
д
о
с
и
р
г
д
о
и
а
л
н
у
с
е
р
н
н
о
а
м
т
е
е
т
д
у
г
р
и
а
б
а
н
г
е
н
р
п
й
с
ц
в
е
д
е
н
я
и
с
с
и
н
у
с
е
я

26. Задание на дом:

А.Н. Колмогоров «Алгебра и начала анализа»
страница 5, пример 1 – законспектировать