Похожие презентации:
Основные моменты тригонометрии
1.
Тригонометрия-наше всё!!!!Подготовили
ученики 10В
класса:Бабкин
Артём,Потапов
Дмитрий,Окатье
в Дмитрий.
2.
Задача..Задачей нашего совместного проекта
является доступным языком объяснить
основные моменты тригонометрии.
.Рассказать как,и где применяется
тригонометрия.
3.
ЦельЦель нашего проекта привить любовь к
тригонометрии учащихся 10В класса!!!
4.
Тригонометрия▪ Тригонометрия-это часть геометрии,
где с помощью тригонометрических
функций связываются элементы
треугольника.
▪ Тригонометрия-это объект
математического анализа, где
тригонометрические уравнения
изучаются методами алгебры.
5.
Этапы развития тригонометрии▪ Тригонометрия в древности являлась
вспомогательным разделом астрономии.
Древнегреческие ученые разработали
«тригонометрию хорд».
▪ Древнеиндийские ученые заменили хорды
синусами.
▪ В VIII веке математики Востока превратили
тригонометрию в самостоятельную
математическую дисциплину. Ими были введены
другие тригонометрические функции и составлены
таблицы.
▪ Окончательный вид тригонометрия приобрела в
XVIII веке в трудах Л.Эйлера.
6.
Использованиетригонометрии в жизни.
.
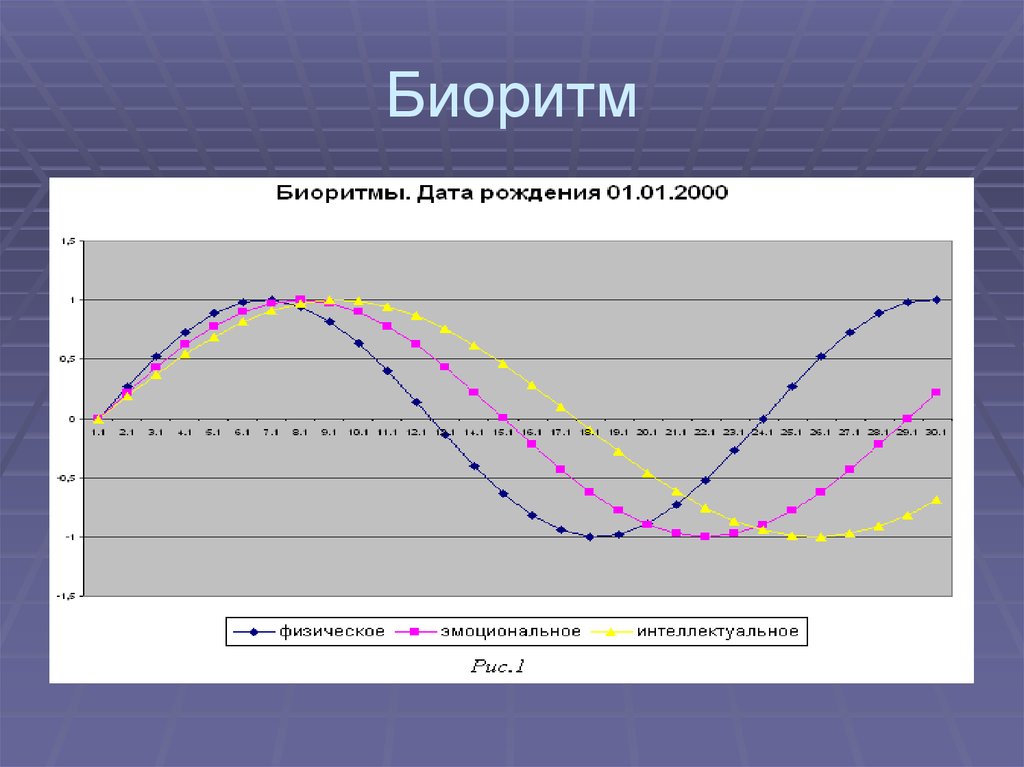
Модель биоритмов можно построить с
помощью тригонометрических функций.Для
построения модели биоритмов необходимо
ввести:дату рождения человека,дату
отсчета (день,месяц,год)и длительность
прогноза(кол-во дней).
.Используется в строительстве,а
особенно в архитектуре.
7.
Биоритм8.
В архитектуре.9.
Основные понятия✓тригонометрическая
✓градусы и радианы
✓синус и косинус
✓тангенс и котангенс
окружность
10.
yB
+
II
I
R=1
A
C
0
III
IV
D
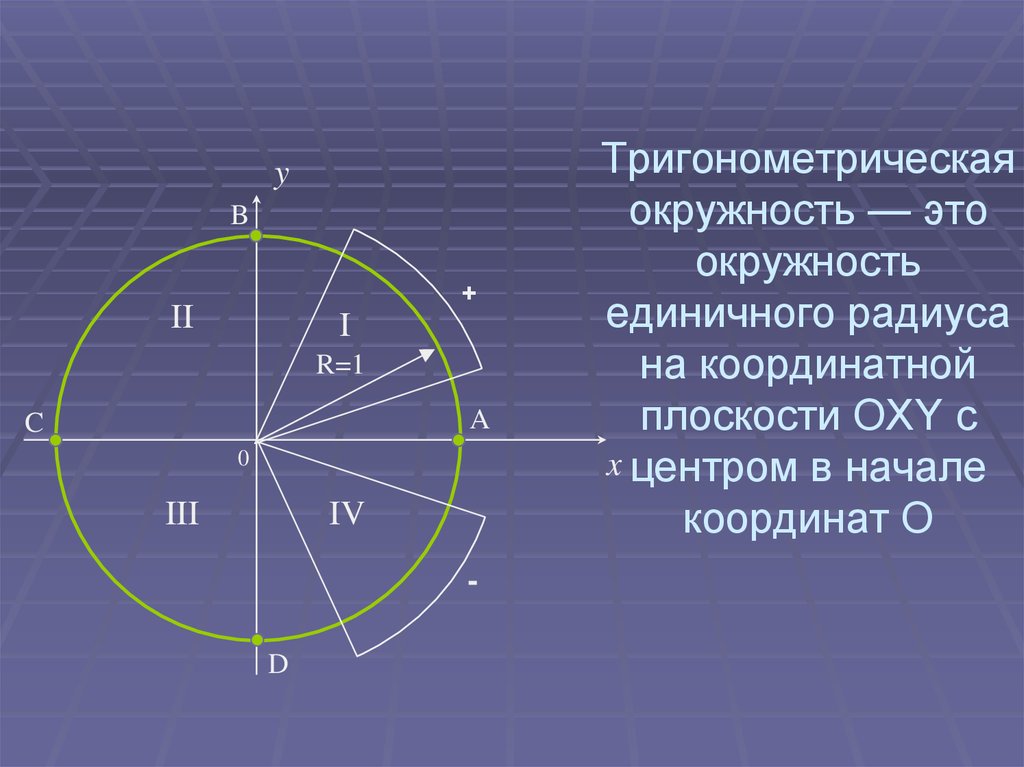
Тригонометрическая
окружность — это
окружность
единичного радиуса
на координатной
плоскости OXY с
x центром в начале
координат O
11.
Градусы и радианыy
+
x
0
12.
Градусы и радианыy
x
0
-
13.
yt
sint
0
cost
x
Косинус и
синус.
Xабцисасса
Y-ордината
14.
Тангенсy
t
I
II
-
+
0
+
III
tgt
IV
0
x
15.
Котангенсy
ctgt
0
t
II
I
-
+
0
+
-
III
IV
x
16.
Значения тригонометрическихфункций некоторых углов
t
0
п/6
п/4
п/3
п/2
tg t
0
√3/3
1
√3
-
ctg t
-
√3
1
√3/3
0
17.
Основные тригонометрическиетождества
▪
▪
▪
▪
▪
▪
sin2x+cos2x=1
tg t = sin t / cos t, где t≠ п/2+пк
ctg t = cos t / sin t , где t≠ пк
tg t ∙ ctg t = 1, где t≠ пк /2
1+tg2 t=1/cos2t, где t≠п/2+пк, к э Z
1+ctg2t=1/sin2t, где t≠ пк, к э Z
18.
Тригонометрические функцииуглового аргумента
▪ а0=па/1800 рад.
▪ 10=п/1800 рад.
▪ 1 рад=1800 /п
Угол в 1 радиан-это центральный угол,
опирающийся на дугу длиной 1, длина
которой равна радиусу окружности.
19.
✓cost = a✓sint = a
Уравнения
20.
Уравнение cost = a-1
t1
y
a
0
1. Проверить условие | a | ≤ 1
1
x
2. Отметить точку а на оси
абсцисс.
3. Построить перпендикуляр в
этой точке.
4. Отметить точки пересечения
перпендикуляра с окружностью.
5. Полученные точки – решение
уравнения cost = a.
6. Записать общее решение
уравнения.
-t1
21.
Частные случаи уравнения cost = acost = 1
π
y 2
cost = 0
π
-1
0
0
1
x
cost = -1
π
2
22.
РАБОТА У ДОСКИ1 ученик
1) sin x + sin y,
sin x - sin y
2) cos 85˚ + cos 35˚ - cos
25˚
2 ученик
1) cos x + cos y,
cos x - cos y
2) sin 20˚ + sin 40˚ - cos
10˚
23.
Запомнить,важно!!Основные понятия
✓тригонометрическая
✓градусы и радианы
✓синус и косинус
✓тангенс и котангенс
окружность
24.
Подведение итогов1)Чем занимались на уроке?
2)Что узнали нового на уроке?
3)Понравился ли вам урок?
4)Поставьте оценки в дневник.
25.
ВЫВОД:Таким образом,я
надеюсь,что мы хоть
чуть-чуть помогли вам
лучше понять эту не
простую тему!!
СПАСИБО ЗА ВНИМАНИЕ!!























 Математика
Математика