Похожие презентации:
Решение задач на применение признаков равенства треугольников
1.
2.
Теоретический опросКакую геометрическую фигуру изучаем?
Какие вы знаете виды треугольников?
Какие треугольники называются равными?
Что помогает определить равенство треугольников?
Какие признаки треугольников вы знаете?
3.
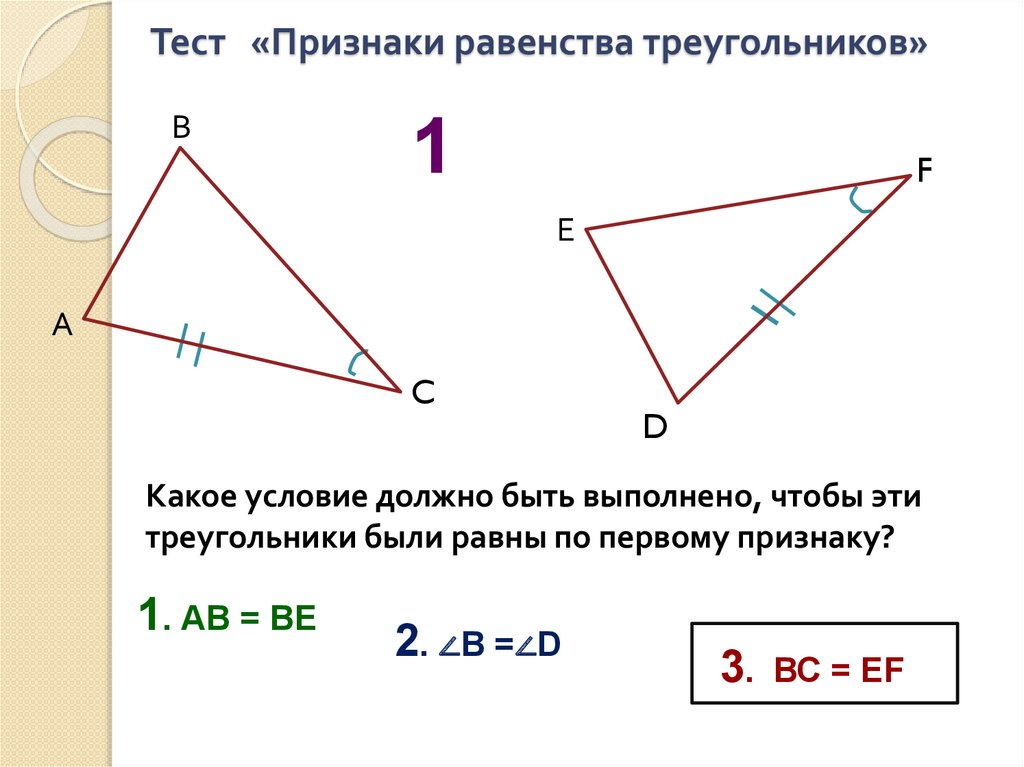
Тест «Признаки равенства треугольников»В
1
F
Е
А
C
D
Какое условие должно быть выполнено, чтобы эти
треугольники были равны по первому признаку?
1. АВ = ВЕ
2. ∠В =∠D
3.
ВС = ЕF
4.
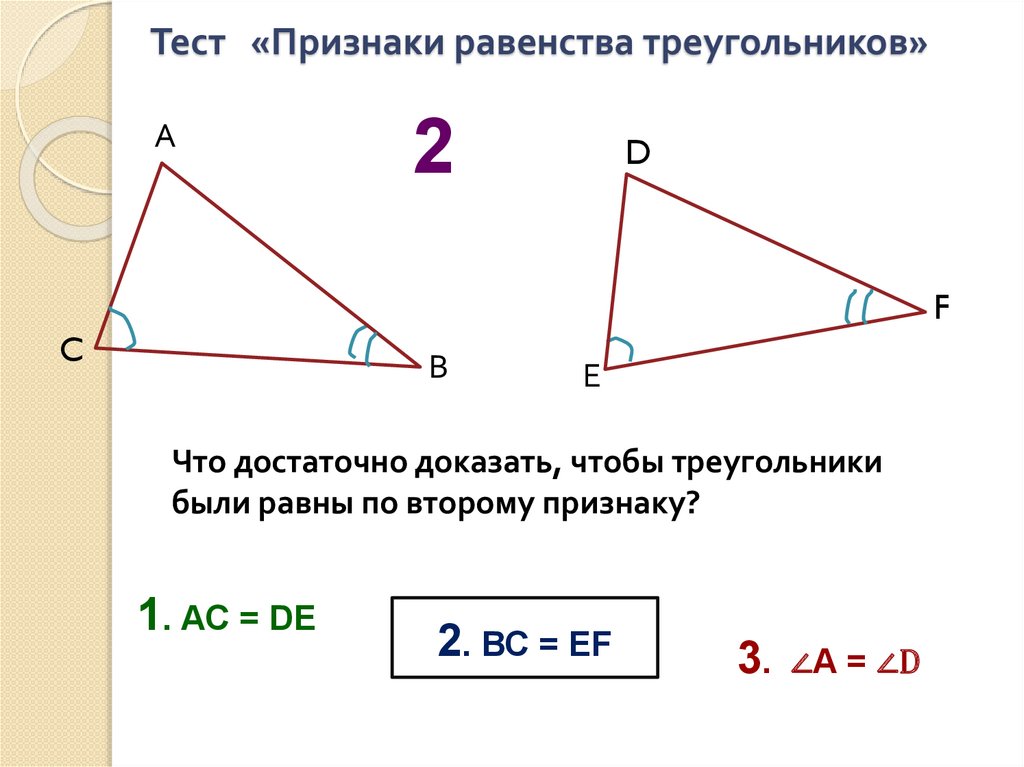
Тест «Признаки равенства треугольников»А
2
D
F
C
В
Е
Что достаточно доказать, чтобы треугольники
были равны по второму признаку?
1. АС = DЕ
2. ВС = ЕF
3.
∠А = ∠D
5.
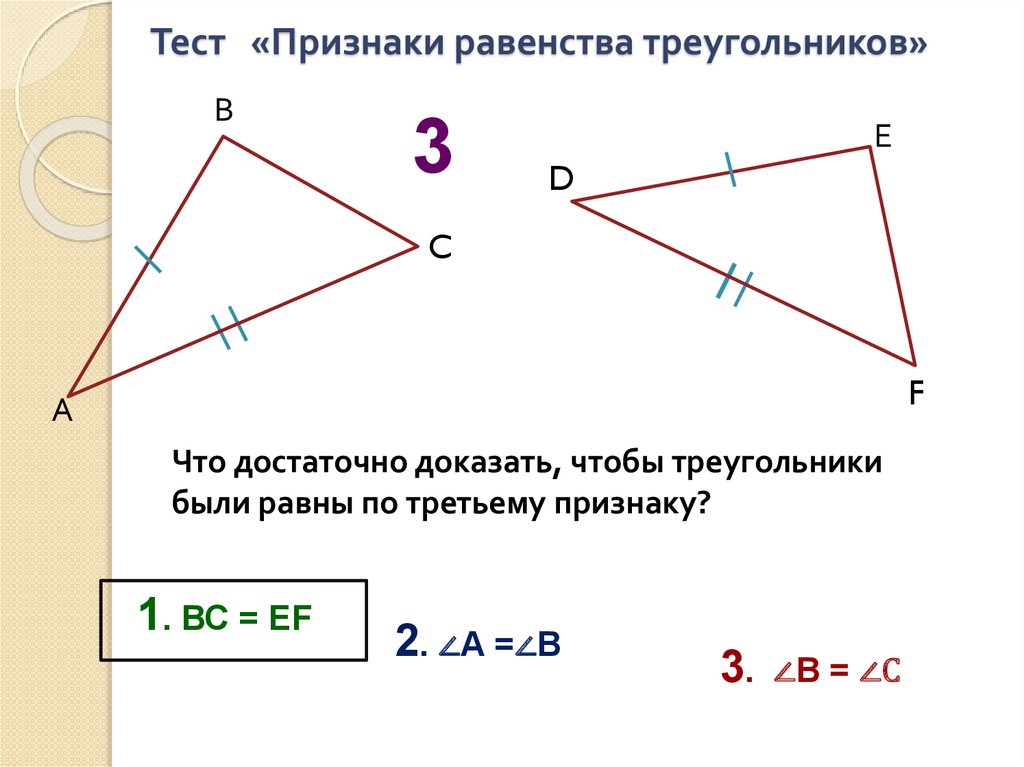
Тест «Признаки равенства треугольников»В
3
Е
D
C
F
А
Что достаточно доказать, чтобы треугольники
были равны по третьему признаку?
1. ВС = ЕF
2. ∠А =∠В
3.
∠В = ∠С
6.
Тест «Верно-неверно»№
п/п
Утверждение
+/ –
1
Если в треугольнике две стороны равны, то треугольник называется
равнобедренным.
2
Отрезок, соединяющий вершину треугольника с противоположной стороной,
называется медианой треугольника.
3
Если три стороны одного треугольника соответственно равны трем сторонам
другого треугольника, то такие треугольники равны.
4
Если сторона и два угла одного треугольника равны соответственно стороне и
двум углам другого треугольника, то такие треугольники равны.
+
–
+
–
5
Если две стороны и угол между ними одного треугольника соответственно
равны двум сторонам и углу между ними другого треугольника, то такие
треугольники равны.
+
6
В треугольнике углы при основании равны.
7
Биссектриса равнобедренного треугольника, проведенная к основанию,
является медианой и высотой.
8
Если три угла одного треугольника соответственно равны трем углам другого
треугольника, то такие треугольники равны.
–
+
–
7.
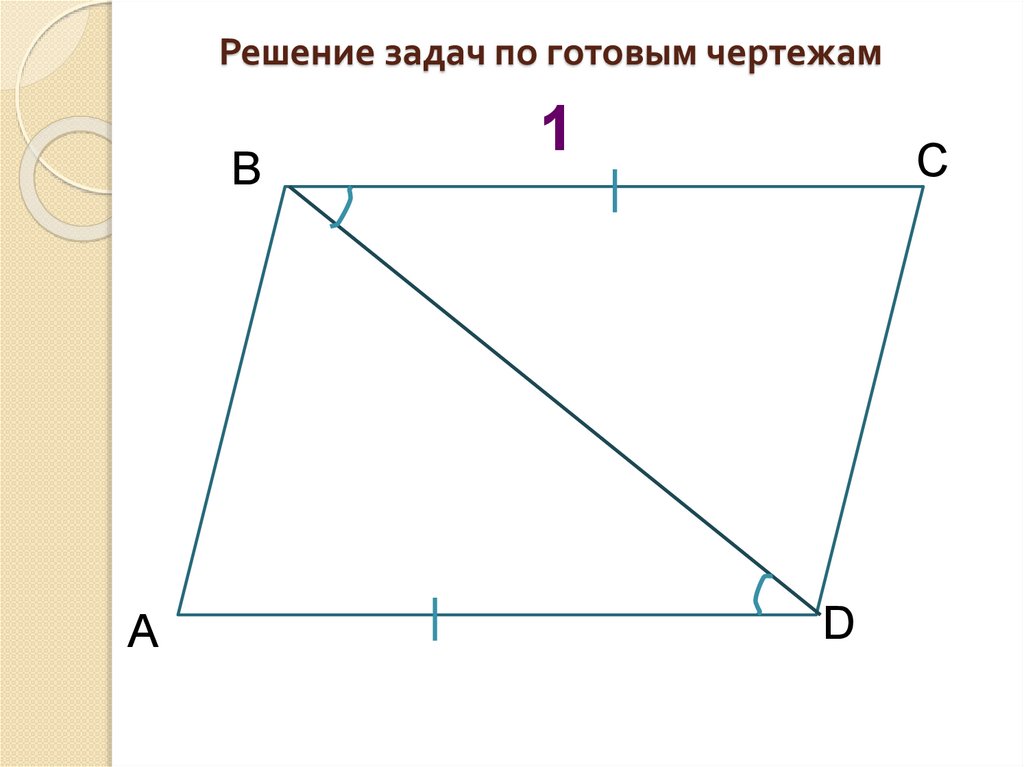
Решение задач по готовым чертежамВ
А
1
С
D
8.
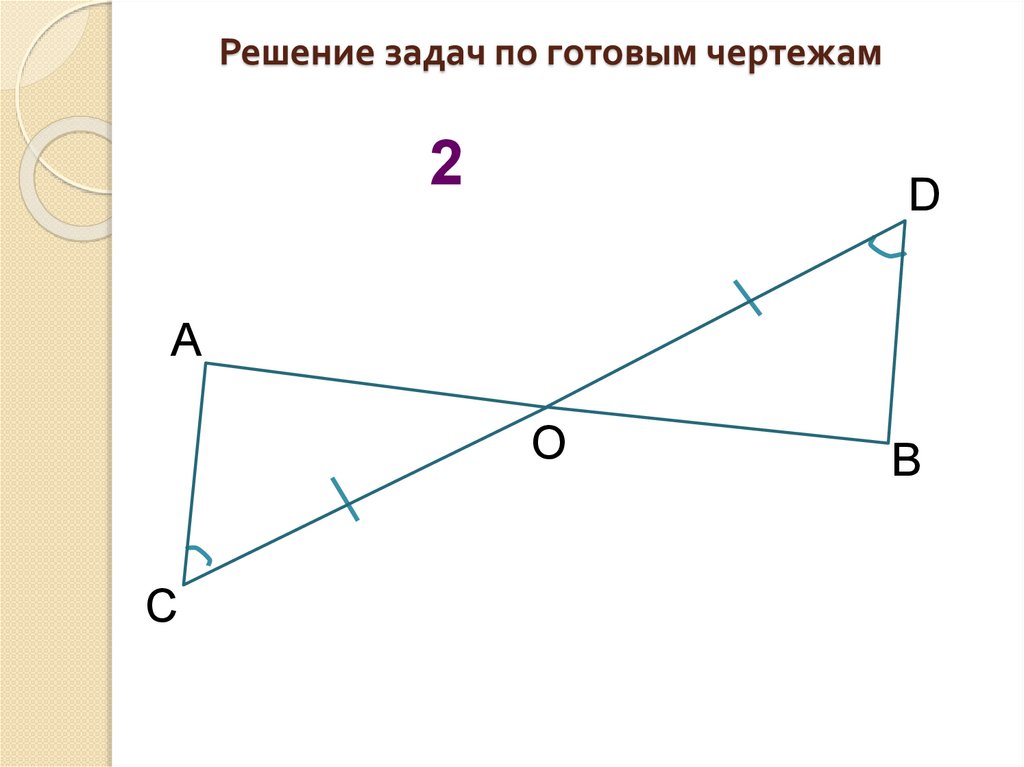
Решение задач по готовым чертежам2
D
А
О
С
В
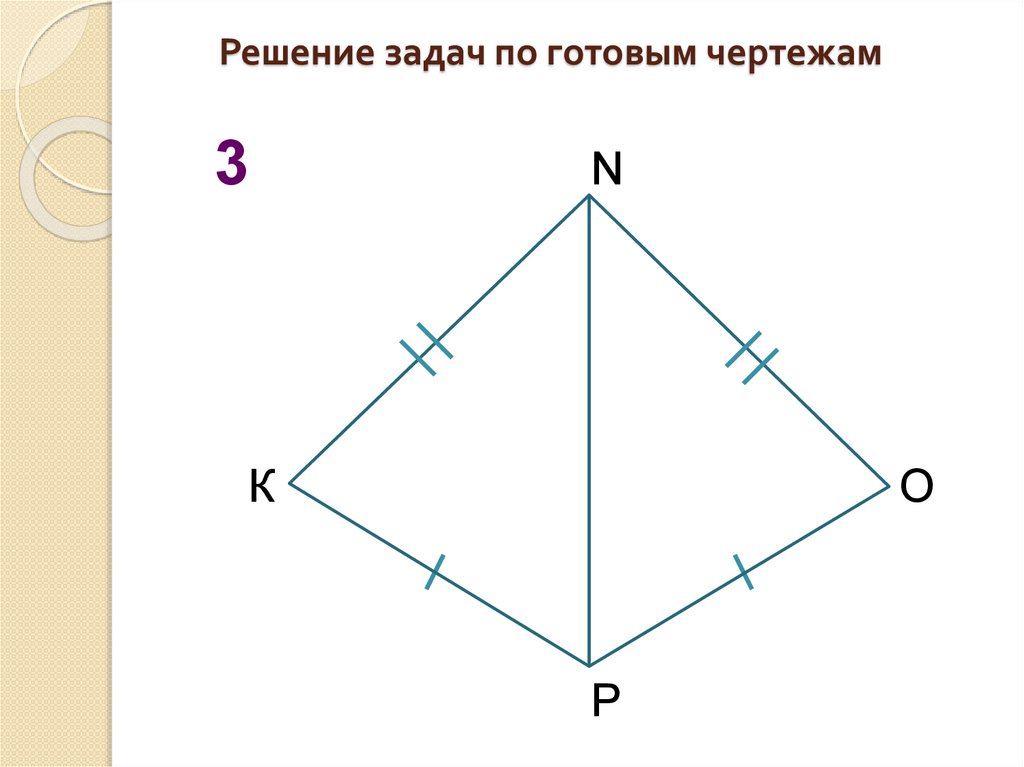
9.
Решение задач по готовым чертежам3
N
К
О
Р
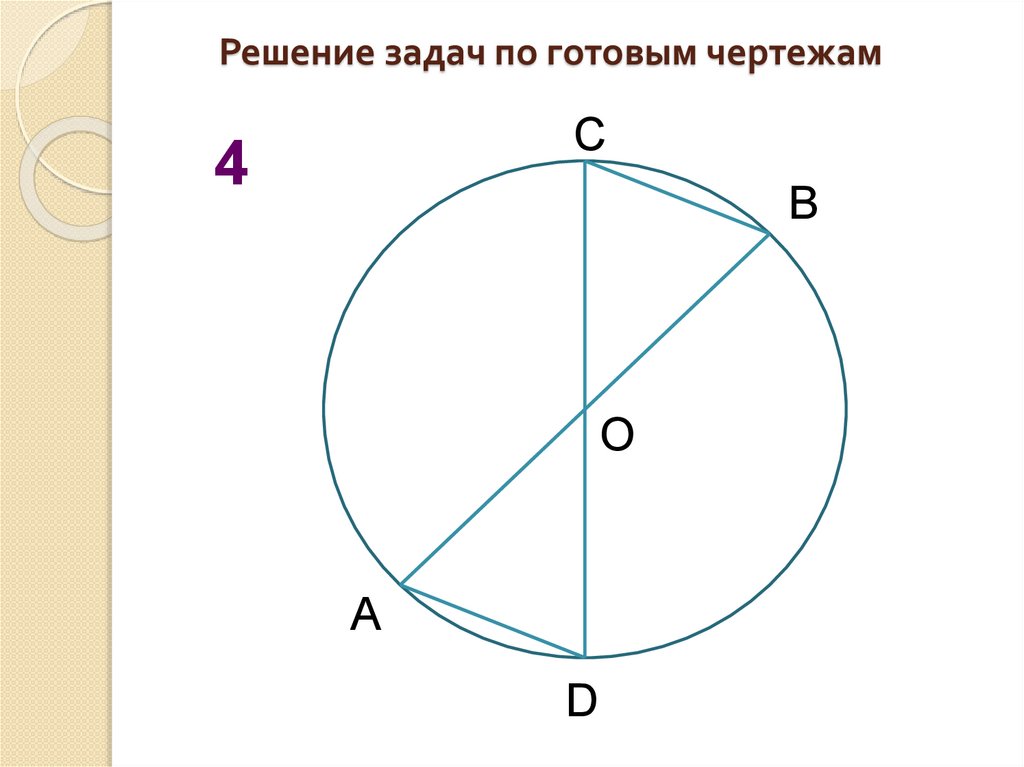
10.
Решение задач по готовым чертежамС
4
В
О
А
D
11.
Историческая справка12.
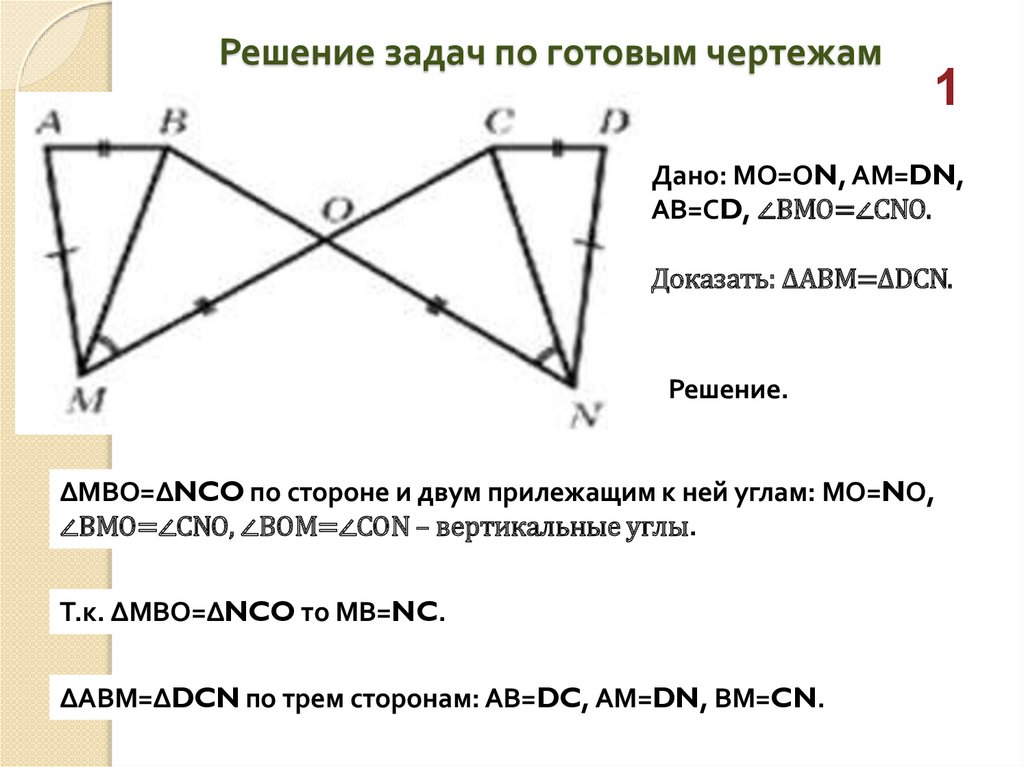
Решение задач по готовым чертежам1
Дано: МО=ОN, АМ=DN,
АВ=СD, ∠ВМО=∠СNО.
Доказать: ∆АВМ=∆DCN.
Решение.
∆МВО=∆NCO по стороне и двум прилежащим к ней углам: МО=NО,
∠ВМО=∠СNО, ∠ВОМ=∠СОN – вертикальные углы.
Т.к. ∆МВО=∆NCO то МВ=NC.
∆АВМ=∆DCN по трем сторонам: АВ=DC, АМ=DN, ВМ=CN.
13.
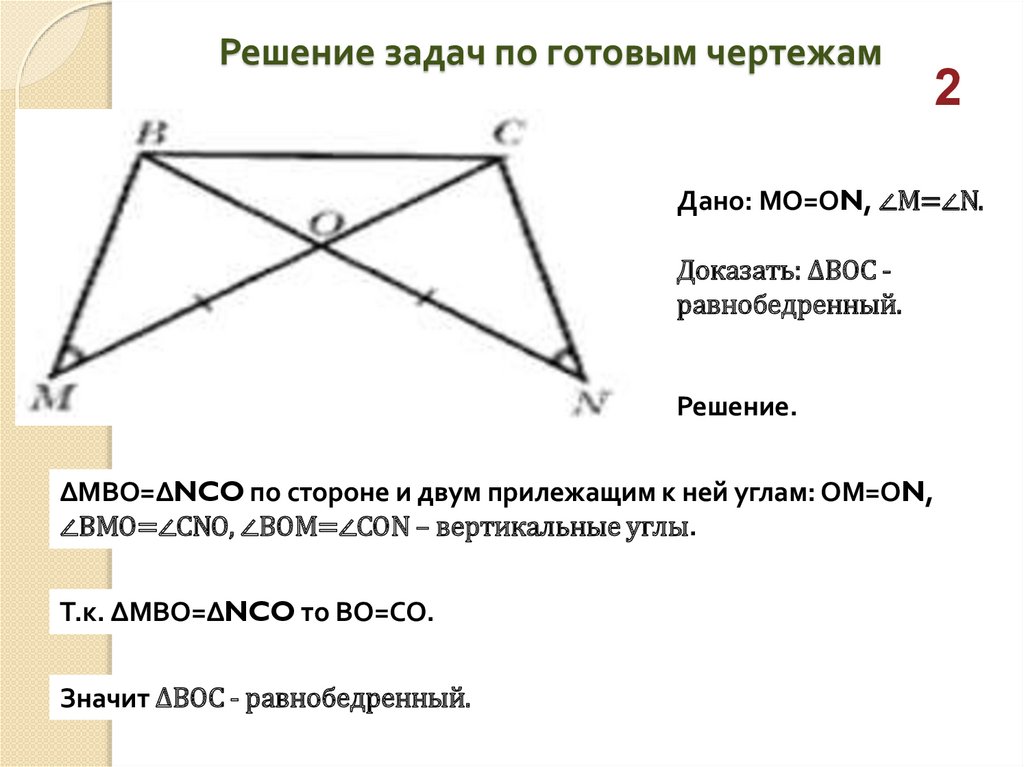
Решение задач по готовым чертежам2
Дано: МО=ОN, ∠М=∠N.
Доказать: ∆ВОС равнобедренный.
Решение.
∆МВО=∆NCO по стороне и двум прилежащим к ней углам: ОМ=ОN,
∠ВМО=∠СNО, ∠ВОМ=∠СОN – вертикальные углы.
Т.к. ∆МВО=∆NCO то ВО=СО.
Значит ∆ВОС - равнобедренный.
14.
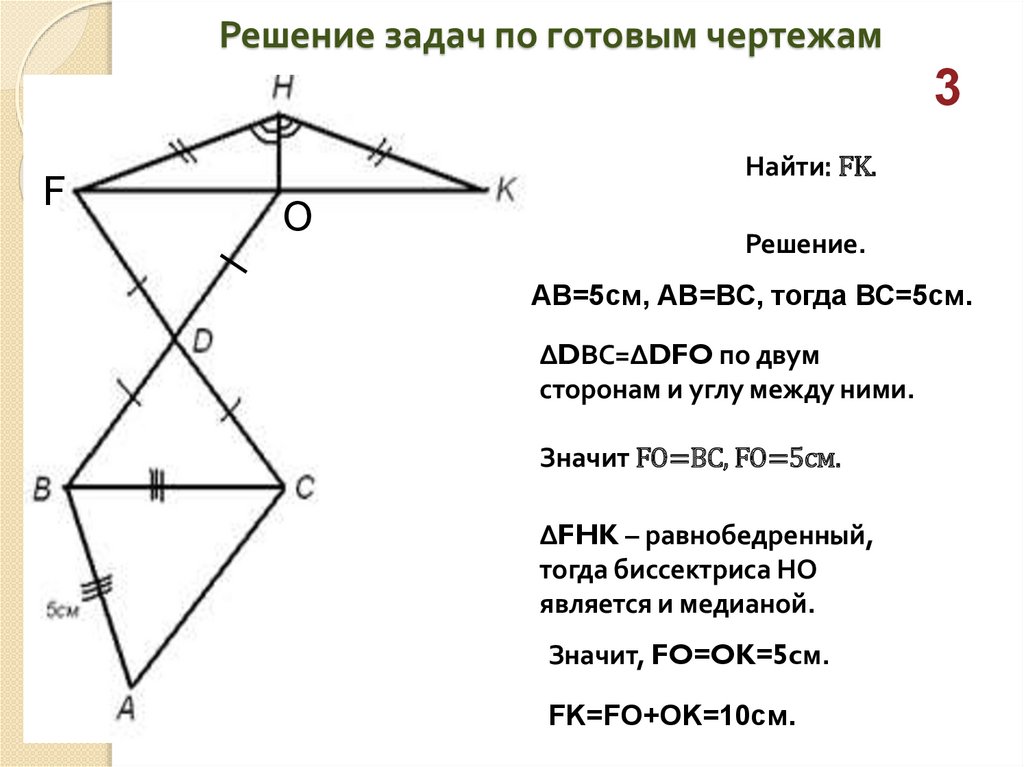
Решение задач по готовым чертежам3
F
Найти: FK.
О
Решение.
АВ=5см, АВ=ВС, тогда ВС=5см.
∆DВС=∆DFO по двум
сторонам и углу между ними.
Значит FO=ВС, FO=5см.
∆FHK – равнобедренный,
тогда биссектриса НО
является и медианой.
Значит, FO=OK=5cм.
FK=FO+OK=10см.
15.
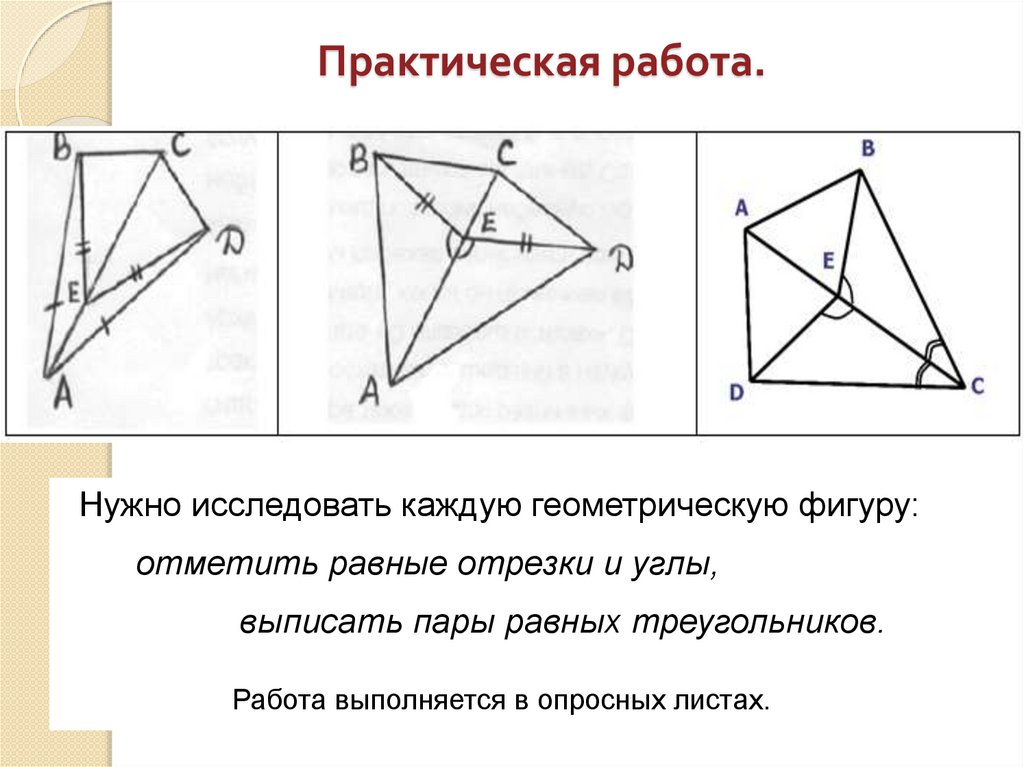
Практическая работа.Нужно исследовать каждую геометрическую фигуру:
отметить равные отрезки и углы,
выписать пары равных треугольников.
Работа выполняется в опросных листах.
16.
Задание на домОтветить на вопросы к главе 2 (стр. 47);
№140, №141.





 Математика
Математика








