Похожие презентации:
Определение определённого интеграла (Лекция 2)
1. ЛЕКЦИЯ 2
1.2.
3.
4.
Определение определенного интеграла
Свойства определенного интеграла
Формула Ньютона-Лейбница
Несобственные интегралы
2. Определение определённого интеграла
ОПРЕДЕЛЕНИЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
3. Обозначения и терминология
y f (x)[ a, b]
f ( x) 0
[ a, b]
a x0 x1 xn b
x [a, b]
4. Геометрическая иллюстрация
5. Определение интегральной суммы
y f (x)[ a, b]
6. Определение определенного интеграла
y f (x)[ a, b]
7. Обозначение определенного интеграла
y f (x)[ a, b]
f ( x)dx
f (x)
8. Замечания к определению определенного интеграла
9. Кусочно-непрерывные функции
10. Теорема о существовании определенного интеграла
y f (x)[ a, b]
b
f ( x)dx
a
y f (x)
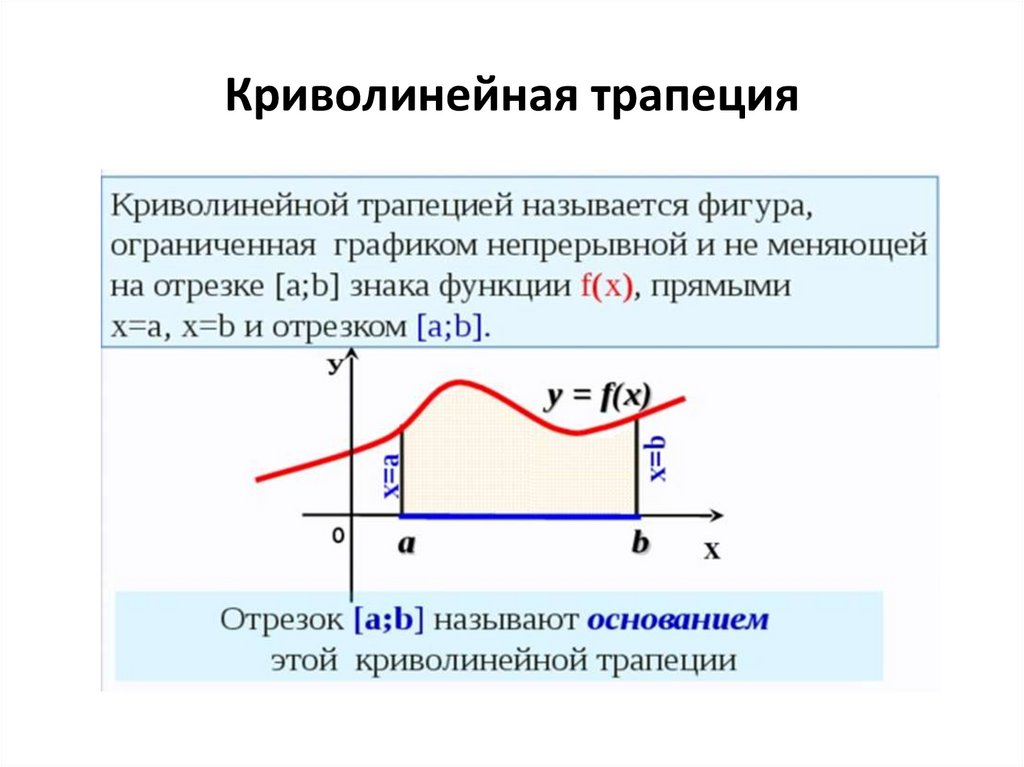
11. Криволинейная трапеция
12. Геометрический смысл определенного интеграла
13.
14. Свойства определенного интеграла
СВОЙСТВА ОПРЕДЕЛЕННОГОИНТЕГРАЛА
15.
16.
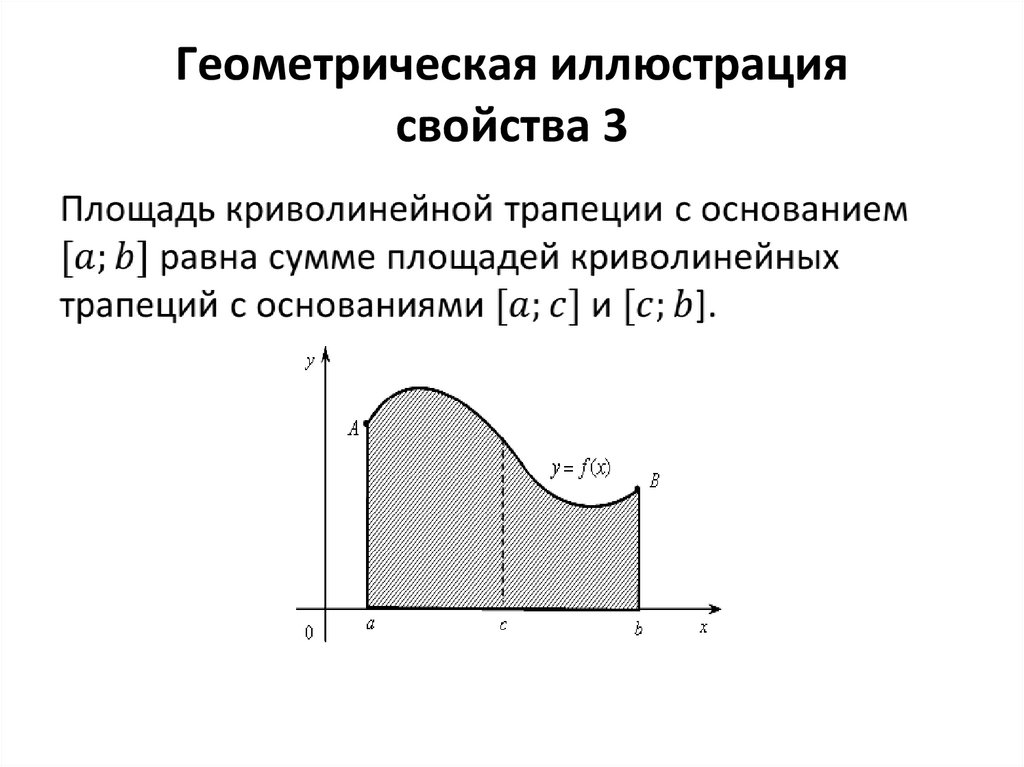
17. Геометрическая иллюстрация свойства 3
18.
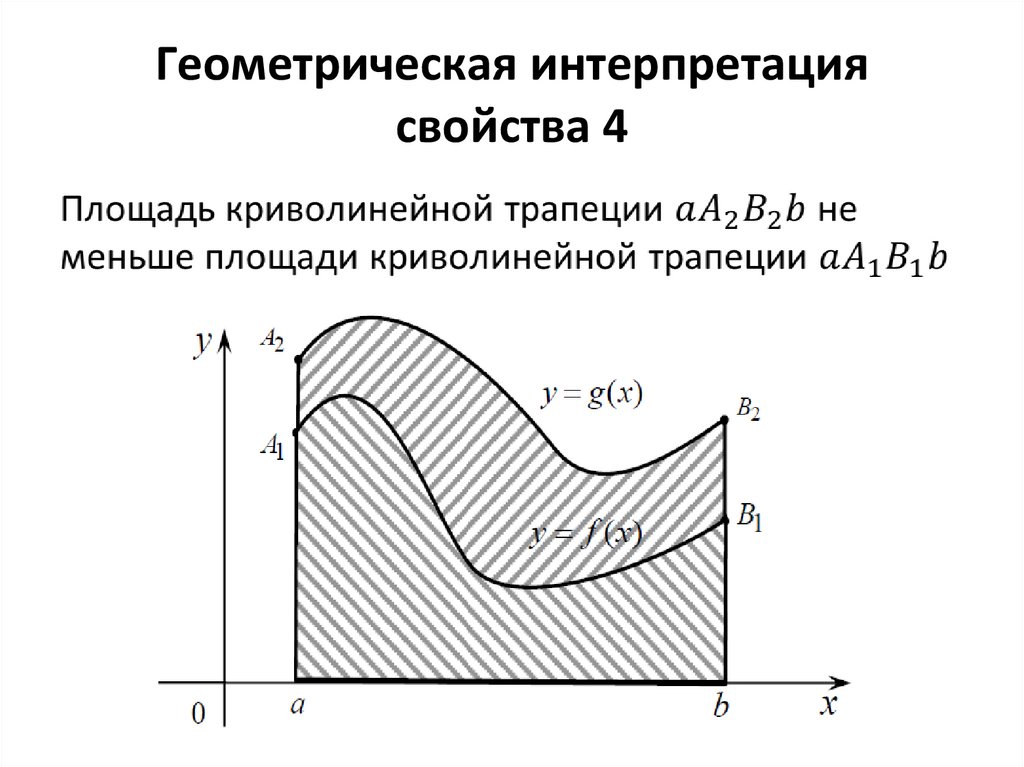
19. Геометрическая интерпретация свойства 4
20. Следствия из свойства 4
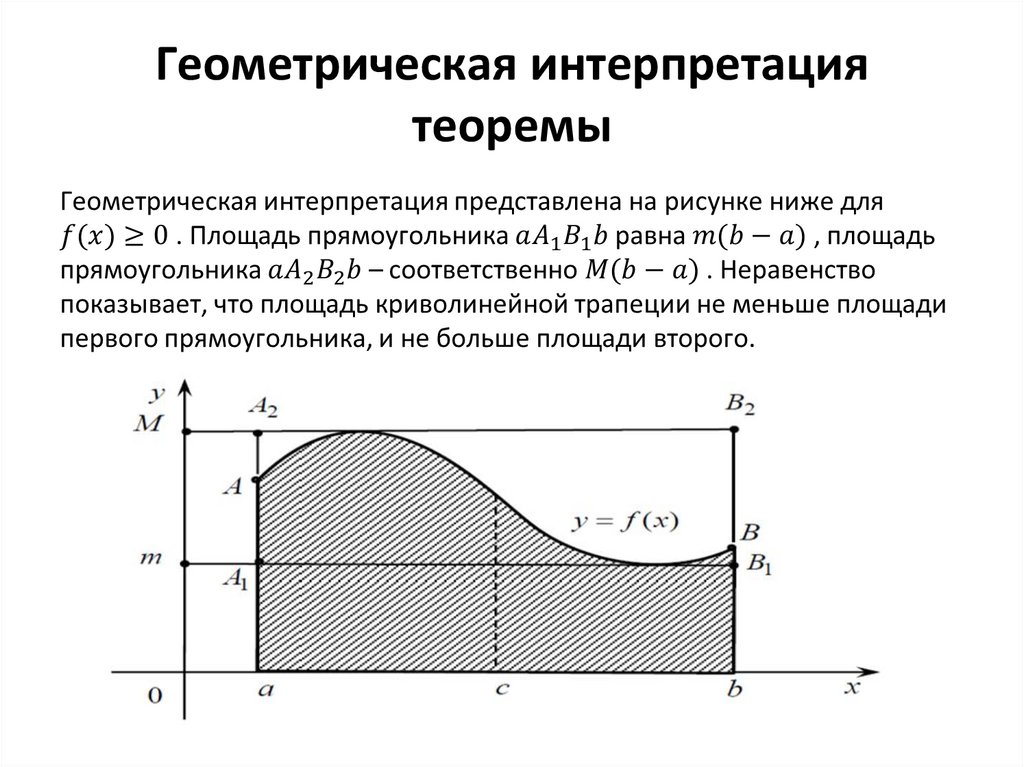
21. Теорема об оценке определенного интеграла
22. Геометрическая интерпретация теоремы
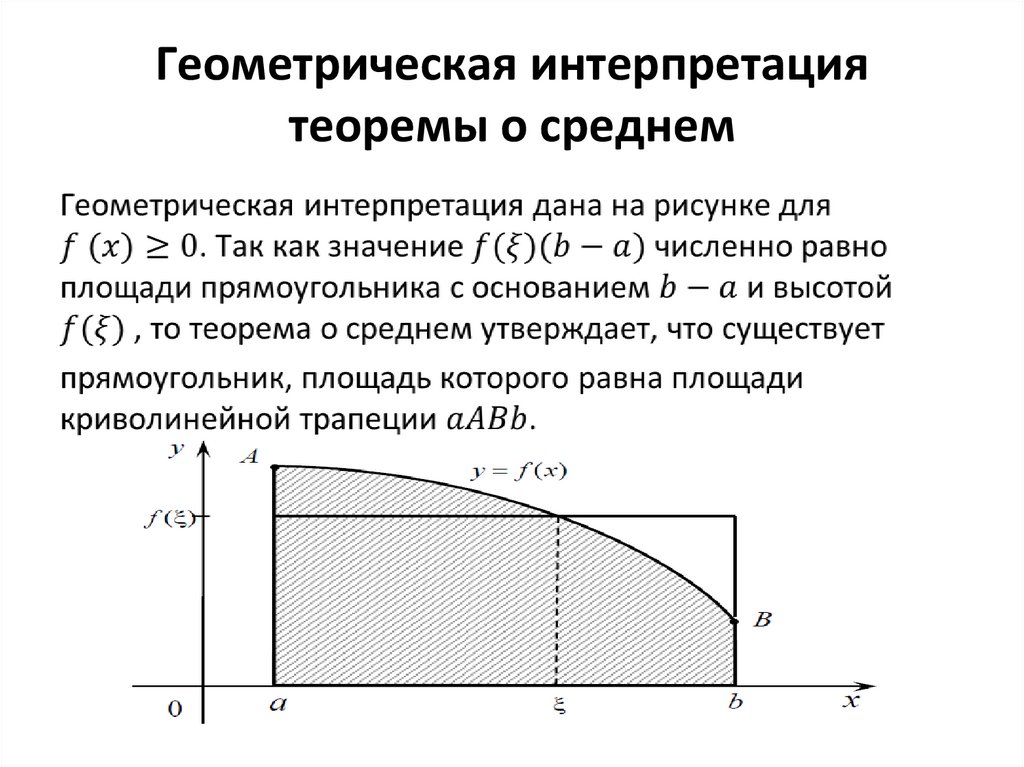
23. Теорема о среднем
24.
25. Геометрическая интерпретация теоремы о среднем
26.
27. Формула ньютона-лейбница
ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА28. Интегралы с верхним переменным пределом
y f (x)[ a, b]
x
F ( x) f (t )dt
a
[ a, b]
29. Теорема о производной интеграла с верхним переменным пределом (теорема Берроу)
30. Доказательство
31.
32.
33. Замечание
34. Формула Ньютона - Лейбница
35. Доказательство
36.
x aa
f ( x)dx 0 F (a) C
a
x
C F (a)
f ( x)dx F ( x) F (a)
a
b
x b
f ( x)dx F (b) F (a)
a
37. Значение формулы Ньютона - Лейбница
Значение формулы Ньютона ЛейбницаФормула Ньютона – Лейбница – это одна из
немногих формул, объединяющих различные
разделы математики воедино. Если бы не было
формулы Ньютона – Лейбница, то неопределенные
интегралы не нашли бы приложения, а
определенные интегралы нельзя было бы
вычислить аналитически. Именно эта формула
делает интегральное исчисление важнейшим
инструментом для математического моделирования
процессов.
38. Ньютон и Лейбниц – гении науки
Исаак Ньютон(4.01.1643-31.03.1727)
Готфрид Вильгельм
Лейбниц
(1.07.1646-14.11.1716)
39. Методы вычисления определенного интеграла
МЕТОДЫ ВЫЧИСЛЕНИЯОПРЕДЕЛЕННОГО ИНТЕГРАЛА
40. Интегрирование по частям
Для вычисления определенного интегралаиспользуются формулы интегрирования по частям
и замены переменной. Эти формулы похожи на
соответствующие формулы для неопределенного
интегрирования, но имеют свою специфику.
Формула для интегрирования по частям:
b
udv
a
b
uv a
b
vdu
a
41. Интегрирование подстановкой
Замена переменной:b
a
f ( x)dx f ( (t )) (t )dt
где x (t ) - монотонная, непрерывно
дифференцируемая функция новой
переменной t на отрезке t ,
a ( ) , b ( ) .
42. Примеры
1)4
dx
6 cos
2)
3)
2
x
4
tgx 6
3
tg ( 4) tg ( 6) 1
3
32 4
(2 x 1)
2 x 1dx
2 3 2
0
4
0
93 1
1 26
9
3
3
3 3
x
1
u
x
;
dv
e
dx
x
x 1
xe
e x dx
xe dx
0 0
0
du dx; v e x
e 2
1
x 1
1
e e
2e 1
0
e
1
43. Примеры
4)dx
1
21
ln x t ; dt ; x 1 t 0
t
1
dx
tdt
x
0
2
2
1 x
0
x
e
t
1
e ln x
44. Несобственные интегралы
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ45. Определение несобственных интегралов
Несобственными называют интегралы сбесконечными пределами интегрирования
и/или интегралы от неограниченных функций.
b
Обозначение: f ( x)dx ,
, f ( x)dx
a
f ( x)dx
Для вычисления несобственных интегралов
формула Ньютона–Лейбница не применима.
46. Вычисление несобственных интегралов 1-го рода (с бесконечными пределами интегрирования)
bf ( x)dx lim f ( x)dx
b a
a
b
b
f ( x)dx lim f ( x)dx
a a
c
c
f ( x)dx f ( x)dx f ( x)dx
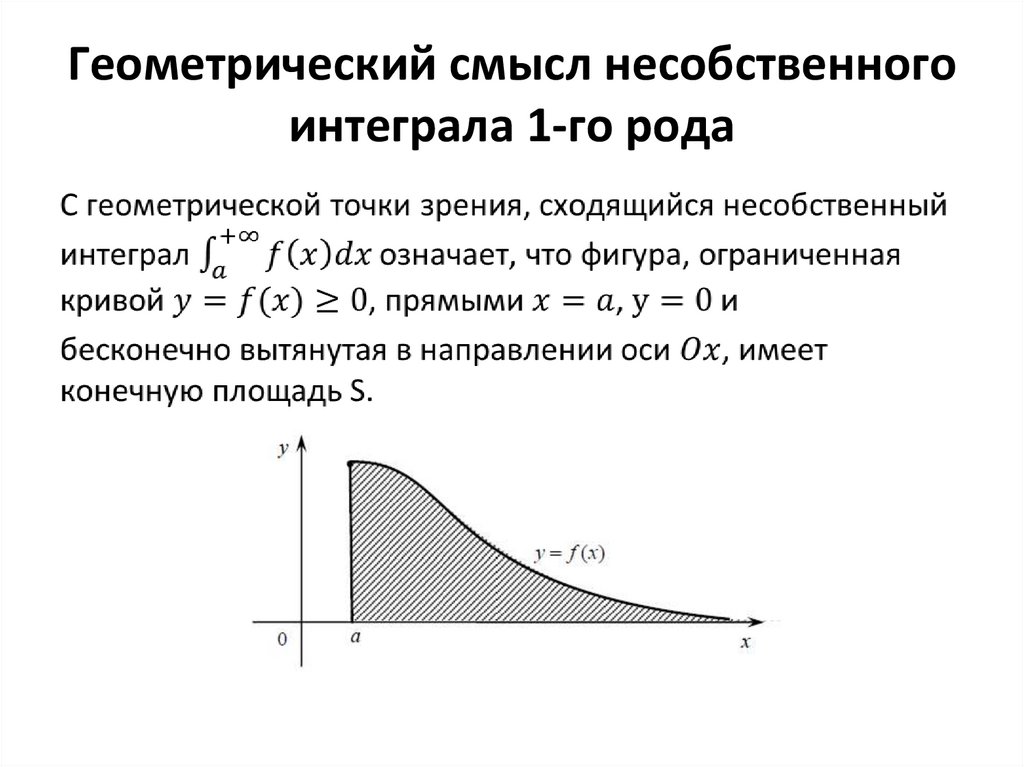
Если эти пределы существуют и конечны, то
соответствующий несобственный интеграл
называется сходящимся, если же - не существует
или бесконечен, то несобственный интеграл
называется расходящимся.
47. Геометрический смысл несобственного интеграла 1-го рода
48. Пример 1
49. Пример 2
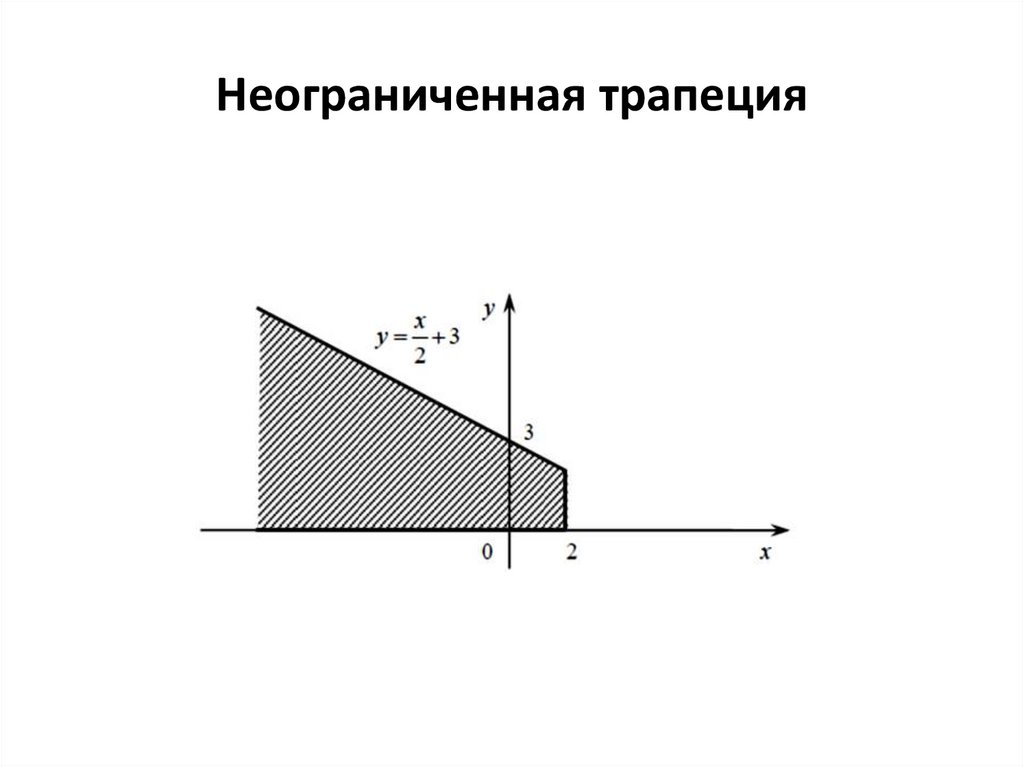
50. Неограниченная трапеция
51. Важный пример
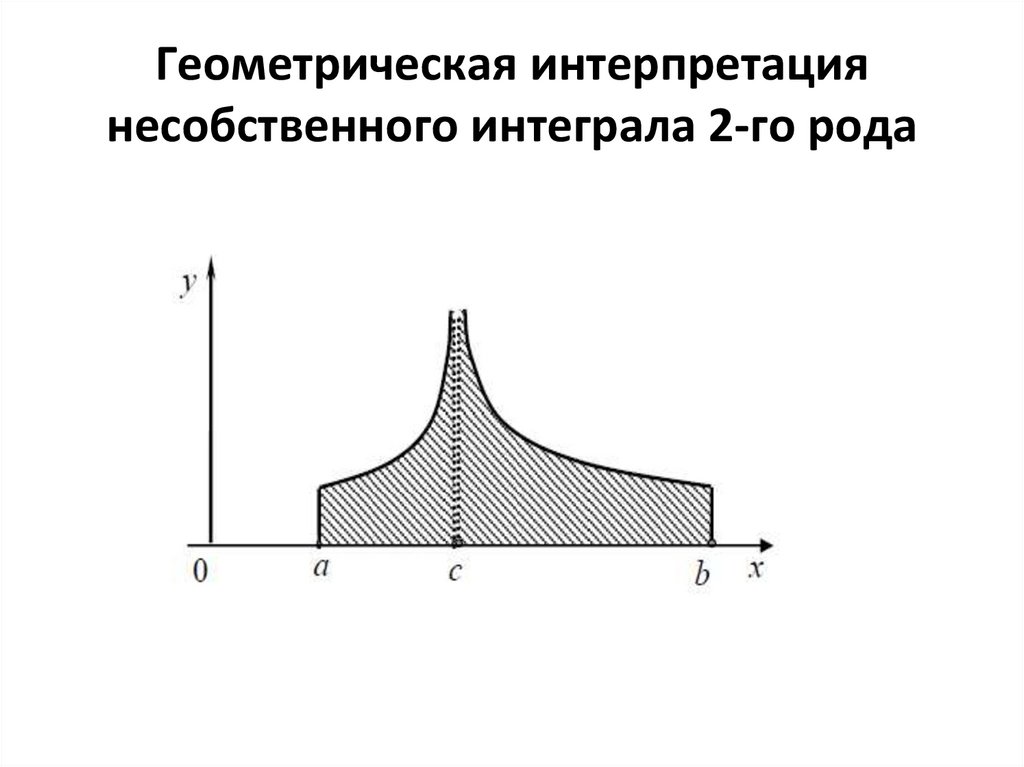
52. Вычисление несобственных интегралов 2-го рода (от неограниченных функций)
Пусть функция f (x) имеет бесконечныйодносторонний предел в какой-либо точке
c [a, b] , то по определению принимаем, что
несобственный интеграл 2-го рода от f (x)
на отрезке [a, b] равен
b
c
b
f ( x)dx lim f ( x)dx lim f ( x)dx
a
0 a
0 c
53. Геометрическая интерпретация несобственного интеграла 2-го рода
54. Частные случаи
ЕслиЕсли
b
b
lim f ( x) , то f ( x)dx lim f ( x)dx
x a 0
lim f ( x)
x b 0
a
b
0 a
b
f ( x)dx
, то f ( x)dx lim
0
a
b
a
lim f ( x)
Несобственный интеграл f ( x)dx , где x
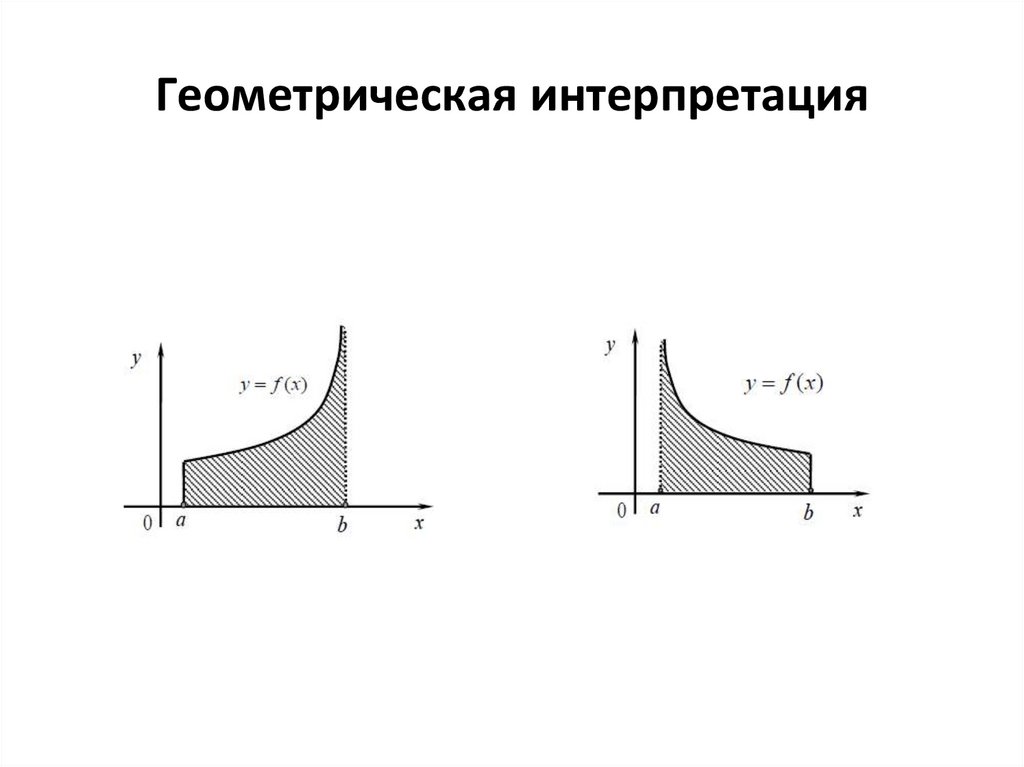
c 0
a
lim f ( x)
или x
для некоторого c [a, b] ,
c 0
называется сходящимся, если существуют оба
предела в определении интеграла, и расходящимся,
если не существует хотя бы один из них.
55. Геометрическая интерпретация
56. Пример вычисления несобственного интеграла 2-го рода
57. Ошибочное вычисление
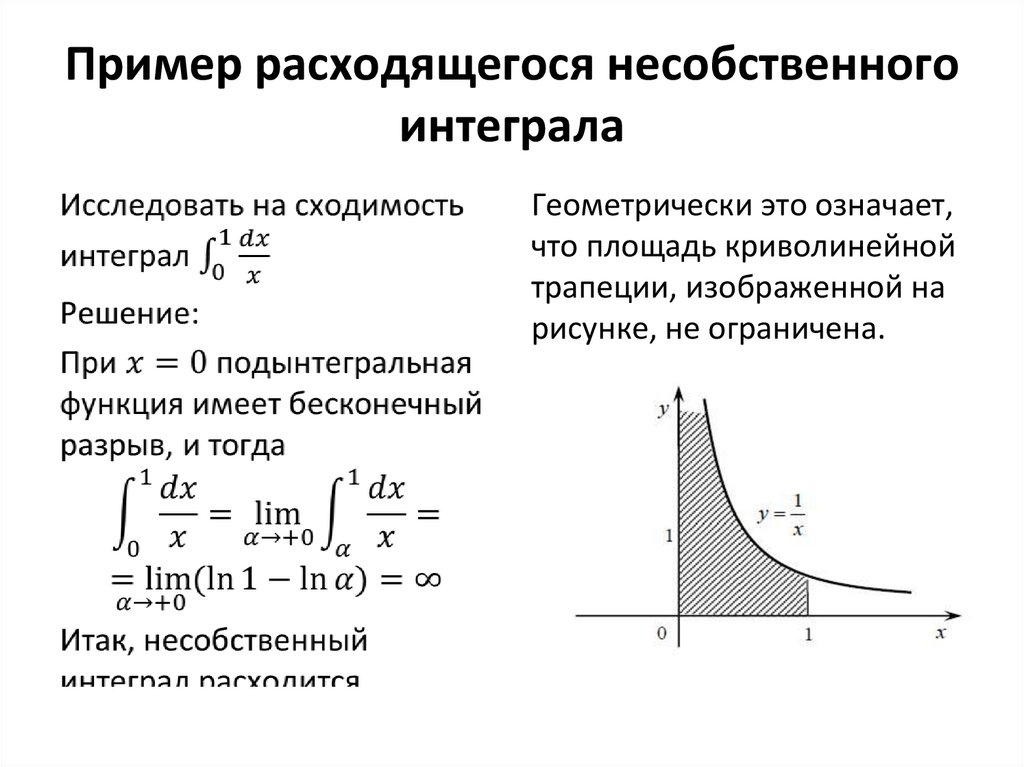
58. Пример расходящегося несобственного интеграла
Геометрически это означает,что площадь криволинейной
трапеции, изображенной на
рисунке, не ограничена.
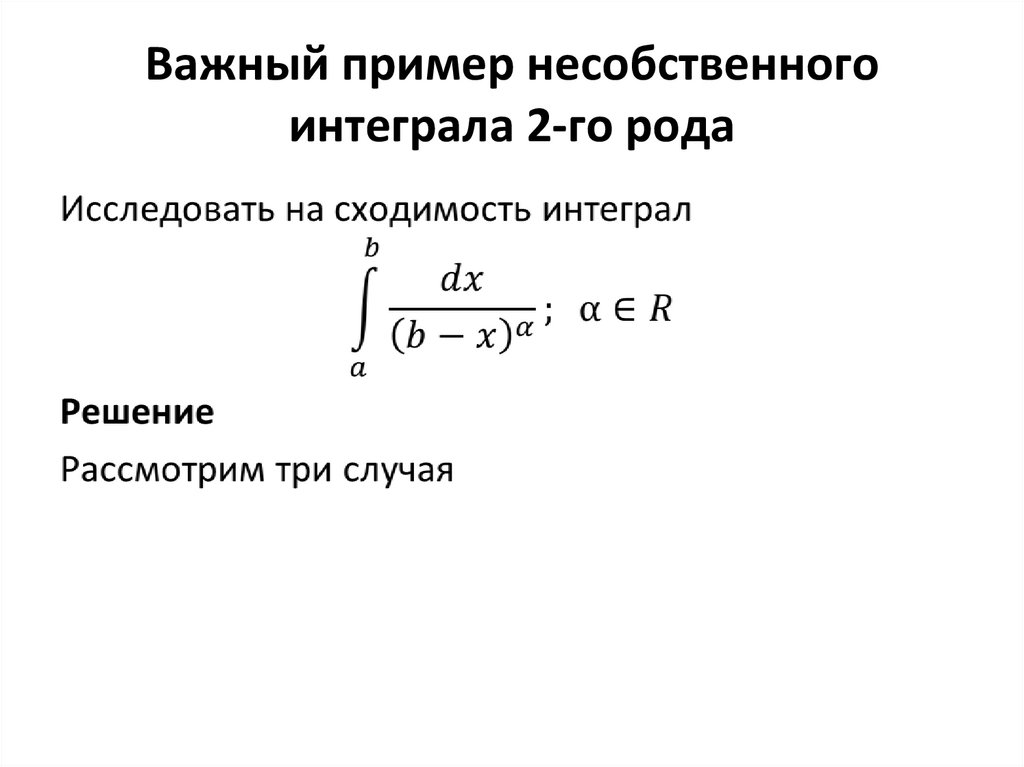
59. Важный пример несобственного интеграла 2-го рода
60. α=1
61. α>1
62. α<1
63. Примеры
1)2)
3)
4)
b
dx
b
1
1
lim
lim
lim
(
1
) 1
2
2
b 1 x
b x 1
b
b
1 x
c
dx
1
x
dx
2
dx
1
x
2
c
dx
1 x
2
2
2
1
1 dx
1
dx
lim
lim
2
x
lim 2(1 ) 2
0
0 x 0 x 0
1 dx
1x
2
0 dx
1x
2
1 dx
0x
2
dx
lim
0 1x
2
1 dx
lim
0 x
2



















































 Математика
Математика








