Похожие презентации:
Descompunerea valorilor singulare. Formularea problemei (curs 7)
1.
METODE NUMERICE – curs 7Cap. 5 Descompunerea valorilor singulare
5.1 Formularea problemei
A m n
p min{m, n}
r - rangul matricii A r p
r p - matrice deficientă de rang
r p - matrice de rang complet
Teoremă:
~
~
Oricare ar fi matricea A m n , există două matrici ortogonale U m m şi V n n ,
astfel încât:
~
~
~
~
sau A U V T ,
(1)
UT A V
unde este o matrice pseudo-diagonală, elementele nenule ale acesteia satisfăcând relaţia:
diag{ 1 , , p }, 1 2 p 0 .
1 , , p
m n
- valori singulare ale matricii A
- formă canonică diagonală a matricii A
relaţia (1) – descompunerea valorilor singulare
(2)
2.
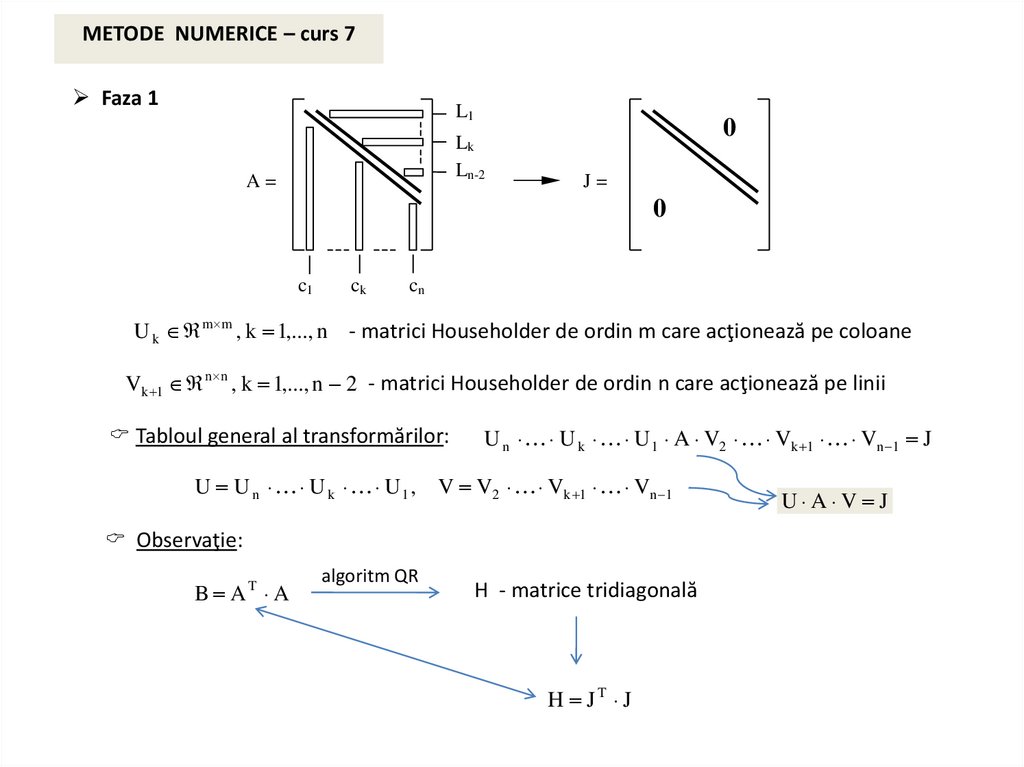
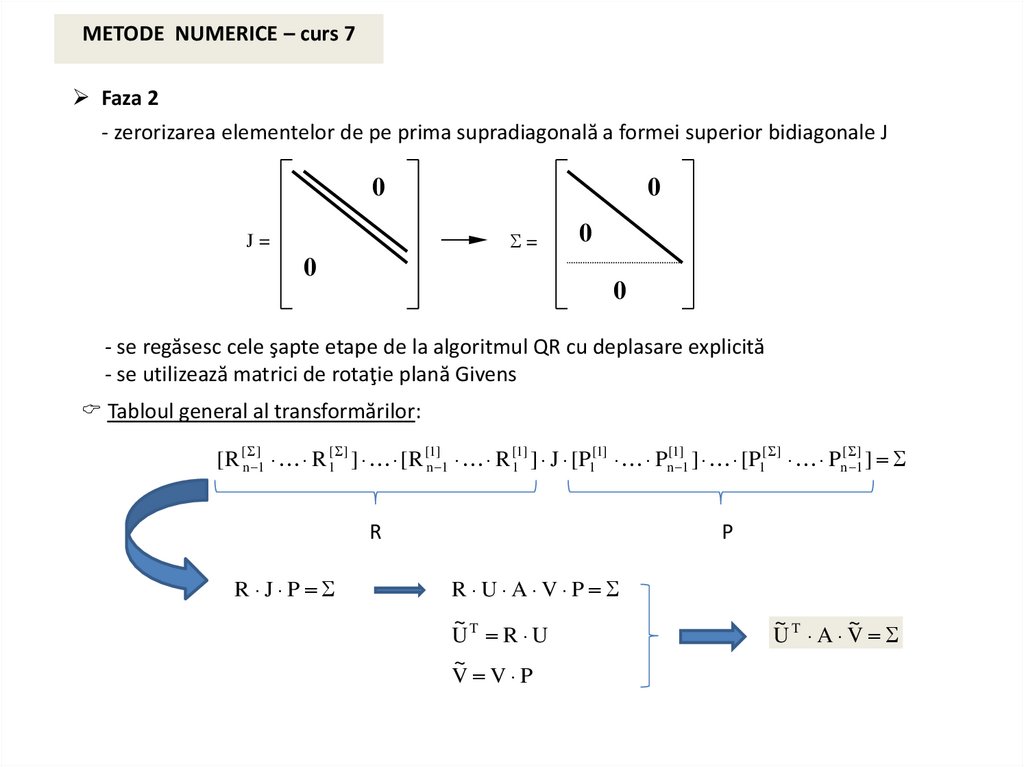
METODE NUMERICE – curs 7Demonstraţia teoremei algoritmul de descompunere a valorilor singulare
Observaţie:
- orice matrice este ortogonal echivalentă bilateral cu o matrice (pseudo)diagonală
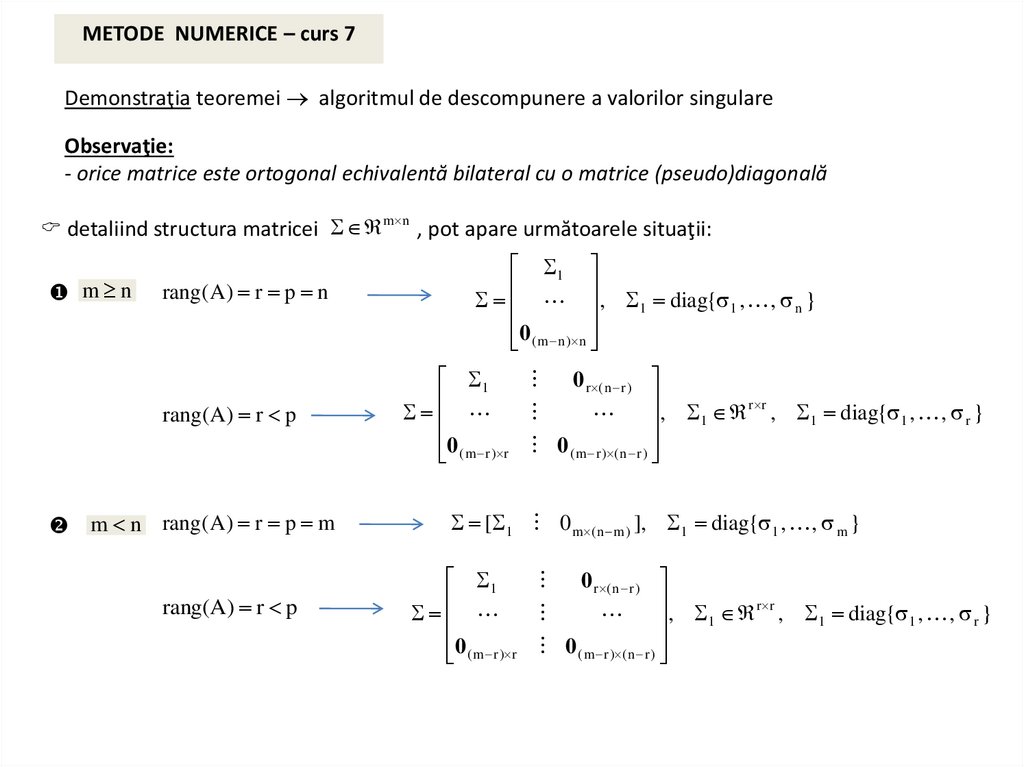
detaliind structura matricei m n , pot apare următoarele situaţii:
m n
rang(A) r p n
rang(A) r p
m n rang(A) r p m
rang(A) r p
1
, 1 diag{ 1 , , n }
0 ( m n ) n
1
0 ( m r ) r
0 r ( n r )
r r
, 1 , 1 diag{ 1 , , r }
0 ( m r ) ( n r )
[ 1 0 m ( n m ) ], 1 diag{ 1 , , m }
1
0 ( m r ) r
0 r ( n r )
r r
, 1 , 1 diag{ 1 , , r }
0 ( m r ) ( n r )
3.
METODE NUMERICE – curs 71 2 r 0, r 1 p 0
rangul matricei A este egal cu rangul matricei , care este egal cu r
rangul acestor matrici este egal cu numărul valorilor singulare nenule
~ ~
relaţia (1) poate fi scrisă sub forma: A V U
~
~v
- vectorii coloană ai V
i
~
~
u i - vectorii coloană ai U
T
T
A ~
v i i ~
ui ~
u i A i ~
vi
i 1,..., p
Definiţie:
~
Coloanele matricei V se numesc vectori singulari la dreapta ai matricei A, iar coloanele
~
matricei U se numesc vectori singulari la stânga ai matricei A.
4.
METODE NUMERICE – curs 7,
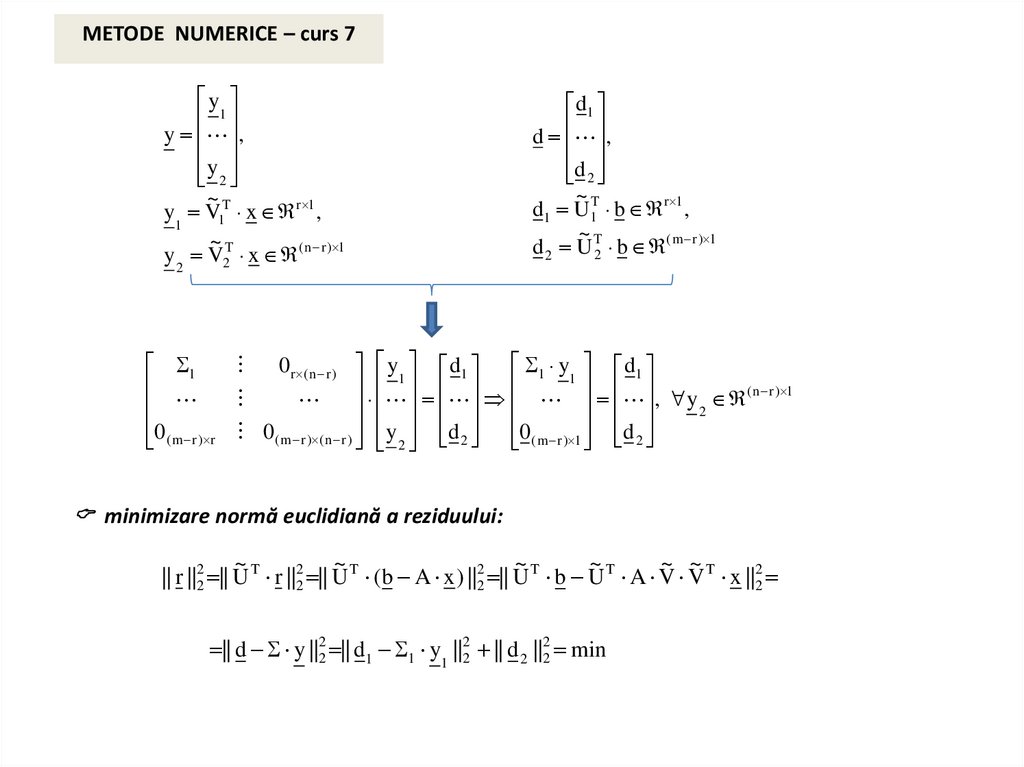
proprietăţi ale decompunerii valorilor singulare:
P1. valorile singulare ale matricei A sunt egale cu rădăcina pătratică pozitivă a valorilor
proprii ale matricei A T A :
i (A) i (A T A) , i 1,..., n
P2. dacă A n n este o matrice simetrică şi pozitiv semidefinită, atunci valorile proprii ale
matricei A sunt reale, pozitive, iar valorile singulare ale matricei A sunt egale cu valorile ei
proprii:
i (A) i (A), i 1,..., n
~
~
P3. scriind matricile U şi V sub forma:
~
~
~
U [~
u1 ~
ur ~
u r 1 ~
u m ] [U1 U 2 ]
~
~
~
V [~
v1 ~
vr ~
v r 1 ~
v n ] [V1 V2 ]
~
~
~
A U V T [U1
1
~
U2 ]
0 ( m r ) r
~
0 r ( n r ) V1T
~
0 ( m r ) ( n r ) V2T












 Математика
Математика








