Похожие презентации:
Понятие многогранника. Призма
1.
Понятиемногогранника. Призма.
2.
Определение: Поверхность составленнуюиз многоугольников и ограничивающую
некоторое геометрическое тело
называется многогранником.
Например: тетраэдр, параллелепипед
3.
Они имеют вершины, ребра, грани,диагонали
Определение: Отрезок соединяющий две
вершины не принадлежащие одной грани
называют диагональю многогранника.
Многогранники бывают выпуклые и
невыпуклые.
Параллелепипед и тетраэдр относятся к
выпуклым многогранникам
4.
Определение: Многогранник называютвыпуклым, если он расположен по одну
сторону от плоскости каждой его грани.
невыпуклый
α
5.
αвыпуклый
6.
В выпуклом многограннике сумма всехплоских углов при каждой ее вершине
меньше 360
+ + 360
7.
ПризмаЕвклид
определяет призму как
телесную фигуру,
заключенную между
двумя равными и
параллельными
плоскостями
(основаниями) и с
боковыми гранями
параллелограммами.
(III в до н.э.)
8.
Призмы вокруг нас9.
Определение: Многогранник составленныйиз двух равных многоугольников
расположенных в параллельных
плоскостях и n- параллелограммов
называется призмой.
Эти параллельные многоугольники
называются основаниями, а
параллелограммы боковыми гранями
Боковые ребра у призм равны
10.
Bnβ
B1
B2
h
Аn
А1
α
А2
Многогранник
А1А2..АnB1B2..Bnпризма.
А1А2..Аn и В1В2..Вnоснования призмы,
параллелограммы
А1А2В2В1 и др.-боковые
грани,
отрезки А1В1,А2В2,..АnВnбоковые ребра призмы,
перпендикуляр h- высота
призмы.
11.
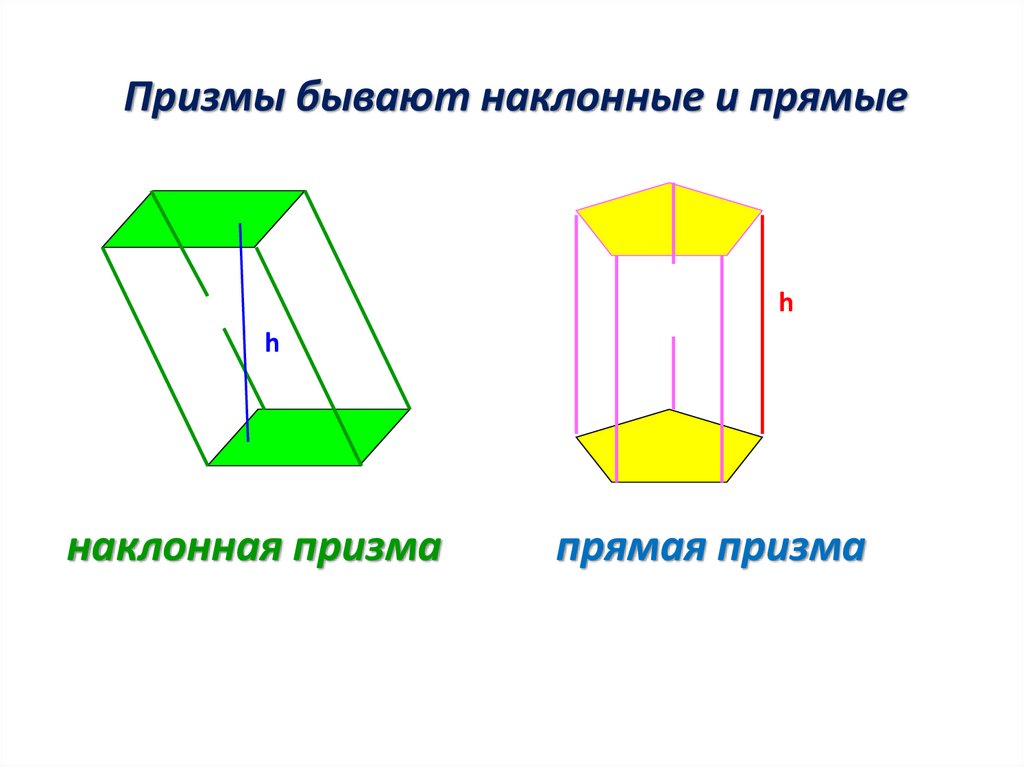
Призмы бывают наклонные и прямыеh
h
наклонная призма
прямая призма
12.
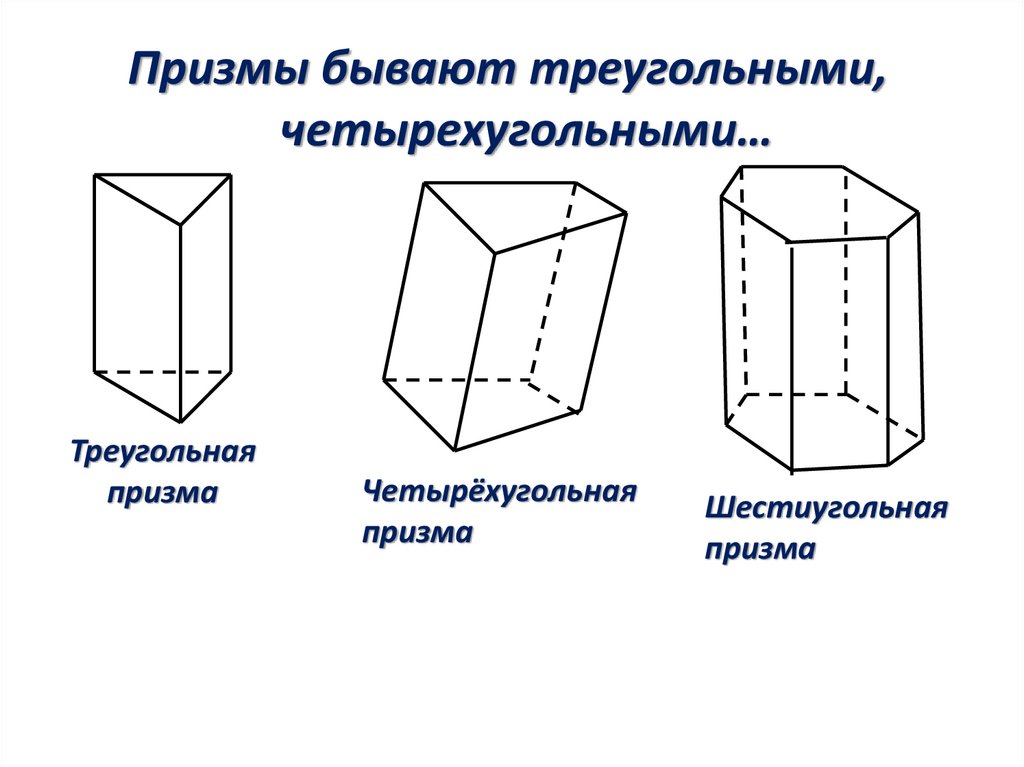
Призмы бывают треугольными,четырехугольными…
Треугольная
призма
Четырёхугольная
призма
Шестиугольная
призма
13.
Наклонная призма- это призма, боковые рёбра которой
не перпендикулярны основанию.
h
14.
Прямая призма- это призма, боковые рёбра
которой перпендикулярны
основанию
Её высота равна
боковому ребру
Боковые грани
h
прямоугольники
b
15.
Правильная призма- это прямая призма, основанием
которой является правильный
многоугольник.
В основании
равносторонний
треугольник
В основании
квадрат
В основании
правильный
6-угольник
16.
Поверхность призмыПолная поверхность Sполн.
+
Боковая
поверхность Sбок
Sп 2Sосн Sбок
Поверхность
оснований Sосн
Sбок S1 S2 S3 ...
17.
Боковая поверхность прямойпризмы
Теорема:
Боковая поверхность прямой призмы
равна произведению периметра
основания на длину бокового ребра.
Дано: прямая n-угольная призма, a1 , а2 … аn стороны основания, H - боковое ребро.
Доказать: Sбок=Pосн H
18.
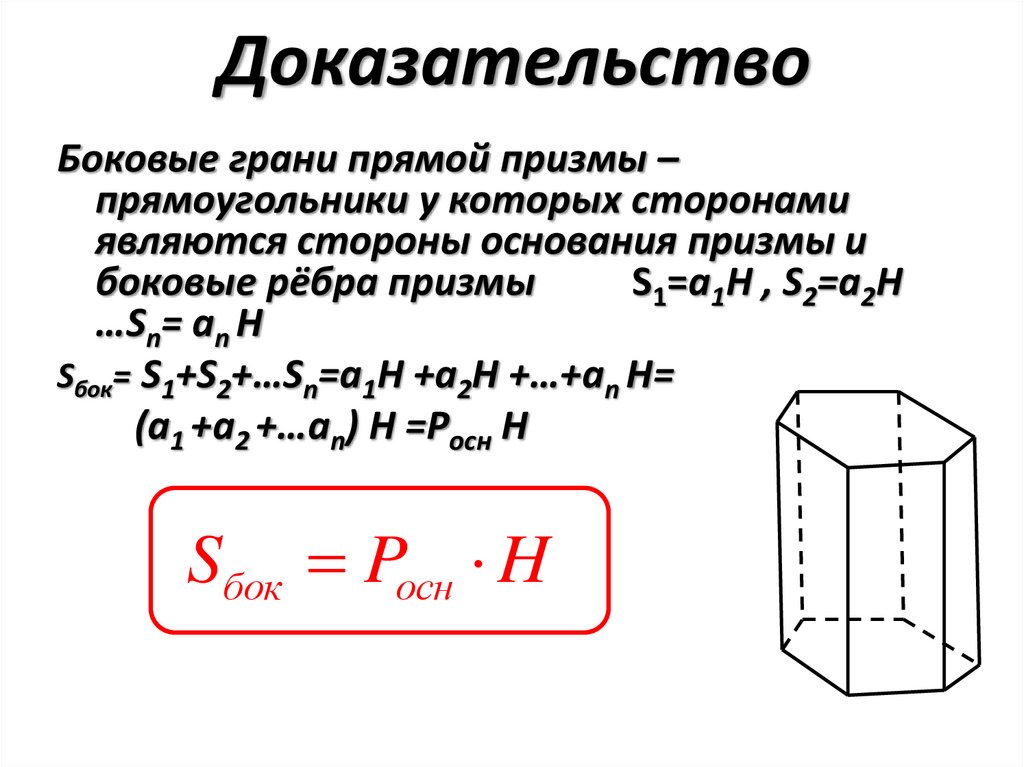
ДоказательствоБоковые грани прямой призмы –
прямоугольники у которых сторонами
являются стороны основания призмы и
боковые рёбра призмы
S1=a1H , S2=a2H
…Sn= an H
Sбок= S1+S2+…Sn=a1H +a2H +…+an H=
(a1 +a2 +…an) H =Pосн H
Sбок Pосн H
19.
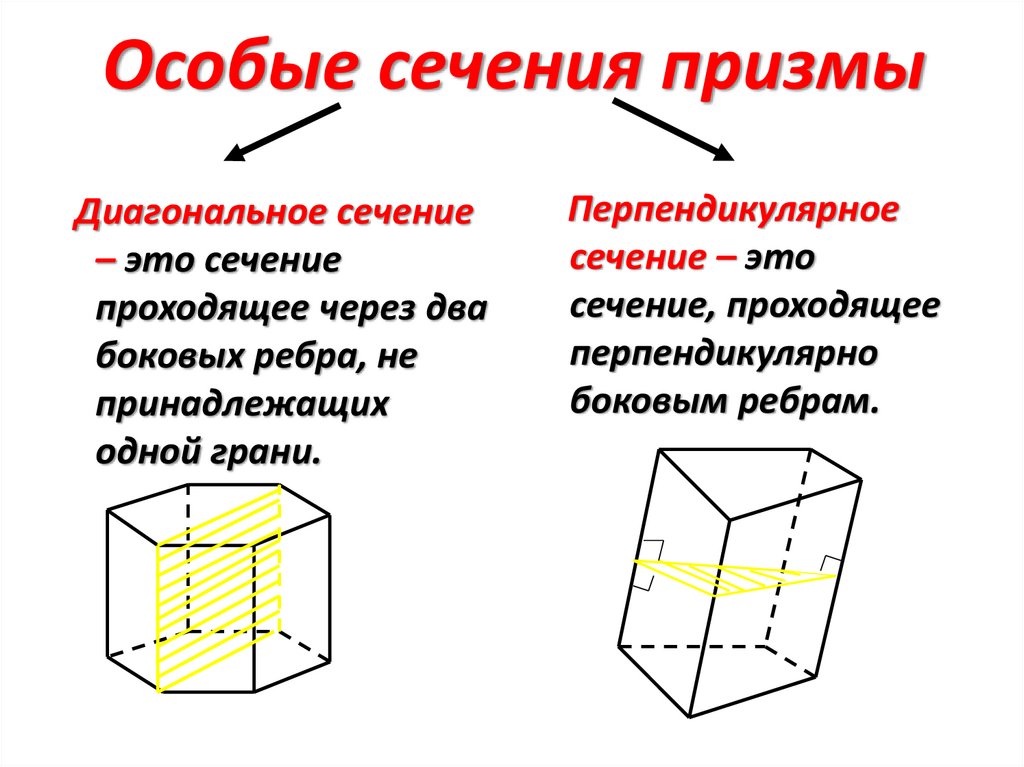
Особые сечения призмыДиагональное сечение
– это сечение
проходящее через два
боковых ребра, не
принадлежащих
одной грани.
Перпендикулярное
сечение – это
сечение, проходящее
перпендикулярно
боковым ребрам.















 Математика
Математика








