Похожие презентации:
Идеальные газы тождественных частиц. Распределение Ферми-Дирака и Бозе-Эйнштейна
1. Идеальные газы тождественных частиц. Распределение Ферми-Дирака и Бозе-Эйнштейна
2.
Частицы тождественные – физически неразличимые => Возможны только такиесостояния системы тождественных частиц, которые не изменяются при
перестановке местами двух частиц => при перестановке двух тождественных
частиц волновая функция может изменяться только на несущественный фазовый
множитель
1 , , j , , i , exp(i ) 1 , , i , , j ,
exp( 2i ) 1 , , j , , i , exp( 2i ) 1 exp(i ) 1
При перестановке местами координат двух частиц волновая функция системы
тождественных частиц может либо менять знак, либо оставаться неизменной
1 , , j , , i , 1 , , i , , j ,
Симметрия волновой функции относительно перестановки координат
тождественных частиц остается постоянной во времени
Pˆi , j 1 , , j , , i , 1 , , i , , j ,
Hˆ 1 , , i , , j , Hˆ 1 , , j , , i , Hˆ , Pˆi , j Hˆ Pˆi , j Pˆi , j Hˆ 0
dPˆi , j
dt
Pˆi , j
t
i ˆ ˆ
H , Pi , j 0
3.
Перестановочная симметрия определется величиной спина частиц системы1) Фермионы (частицы с полуцелым спином). Волновая функция обязательно
является антисимметричной относительно перестановки координат двух частиц
1 , , j , , i , 1 , , i , , j ,
2) Бозоны (частицы с целым спином). Волновая функция обязательно является
симметричной относительно перестановки координат двух частиц
1 , , j , , i , 1 , , i , , j ,
Различие в перестановочной симметрии волновых функций фермионов и
бозонов приводит к принципиальному различию системы тождественных
фермионов и системы тождественных бозонов
4.
Газ идеальный Hˆ Hˆ 1 ( i )i
Hˆ 1 ( )
- одночастичный Гамильтониан (гамильтониан одной отдельно взятой)
частицы в тех же силовых полях, что и весь газ)
Переменные в УШ разделяются
Hˆ 1 ( ) ( ) , ( ) - одночастичный энергетический спектр и
волновые функции одночастичных
стационарных состояний
Одночастичное стационарное состояние - (стационарных состояний одной отдельно
взятой частицы в тех же силовых полях, что и весь газ)
E N ;
1 , i , , N 1 ( 1 ) 1 ( 2 ) N ( N )
- решение УШ для газа.
Однако оно не удовлетворяет перестановочной симметрии, и, следовательно не
является волновой функцией системы тождественных частиц. Следовательно,
нужно брать линейные комбинации соответствующий произведений
1 , i , , N С p 1 ( 1 ) 1 ( 2 ) N ( N )
p
Коэффициенты С нужно подобрать так, чтобы волновая функция обладала
соответствующей симметрией относительно перестановки координат двух частиц
(для фермионов была антисимметричной для бозонов симметричной)
5.
Фермионы1 , 2 1 , 2 C1 1 1 2 2 C2 2 1 1 2
1 , 2 1 , 2 1 , 2 2 , 1
C1 1 1 2 2 C2 2 1 1 2 C1 1 2 2 1 C2 2 2 1 1
C2 C1
1 , 2 1 , 2 C 1 1 2 2 2 1 1 2
d d , 1 C 1
2
d 1
, , , С ( )
2
1
1 , 2
2
1
2
2
1
i
j
N
p
p
N
i i 1
1
1 ( 1 ) 1 ( 2 )
1 2 ( 1 ) 2 ( 2 )
N!
N ( 1 ) N ( 2 )
1
1
( 2 ) N ( N ) 1 , i , j , 1 , j , i ,
1 ( N )
2 ( N )
; E N ; N N
N ( N )
В стационарном состоянии всего ферми-газа каждый фермион находится в одном
из одночастичных стационарных состояний. Стационарное состояние всего
ферми-газа (его микросостояние) можно задать, указав число фермионов в
каждом из стационарных состояний (числа заполнения стационарных состояний)
6.
Возможно ли микросостояние ферми-газа, в котором оба фермиона находятся водном и том же стационарном состоянии?
i i 1
N
( 1 ) ( 2 )
1 ( 1 ) ( 2 )
N!
( 1 ) ( 2 )
1
1
2
2
N
N
1 ( N )
2 ( N )
N ( N )
N
i j i i 1 0 Принцип запрета Паули (в одном и том же
одночастичном стационарном состоянии
одновременно не может находиться более одного
фермиона)
В ферми-газе число заполнения одночастичного состояния может принимать
только два значения
N 0 - состояние пустое
N 1 - в состоянии есть один фермион
7.
Бозоны, 1 , 2 C1 1 2 C2 1 2
1
2
1
2
1
2
2
, 1 , 2 , 2 , 1
1
1
2
C1 1 1 2 2 C2 2 1 1 2 C1 1 2 2 1 C2 2 2 1 1
C2 C1
, 1 , 2 C 1 2 1 2
1
2
1
2
d 1d 2 1 , 2 1 , 2 1
2
1
2
d 1
2
C
1
2
1 , i , j , N С p ( 1 ) ( 2 ) ( N ) 1 , i , j , 1 , j , i ,
1
p
N
i i 1
1/ 2
N 1 ! N 2 !
N!
p
1
1
N
( 1 ) 1 ( 2 ) N ( N ); E N ; N N
В стационарном состоянии всего бозе-газа каждый бозон находится в одном из
одночастичных стационарных состояний. Стационарное состояние бозе-газа (его
микросостояние) можно задать, указав число фермионов в каждом из
стационарных состояний (числа заполнения стационарных состояний) . В случае
бозе-газа нет ограничения на числа заполнения одночастичного состояния.
8.
В стационарном состоянии идеального газа из тождественных частиц каждая изчастиц находится в одном из одночастичных стационарных состояний
(стационарном состоянии одной отдельно взятой частицы в тех же самых
силовых полях, что и весь газ). Микросостояние всего газа в целом можно
задать, указав числа заполнения одночастичных стационарных состояний
E N N ; N N N
В ферми-газе действует фундаментальное ограничение на значения чисел
заполнения одночастичных стационарных состояний – Принцип запрета Паули,
согласно которому в одном и томже одночастичном состоянии одновременно не
может находиться более одного фермиона.
В бозе-газе такого ограничения на числа заполнения нет.
9.
1E N N N
W N exp
; Q
Q
E N N N
exp
N N
N
E N N N
exp
exp
exp
N
exp
N
Q
N
Q
q ;
exp
N
q
N
N 1
N 2
( )
exp
N
N i
exp
N
10.
Qq ; q
W N
N
( )
exp
N
1
E N N N
exp
Q
( )
exp
N
w ( N )
q
1) Фермионы Nℓ =0,1
q
1
w (N )
- вероятность того, что в состоянии ℓ есть Nℓ частиц
( )
N 1 exp
exp
N 0
ln Q ln 1 exp
( )
exp
1
w ( N 1)
- вероятность того, что состояние ℓ
1 exp
exp
1 занято фермионом
1
w ( N 0)
1 w ( N 1) - вероятность того, что состояние ℓ
пустое
1 exp
11.
w N1
exp
N
1 exp
1
N
N w N w N 1
N 0
N w N 1
1
exp
1
1
exp
1
- распределение Ферми-Дирака
ln Q ln 1 exp
1
N
N
NF
exp
1
1
E
N
N
exp
1
1
NF
функция Ферми N N F
exp
1
N
F
12.
Qq ; q
W N
N
( )
exp
N
1
E N N N
exp
Q
( )
exp
N
w ( N )
q
w (N )
- вероятность того, что в состоянии ℓ есть Nℓ частиц
2) Бозоны Nℓ =0,1,2,…
( )
q exp
N
N 0
Ecлc 0 , то для ряд расходится в бозе газе 0 основной уровень энергии
1
( )
( )
q 1 exp
exp 2
( )
1 exp
ln Q ln 1 exp
13.
Вероятность того, что в состоянии ℓ находится Nℓ бозоновexp N
w ( N )
;
q
1
N Nw ( N )
q
N 0
1
q
q
1
;
1 exp
1
N
exp
N
q
N 0
exp N
N 0
1
exp N 1 exp
1 exp
N 0
1
exp
1
1
N
N
NB
exp
1
1
E
N
N
N F
exp
1
1
NB
функция Бозе Эйнштейна N N B
exp
1
N
14.
Идеальный газ из тождественных частицдля фермионов
1
N
;
для бозонов
exp
1
верхний знак фермионы
ln 1 exp
;
нижний знак бозоны
Ai
ai
N
E
N
F/B
N
N
Нужно вычислять f ( )
F/B
15.
Нужно вычислять f ( )Нужно перейти от суммирования по квантовым числам к интегрир. по энергии
d f ( ) f (
)
f ( ) d f ( ) d f ( )
d g f ( ), g
0
1, 0 0
d g d 0, иначе
0
0
d g 1
0
0 0
- число состояний с энергией в интервале ε0-ε0+Δ ε
g - плотность одночастичных стационарных состояний
dN g d - Число состояний с энергией в физ. беск. малом интерв
16.
f (N
) d g ( ) f ( ), g
N
F/B
N
( ) d g ( ) N F / B ( )
E
F/B
( ) d g ( ) N F / B ( )
ln 1 exp
d
g
(
)
ln
1
exp
Через плотность состояний можно выразить любую макроскопическую
характеристику. Особенности в плотности состояний проявляются в
наблюдаемых величинах.
Идеальный ферми-газ можно описать, если известны плотность одночастичных
стационарных состояний и химический потенциал
17.
Конденсация бозе-Эйнштейна1
2k 2
Nk
; k
2m
exp k
1
N , k 0
Т 0 Nk
0, k 0
1
1
T 0 N0
ln
1
N0
exp 1
При достаточно низких температур ах, когда N 0 1,
мал по сравнению с первым возбужденн ым состоянием . 0
N0
18.
N N0k
1
exp k
V
4 dk
3
2
0
1
dk
2 2
k
1
exp
2m
k2
2k 2
1
exp
2m
2k 2
Замена x
2m
m3 / 2
N N 0 V
2 2 2
N 0 N 1
0
V
3
2
1
3/ 2
x1 / 2
1
dx
N 3 / 2
exp x 1 N
0
1
m3 / 2
;
V
2 2 2
0
x1 / 2
1
dx
exp x 1 N
0
2/3








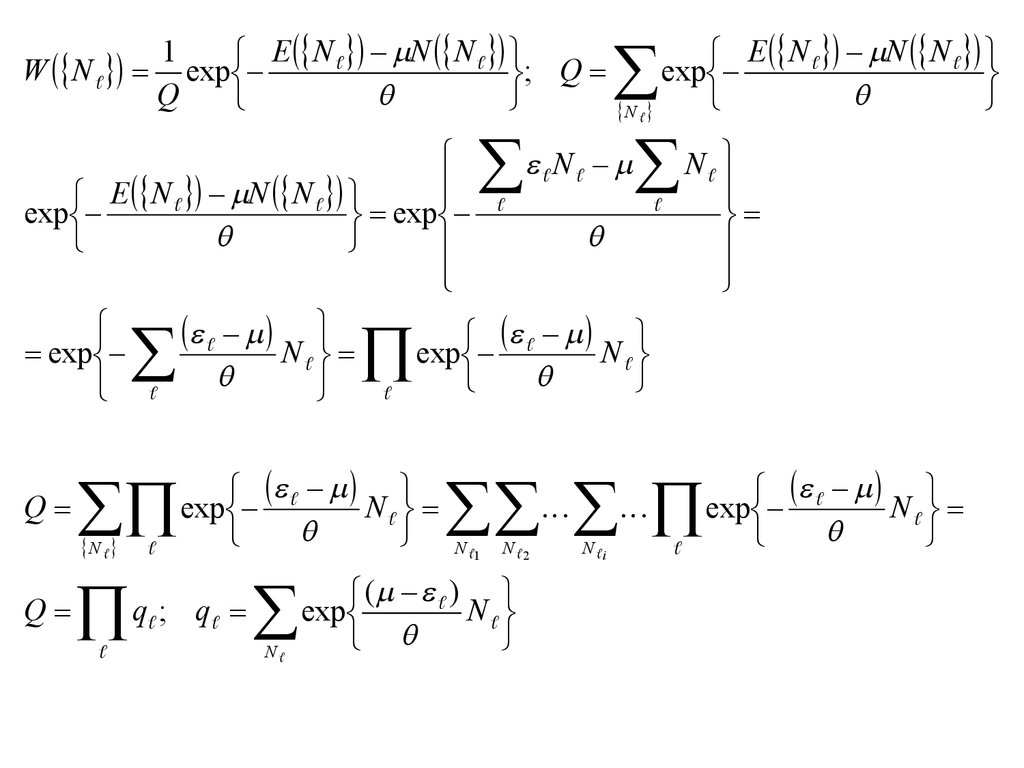









 Физика
Физика








