Похожие презентации:
Комплексные числа
1.
2.
Основные понятияx 1 0 x1, 2 i
2
i 1
- мнимая единица (i - от французского imaginaire
«мнимый»)
Комплексным числом называется выражение вида
а - называется действительной частью числа z, a Re z
z a ib , где a, b - действительные числа, i 2
b - называетсямнимая
мнимойединица,
частью числа
i z, 1b. ) Im z
Выражение z a ib называют алгебраической
формой записи комплексного числа
3.
Основные понятияz a ib
Если a = 0, то ib – чисто мнимое число.
Если b = 0, то получаем действительное число а.
Комплексные числа
z a ib , z a ib ,
которые отличаются только знаком мнимой части,
называются сопряженными
4.
Основные понятияДва комплексных числа z1 a1 ib1 , z 2 a2 ib2
считаются равными, если равны их действительные
и мнимые части соответственно.
a1 a 2
z1 z 2
b1 b2
Комплексное число равно нулю тогда и только
тогда, когда действительная и мнимая части равны
нулю.
a 0
z 0
b 0
5.
Геометрическое изображениекомплексного числа
аргумент комплексного числа
j Argz
z a ib
y
модуль комплексного числа
r z a b
2
2
M (a;b)
z
r
a r cos j ,
b
b r sin j ,
j
О
a
x
b
tgj
a
6.
Алгебраическая, тригонометрическая формазаписи комплексного числа
z a ib
a r cos j ,
b r sin j ,
Выражение z r (cos j i sin j )
называется тригонометрической
формой записи комплексного
числа
z r cos j ir sin j r (cos j i sin j )
7.
Алгебраическая, тригонометрическая и формазаписи комплексного числа
- алгебраическая форма;
z a ib
z r (cos j i sin j )- тригонометрическая форма;
8.
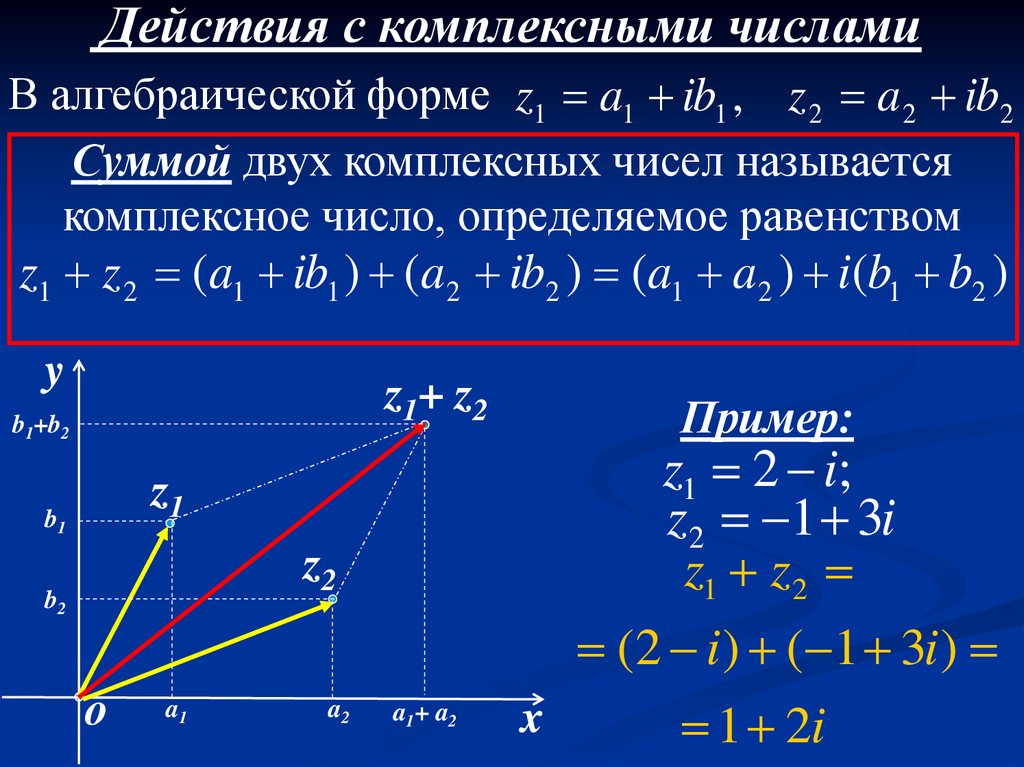
Действия с комплексными числамиВ алгебраической форме z1 a1 ib1 , z 2 a 2 ib2
Суммой двух комплексных чисел называется
комплексное число, определяемое равенством
z1 z 2 (a1 ib1 ) (a2 ib2 ) (a1 a2 ) i(b1 b2 )
y
z1+ z2
b1+b2
z1
b1
z2
b2
о
a1
a2
a1+ a2
Пример:
z1 2 i;
z2 1 3i
z1 z 2
(2 i ) ( 1 3i )
x
1 2i
9.
Действия с комплексными числамиПроизведением комплексных чисел называется
такое комплексное число, которое получается, если
перемножить числа как многочлены, учитывая, что
i 1 .
2
z1 z 2 (a1 ib1 )( a2 ib2 ) a1a2 ib1a2 ia1b2 i b1b2
2
Пример: получим
после преобразования,
(
3
2
i
)(
1
i
)
3
3
i
2
i
2
i
z1 z 2 (a1 a 2 b1b2 ) i(b1 a 2 a1b2 )
3 2 i ( 3 2) 5 i
2
Произведение сопряженных комплексных чисел
равно квадрату модуля каждого из них.
z z z z
2
2
10.
Действия с комплексными числамиЧастным от деления z1 на z2 называется
комплексное число z , удовлетворяющее условию:
z1 z2 z a1 ib1 (a2 ib2 )( x iy )
a1a2 b1b2
Можно доказать, что x 2 2 ,
a2 b2
Тогда,
Пример:
b1a2 a1b2
y 2 2 .
a2 b2
a1 a 2 b1b2
b1 a 2 a1b2
z
i 2
2
2
2
a 2 b2
a 2 b2
2 3i (2 3i )(1 2i ) 2 3i 4i 6 4 7i
4 7
i
1 2i (1 2i )(1 2i )
5
5
5 5
11.
Действия с комплексными числамиВ тригонометрической форме
z1 r1 (cos j1 i sin j1 )
z2 r2 (cos j2 i sin j2 )
При умножении комплексных чисел в тригонометрической форме их модули перемножаются, а
аргументы складываются
z1 z2 r1 r2 (cos(j1 j 2 ) i sin( j1 j 2 ))
12.
Действия с комплексными числами.Формула Муавра
Для нахождения частного двух комплексных чисел
в тригонометрической и показательной форме
применяют следующие формулы:
z1 r1
(cos(j1 j 2 ) i sin( j1 j 2 )),
z 2 r2
В силу правила умножения комплексных чисел
получим:
n
n
z r (cos nj i sin nj ) - формула Муавра












 Математика
Математика








