Электричество и магнетизм (Лекция 10)

1.

Электричество и магнетизм
Лекция 10
Магнитное поле (2)
03 ноября 2021 года
Лектор: доцент НИЯУ МИФИ,
Ольчак Андрей Станиславович

2.

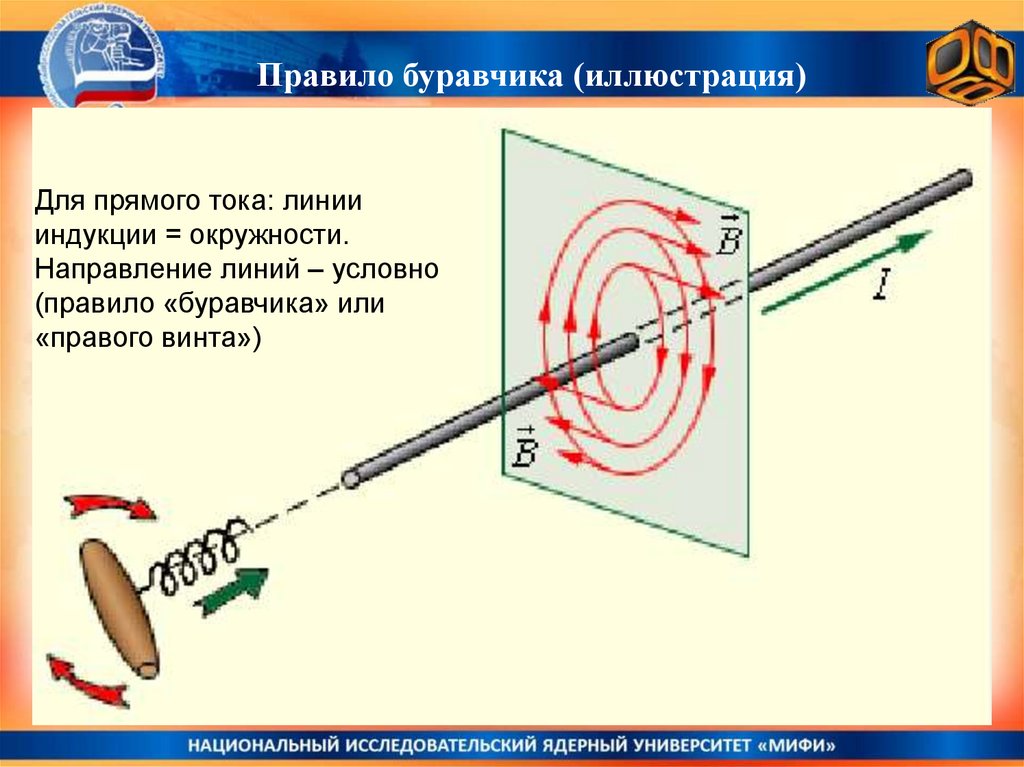
Правило буравчика (иллюстрация)
Для прямого тока: линии
индукции = окружности.
Направление линий – условно
(правило «буравчика» или
«правого винта»)

3.

Магнитное поле
(1) Магнитное поле создаётся движущимися
электрическими зарядами:
Закон Био – Савара –Лапласа

4.

Закон Био – Савара - Лапласа
Магнитное поле равномерно движущегося заряда
R t r r t
v
q
R t
r t
B t
0 q v, R
Опыт: B
4
R3
r
O
0 4 10 7 Гн/м - магнитная постоянная
Гн = Н·м/А2

5.

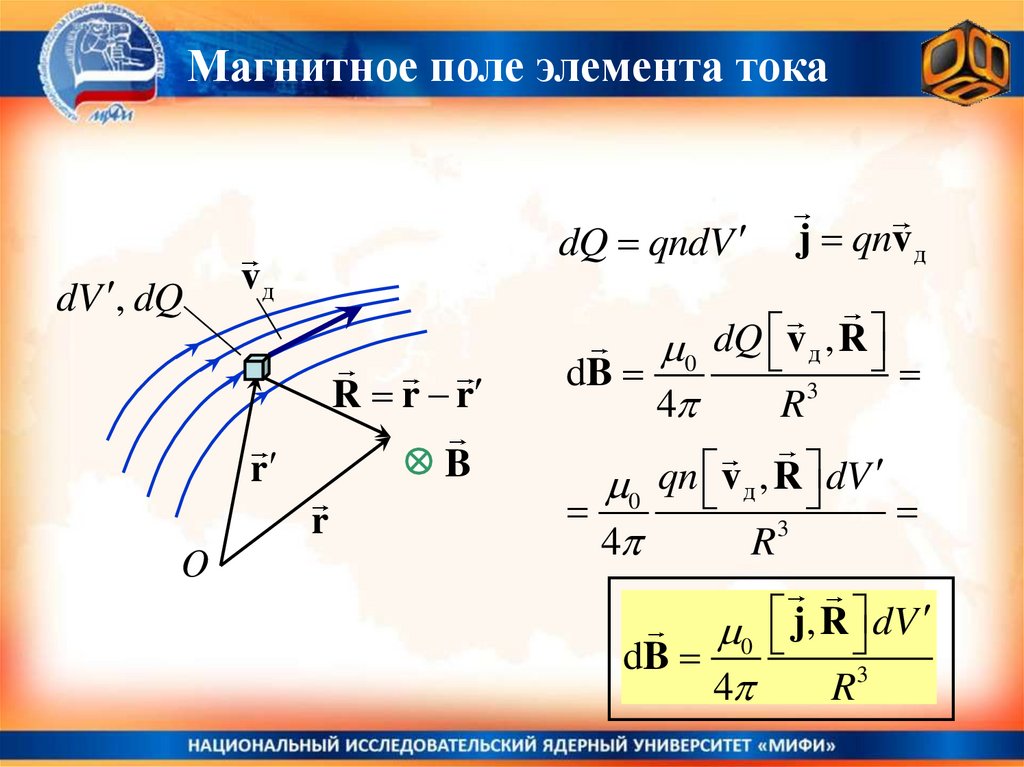
Магнитное поле элемента тока
dV , dQ
dQ qndV
vд
R r r
r
B
r
O
j qnv д
0 dQ v д , R
dB
3
4
R
0 qn v д , R dV
3
4
R
0 j, R dV
dB
4
R3

6.

Закон Био – Савара - Лапласа
Магнитное поле объемного
тока
dV , dQ
R r r
vд
R r r
r
B
r
O
0 j, R dV
dB
4
R3
Био – Савар (1820, эксперимент)
Лаплас (1826, теория)
j r , r r dV
0
B r
3
4 V
r r
пров

7.

Закон Био – Савара - Лапласа
Магнитное поле линейного проводника с током
I
S
dl
R r r
r
L
dB
r
O
j, d l dl , jdV jSdl
jSd l Id l
dl
I
dl
jdV Id l
0 I d l , R
dB
4
R3
0 I dr , r r
B r
4 L r r 3

8.

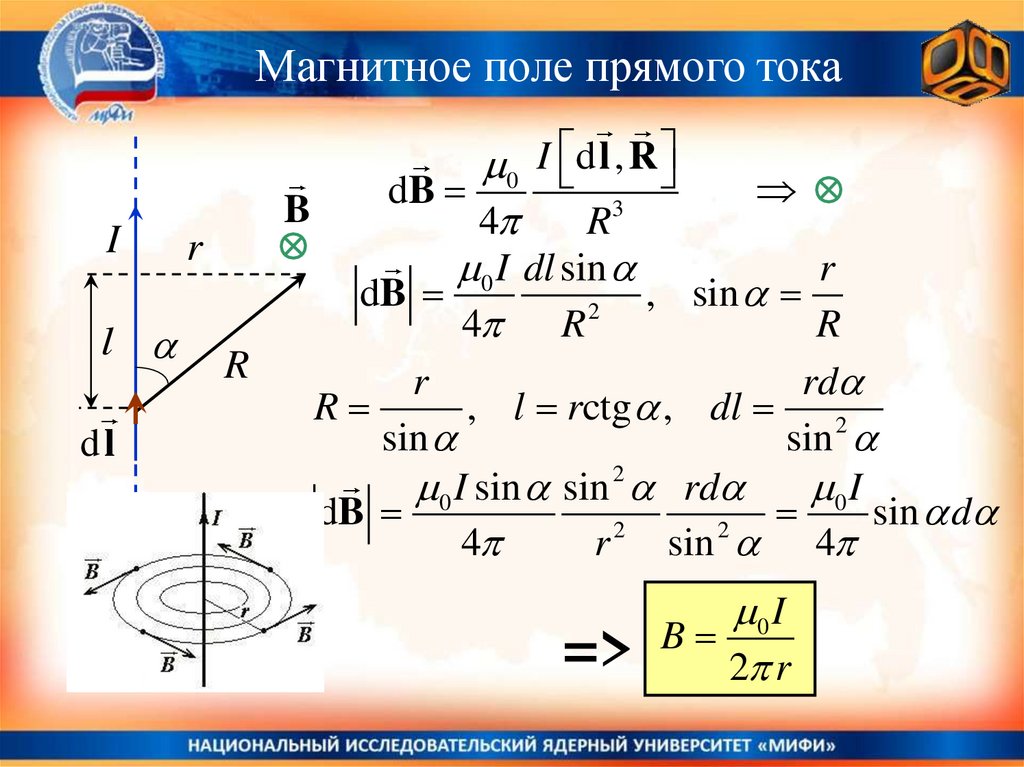
Магнитное поле прямого тока
0 I d l , R
d
B
3
B
4
R
I
r
0 I dl sin
r
dB
, sin
2
4 R
R
l
R
r
rd
R
, l rctg , dl
2
sin
sin
dl
0 I sin sin 2 rd
0 I
dB
sin d
2
2
4
r sin 4
=>
0 I
B
2 r

9.

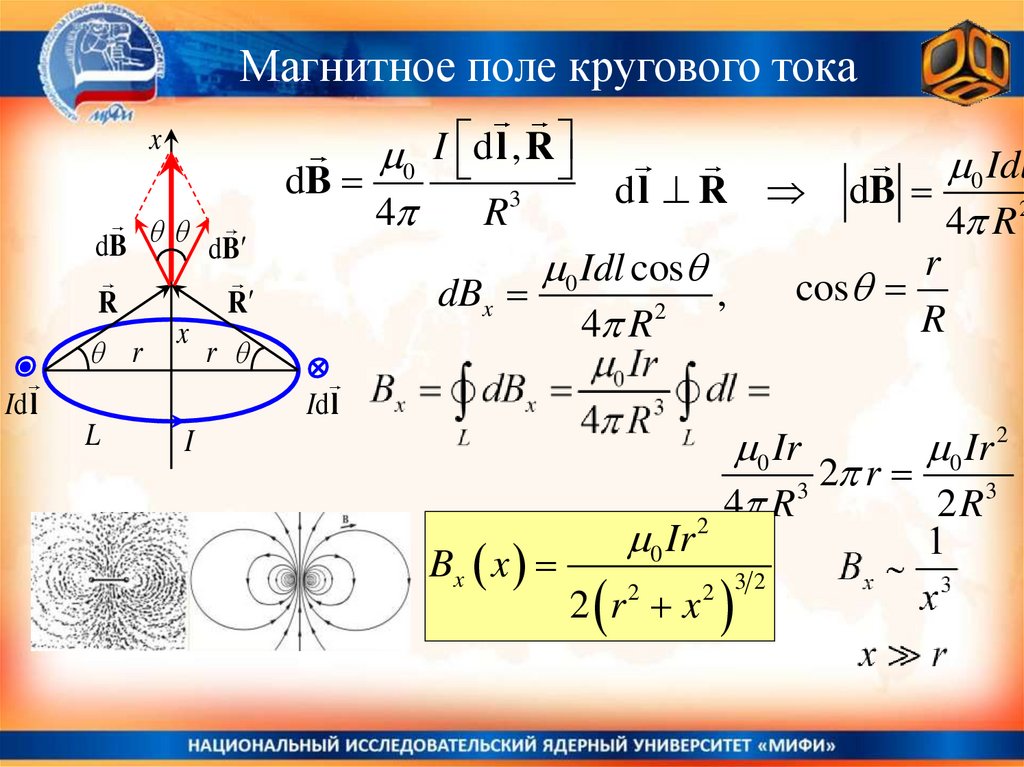
Магнитное поле кругового тока
x
dB dB
R
R
r
x
Id l
r
0 I d l , R
0 Idl
dB
d l R dB
3
4
R
4 R 2
r
0 Idl cos
cos
dBx
,
R
4 R 2
Id l
L
I
Bx x
0 Ir 2
2 r x
2
0 Ir
0 Ir 2
2 r
3
4 R
2R3
2 32

10.

Магнитное поле соленоида (катушки с током)
B
Каждый виток катушки создает в центре
соленоида магнитное поле с индукцией:
B = (μ0/2)I/R
Направление вектора магнитной индукции
определяется по правилу буравчика.
L
R
Вся катушка c числом витков N создаст в
сердечнике соленоида однородное магнитное поле
с индукцией, вычисляемой методом сложения
(интегрирования) полей, создаваемых отдельными
витками. Если катушка достаточно длинна (L >> R)
то результат интегрирования не зависит от R:
B = μ0IN/L

11.

Магнитное поле
(2) Магнитное поле действует на движущиеся
заряды
Сила Лоренца
Закон Ампера

12.

Сила Лоренца
Магнитная сила
Fм q v, B
Fм q vB sin
Сила Лоренца
Fм qE q v, B
B
Fм
v
1. Магнитная сила НЕ совершает
работы
2. Величина и направление векторов
напряженности электрического
поля и магнитной индукции
зависят от выбора системы
отсчета.

13.

Векторное произведение
Fмаг = q[V,B]
Fмаг
B
V
Немного математики:
Векторное произведение с = [ a, b ]
направлено перпендикулярно обоим
векторам a и b и равно по величине
с = a b sin(α), где α - угол между
векторами а и b. Направление вектора
с определяется правилом левой руки.
c
Величина силы действия магнитного поля, соответственно, равна
Fмаг = qVBsin(α), где α - угол между векторами скорости и магнитной
индукции.
b
a

14.

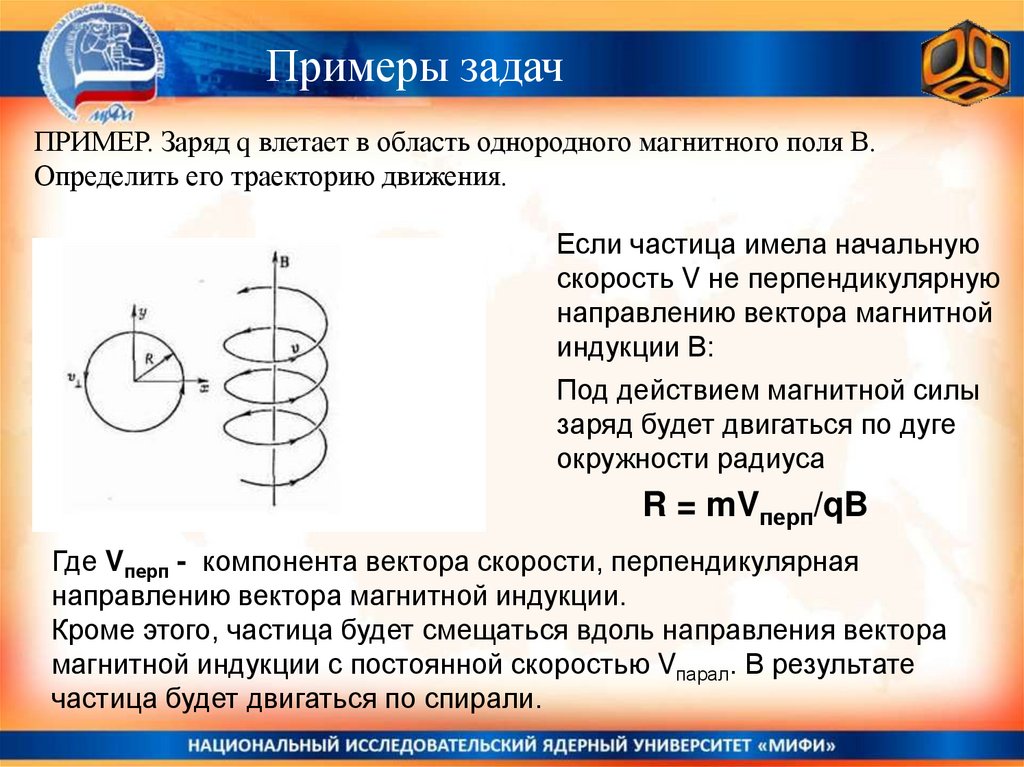
Примеры задач
ПРИМЕР. Заряд q влетает в область однородного магнитного поля В.
Определить его траекторию движения.
Если частица имела начальную
скорость V не перпендикулярную
направлению вектора магнитной
индукции В:
Под действием магнитной силы
заряд будет двигаться по дуге
окружности радиуса
R = mVперп/qB
Где Vперп - компонента вектора скорости, перпендикулярная
направлению вектора магнитной индукции.
Кроме этого, частица будет смещаться вдоль направления вектора
магнитной индукции с постоянной скоростью Vпарал. В результате
частица будет двигаться по спирали.

15.

Примеры решения задач
Пример 2. Скорости v двух нерелятивистских электронов
одинаковы и перпендикулярны прямой, которая их соединяет.
Найти отношение сил магнитного и электрического
взаимодействия электронов.
v
e
Fм
R t
B t
Fэл
0 e v, R
0 ev
B
B
3
2
4
R
4 R
0 e 2 v 2
Fм e v, B Fм
4 R 2
2
2
e R
e
Fэл
Fэл
3
4 0 R
4 0 R 2

16.

Примеры решения задач
Пример 2. Скорости v двух нерелятивистских электронов
одинаковы и перпендикулярны прямой, которая их соединяет.
Найти отношение сил магнитного и электрического
взаимодействия электронов.
v
e
Fм
R t
Fм 0 e2 v 2 4 0 R 2
2
2
Fэл
4 R
e
B t
Fэл
ВНИМАНИЕ. μ0ε0 = 1/с2; c = 3*108 м/с –
скорость света в вакууме (!)

17.

Закон Ампера
Магнитная сила, действующая на элемент тока
dFм dQ v др B
dV , dQ
vд
dQ qndV
dFм qn v др B dV j B dV
j
dFА j B dV
B
FА
Vпров
j B dV

18.

Закон Ампера
Закон Ампера для элемента линейного проводника
jdV Id l
dFА I d l B
FА I d l B
L
Андре́-Мари́ Ампе́р
1775-1836

19.

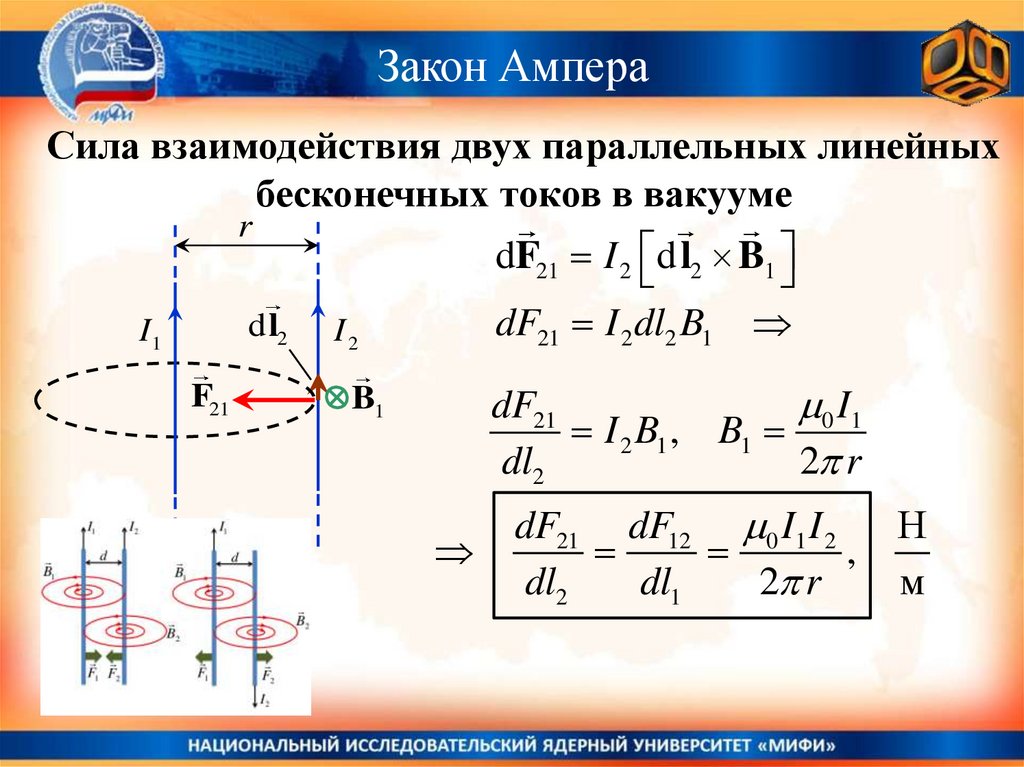
Закон Ампера
Сила взаимодействия двух параллельных линейных
бесконечных токов в вакууме
r
dF21 I 2 d l2 B1
dl2
I1
F21
dF21 I 2 dl2 B1
I2
0 I 1
dF21
I 2 B1 , B1
dl2
2 r
B1
dF21 dF12 0 I1 I 2
,
dl2
dl1
2 r
Н
м

20.

Закон Ампера
Единица силы тока в системе СИ
Прохождение тока силой в 1 Ампер по двум очень
длинным тонким параллельным проводникам,
находящимся в вакууме на расстоянии 1 метр друг от
друга, вызывает силу взаимодействия F = 2 •10-7 Н на
каждом участке проводника, длиной в 1 метр.
dF21 0 I1 I 2
dl2
2 r
7
4
10
1 1
7
2 10
2 1
1 Кулон – это заряд, проходящий за 1 с через поперечное сечение
проводника, по которому течёт постоянный ток силой I = 1 А.

21.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!

22.

Вспоминаем: теорема Гаусса.
Поток вектора напряженности электрического поля через
замкнутую поверхность равен алгебраической сумме
заключенных внутри этой поверхности зарядов, деленной
на электрическую постоянную ɛ0 = 4πk
1
N
EdS q
S
0 i 1
i
divE = dФ/dV =
= (Σ qi / ɛ0 )dV =
= ρ / ɛ0
div E
0
Дивергенция вектора напряженности электрического поля
в точке равна плотности электрического заряда в данной
точке, деленной на электрическую постоянную ɛ0.

23.

Теорема Остроградского-Гаусса
Факт: поток через внешнюю поверхность
группы микро-кубиков = сумме потоков
через поверхности всех микро-кубиков
Vi
V
V
N
Га́усс И. К. Ф.
(1777-1855)
N
u dS
S
i 1
i
div ui Vi div u dV
i 1
V
NV 0
i
Острогра́дский
М. В. (1801-1861)
u dS div u dV
S
V

24.

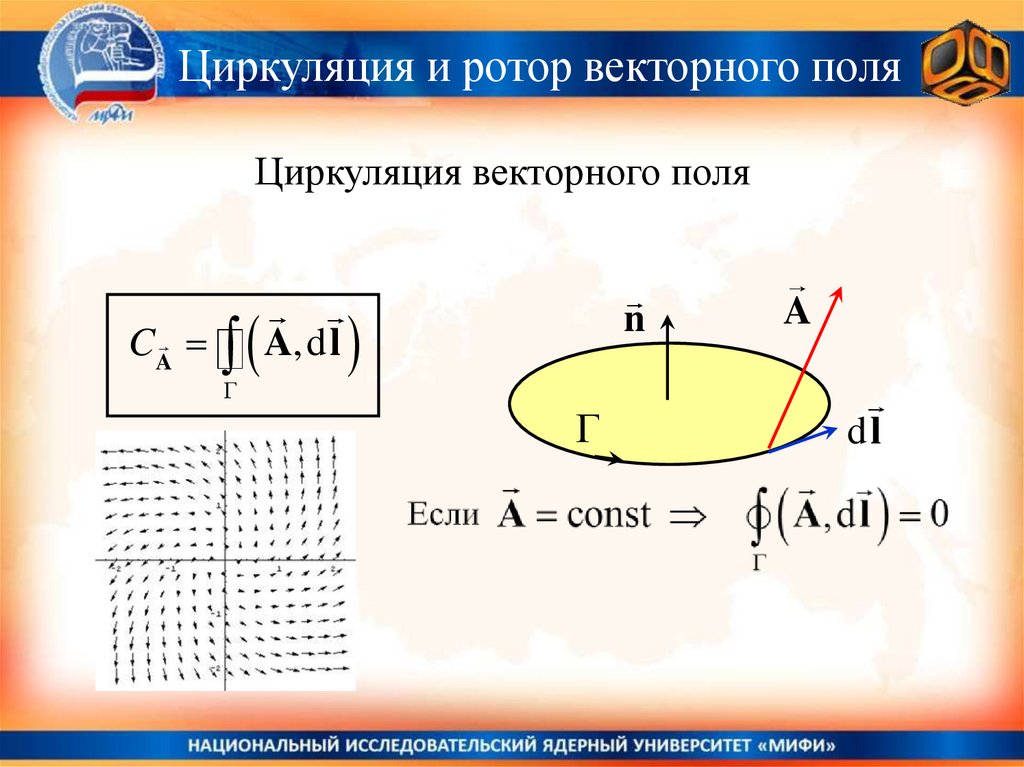
Циркуляция и ротор векторного поля
Циркуляция векторного поля
CA
A,d l
n
A
dl

25.

Циркуляция и ротор векторного поля
Ротор векторного поля
A,d l
lim
rot A
S 0
n
S
S
f
Можно доказать, что этот предел ведёт
себя как проекция некоторого вектора,
называемого ротором, на нормаль n к
площадке.
rot A, n lim
S 0
A,d l
S

26.

Циркуляция и ротор векторного поля
Компоненты ротора в декартовых координатах
z
1
2
O
4
z
?
z
x
3
x x
x
y
x
rot A
n
n z
y y y
y
1
4
n
2
3
A,d l ?

27.

Циркуляция и ротор векторного поля
z
x
x x
x
y y y
y
1
x x
2
A,d l
1
4
4
x
A,d l
n
3
Ax dx
x x
Ax x, y y x
3
2
x
Ax dx Ax x, y x
1
y
4
3
y y
y y
2
y
A,d l
A,d l
Ay dy Ay x, y y
Ay dy Ay x x, y y

28.

Циркуляция и ротор векторного поля
A,d l A x, y A x, y y x
A x x, y A x, y y
x
x
y
z
x
x x
x
y
y y y
y
1
4
n
2
3
S 0
Ay
Ax
x y
x y
y
x
Ay Ax
S S x y
y
x

29.

Циркуляция и ротор векторного поля
x
y
z
Az Ay
rot A
y
z
x
Ax Az
rot A
z
x
y
Az Ay
Ay Ax
Az Ax
rot A
ex
ez
ey
z
z
y
x
y
x
ex
ey
ez
rot A , A
x
Ax
y
Ay
z
Az
Векторное поле
называется вихревым,
если ротор этого поля
НЕ равен нулю
тождественно.

30.

Циркуляция и ротор векторного поля
Теорема Стокса
A,d l A,d l
N
Si
i 1 i
N
i 1
rot A, dS
S
rot Ai , n Si
i
S
A,d l rot A, dS
S
N
Si 0

31.

Пример вихревого поля
A Ax y ex
Является ли это поле вихревым?
y
z
x
ex
ey
ez
rot A , A
x
Ax
y
Ay
z
Az
Ax
rot A
ez
y

32.

Пример не вихревого поля
Пример. A A r er
Является ли это поле вихревым?
A,d l A r e ,d l
r
0
rot A 0
Из физики:
E, d l 0
rot E = 0 => Электростатическое поле НЕ является вихревым

33.

Основные законы магнитостатики
Теорема Гаусса для вектора магнитной индукции
Опыт показывает, что в природе нет магнитных зарядов,
которые могли бы послужить источниками магнитного поля.
div B 0
Замечание. Опыт показывает, что данные уравнения
справедливы не только для постоянных, но и для переменных
магнитных полей.

34.

Основные законы магнитостатики
Циркуляция и ротор вектора магнитной индукции
Циркуляция по контуру вокруг прямого проводника с током:
dl = rda => rda/r = da =>.
0 I
2 0 I
2
rot B = μ0I/πr2 = j.
Знак плюс, если ток направлен вверх (как и нормаль к контуру
интегрирования)

35.

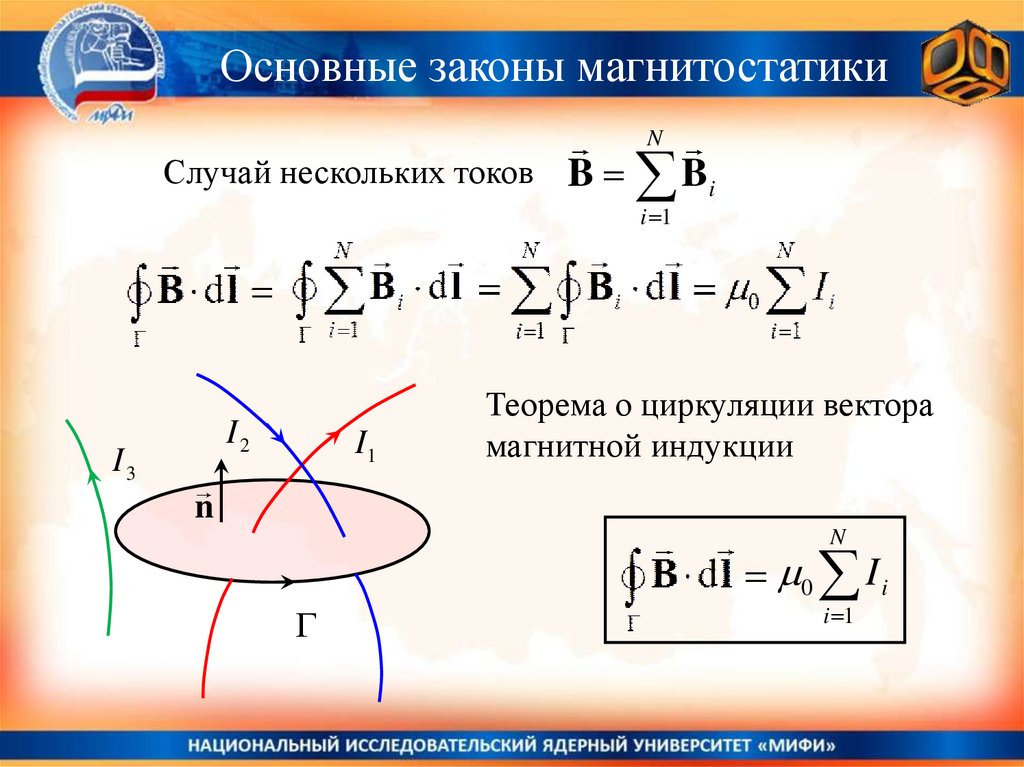
Основные законы магнитостатики
Случай нескольких токов B
N
B
i
i 1
I2
I3
I1
Теорема о циркуляции вектора
магнитной индукции
n
N
0 I i
i 1

36.

Основные законы магнитостатики
Ротор магнитного поля
N
Непрерывное распределение токов
I I i j dS
i 1
S
0 j dS
j
S
S
n
rot B dS j dS
0
S
rot B 0 j
S

37.

Основные законы магнитостатики
Замечание 1. Магнитное поле является вихревым,
поскольку его ротор НЕ равен нулю тождественно.
Замечание 2. Любое векторное вихревое поле (в частности
– магнитное В) можно представить в виде ротора другой
векторной функции: B rot A
Где вектор А называют векторным потенциалом магнитного поля.
Для магнитного поля, создаваемого точечным равномерно
В = (μ0/4π)q[v,r]/r3
A = (μ0/4π)qv/r = μ0ε0φv = φv/с2
ДЗ: проверить формулу!
движущимся зарядом

38.

Магнитная постоянная и скорость света.
μ0 = 4π •10-7 Н/А2 = 12,56 •10-7 Н/А2 - магнитная
постоянная
ε0 = 8,85 •10-12 Кл2/Hм2 - электрическая постоянная (из
закона Кулона)
μ0 ε0 = 1,256 •10-6 • 0,885 •10-11 [Н/А2 • Кл2/Нм2] = 1,1
10-17[с2/м2]
(μ0 ε0) -1/2= (0,11 • 10-16) -1/2[м/с] = 3•108 м/с = с
(скорость света)

39.

Основные законы магнитостатики
Основные законы электростатики и магнитостатики
E
0
B 0
E 0
B 0 j

40.

Дистанционный курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Следующая лекция
10 ноября