Похожие презентации:
Свойства канонического ансамбля. Поступательная сумма и интеграл по состояниям. Формула Закура-Тетроде. Лекция 20
1.
Лекция 20Свойства канонического ансамбля.
Поступательная сумма и интеграл по состояниям.
Формула Закура-Тетроде.
2.
Лекция 19Микроканонический и канонический ансамбли.
Энтропия в каноническом ансамбле.
Статистические суммы по состояниям Z и Q.
3.
Химический потенциал компонента в однокомпонентнойсистеме обладает следующими свойствами
2 балла
Укажите правильный ответ !
1. Убывает с температурой при постоянном давлении.
2. Постоянен при постоянной температуре.
3. Возрастает с температурой при постоянном давлении.
4. В точке фазового перехода первого рода наблюдается скачок
химпотенциала.
5. Является парциальной мольной энтальпией.
4.
1баллаКонстанта равновесия реакции А+В =АВ в растворе
зависит от ….
Отметьте неправильное утверждение !!
1. температуры,
2. растворителя,
3. внешнего давления на раствор,
4. концентрации реагентов и продуктов,
5. выбора стандартных хим.потенциалов для продуктов и
реагентов.
5.
(Т , p, х А 1); (Т , p, х А 1)i
0
i
G RT ln K
0
AB
0
A
0
B
0
0,0,0
G RT ln K
AB
A
B
, ,
6.
A+ B = ABВода растворитель
d ln K , ,
V , ,
dp
RT
T
К , , T ,1бар 1.2 104
К , , T ,1000 бар 2.0 104
Не
A + B = АВ
pвнеш = pвнут = pинерт (1-1000 бар)
T = 1000 K
7.
1 баллаТермодинамическая вероятность, W, по Больцману, это
1. Кинетическая энергия системы
2. Число микросостояний системы
3. Число макросостояний системы
4. Максимальное число микросостояний, доступных
системе при данных условиях (E,N – const)
5. Вероятность попасть в данное микросостояние.
8.
Сумма по состояниям частицы, Q, это:1 балла
1.
W
2.
i
n ln n n
i
i
i
5.
ze
i
i
i
i
i
3.
z e
i
i
i
N!
4.
i ni !
9.
1 баллаМикроканонический и канонический ансамбли.
Какое из утверждений верно?
1. В каноническом ансамбле больше микросостояний.
2. У микроканонического ансамбля меньше энергии.
3. В микроканоническом ансамбле энергия
одинакова во всех микросостояниях.
4. Внутренняя энергия системы – это максимальная
энергия в каноническом ансамбле.
10.
Интеграл по состояниям системы равенZ e
E ( p,q)
kT
d
1 балла
А что такое E (p,q) ?
1.
Это сумма энергий частиц, входящих в систему
2.
Это энергия системы в различных
макросостояниях
3.
Это внутренняя энергия системы, U
4.
Это энергии системы в различных микросостояниях
11.
2 баллаВ системе установилось равновесие Агаз + Вгаз = Авгаз.
Мы увеличиваем общее давление в системе. При этом
изменились парциальные давление р(А), р(В) и р(АВ).
Почему?
1. Изменили общее давление, должны измениться и
парциальные давления.
2. Изменилась константа равновесия, К
3. Газы перестали быть идеальными
4. Правильно (1) и (2)
5. Правильно (1) и (3)
12.
СТАТИСТИЧЕСКИЙ ПОДХОД к ОПРЕДЕЛЕНИЮТЕРМОДИНАМИЧЕСКИХ ВЕЛИЧИН
13.
Фазовое пространство и канонический ансамбльdw =ρ(p,q) dpdq
dw =dn/N
14.
Канонический ансамбльln E ( p, q ) E ( p, q)
Е ( p , q e E ( p , q )
E ( p , q )
Е
(
p
,
q
)
d
1
e
d
1 e
e
E ( p ,q )
Z e
1
d ; e e E ( p ,q ) d Z
e
E ( p ,q )
kT
d
1
E p, q e
Z
U , S f (Z )
E p ,q
kT
15.
Канонический ансамбльF kT ln Z
F
kT ln Z
ln Z
S
k ln Z kT
T V , n T V , n
T V , n
ln Z
2 ln Z
U F TS kT ln Z kT ln Z kT
kT
T
T
V , n
V , n
2
2
U
ln Z
2 ln Z
сv
2kT
kT
2
T
T
T
V , n
V , n
V , n
16.
Канонический ансамбль. Внутренняя энергия.U E ( p, q ) E ( p, q ) Eср
T
Термодинамика : U U 0
c dT
V
T 0
?
17.
E p1q1E p2 q2
E p3q3
E p4 q4
E p1 , q1 E p2 , q2 .....
Eср ?
i
18.
Плотность вероятности по энергииd ( E ) f ( E )dE ;
d E ( p, q ) E p, q d
d ( E ) E p, q d ( E ) E p, q
d ( E )
f E ( E p , q )
dE
d ( E )
dE
dE
19.
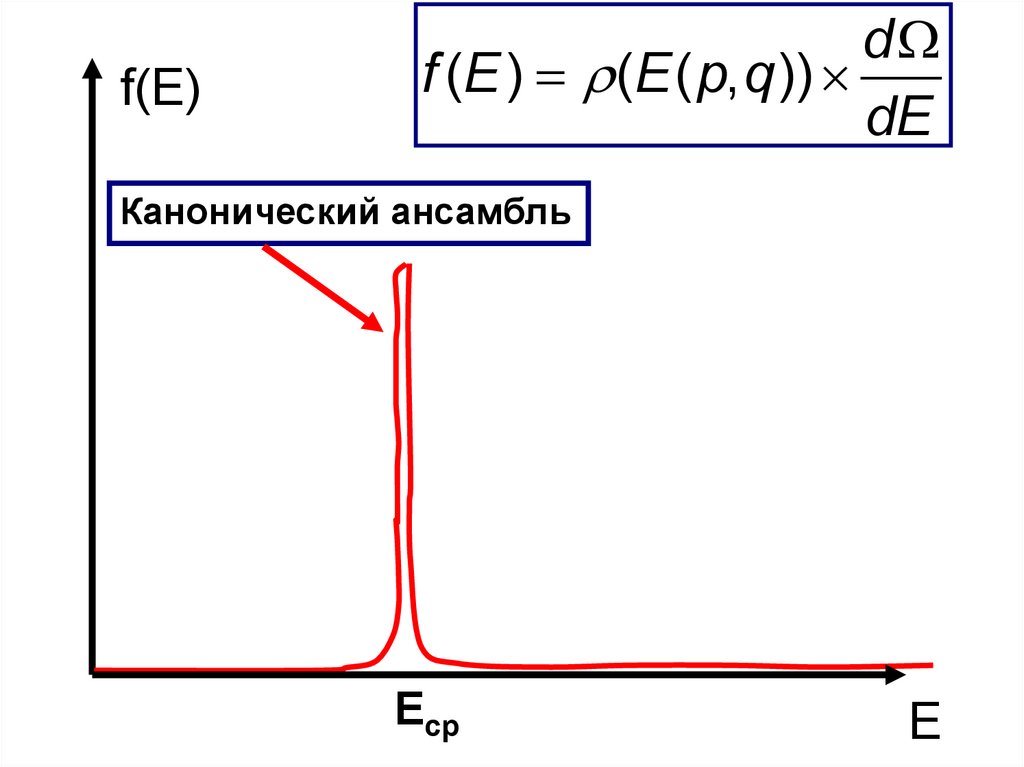
f(E)d
f (E ) (E ( p, q ))
dE
Канонический ансамбль
Eср
E
20.
Канонический ансамбль. Энтропия.E p, q
S k ln ( E )
21.
Канонический ансамбль. Энтропия.S k ln E p, q
( E ( p ,q ))
E ( p, q ) d 1 E ( p, q ) E ( p, q )
ln E p, q ln 0; ln E p, q ln
ln E p, q ln E p, q ln E p, q
S k ln k ln E p, q
22.
Ансамбли…Микроканонический
Канонический
E ( p, q ) const ,
0 E ( p , q ) ,
( E ( p, q) const
U E ( p, q )
S k ln [ E ( p, q)]
1
( E ( p, q ) e
Z
U E ( p, q )
E ( p,q)
kT
S k ln [ E ( p, q)]
23.
f(E0)f(E)
d
f (E ) (E ( p, q ))
dE
f (E )dE 1;
f (E0 ) ; f (E E0 ) 0
E0
E
24.
df (E ) (E ( p, q ))
dE
f(E)
(E ( p, q ) ~ e
E
kT
d (E )
~E
dE
Eср
3N
1
2
E
25.
РАСЧЕТ ИНТЕГРАЛА (СУММЫ) ПО СОСТОЯНИЯМдля
КАНОНИЧЕСКОГО АНСАМБЛЯ
26.
Канонический ансамбльF kT ln Z
F
kT ln Z
ln Z
S
k ln Z kT
T V , n T V , n
T V , n
ln Z
2 ln Z
U F TS kT ln Z kT ln Z kT
kT
T
T
V , n
V , n
2
2
U
ln Z
2 ln Z
сv
2kT
kT
2
T
T
T
V , n
V , n
V , n
27.
Расчет энергии ГельмгольцаF kT ln Z kT ln e
E ( p ,q )
kT
d kT ln e
E0
kT
kT
E0
kT
e
E ( p ,q ) E0
kT
kT ln e
F E0 kT ln e
E ( p , q ) E0
kT
E ( p , q ) E0
kT
d ;
d kT ln Z *
ln Z * ln 0 ; kT ln Z * 0, T 0
d
28.
Расчет энтропии и 3-й закон термодинамики*
F E0
ln
Z
F
*
S
k ln Z kT
T
T V
T V
V
ln 0
k ln 0 kT
k ln 0
T V
∆ 0 – микросостояния, возможные при Т 0
Если ∆ 0 =1 выполняется 3-й закон в формулировке Планка
29.
Связь суммы по состояниям системы Z имолекулярной сумм по состояниям Q
30.
Для каких систем можно рассчитать Z ?1. Идеальные газы, ! , (+)
2. Реальные газы !, ? (±)
3. Жидкость ?
(-)
4. Твердые вещества ?,! (±)
31.
Расчет Z и термодинамических функций дляидеальных газов
32.
Расчет Z и QE ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) 1 ( p1, x ; q1, x ... p1, z ; q1, z ..)
... i ( pi , x ; qi , x ... pi , z ; qi , z ..) .. N ( pN , x ; qN , x ... pN , z ; qN , z ...)
Z e
Ei ( p ,q )
kT
d
N !* h3 N
( p ,q )
( p ,q )
N
1 1 1 dp dq ...dp dq
N N N dp
dq
...
dp
dp
1
Q
1,
x
1,
x
1,
z
1,
z
N
,
x
N
,
x
N
,
z
N
,
z
kT
e kT
.. e
3
3
N ! p1 ,q1
h
h
N!
p N ,q N
Qi
pi ,qi
e
i ( pi ,qi )
kT
dpi , x dqi , x ...dpi , z dqi , z
h3
33.
Расчет Z и Qi ( pi , x ; qi , x .. pi ,вр ; qi ,вр... ) i ,пост ( pi , x ; qi , x ... p1, z ; q1, z )
i ,вр ( pi ,вр ; qi ,вр ..) i ,кол ( pi ,кол ; qi ,кол ) i ,эл ( pi ,эл ; qi ,эл ) i , яд ( pi , яд ; qi , яд )
Qi Qi.пост. Qi , вр. Qi , кол Qi , эл Qi , яд
Q
Z
i , пост.
Qi , вр. Qi , кол. Qi , эл. Qi , яд.
N!
N
34.
СУММА или ИНТЕГРАЛ?ХАРАКТЕРИСТИЧЕСКАЯ ТЕМПЕРАТУРА.
35.
Интеграл или сумма ?i ( pi ; qi ) const
Qi
pi0 pi , qi0 qi
e
i ( p, q )
kT
pi0 , qi0
Qi
pi , qi
e
при pi0 pi pi0 pi ; qi0 qi qi0 qi
i ( p, q )
kT
dpi dqi
hi
dpi dqi
hi
e
i ( p, q )
kT
pi0 pi , qi0 qi
pi0 , qi0
i
dpi dqi
kT
e
gi
i
h
Qi e
i
i
kT
gi
36.
eСумма или Интеграл ?
i
kT
e
1
kT
e
2
e
kT
( p,q)
kT
0
1
2
3
4
5
6
7
n
37.
Характеристическая температура;
k
k
(4)
1
(1)
1
3
1 10 K
3
2
2 10 K 104 K
3
8
38.
Суммирование? Интегрирование?Q ;
T
Q ; T
Q qo ;
T
39.
ПОСТУПАТЕЛЬНАЯ СУММА по СОСТОЯНИЯМ40.
eПоступательная сумма по состоянием
n2
T
e
T
n
2
e
( n 1) 2
T
e
1
x2
T
h2
2
8l mk
1
2
3
4
5
6
7
T
n
41.
Классический расчет поступательного интегралаp 2 mV 2
( p)
2m
2
Qпост. e
( p ,q )
2 kTm
dpx dp y dpz dqx dq y dqz
h
Qпост. e
( p,q)
2 kTm
h
V
3 e
h
px2
2 kTm
e
2 kTm
dpx dp y dpz dqx dq y dqz
h3
dpx dp y dpz dqx dq y dqz
Qпост.
3
px2 p 2y pz2
3
dpx e
V
3 e
h
p 2y
2 kTm
px2 p 2y pz2
dp y e
2 kTm
pz2
2 kTm
dpx dp y dpz
dpz
42.
Классический расчет поступательного интегралаQпост.
V
3 e
h
px2
2 kTm
e
dp y e
dx
a
1/ 2
ax 2
1
;
2mkT
Qпост.
2 kTm
a
dpx e
p 2y
a
1/ 2
2mkT
1/ 2
V
3/ 2
3 2 mkT
h
pz2
2 kTm
dpz
43.
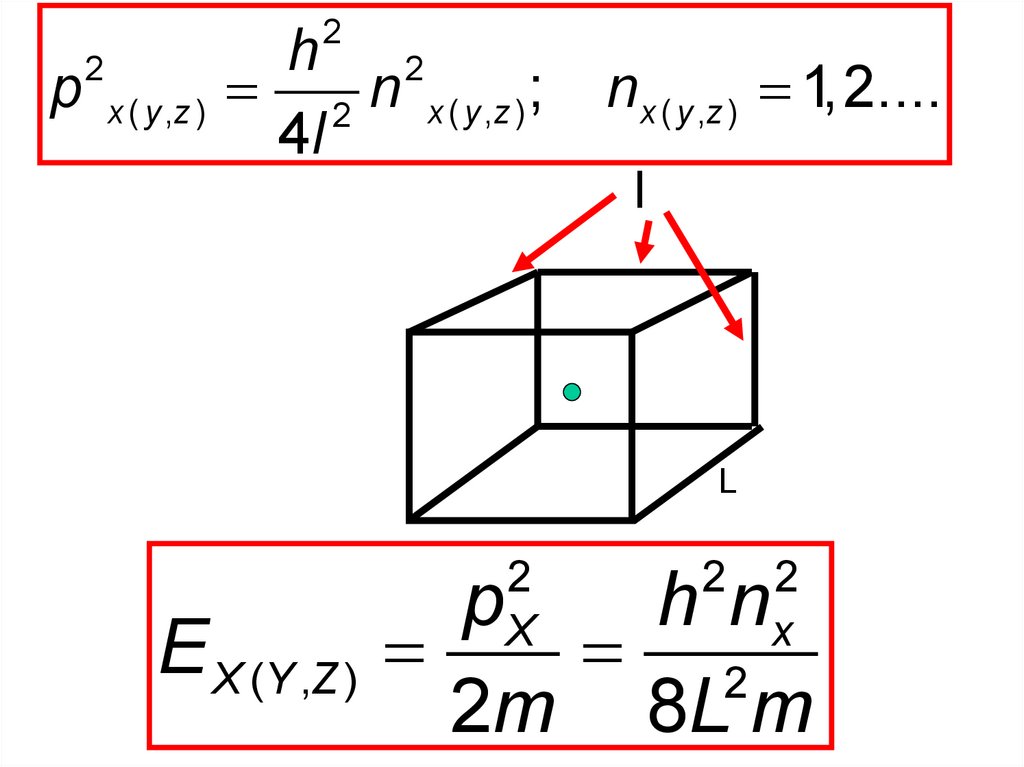
2p
2
x ( y ,z )
h 2
2 n x ( y ,z ) ;
4l
nx ( y ,z ) 1,2....
l
L
E X (Y ,Z )
2
X
2
2
x
p
hn
2
2m 8L m
44.
Квантовый расчет поступательной суммыh
h2
pi
n; i 2
n 2 ; n 1, 2......
2L
4 L 2m
Qi e
h2
2
n2
4 L 2 mkT
n 1
Qi e
0
h2
x2
2
4 L 2 mkT
1
dx
2
1/2
; gi 1
1/2
1 2mkT 4 L2
2
h2
2 mkT
L
2
h
V
3/2
2 mkT
3
Qпост QxQyQz
L
2
mkT
2
3
h
h
3/2
1/2
45.
Поступательная сумма (интеграл)Q
V 2 mkT
N! N!
h3 N
N
Z пост.
N
3N / 2
ln Z пост. N ln V N ln N N ln e N ln
2 mkT
h
3
3/ 2
2 mkT 3/ 2 Ve
N ln
3
hN
0
Fпост. Eпост
. kT ln Z пост.
2 mkT 3/ 2 Ve
RT ln
3
hN
46.
Поступательные вклады в т/д функции0
Fпост. Eпост
. kT ln Z пост.
S пост.
2 mkT 3/ 2 Ve
RT ln
3
h
N
(2 mkT )3/ 2Ve 3
(2 mkT )3/ 2Ve 3
1
F
RT R ln
R
R ln
3
3
Nh
T
Nh
T V
2
2
сv , пост.
3 1 3
S
T
RT R
2 T 2
T V
1 RT
F
p
RT
V
V
V T
47.
Формула Закура-Тетроде0
900
S
Дж
(Mg, газ )
моль К
900
0
тд
S
0
0
ст
S
c p ( тв )
T
dT S
0
газ тв
2 mkT
R ln
Nh
Sст
3
3
2
V
170.95
5
R 171.50
2
5
3
R lnT R ln M R ln p 9,677
2
2
48.
ЭЛЕКТРОННАЯ СУММА по СОСТОЯНИЯМ49.
Электронная сумма по состояниямQ g0
1
4
эл
~ 10
k
g1e
g0
g1
kT
T
50.
Электронная сумма по состояниямQэл gi e
i
Z эл QэлN ;
i
kT
e
0
kT
1 0
2 0
0
g 0 g1e kT g 2e kT ... g 0e kT
Fэл. E0, эл. Fэл. N 0, эл. kTN ln g 0
S эл kN ln g 0 ; cV , эл. 0
















































 Физика
Физика








