Электронная составляющая теплоемкости атомарного хлора. Лекция 21

1.

Лекция 21
Электронная составляющая теплоемкости атомарного
хлора.
µ - пространство. Распределение молекул по
скоростям и энергиям в идеальном газе. Средние
скорости, средние энергии.
Колебательные и вращательные суммы по состояниям
Внутреннее вращение.

2.

Лекция 20
Канонический ансамбль. Суммы по состояниям Z и Q.
Характеристическая температура.
Поступательная сумма по состояниям.
Электронная сумма по состояниям.

3.

1 балла
Микроканонический и канонический ансамбли.
Какое из утверждений верно?
1. В каноническом ансамбле больше микросостояний.
2. У микроканонического ансамбля меньше энергии.
3. В микроканоническом ансамбле энергия
одинакова во всех микросостояниях.
4. Внутренняя энергия системы – это максимальная
энергия в каноническом ансамбле.

4.

Интеграл по состояниям системы равен
Z e
E ( p,q)
kT
d
1 балла
А что такое E (p,q) ?
1.
Это сумма энергий частиц, входящих в систему
2.
Это энергия системы в различных
макросостояниях
3.
Это внутренняя энергия системы, U
4.
Это энергии системы в различных микросостояниях

5.

2 балла
В системе установилось равновесие Агаз + Вгаз = АВгаз.
Мы увеличиваем общее давление в системе. При этом
изменились парциальные давление р(А), р(В) и р(АВ).
Почему?
1. Изменили общее давление, должны измениться и
парциальные давления.
2. Изменилась константа равновесия, К
3. Газы перестали быть идеальными
4. Правильно (1) и (2)
5. Правильно (1) и (3)

6.

Энтропия в каноническом ансамбле.
Найдите правильную формулу:
1.
S k ln f ( E )
2.
S k ln ( p, q )
3.
S k ln ( p, q)
4.
S k ln ( p, q)
1 балла

7.

Характеристическая температура, θ.
Найдите правильное утверждение.
1 балла
1. Характеризует фазовое состояние системы
2. Всегда больше комнатной температуры
3. Характеризует расстояние между уровнями энергии
4. Характеризует расстояние между уровнями
энергии, в джоулях !
5. Самая высокая поступательная температура –
у поступательной энергии.

8.

В системе А-В установилось фазовое равновесие жидкий
раствор-пар и все химические равновесия. В паре
обнаружены молекулы А, В, АВ и А2В.
Сколько компонентов в системе?
2 балла
1. 2 компонента
2. 4 компонента
3. В паре 4 компонента, а в жидкости - 2 компонента.
4. 4 компонента, если пар идеальный газ
5. 4 компонента, если жидкость – идеальный раствор.

9.

СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА.
Метод ячеек Больцмана и Канонический ансамбль Гиббса

10.

Метод ячеек
Канонический ансамбль
S k ln W
Wmax
S k ln k ln ( E )
N!
n1 ! n2 !...ni !
i
k ln ( E ) k ln ( E )
i
N kT ni
1 kT
ni e ; i e
Q
N
Q
Q qi e
i
i
kT
1
E p, q e
Z
Z e
E p ,q
kT
E p ,q
kT
zi e
i
Ei p ,q
kT

11.

«Принцип max” в каноническом ансамбле?
Да, есть!
Метод ячеек
ni N
Канонический ансамбль
i
n
i i
E
i
i 1
( E )
E ( p, q ) E
ln W max
k ln k ln max
Метод Лагранжа
Метод Лагранжа
1 kT i
i e
Q
1 E (kTp ,q )
E ( p, q ) e
Z

12.

СТАТИСТИЧЕСКАЯ ТЕРМОДИНАМИКА.
ЧТО МЫ УЖЕ ЗНАЕМ?

13.

Описание равновесного состояния в стат. термодинамике
S k ln W , W количество микросостояний системы
Фазовое пространство, W ; E ( p, q )
1
Канонический ансамбль, E ( p, q ) e
Z
E ( p,q)
kT
S k ln E ( p, q ) ; F kT ln Z , в каноническом ансамбле
Сумма по состояниям, Z zie
i
QN
Идеальный газ, Z
N!
Ei ( p ,q )
kT

14.

Идеальный газ независимость пост. , кол. , вр. , эл. , яд.
Qпост. Qкол. Qвр. Qэл. Qяд.
Q
Z
N!
N!
N
Qпост.
2 mkT
h
3
3/2
V
N
Qэл. g 0
Qкол. ; Qвр. ; Qяд. ??

15.

Формула Закура – Тетроде.

16.

Формула Закура-Тетроде
0
900
S
Дж
(Mg, газ )
моль К
900
0
тд
S
0
Sст,пост
c p ( тв )
T
2 балла
dT S
0
газ тв
2 mkT
R ln
Nh
3
2
3
3
сv ,пост. R
2
V
170.95
5
R 171.50
2

17.

Формула Закура-Тетроде
Sст
2 mkT
R ln
Sст
Nh
3
3
2
V
5
R 171.50
2
5
3
R lnT R ln M R ln p 9,677
2
2
S {Дж моль-1 K-1}, T{K}, M {у.e.}, p{бар}

18.

ЭЛЕКТРОННЫЕ СУММЫ по СОСТОЯНИЯМ
Характеристические температуры

19.

Характеристическая температура
;
k
k
(4)
1
(1)
1
3
1 10 K
3
2
2 10 K 104 K
3
8

20.

Характеристическая температура
i 1 i e
i 1
kT
e
i
kT
i 1 i
kT
kT
e e
1
i
i
kT
T
e e 1 0 при T
i 1 i
k

21.

Суммирование? Интегрирование?
Q ;
T
Q ; T
Q qo ;
T

22.

Электронная сумма по состояниям
Q g0
1
4
эл
~ 10
k
g1e
g0
g1
kT
T

23.

Электронная сумма по состояниям
Qэл gi e
i
Z эл QэлN ;
i
kT
e
0
kT
1 0
2 0
0
g 0 g1e kT g 2e kT ... g 0e kT
Fэл. E0, эл. Fэл. N 0, эл. kTN ln g 0
S эл kN ln g 0 ; cV , эл. 0

24.

Вырожденности основного электронного уровня
g0
Атом
H
He
Li
Be
B
C
N
O
2
1
2
1
2
1
4
5

25.

СV
Дж
моль * К
CV (Cl ) ??
14.39
3/2R
3
Cv ,пост. R 12.471
2
700 K
T

26.

Теплоемкость Сl
Qэл gi e
i
Fэл N эл ,0
эл ,i
kT
e
эл ,0
kT
gie
эл ,i
kT
e
эл ,0
kT
i
эл ,1
kT
g 0 g1e
2
эл ,1
F
kT
kTN ln g 0 g1e
, cv T 2
T V
g 0 2; g1 4

27.

μ – пространство. Система, состоящая
из одной частицы
- пространство размерности 6.

28.

Пространство Ω
E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...)
3 N импульсов p , 3 N координат (q )
1 E (kTp ,q )
E ( p, q e
Z
Пространство μ
N 1; ( p1, x , p1, y , p1, z ; q1, x , q1, y , q1, z )
3 импульсa p , 3 координаты (q )
( p, q
1
Qпост.
e
пост . ( p ,q )
kT

29.

Плотность вероятности в μ-пространстве
( p, q
1
Qпост.
d p ( p, q )
e
пост . ( p , q )
kT
h
e
3/ 2
(2 mkT ) V
dpx dp y dpz dqx dq y dqz
q
h
3
3
3
h
V
e
3/ 2
3
(2 mkT ) V h
1
d ( p ) p dpx dp y dpz
e
3/ 2
(2 mkT )
px2 p 2y pz2
3
2 kTm
px2 p 2y pz2
2 kTm
dpx dp y dpz
px2 p 2y pz2
2 kTm
m
d (V ) V dvx dv y dvz
e
3/ 2
(2 mkT )
dpx dp y dpz
m vx2 v 2y vz2
2 kT
dvx dv y dvz

30.

dVx dVy dVz V dVd sin d
2
2
d sin d V
0
0
Vz
V
θ
Vy
Vx
ψ
2
dV 4 V dV
2

31.

Распределение по скоростям и по модулю скорости
1
d ( p) p
e
3/ 2
(2 mkT )
px2 p 2y pz2
2 kTm
dpx dp y dpz
3
m
d (V ) V dvx dv y dvz
e
3/ 2
(2 mkT )
3
m
d (V ) V dV
e
3/ 2
(2 mkT )
mV 2
2 kT
m vx2 v 2y vz2
2 kT
4 V 2 dV
dvx dv y dvz

32.

Распределение Максвелла
dnV
V dV 4
n
m
3
(2 mkT )
3
2
e
mV 2
2 kT
V dV
ρV
dnV
n
dV
2
V

33.

Как Максвелл получил свое распределение?
v
1.
dw(v) dw(v)
v
2.
vy
vz
dw(vx ) f (v y ; vz )
vx
dw(v y ) f (vx ; vz )
dw(vz ) f (v y ; vx )

34.

Средний модуль скорости.
/V / V V dV
4 m
0
4 m
3
(2 mkT )
3
2
e
mV 2
2 kT
3
V dV
1 4 m 4( kT )
3
3
2
2
a
2
2
2
(2 mkT )
(2 mkT ) 2m
3
m 1 2(kT )2
a
; 2
2kT 2a
m2
3
8kT
m
2
1
2

35.

T=298 K
8kT
v
m
1
2

36.

Распределение Максвелла при разных температурах
ρV
T1
T2 > T1
T2
VT1
8kT
V
m
VT2
V
1
2

37.

Распределение по энергиям молекул в μ-пространстве
3
m
d (V ) V dV
e
3/ 2
(2 mkT )
V2
2
;
m
d
m
1
2VdV ; dV
d
2
mV
mV 2
2 kT
4 V 2 dV
1
2
m
m
1/ 2
d
m3
2
1
kT
d ( ) d
e
4
d
1/ 2
3/ 2
1/ 2
(2 mkT )
m m 2
2
1/ 2
kT
d ( ) f d 1/ 2
e 2 d
3/ 2
(kT )

38.

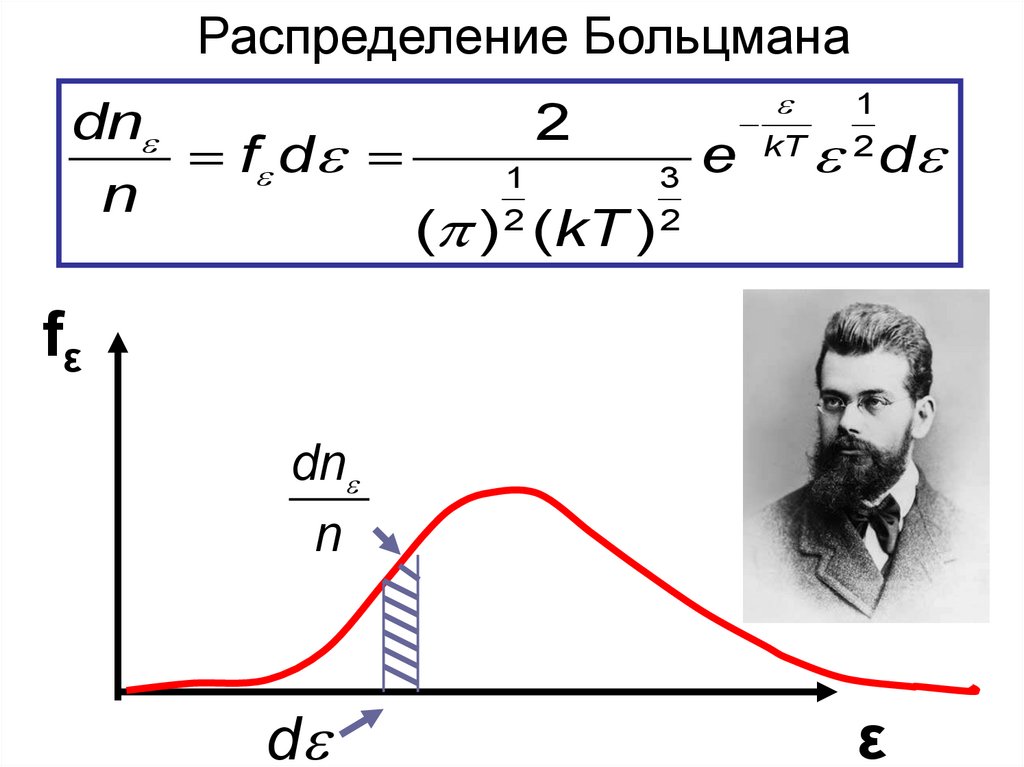
Распределение Больцмана
dn
f d
n
2
1
2
( ) ( kT )
3
2
e
kT
1
2
d
fε
dn
n
d
ε

39.

Средняя энергия
f d
0
fε
0
e
3
2
d
2
( ) ( kT )
3
4
0
dn
n
d
1
2
3
2
e
kT
3
2
d
1
2
5
2
3
kT
2
ε

40.

d
f (E ) (E ( p, q ))
dE
(E ( p, q ) ~ e
E
kT
d (E )
~E
dE
Eср
3N
1
2
E

41.

Плотность вероятности fE в Г- и μ- пространстве
1
e
Z
fE
E
kT
d
dE
~E
~
3
N 1
2
1
2
1 kT d
e
Q
d
E N
E,ε

42.

Сумма по состояниям для колебательного движения

43.

Характеристическая температура
;
k
k
(4)
1
(1)
1
3
1 10 K
3
2
2 10 K 104 K
3
8

44.

Суммирование? Интегрирование?
Q ;
T
Q ; T
Q qo ;
T

45.

Двухатомная молекула

46.

Гармонический осциллятор
f
m
M
R
f – константа упругости.
1
2
1/2
f
m M
M m
2
f 2 p
E ( p, q ) q
2
2

47.

Уровни колебательной энергии
1
E (v) h , 0,1, 2.....
2
h
h
2
h
кол
~ 500 5000 K
k
( N 2 ) 3340 K

48.

Колебательная сумма по состояниям 2-х атомной молекулы
Qкол.,1
hv ( 1/ 2)
e
e
0
hv
1
1 e kT
Qкол.
kT
hv1
2 kT
hv
2 hv1
1
kT
kT
1 e
e
.......
1 e
2 hv1
hv1 1
kT
kT
e
.......
1 e
hv1
1 e kT
e
0
hv
1
kT
hv ( 1/ 2)
1
kT
e
hv
1
2 kT
1
hv
1
1 e kT
1
; Z кол. Qкол. N

49.

Колебательная сумма Zкол и термодинамические функции
ln Z кол
h 1
N ln Q1 N
N ln 1 e
2kT
h 1
kT
h
h
1
1
1
h
0
Fкол E 0,* RT 1 RT ln 1 e kT Eкол
RT 1 e kT
2
kT
h 1
kT
кол ,1
кол ,1
e
e T
h 1
сv ,1 R
R
2
2
h 1
кол ,1
kT
T
T
kT
1
e 1
e
2
2

50.

Е
Уровни отсчета энергии
0
Екол
i
h i
2
Уровень нулевых квантовых чисел =
Энергия системы при Т= 0 К
Е
0,*
Е
0
r

51.

Колебательная теплоемкость. Одно колебание.
cV R кол exp кол exp кол 1
T
T T
2
cV
R
2
сV 0, T 0; cv R, T
кол
T
T 0
T

52.

N- атомная молекула
Число нормальных колебаний, i :
Линейная молекула:
i = 3N - 5
Нелинейная молекула:
i = 3N - 6

53.

Колебательная сумма Zкол и термодинамические функции
ln Z кол
Fкол E 0,*
h i
h i
kT
N ln Qi N
N ln 1 e
i 2 kT
i
i
h
i
h i
1
RT
RT ln 1 e kT
2
i kT
i
h i
kT
h
i
0
Eкол RT ln 1 e kT
i
кол ,i
кол ,i
e
e T
h i
сv ,i R
R
2
2
h i
кол ,i
kT
T
kT
T
1
1
e
e
2
2
сv cv ,i
i

54.

Колебательная теплоемкость, NH3, 1000K
кол,i
кол,i кол ,i
cV сv ,i R
exp
exp
1
i 1
T
T T
2
6
cV
0.87R (950)
R
3336,68 см–1 , 950,42 см–1 ,
3443,47 см–1(2) и 1627,75 см–1(2)
0.18R (3443)
1.4
T
2
4.9
T 0
кол
T

55.

Вращательная и ядерная суммы по состояниям.

56.

Характеристическая температура
;
k
k
(4)
1
(1)
1
3
1 10 K
3
2
2 10 K 104 K
3
8

57.

Суммирование? Интегрирование?
Q ;
T
Q ; T
Q qo ;
T

58.

Двухатомная молекула. Момент инерции.
rM
rm
m
M
R rM rm
R
MrM mrm
m M
M m
I Mr mr R
2
M
2
m
2

59.

Двухатомная молекула. Вращательное движение
M M M
I
M
вр
2
2I
2I
2
Qвр e
2
2
x
2
y
2
z
M x2 M y2 M z2
2 I kT
dM x dM y dM z
М I угловой импульс, не масса !

60.

Уровни вращательной энергии
вр
h
2
8 I
2
J ( J 1),
g вр 2 J 1
J=2
gвр= 5
J=1
gвр = 3
J=0
вр
gвр = 1
J 0,1,2....
h
2
8 Ik
2
~ 0.05 85 K
6(h /8 I )
2
2
2(h / 8 I )
0
2
2

61.

Вращательная сумма двухатомной молекулы
Qвр. (2 J 1) e
h2
8 2 IkT
J ( J 1)
;
J 0
Q
(2 J 1) e
вр
T
J ( J 1)
dJ
J 0
Qвр e
ax
вр
T
J ( J 1)
d J ( J 1 )
J 0
Переменная : х J J 1 ;
e
вр.
h2
2
8 Ik
dx d J J 1 2 J 1 dJ
dx a e
1
0
8 IkT
T
Qвр.
2
h
вр.
ax
1
I a
0
a
T
вр
2
Z вр Qвр N
вр
T

62.

Вращательная сумма двухатомной молекулы
(2 J 1) e
вр
T
J J 1
J
e
T
y
0
(2 J 1) e
вр
T
J J 1
J
вр
вр
T,
2 J 1 e
J
вр
T
1 1 вр
dy
3 15 T
T
вр
J ( J 1)
1 1 вр
3 15 T
1 3e
2
вр
T
....

63.

Вращательная сумма двухатомной молекулы.
Вклад в термодинамические функции.
F E0 kT ln Z вр kNT ln Qвр kNT ln
F
сv T 2 Nk R
T V
2
2
T
вр

64.

Вращательная сумма для многоатомной молекулы.
Нелинейная молекула:
1
2
Qвр
2
8
I X kT
h
1
2
2
8
IY kT
1
2
h
Линейная молекула:
Qвр
2
8
IkT
h2
число симметрий
2
8
I Z kT
h
1
2

65.

Вращательная сумма для многоатомной молекулы.
Вклад в термодинамические функции
Нелинейная молекула:
Fвр E0 kNT ln Qвр RT ln
1
2
8
2
3
2
kT I X IY I Z
h3
1
2
; cv
Линейная молекула:
Fвр E0 kNT RT ln
2
8
IkT
число симметрий
h
2
; cv R
3
R
2

66.

Внутреннее вращение

67.

H
H
H
C
C
H
H
H
φ = π/3
φ=0
E0
E 1 cos3
2
E0
0
π/3
2π/3
φ

68.

Сумма по состоянию для внутреннего вращения
Qвв
2 I вв kT
h
1
2
2
e
E0
1 cos 3
2 kT
d
0
8 I вв kT
E0 0, 2 , Qвв
h
0
2
1
2
2
1
2
Число степеней свободы: 3 пост. +3(2) вр. +вв. +(3N-6(5)-вв.) кол. =3N

69.

Ядерные и вращательные суммы по состоянию

70.

Ядерные суммы по состояниям
Для атома:
Qяд g0, яд
Fяд E0 RT ln g0, яд ; S яд R ln g0, яд ; cv 0
Для молекулы:
Qяд g0,i , яд ,
Fяд E0 RT ln g0,i , яд ; S яд R ln g0,i , яд ; cv, яд 0
i
i
i
Для химической реакции:
gi (продукты)
gi (продукты)
0; S R ln i
0
Fяд RT ln i
яд
gi ( реагенты)
gi ( реагенты)
i
i

71.

Вырожденности основных ядерных уровней атомов
Элемент
p
n0
gяд
H
1
0
2
Ne
10
10
1
K
17
20
9
Cl
23
27
4
g яд Н 2 22 4

72.

Вращательная и ядерная суммы
гомоядерной двухатомной молекулы А2
пост. кол. эл. яд. вр.
Для молекулы из ядер с нечетной массой :
пост. кол. эл. яд. вр.
яд. ( ) вр. ( ); яд. ( ) вр. ( )
вр. если J нечетно; вр. если J четно;

73.

Вращательная и ядерная суммы
гомоядерной двухатомной молекулы H2
QядQвр g яд as Qвр s , чт. J g яд s Qвр as , нчт. J
1
T
Qвр Qвр чт Qвр нчт
2
2 вр
gяд (s)= 3
gяд (as) = 1
(-)Ψяд
(+) Ψяд
Орто- Н2
Вр. уровни
Пара- Н2

74.

Вращательная и ядерная суммы
гомоядерной двухатомной молекулы А2
пост. кол. эл. яд. вр.
яд. ( ) вр. ( ); яд. ( ) вр. ( )
Qпара
Qорто
1 Qврч Qпост. Qкол. Qэл.
1
3 Qврнчт Qпост. Qкол. Qэл. 3
Fвр. E 0 kNT ln Qвр kNT ln
T
вр
Fвр E 0 kNT ln Qвр kNT ln
; cV R
T
; cv R;
2 вр
( АВ)
A2

75.

Вращательная теплоемкость Н2
cV
Пара – Н2 (ас)
Q( s,чет. ) 1 5e
6
вр
T
...
R
300 К
H2
Орто – Н2 (с)
Q(аs,неч. ) 3e
2
вр
T
7e
12
вр
T
....
T

76.

Пара- и орто-водород при низких температурах.
Qвр. (2 J 1) e
h2
8 2 IkT
J ( J 1)
;
J 0
вр.
h
8 Ik
Пара- Н2
Qврч 1 5e
6 h2
8 2 I kT
.....( J 0, 2,....)
Орто- Н2
Qврнч 3e
2 h2
8 I kT
2
7e
12 h 2
8 2 I kT
2
.....( J 1,3,......)
2

77.

Энтропия НСl, S0298K,эксп. = 186,6 {Дж/моль/град}
S
0
пост элек .
2 mkT
R ln
h3 N
3
2
V
5
R R ln z0 153,5
2
2
8
I kT
1
Sвр R ln
R 33,1
2
h
h i hkT 1
e
1
6
kT
6,7 10
Sкол R ln
R
h 1
h i
kT
kT
1 e
1 e