Похожие презентации:
Теории теплоемкости Эйнштейна и Дебая (без вывода). Лекция 22
1.
Лекция 22Теории теплоемкости Эйнштейна и Дебая (без вывода).
Вращательная и ядерная суммы по состояниям.щат
2.
Лекция 21μ- пространство. Распределения Максвелла по скоростям
и Больцмана по энергиям.
Колебательные и вращательные суммы по состояниям.
3.
Энтропия в каноническом ансамбле.Найдите правильную формулу:
1.
S k ln f ( E )
2.
S k ln ( p, q )
3.
S k ln ( p, q)
4.
S k ln ( p, q)
1 балла
4.
Характеристическая температура, θ.Найдите правильное утверждение.
1 балла
1. Характеризует фазовое состояние системы
2. Всегда больше комнатной температуры
3. Характеризует расстояние между уровнями энергии
4. Характеризует расстояние между уровнями
энергии, в джоулях !
5. Самая высокая поступательная температура –
у поступательной энергии.
5.
В системе А-В установилось фазовое равновесие жидкийраствор-пар и все химические равновесия. В паре
обнаружены молекулы А, В, АВ и А2В.
Сколько компонентов в системе?
2 балла
1. 2 компонента
2. 4 компонента
3. В паре 4 компонента, а в жидкости - 2 компонента.
4. 4 компонента, если пар идеальный газ
5. 4 компонента, если жидкость – идеальный раствор.
6.
Число компонентов системы – это минимальноечисло независимых химических частиц, которое
необходимо для описания состава всех фаз системы.
Дополнительные химические равновесия уменьшают
число компонентов. (IUPAC)
AB A B ; A B 2 A B ?
2
жд
nAB
d AB nAжд
d A2B 0
2B
(T , p const )
n d ln p AB n d ln p A2B 0 (T , p const )
жд
AB
жд
A2 B
жд
жд
жд
nAB
2nBжд nAжд ; nAжд
n
n
A
B
2B
7.
Средняя кинетическая энергия и средняя скоростьмолекул в идеальном газе.
Найдите верные утверждения!
1 балла
1.
Значительная доля молекул имеет энергию выше
средней
2.
Средняя скорость растет с увеличением массы
3.
Средняя энергия растет с увеличением массы
4.
ср
m V
2
2
8.
Для расчета суммы по состояниям Q существуютформулы (1) и (2)
Q e
kТ
dpdq (1),
Q zi e
i
kT
1 балла
(2)
i
которой из них нужно пользоваться?
1. нужно воспользоваться формулой (1)
2. можно воспользоваться формулой (2), но лучше –
формулой (1)
3. иногда верна формула (1), а иногда – формула (2)
4. формула (2) верна всегда, а формула (1) – только в
особых случаях
9.
Чем мембранное равновесие отличается от фазового?Найдите верные утверждения!
2 балла
При мембранном равновесии :
1. Не во всех фазах температура одинакова.
2. Не во всех фазах давление одинаково.
3. Не во всех фазах энтропия смешения одинакова.
4. Не во всех фазах работает уравнение
Менделеева Клапейрона.
5. Не во всех фазах работает уравнение Гиббса Дюгема
10.
Идеальный газ независимость пост. , кол. , вр. , эл. , яд.Qпост. Qкол. Qвр. Qэл. Qяд.
Q
Z
N!
N!
N
Qпост.
Qi ,кол.
2 mkT
h
0
kT
V
Qэл. g 0
3
hvi ( 1/2)
e
3/2
e
hvi
2 kT
N
1
hv
i
1 e kT
1
3 N 6
; Qкол. Qi ,кол.
i
Qвр. ; Qяд. ??
11.
Сумма по состояниям для колебательного движения12.
Уровни колебательной энергии1
E (v) h , 0,1, 2.....
2
h
h
2
h
кол
~ 500 5000 K
k
( N 2 ) 3340 K
13.
Колебательная сумма по состояниям 2-х атомной молекулыQкол.,1
hv ( 1/ 2)
e
e
0
hv
1
1 e kT
Qкол.
kT
hv1
2 kT
hv
2 hv1
1
kT
kT
1 e
e
.......
1 e
2 hv1
hv1 1
kT
kT
e
.......
1 e
hv1
1 e kT
e
0
hv
1
kT
hv ( 1/ 2)
1
kT
e
hv
1
2 kT
1
hv
1
1 e kT
1
; Z кол. Qкол. N
14.
Колебательная сумма Zкол и термодинамические функцииln Z кол
h 1
h 1
kT
N ln Q1 N
N ln 1 e
2kT
h 1
kT
кол ,1
кол ,1
e
e T
h 1
сv ,1 R
R
2
2
h 1
кол ,1
kT
T
T
kT
1
e 1
e
2
2
15.
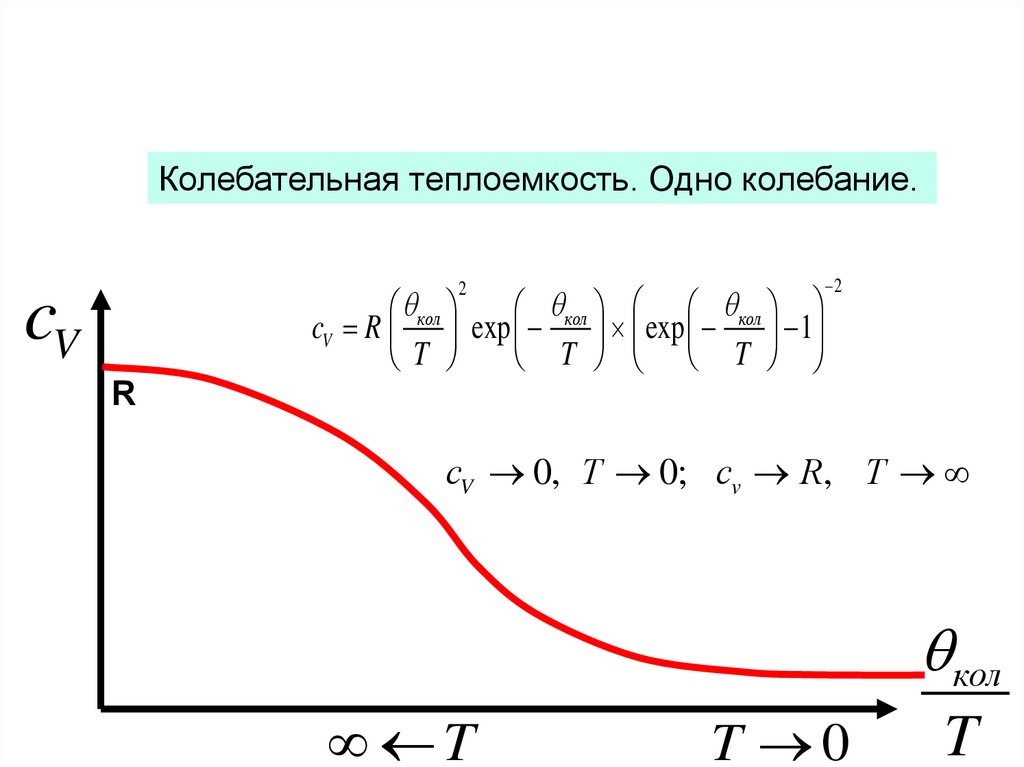
Колебательная теплоемкость. Одно колебание.кол
кол кол
cV R exp
exp
1
T
T T
2
cV
2
R
сV 0, T 0; cv R, T
кол
T
T 0
T
16.
Статистический расчет теплоемкости кристаллов(атомных кристаллов).
17.
E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) 1 ( p1, x ; q1, x ... p1, z ; q1, z ..)... i ( pi , x ; qi , x ... pi , z ; qi , z ..) .. N ( pN , x ; qN , x ... pN , z ; qN , z ...)
E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) E ( p1, x ;.. pi , y ... pN , z ) E (q1, x ..; qi , y ...qN , z ...)
E ( p1, x ; q1, x .. pi , y ; qi , y ... pN , z ; qN , z ...) Eкол.
18.
F- U0 = -kT ln ZколU0 = Eпот
19.
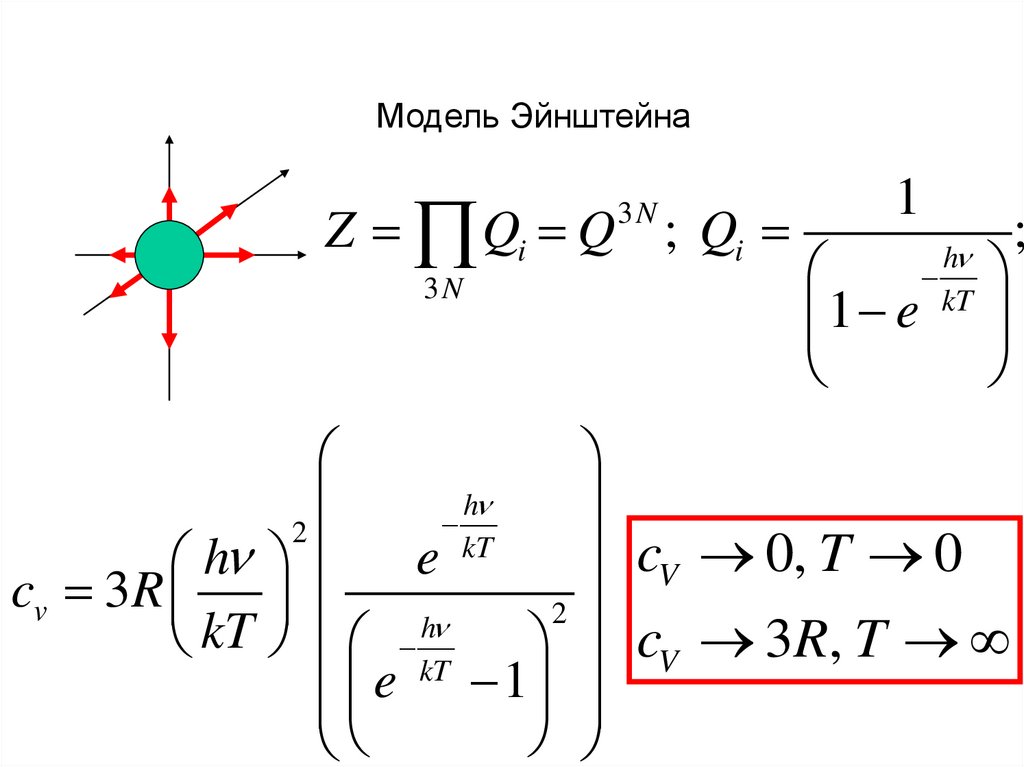
Модель ЭйнштейнаZ Qi Q ; Qi
3N
3N
1
h
kT
1
e
h
2
kT
h
e
cV 0, T 0
cv 3R
2
h
kT kT
cV 3R, T
e 1
;
20.
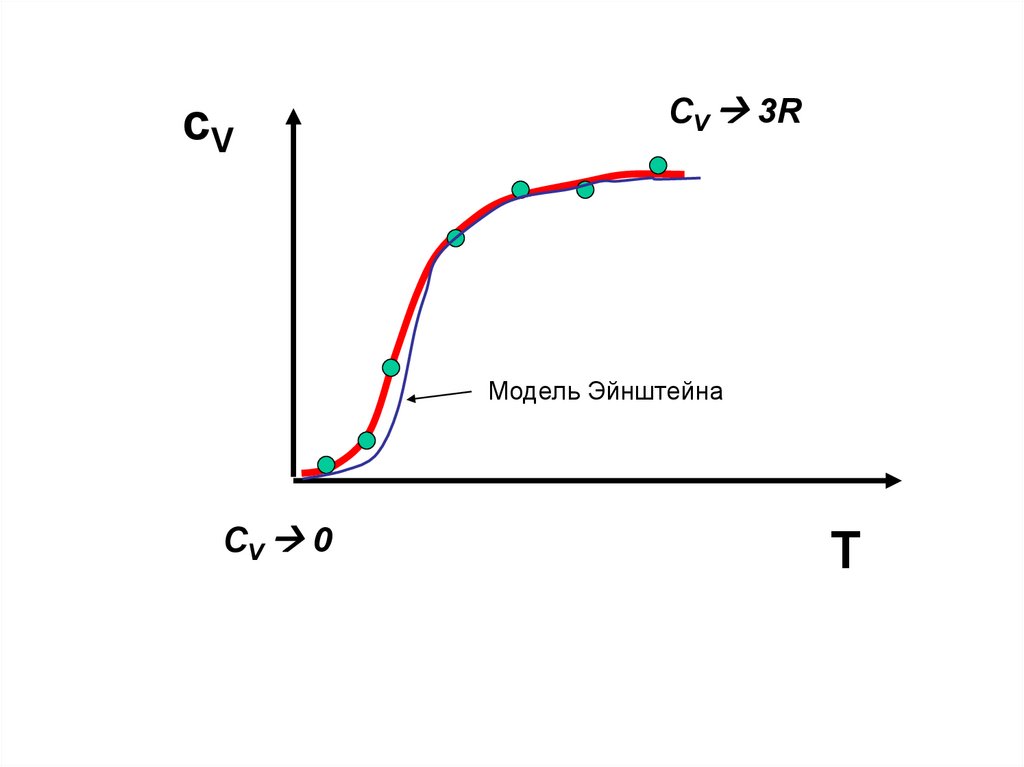
сVСV 3R
Модель Эйнштейна
СV 0
T
21.
Модель Дебая22.
Модели Дебая и Эйнштейна.Обе модели позволяют рассчитать теплоемкость кристаллов
Обе модели рассчитывают энергию кристалла E как
колебательную энергию решетки.
Модель Эйнштейна предполагает, что все N атомов в
решетке совершают нормальные колебания (всего 3N
колебаний) с одинаковой частотой, ν . Модель
не дает способа расчета этой частоты.
В модели Дебая кристалл рассматривается как непрерывная
однородная упругая среда. Существует непрерывный
набор частот колебаний (от 0 до νmax). Для частот колебаний
есть функция плотности вероятности. Модель Дебая дает
способ расчета частот колебаний в решетке.
23.
Модель Дебая0 max ;
max
2
q 9 N 3
max
1
3
3N
cзвука ;
4 V
h
i
ln Z i ln 1 e kT
Дебая
;
2
dw( ) 9 N 3
max
d
1
3
h max h 3 N
cзвука
k
k 4 V
max
1
; ln Z 3 N q ln
h i
0
1 e kT
ln Z
2
2 ln Z
F E0 kT ln Z ; cV 2kT
kT
2
T
T
V
V
d
24.
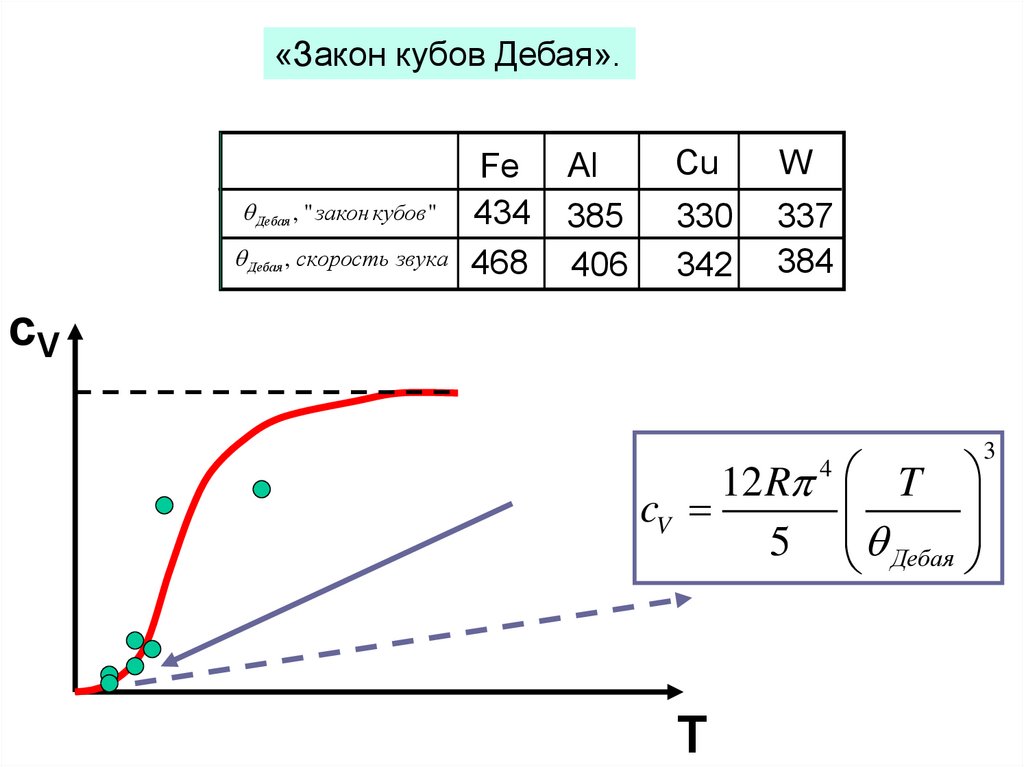
«Закон кубов Дебая».Дебая , " закон кубов "
Дебая , скорость звука
Fe
434
468
Al
385
406
Cu
W
330
342
337
384
сV
12 R
cV
5
T
4
T
Дебая
3
25.
Поиски новых способов оценки теплоемкости кристалловh i
2
2,3
kT
h
e
i
cv 3R
2
h
kT i
i
kT
e 1
26.
Теплоемкость молекулярных кристалловсv cV ( реш.) сV ( мол.)
27.
Вращательная и ядерная суммы по состояниям.28.
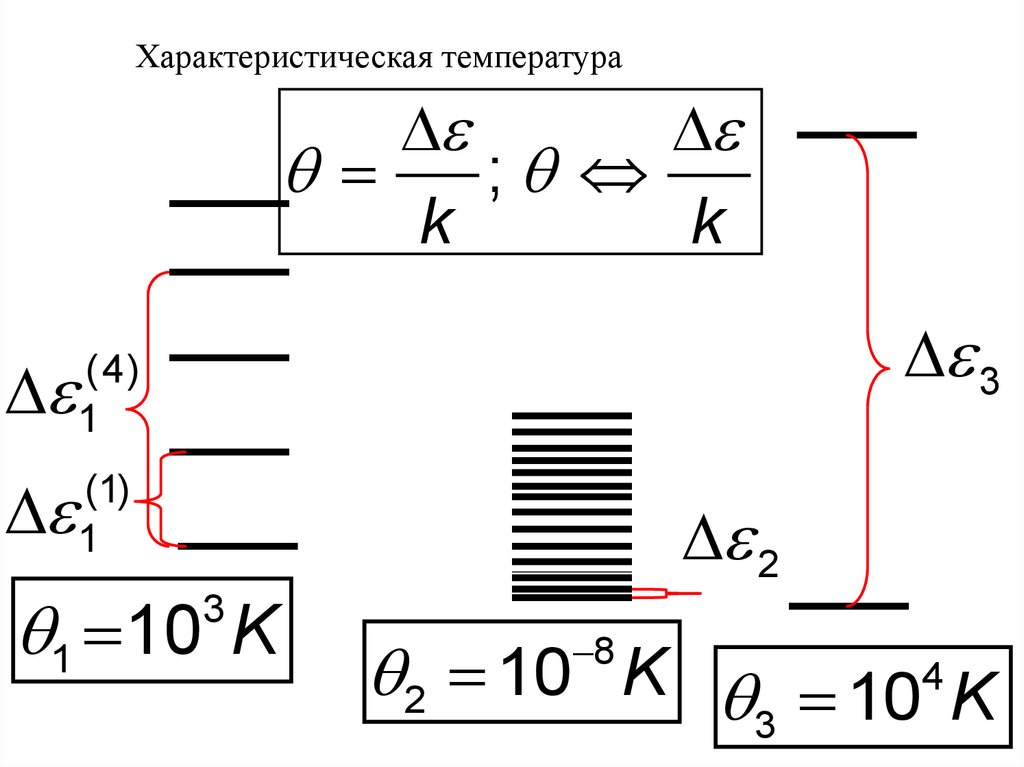
Характеристическая температура;
k
k
(4)
1
(1)
1
3
1 10 K
3
2
2 10 K 104 K
3
8
29.
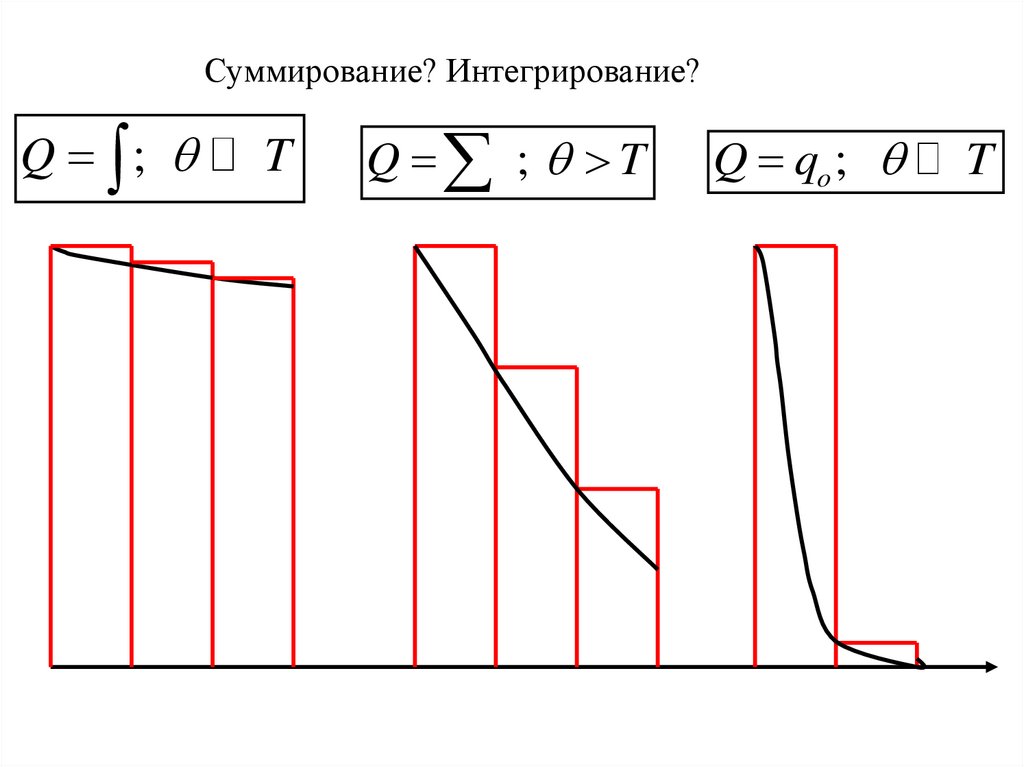
Суммирование? Интегрирование?Q ;
T
Q ; T
Q qo ;
T
30.
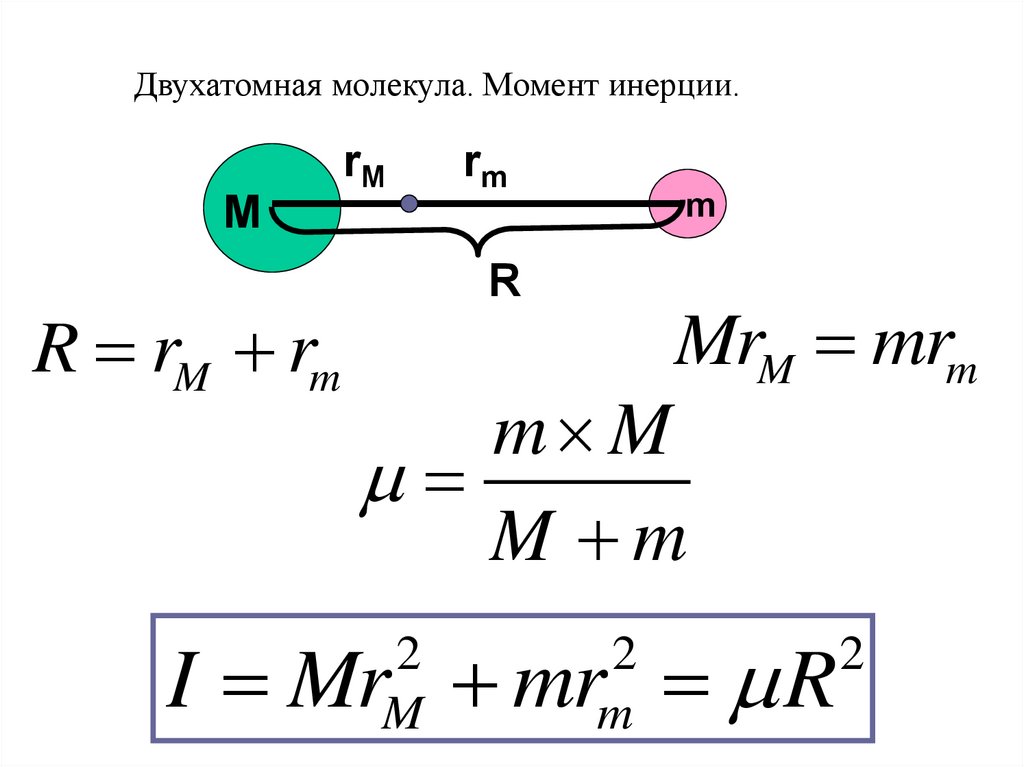
Двухатомная молекула. Момент инерции.rM
rm
m
M
R rM rm
R
MrM mrm
m M
M m
I Mr mr R
2
M
2
m
2
31.
Двухатомная молекула. Вращательное движениеM M M
I
M
вр
2
2I
2I
2
Qвр e
2
2
x
2
y
2
z
M x2 M y2 M z2
2 I kT
dM x dM y dM z
М I угловой импульс, не масса !
32.
Уровни вращательной энергиивр
h
2
8 I
2
J ( J 1),
g вр 2 J 1
J=2
gвр= 5
J=1
gвр = 3
J=0
вр
gвр = 1
J 0,1,2....
h
2
8 Ik
2
~ 0.05 85 K
6(h /8 I )
2
2
2(h / 8 I )
0
2
2
33.
Вращательная сумма двухатомной молекулыQвр. (2 J 1) e
h2
8 2 IkT
J ( J 1)
;
J 0
Q
(2 J 1) e
вр
T
J ( J 1)
dJ
J 0
Qвр e
ax
вр
T
J ( J 1)
d J ( J 1 )
J 0
Переменная : х J J 1 ;
e
вр.
h2
2
8 Ik
dx d J J 1 2 J 1 dJ
dx a e
1
0
8 IkT
T
Qвр.
2
h
вр.
ax
1
I a
0
a
T
вр
2
Z вр Qвр N
вр
T
34.
Вращательная сумма двухатомной молекулы(2 J 1) e
вр
T
J J 1
J
e
T
y
0
(2 J 1) e
вр
T
J J 1
J
вр
вр
T,
2 J 1 e
J
вр
T
1 1 вр
dy
3 15 T
T
вр
J ( J 1)
1 1 вр
3 15 T
1 3e
2
вр
T
....
35.
Вращательная сумма двухатомной молекулы.Вклад в термодинамические функции.
F E0 kT ln Z вр kNT ln Qвр kNT ln
2
F
2
сv T 2 Nk R
T V
T
вр
36.
Вращательная сумма для многоатомной молекулы.Нелинейная молекула:
1
2
Qвр
8
2
I X kT
1
2
h
8
Линейная молекула:
Qвр
2
IY kT
1
2
h
8
2
8
IkT
h2
число симметрий
2
I Z kT
h
1
2
37.
Вращательная сумма для многоатомной молекулы.Вклад в термодинамические функции
Нелинейная молекула:
Fвр E0 kNT ln Qвр RT ln
1
2
8
Линейная молекула:
Fвр E0 kNT RT ln
2
3
2
kT I X IY I Z
h3
2
8
IkT
число симметрий
h
2
1
2
3
; cv R
2
; cv R
38.
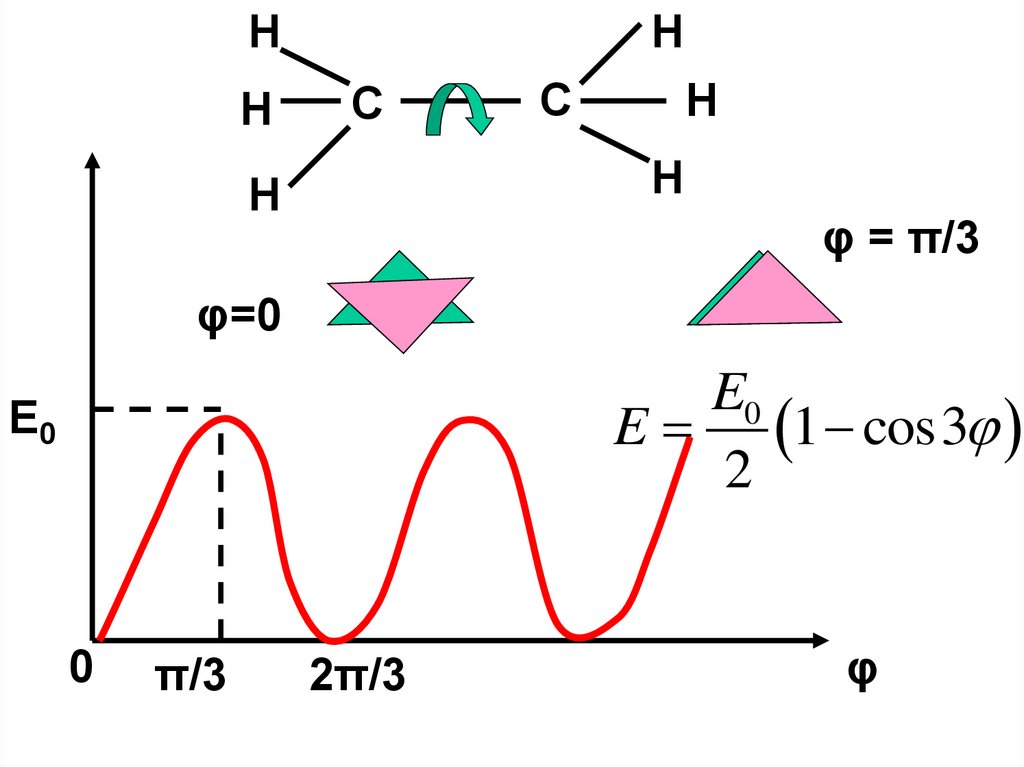
Внутреннее вращение39.
HH
H
C
C
H
H
H
φ = π/3
φ=0
E0
E 1 cos3
2
E0
0
π/3
2π/3
φ
40.
Сумма по состоянию для внутреннего вращенияQвв
2 I вв kT
h
1
2
2
e
E0
1 cos 3
2 kT
d
0
8 I вв kT
E0 0, 2 , Qвв
h
0
2
1
2
2
1
2
Число степеней свободы: 3 пост. +3(2) вр. +вв. +(3N-6(5)-вв.) кол. =3N
41.
Ядерные и вращательные суммы по состоянию42.
Ядерные суммы по состояниямДля атома:
Qяд g0, яд
Fяд E0 RT ln g0, яд ; S яд R ln g0, яд ; cv 0
Для молекулы:
Qяд g0,i , яд ,
Fяд E0 RT ln g0,i , яд ; S яд R ln g0,i , яд ; cv, яд 0
i
i
i
Для химической реакции:
gi (продукты)
gi (продукты)
0; S R ln i
0
Fяд RT ln i
яд
gi ( реагенты)
gi ( реагенты)
i
i
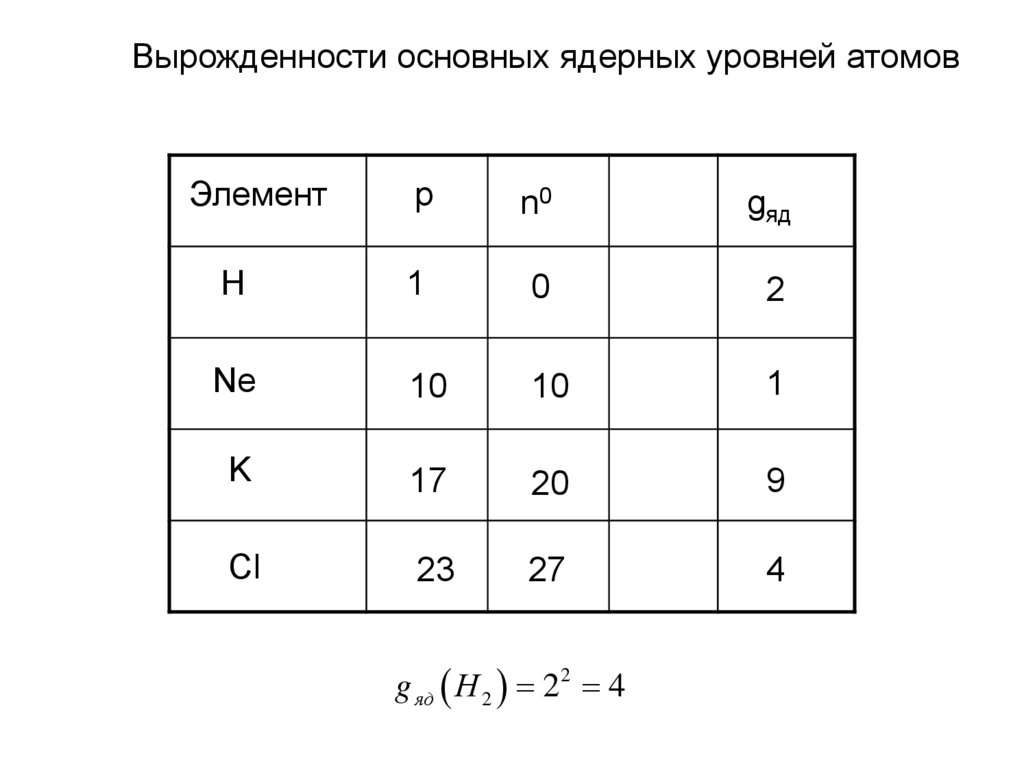
43.
Вырожденности основных ядерных уровней атомовЭлемент
p
n0
gяд
H
1
0
2
Ne
10
10
1
K
17
20
9
Cl
23
27
4
g яд Н 2 22 4
44.
Вращательная и ядерная суммыгомоядерной двухатомной молекулы А2
пост. кол. эл. яд. вр.
Для молекулы из ядер с нечетной массой :
пост. кол. эл. яд. вр.
яд. ( ) вр. ( ); яд. ( ) вр. ( )
вр. если J нечетно; вр. если J четно;
45.
Вращательная и ядерная суммыгомоядерной двухатомной молекулы А2
пост. кол. эл. яд. вр.
Для молекулы из ядер с нечетной массой :
пост. кол. эл. яд. вр.
яд. ( ) вр. ( ); яд. ( ) вр. ( )
вр. если J нечетно; вр. если J четно;
46.
Вращательная и ядерная суммыгомоядерной двухатомной молекулы H2
QядQвр g яд as Qвр s , чт. J g яд s Qвр as , нчт. J
1
T
Qвр Qвр чт Qвр нчт
2
2 вр
gяд (s)= 3
gяд (as) = 1
(-)Ψяд
(+) Ψяд
Орто- Н2
Вр. уровни
Пара- Н2
47.
Пара- и орто-водород при низких температурах.Qвр. (2 J 1) e
h2
8 2 IkT
J ( J 1)
;
J 0
вр.
h
8 Ik
Пара- Н2 Qяд( as), Qвр(s, J=0,2….)
Qврч 1 5e
6 h2
8 2 I kT
.....( J 0, 2,....)
Орто- Н2 (Qяд(s), Qвр(as, J=1,3….)
Qврнч 3e
2 h2
8 I kT
2
7e
12 h 2
8 2 I kT
2
.....( J 1,3,......)
2
48.
Вращательная теплоемкость Н2cV
Пара – Н2 (ас)
Q( s,чет. ) 1 5e
6
вр
T
...
R
300 К
H2
Орто – Н2 (с)
Q(аs,неч. ) 3e
2
вр
T
7e
12
вр
T
....
T
49.
Расчет термодинамических функцийZ;
Qe
ln Z N ln
;
N
QN
Z
N!
ln Z
ln Q
N
;
T
T
V
V
F E0 kT ln Z RT ln
2 ln Z
2 ln Q
N
2
2
T
V
T V
Qe
N
Qe
F
ln Z
ln Q
S
k
ln
Z
kT
R
ln
RT
N
T V
T V
T V
ln Z
2 ln Q
U E0 F E0 TS kT ln Z kT ln Z kT 2
RT
T V
T V
G E0 F E0 pV kT ln Z RT RT ln
Qe
Q
RT ln e RT ln
N
N
50.
Расчет термодинамических функцийE0 kT ln Z RT RT ln
Q
N
ln Z
ln Z
2 ln Q
H E0 U E0 PV kT 2
kT
V
RT
RT
T
V
T
V
T
V
2
2
U
ln Z
ln Q
2 ln Z
2 ln Q
сv
2RT
2kT
kT
RT
2
2
T
T
T
T V
T V
V
V
V
2
2
H
ln Z
ln Q
2 ln Z
2 ln Q
ср
2 RT
R
2kT
kT
RT
2
2
T p
T p
T p
T p
T p









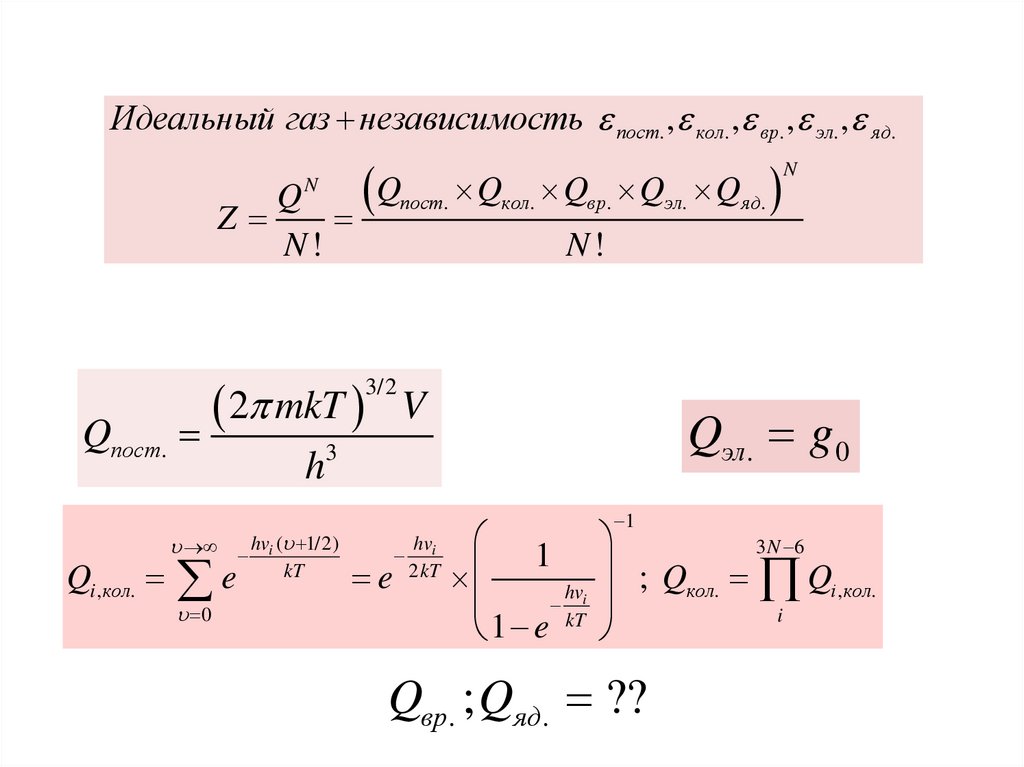































 Физика
Физика








