Похожие презентации:
Интегрирование методом замены переменной
1.
Интегрирование методомзамены переменной
2.
Цель урока:Способствовать
формированию
представлений об интегрировании
методом замены переменной.
Способствовать
формированию
умения применять метод замены
переменной
при
нахождении
интегралов.
3.
Нужно выполнить преобразование:f ( x) dx
1. Заменяем переменную:
2. Дифференцируем: dx
F (u )du
x (u )
(u ) du
3. Подставляем вместо x и dx значения u и du:
f ( x ) dx
f [ (u )] (u ) du
4. С помощью подстановки: u
Приводим интеграл к переменной x.
( x)
F (u )du
4.
1) (3 x 2) 5 dx3x 2 u
3dx du
1
dx du
3
6
1
1
u
1 6
5
5
(3x 2) dx 3 u du 3 6 C 18 u C
1 6
1
5
6
(
3
x
2
)
dx
u
C
(
3
x
2
)
C
18
18
1
6
6
d [ (3 x 2) C ]
(3 x 2) 5 3 xdx (3 x 2) 5 dx
8
18
5.
2) ( 2 x 3 1) 4 x 2 dx2 x 3 1 u
6 x 2 dx du
1
2
x dx du
6
5
1
1
u
1
3
4 2
4
3
5
(
2
x
1
)
x
dx
u
du
C
(
2
x
1
)
C
6
6 5
30
6.
xdx3) 2
( x 1)3
x 2 1 u
2xdx du
1
xdx du
2
2
xdx
1
1
u
2
3
3
(
x
1
)
xdx
u
du
C
( x 2 1)3
2
2 2
1
1
C
C
2
2
2
4u
4( x 1)
7.
x 2 dx4) 3
5 x 1
5 x 3 1 u
15 x 2 dx du
1
2
x dx
du
15
x 2 dx
1 du
1
1
3
ln
u
C
ln
5
x
1 C
5x3 1 15 u 15
15
8.
5) tgkxdxsin kx
tgkxdx cos kx dx
cos kx u
k sin kxdx du
1
sin kx du
k
1 du
1
1
tgkxdx k u k ln u C k ln cos kx C
9.
du6)
sin u
u
u
sin u 2 sin cos
2
2
du
du
sin u
u
u
2 sin cos
2
2
Разделим и умножим знаменатель на cos(u/2):
du
1
du
sin u 2 u 2 u
tg cos
2
2
10.
utg z
2
1
1
du dz
2
2 u
cos
2
du
u
cos
2
2dz
2
du
dz
u
sin u z ln z C ln tg 2 C
11.
du7)
cos u
du
du
cos u
sin( u )
2
u z
2
du dz
u
du
dz
z
u
2
ln
tg
C
ln
tg
C
ln
tg
(
) C
cos u sin z
2
2
4 2





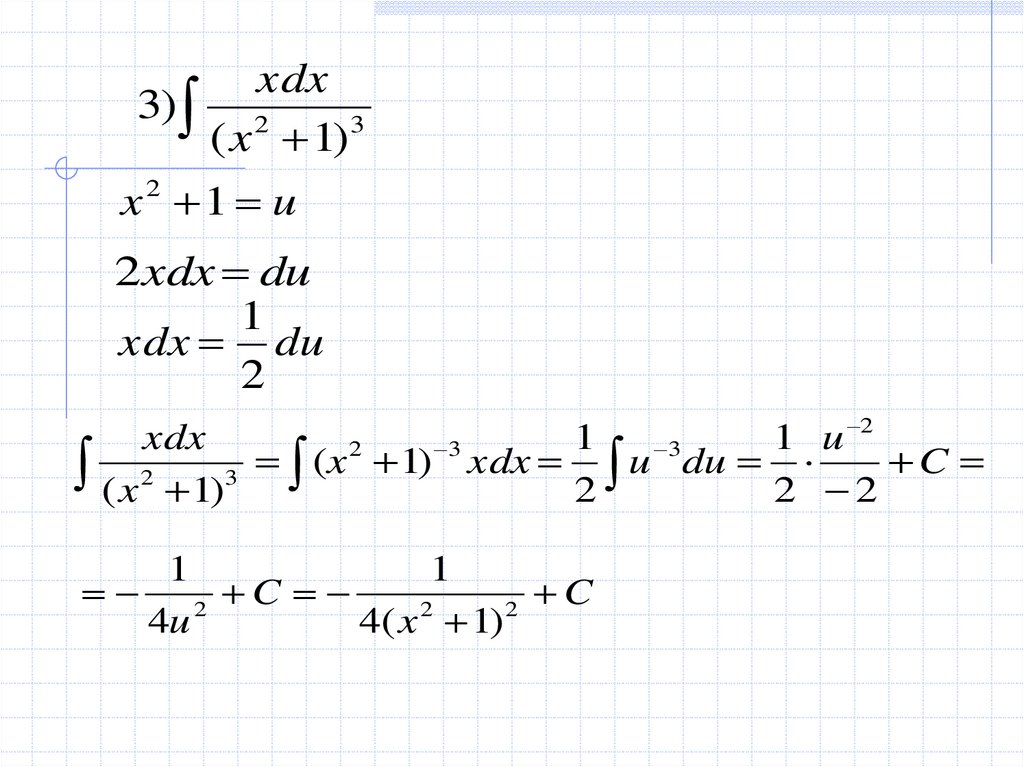
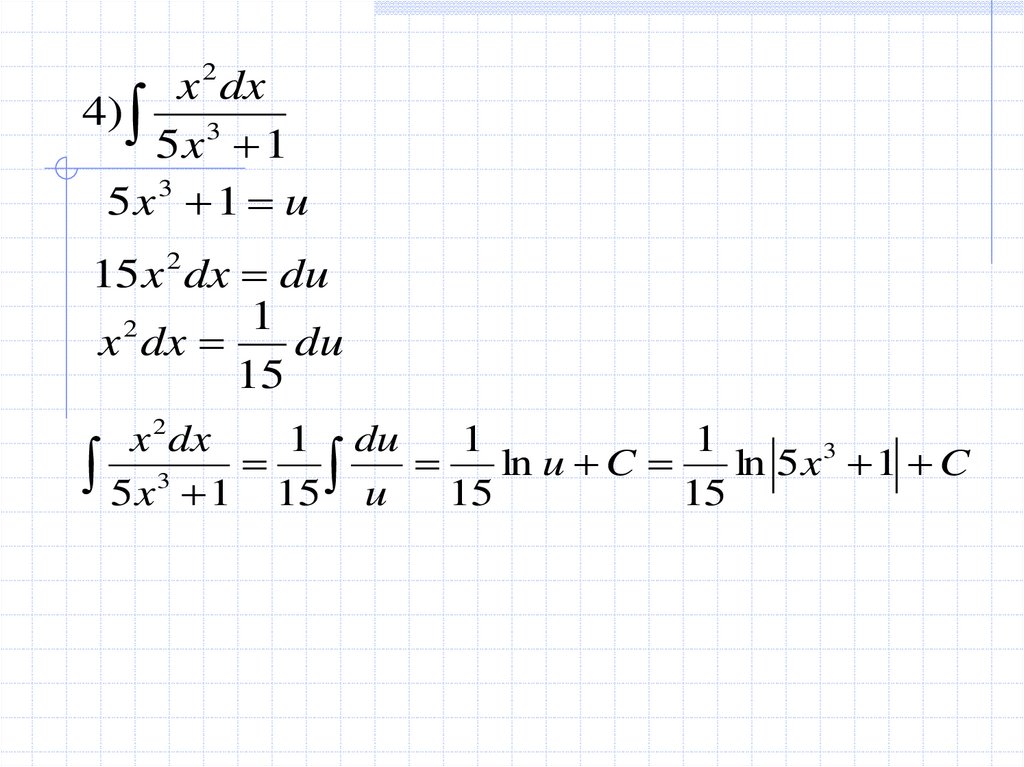
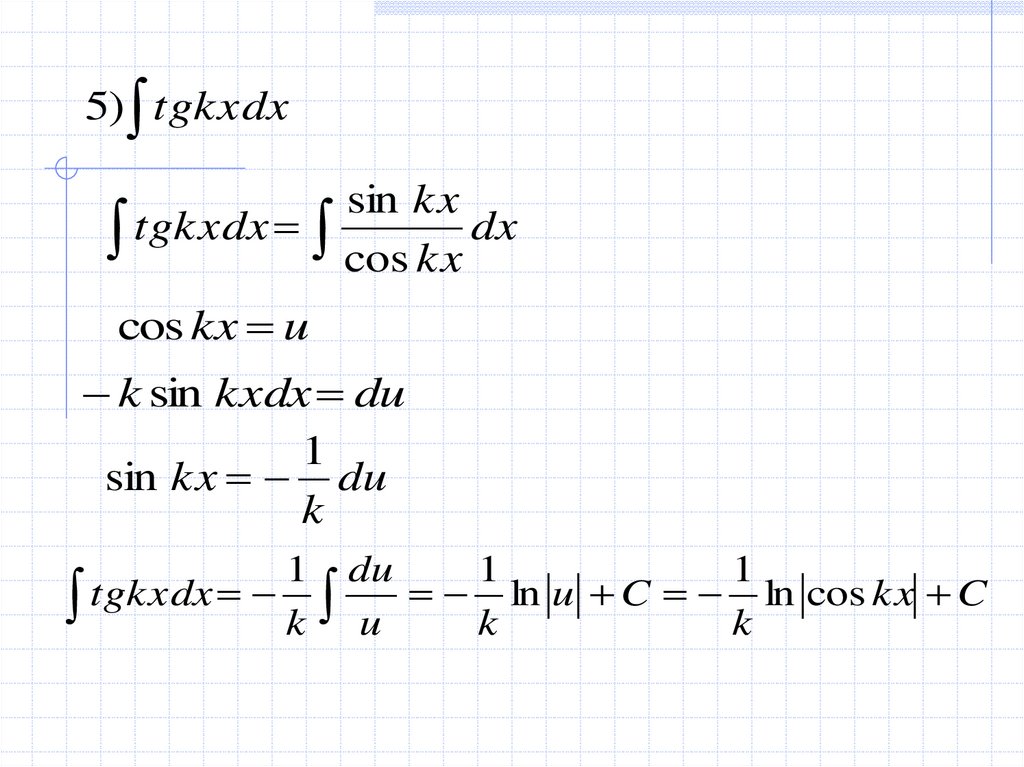

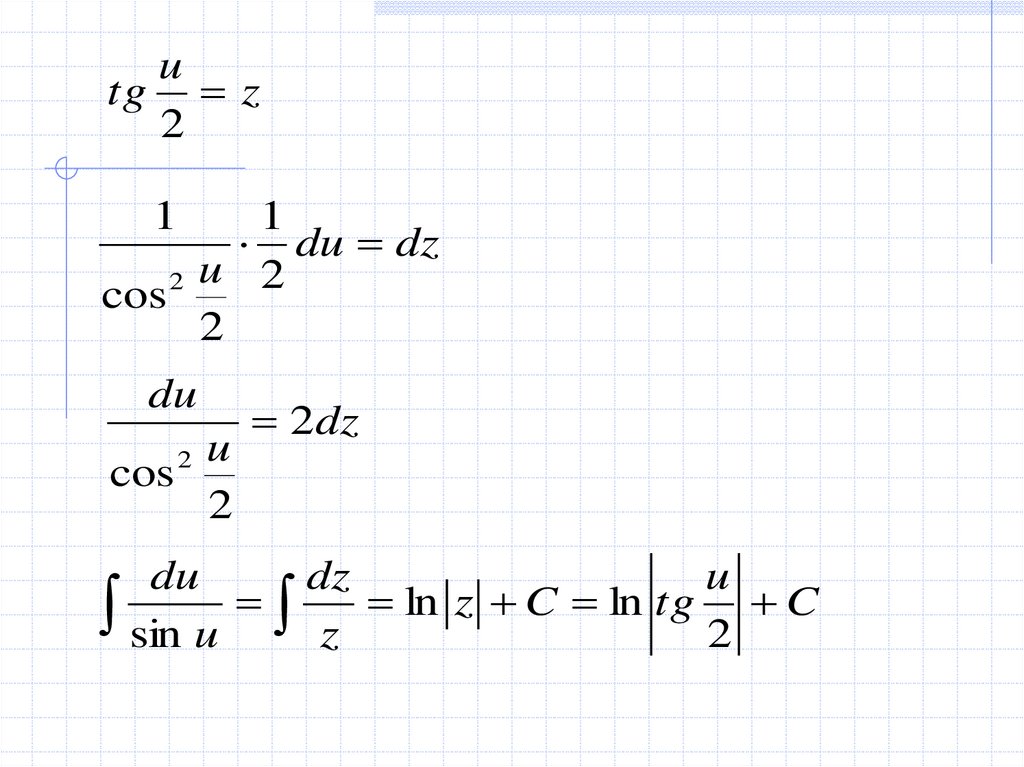
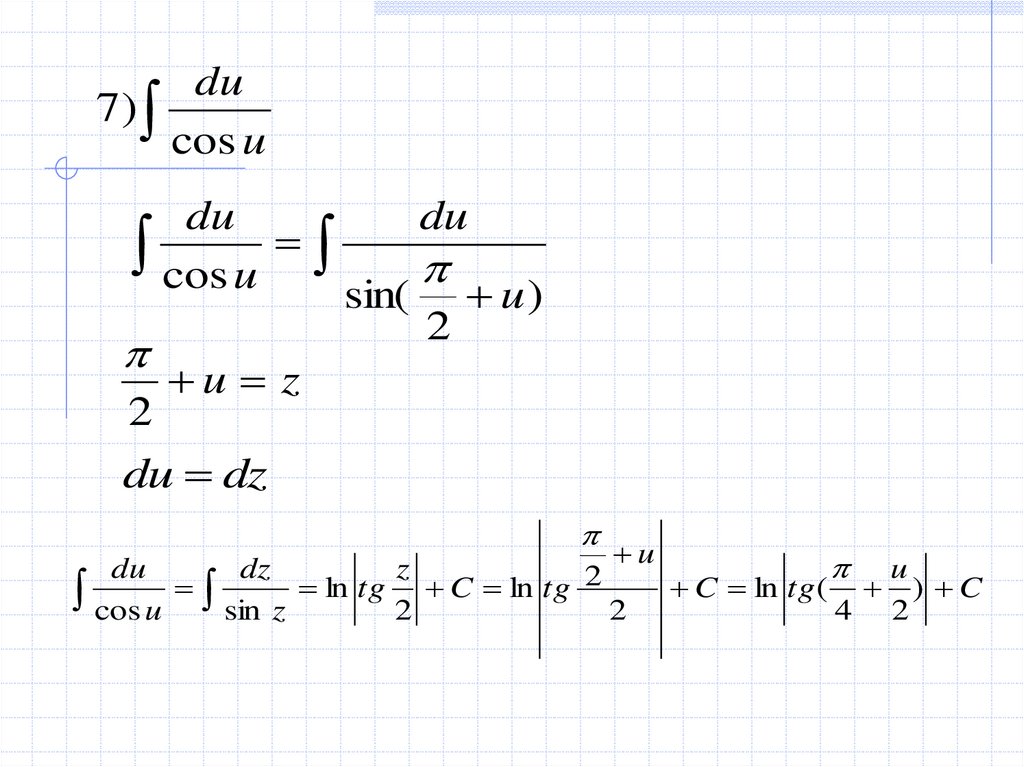
 Математика
Математика








