Похожие презентации:
Линейные уравнения с постоянными коэффициентами
1.
Линейные уравнения с постояннымикоэффициентами.
ДУ
( n 1)
an 1 ( x ) y
... a1 ( x ) y ' a0 ( x ) y f ( x ),
где a0 ( x ), a1 ( x ),..., an 1 ( x ), f ( x ) — заданные
y
(n)
функции, называется линейным.
Если
f ( x ) 0,
то уравнение называется линейным
однородным.
Если
f ( x ) 0,
то уравнение называется линейным
неоднородным.
2.
Рассмотрим решение линейных ДУ 2-гопорядка с постоянными коэффициентами ,т.е.
где p , q R .
y '' py ' qy f ( x ),
Решение ЛОДУ
Теорема 1 (свойство решений однородного
уравнения).
Пусть y1 ( x ), y2 ( x ) — частные решения ЛОДУ
y '' py ' qy 0.
Тогда линейная комбинация
y ( x ) C1 y1 ( x ) C 2 y2 ( x )
также частное решение этого ДУ.
3.
Доказательство.Так как
y ( x ), y ( x )
1
2
— решения ДУ
y '' py ' qy 0,
то
y1 py1 qy1 0,
Подставим
в уравнение.
При этом
y2 py2 qy2 0.
y C1 y1 C2 y2
y ' C1 y1 C 2 y2 ,
y '' C1 y1 C2 y2 .
4.
ПолучимC1 y1 C2 y2 p (C1 y1 C 2 y2 ) q (C1 y1 C 2 y2 )
(C1 y1 pC1 y qC1 y1 ) (C 2 y2 pC 2 y2 qC 2 y2 )
C1 ( y1 py qy1 ) C 2 ( y2 py2 qy2 ) 0.
Значит,
y C1 y1 C2 y2
— решение данного ДУ.
5.
Функции y1 ( x ) и y2 ( x ) называются линейнозависимыми, если
y1 ( x )
, const.
y2 ( x )
В противном случае функции называются
линейно независимыми.
Линейно независимые решения однородного
уравнения образуют фундаментальную
систему решений этого уравнения.
6.
Теорема 2 (о структуре общего решениялинейного однородного уравнения).
Если y1 ( x ) и y2 ( x ) — два линейно
независимых частных решения уравнения
y '' py ' qy 0,
то их линейная комбинация
y ( x ) C1 y1 ( x ) C 2 y2 ( x )
определяет общее решение этого уравнения.
7.
Метод Эйлера решения ЛОДУ спостоянными коэффициентами
Рассмотрим ДУ
y '' py ' qy 0.
Решение ищем в виде
x
y e , R.
Тогда
x
2 x
y ' e , y '' e .
Подставим в уравнение
2 x
x
x
e p e qe 0,
x
2
e ( p q ) 0.
(1)
8.
xe 0,
Так как
то
p q 0
2
(2)
— характеристическое уравнение данного ДУ.
Возможны случаи:
1) D 0.
Уравнение (2) имеет два разных
действительных корня 1 , 2 .
Решениями уравнения (1) являются функции
1 x
2 x
y1 e , y2 e .
9.
Так както функции
y1
( 1 2 ) x
e
const,
y2
1 x
y1 e , y2 e
2 x
линейно независимы.
По теореме 2 общее решение уравнение (1)
имеет вид
y C1e
1 x
2 x
C2e .
10.
2) D 0.Уравнение (2) имеет два одинаковых
действительных корня 1 2 .
Решением уравнения (1) является функция
x
y1 e .
Можно показать, что решением уравнения (1)
x
также является функция y 2 xe .
y1
Так как
y2
x const,
эти функции линейно независимы и
x
y C1e C 2 xe
— общее решение ДУ (1).
x
11.
3) D 0.Уравнение (2) имеет два комплексно
сопряженных корня 1,2 i .
Решениями уравнения (1) являются функции
( i ) x
x i x
x
y1 e
e e e (cos x i sin x ),
( i ) x
x i x
x
y2 e
e e
e (cos x i sin x ).
По теореме 1 решениями уравнения (1) также
являются функции
y1 y2
x
y1
e cos x,
2
y1 y2
x
y2
e sin x.
2i
12.
Так какy1
const,
y2
то функции y1 , y2 линейно независимы и
x
y e (C1 cos x C 2 sin x )
— общее решение ДУ (1).
13.
Пример. Решить уравнениеy '' 5 y ' 6 y 0.
Решение. Характеристическое уравнение
5 6 0,
D 49 0,
1 1, 2 6.
2
Общее решение имеет вид
x
y C1e C 2 e .
6x
14.
Пример. Решить уравнениеy '' 4 y ' 4 y 0.
Решение. Характеристическое уравнение
4 4 0,
D 0,
1,2 2.
2
Общее решение имеет вид
y C1e C 2 xe .
2x
2x
15.
Пример. Решить уравнениеy '' 2 y ' 5 y 0.
Решение. Характеристическое уравнение
2 5 0,
D 16 0,
1,2 1 2i.
2
Общее решение имеет вид
x
y e (C1 cos 2 x C 2 sin 2 x ).


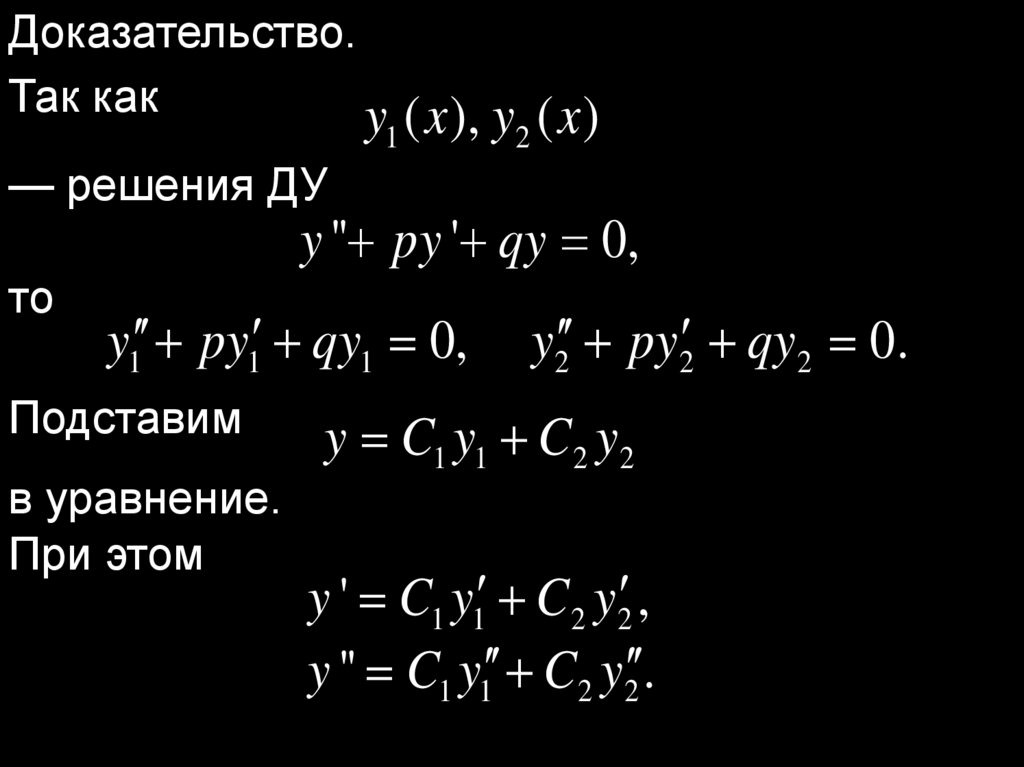












 Математика
Математика








