Полоса, нагруженная нормальным давлением на участках границ

1. Полоса, нагруженная нормальным давлением на участках границ

Московский ордена Ленина, ордена Октябрьской Революции и ордена Трудового Красного Знамени
государственный технический университет им. Н. Э. Баумана
Полоса, нагруженная
нормальным давлением
на участках границ
Выполнил студент группы РК5-83Б Шишлачёв А.О.
Руководитель: проф. Разумовский И. А.
Москва, 2019

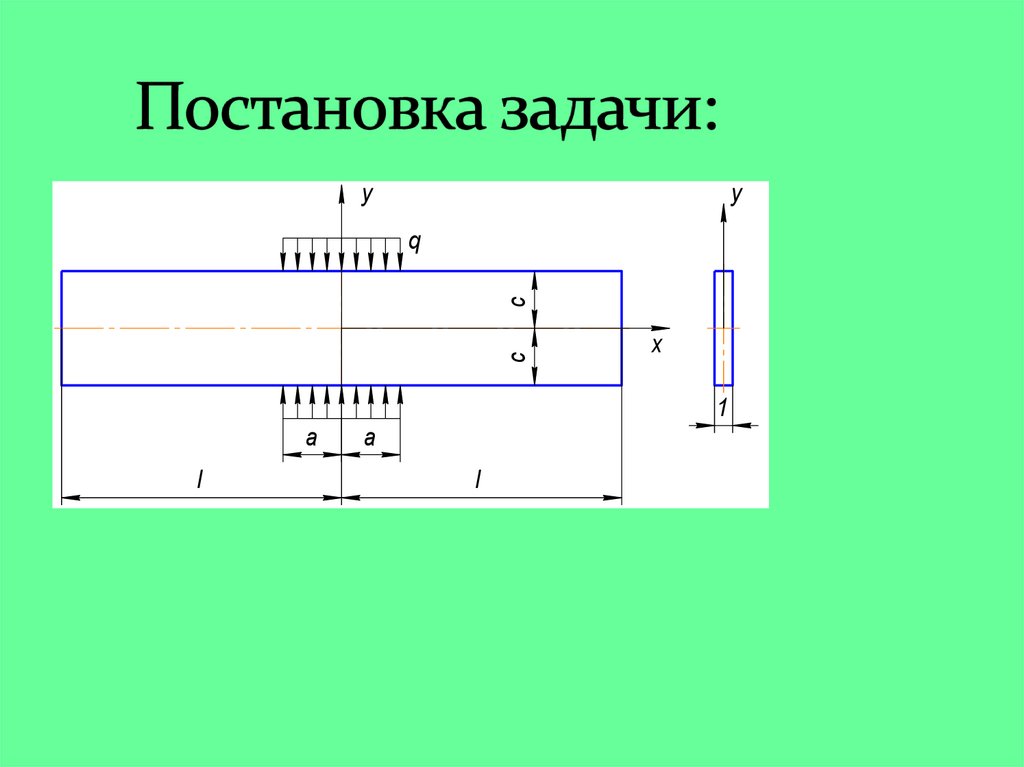
2.

y
y
c
c
q
x
1
a
l
a
l

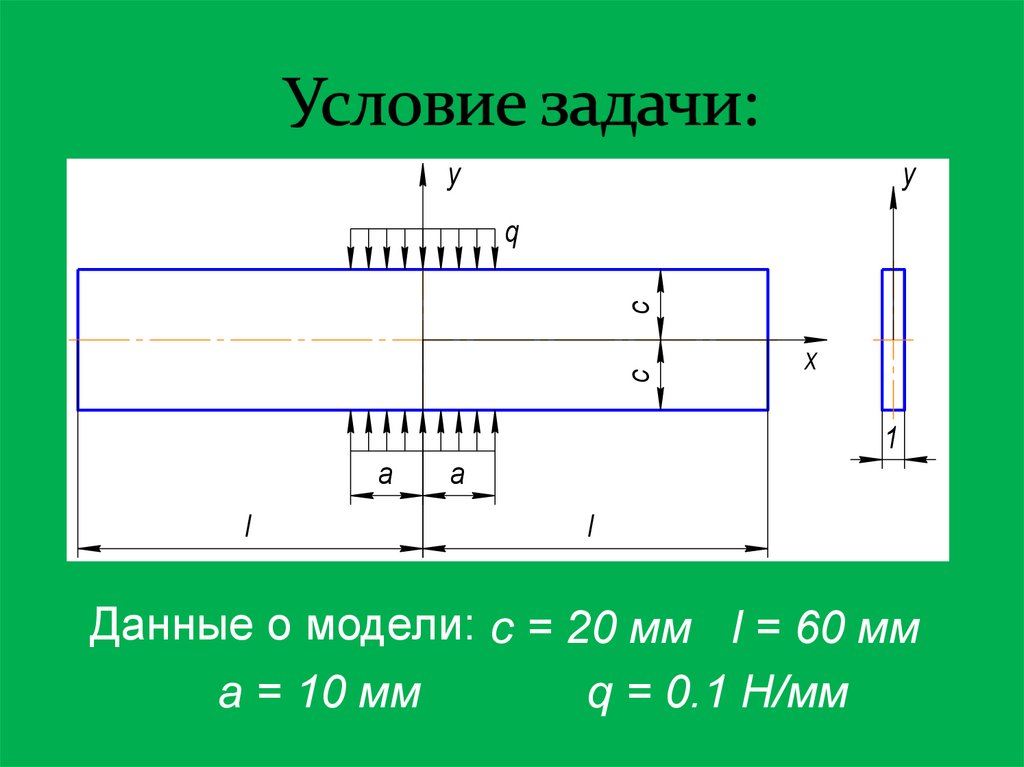
3. Условие задачи:

y
y
c
c
q
x
1
a
l
a
l
Данные о модели: c = 20 мм l = 60 мм
a = 10 мм
q = 0.1 Н/мм

4. Решение

Нагрузка:
- на верхней кромке
t1 (a0 a n cos( x))
n 1
- на нижней кромке
t2 b0 bn cos( x)
n 1
1
q a
t2 ( x) dx
где a0 b0
2 l l
l
l
1
2 q
n
an bn t2 ( x) cos( x)dx
sin( a),
l l
l
l
l

5. Напряжения под действием симметричной нагрузки

x
n 1
[C1n 2ch( y) C2 n 2 sh( y) C3n (2sh( y) y ch( y))
C4 n (2ch( y) y sh( y))]cos( x),
y ' 2 [C1n ch( y ) C2 n sh( y ) C3n y ch( y ) C4 n y sh( y )]cos( x)
n 1
[C1n sh( y) C2 n ch( y) C3n (ch( y) y sh( y))
xy
n 1 C4 n ( sh( y ) y ch( y ))]sin( x).

6. Граничные условия на продольных кромках

t1 ( y c) xy ( y c) 0
t2 ( y c) y '( y c) an cos( x)
n 1
t2 ( y c) y '( y c) bn cos( x).
n 1

7. Нахождение констант

4q
sh( c) c ch( c)
C1n 3 sin( a)
;
l
sh(2 c) 2 c
C2 n 0; C3n 0;
4q
sh( c)
C4 n 3 sin( a)
.
l
sh(2 c) 2 c

8. Формулы для напряжений

a
x 4q kn [ c ch( c) ch( y ) sh( c) (ch( y ) y sh( y ))]cos( x);
l n 1
a
l
a
xy 4q kn ( c ch( c) sh( y ) sh( c) y ch( y )) sin( x)
l n 1
y q {1 4 kn [ c ch( c) ch( y ) sh( c)( y sh( y ) ch( y ))]cos( x)};
kn
sin( a)
a( sh(2 c) 2 c)

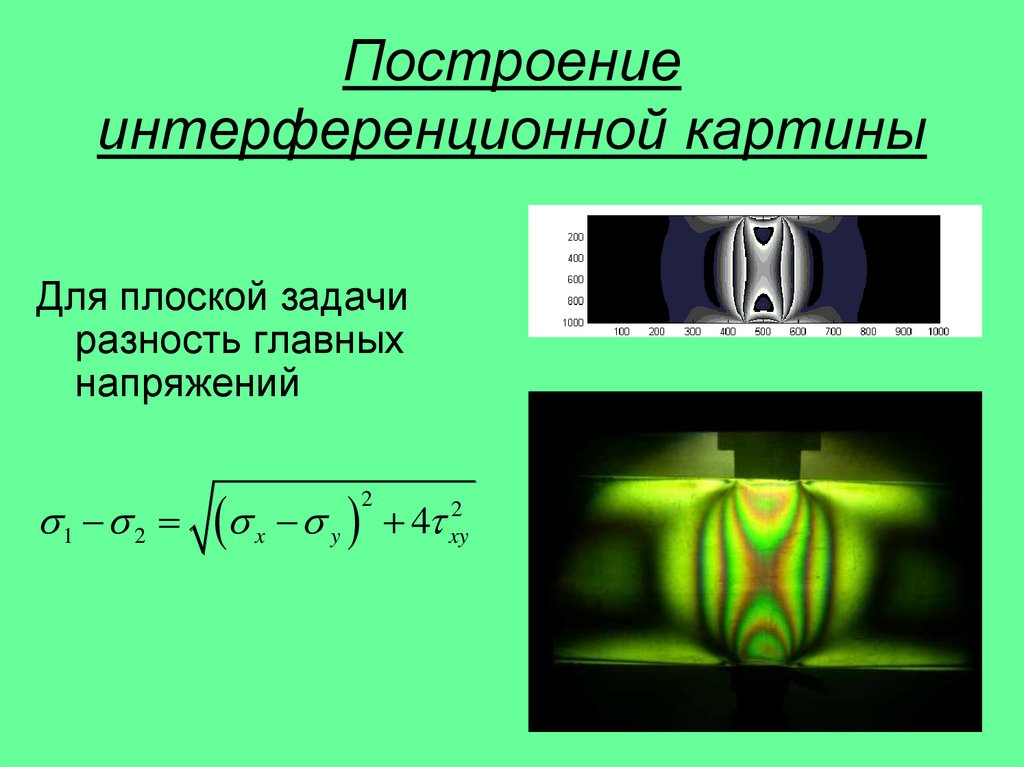
9. Построение интерференционной картины

Для плоской задачи
разность главных
напряжений
1 2
2
4
x y xy
2

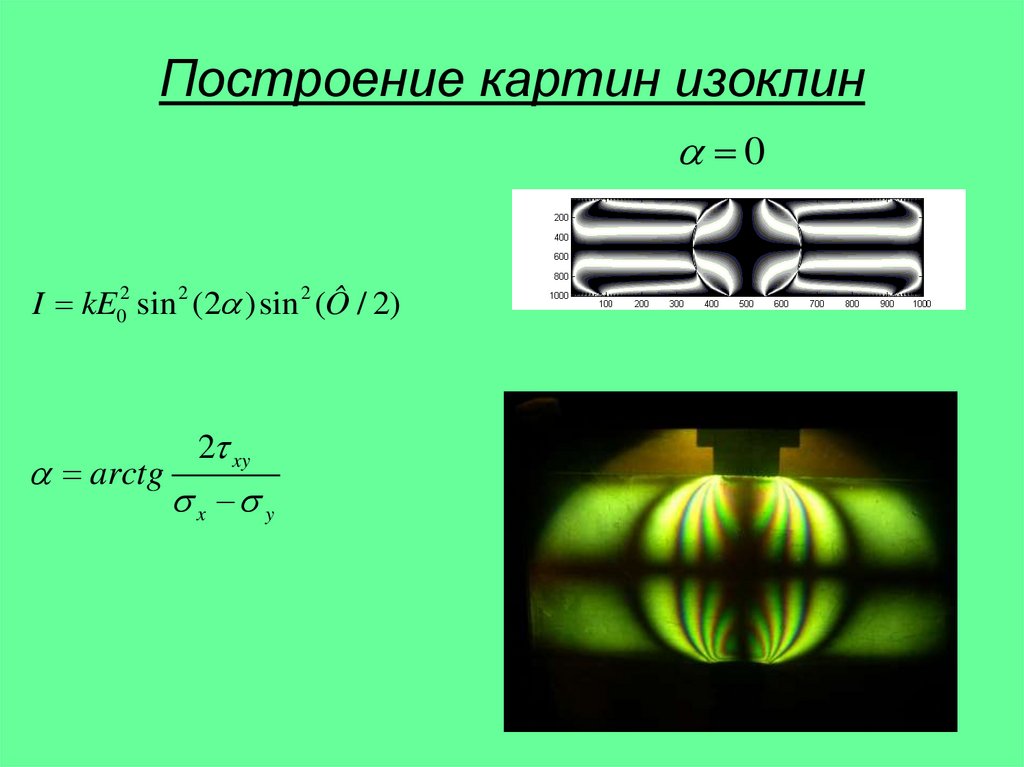
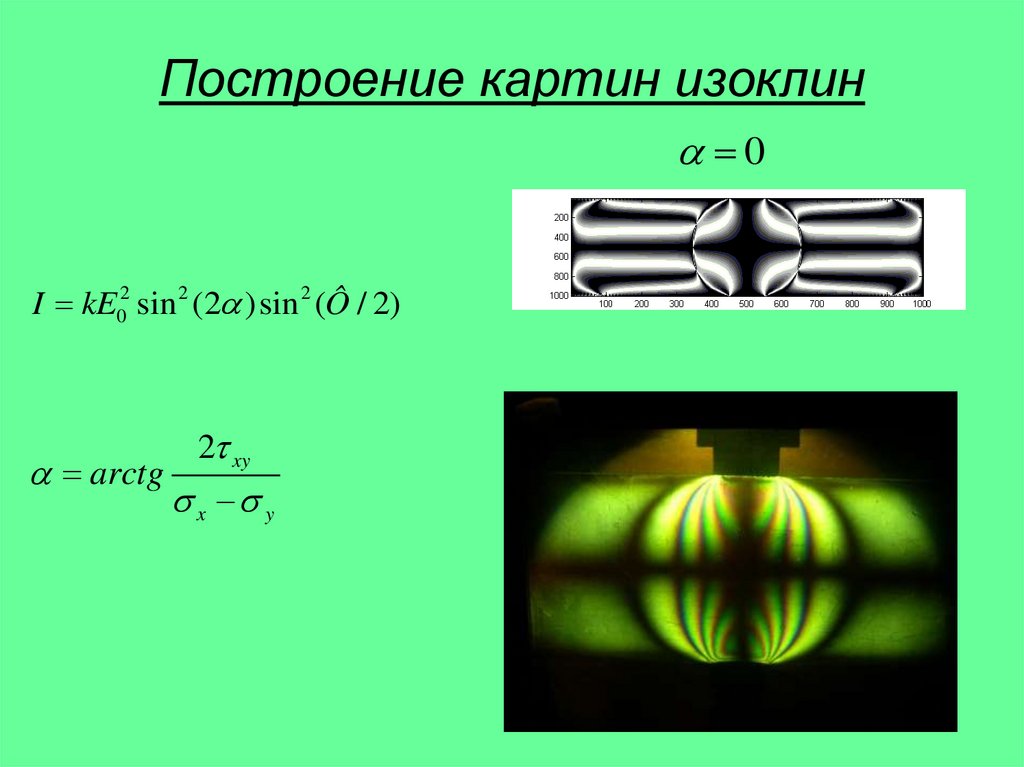
10. Построение картин изоклин

0
I kE02 sin 2 (2 ) sin 2 (Ô / 2)
arctg
2 xy
x y

11. Построение картин изоклин

0
I kE02 sin 2 (2 ) sin 2 (Ô / 2)
arctg
2 xy
x y

12.

15
30
45

13.

ВЫВОДЫ
Мы показали на простой модели, что аналитическое
решение имеет очень большое сходство с практическим,
поэтому метод фотоупругости можно применять для
сложных моделей, где аналитическое решение требует
очень больших подсчетов
или не возможно сделать
вообще.
При увеличении членов ряда аналитическое решение
становиться более точным, но увеличивается время
выполнения счета, поэтому нельзя брать меньше 15 членов,
так как будет большое расхождение с методом фотоупругости,
но не стоит брать больше 25, так как изменение картины
почти незаметно.