Нормальные поля

1. 3.1 Нормальные поля

3. Метод сопротивления
3.1 Нормальные поля

2. Поле точечного источника

Уравнение Лапласа в сферической системе координат
1 2 U
1
U
1 2U
0
r
sin
r 2 r r r 2 sin
r 2 sin 2
С учетом симметрии:
1 2 U
r
0
2
r r r
I
r0
Iρ0 1
U
2 r

3. Понятие кажущегося сопротивления

Нормальное поле – поле в однородной среде:
Ir 0 1
1
1
1
U 0
2 AM AN BM BN
В неоднородной среде:
rk
U
или
U 0 r 0
где L – нормальное поле при I=1, r0=1
1 1
1
1
1
L
2 AM AN BM BN
rk
U
U
K
L I
I

4.

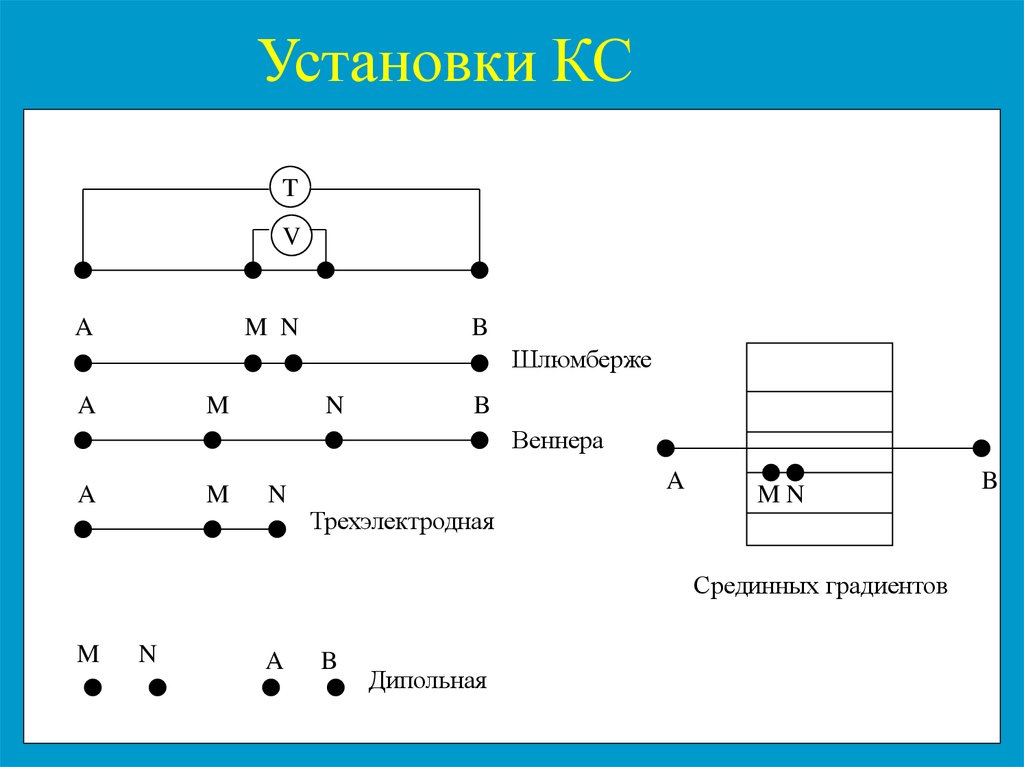
Установки КС
T
V
A
M N
B
Шлюмберже
A
M
N
B
Веннера
A
M
N
A
Трехэлектродная
MN
Срединных градиентов
M
N
A
B
Дипольная
B

5. Поле дипольного источника

A
B
Q
r1
M
r
r2
Ir
U d (M )
2
1 1 Ir r2 r1
r1 r2 2 r1r2
r2 r1 AB cos Q
r1r2 r 2
Ir AB
pr
U d (M )
cos Q
cos Q
2
2
2 r
2 r

6.

Найдем компоненты поля диполя в полярной системе координат
U d (M )
pr
cos Q
2
2 r
Er
U pr
pr
3 cos Q 4 x
r r
r
EQ
1 U
pr
pr
sin
Q
y
3
4
r Q 2 r
2 r
y
L
M
Вдоль оси x:
N
Q
p
Q 0 : Er
pr
; EQ 0
3
r
MN
x
pr
Вдоль оси y: Q ; Er 0; EQ
2
2 r 3
Дипольная осевая и дипольная экваториальная установки

7. Анизотропия удельного сопротивления

y
Анизотропия удельного
сопротивления
x
rl
z
r2 r1
rn

8. Выясним соотношение n и l

n
Выясним соотношение n и l
l ( 1d1 2 d 2 )( r1d1 r 2 d 2 )
2
n
(d1 d 2 )
d12 d1d 2 1 r 2 d1d 2 2 r1 d 22
2
(d1 d 2 )
l
1,
d1
l
n
r 2 r1
d d d1d 2
r1 r 2
(d1 d 2 ) 2
2
1
2,
d2
1d1 2 d 2
d1 d 2
d1 d 2
r1d1 r 2 d 2
r2
r1
1 r1
x r2
x
2
2
1
x 2
x
x2 2x 1 0
x 1 l n

9.

Плотность тока:
1 U
jx
rn
r n x
1 U
jy
r
r y
Ex
Ey
1 U
jz
rl
rl z
Ez
В среде нет источников тока:
1 2U 1 2U 2U
divj 2 2 2 0
r n x
r z
y
Введем новые координаты: x1 x r n
U U x1 U
x x1 x x1
rn
y1 y r
z1 z rl
2U 2U
2U x1
2U
rn 2
rn rn 2
2
x
x1 x
x 1 x
x 1
2U 2U 2U
divj 2 2 2 0
y1
z1
x1

10.

Решение:
U
Ir r n
4 r n x 2 r l ( y 2 z 2 )
Введем коэффициент анизотропии:
rn
1
rl
2
2
2
r
x
r
(
y
z
) const
Линии равного потенциала: n
l
x2
rl
y2
rn
z2
rn
const
Концентрические сжатые эллипсоиды вращения, малая ось
направлена вдоль оси X

11.

U
Для анизотропного полупространства:
и на дневной поверхности:
U
Ir r n
Ir r n
2 r n x 2 r l ( y 2 z 2 )
2 r n x 2 r l y 2
у
Введем полярные координаты:
r
x r cos b ; y r sin b
b
x
U
Ir r n
2 r n r cos b r l r sin b
2
2
2
Ir r n
2 r r n cos 2 b r l sin 2 b
U
Ir эфф
2 r
2

12.

у
r эфф ( b )
r эфф (0)
r rn
r n cos 2 b r l sin 2 b
r r n
r
rn
r r n
r эфф ( / 2)
r r n
rl
r
b
x
Среднее геометрическое сопротивление
r эфф ( / 2)
rl r n
rn
r эфф (0)
rl
rl
Эффективное (кажущееся) сопротивление в направлении
слоистости – больше, чем в направлении вкрест слоистостиПарадокс анизотропии!

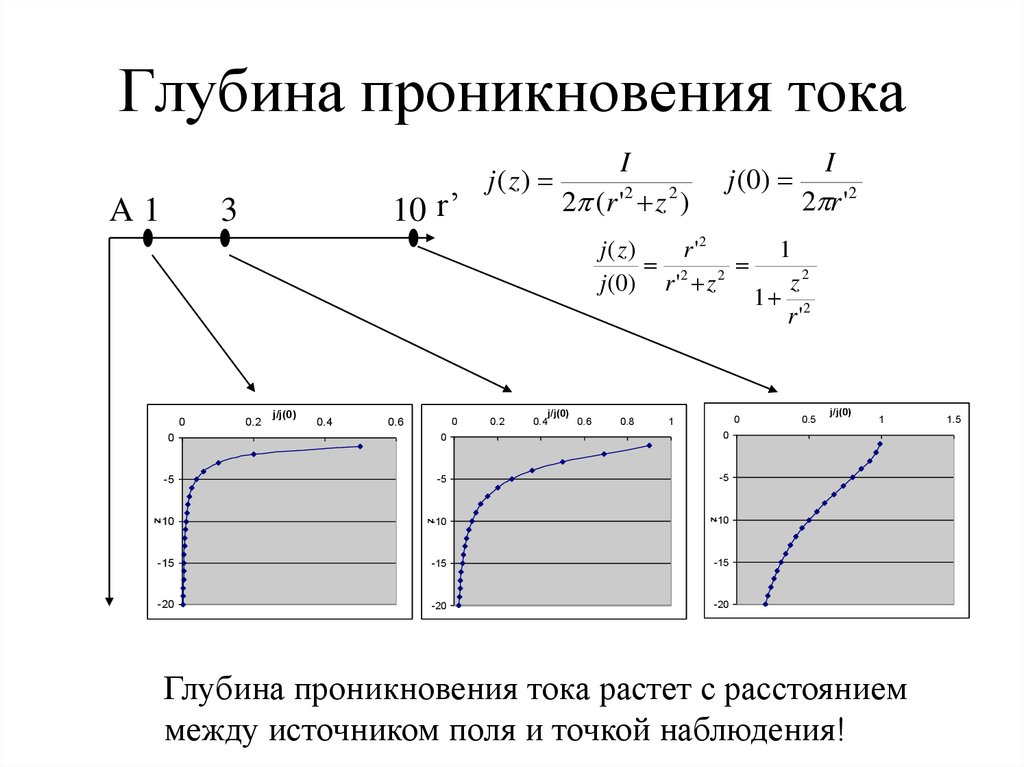
13. Глубина проникновения тока

A1
10 r’
3
j( z)
I
2 (r '2 z 2 )
j ( 0)
j( z)
r '2
2 2
j (0) r ' z
0
0.2
j/j(0)
0.4
0
0.6
0.2
j/j(0)
0.4
0.6
0.8
0
1
-5
-5
-5
-10
-10
-10
1
z2
1 2
r'
0.5
j/j(0)
1
z
0
z
0
z
0
I
2 r '2
-15
-15
-15
-20
-20
-20
Глубина проникновения тока растет с расстоянием
между источником поля и точкой наблюдения!
1.5