Похожие презентации:
Электростатическая теорема гаусса (ЭТГ). Лекция 2
1. ЛЕКЦИЯ 2 ЭЛЕКТРОСТАТИЧЕСКАЯ ТЕОРЕМА ГАУССА (ЭТГ)
1.2.
3.
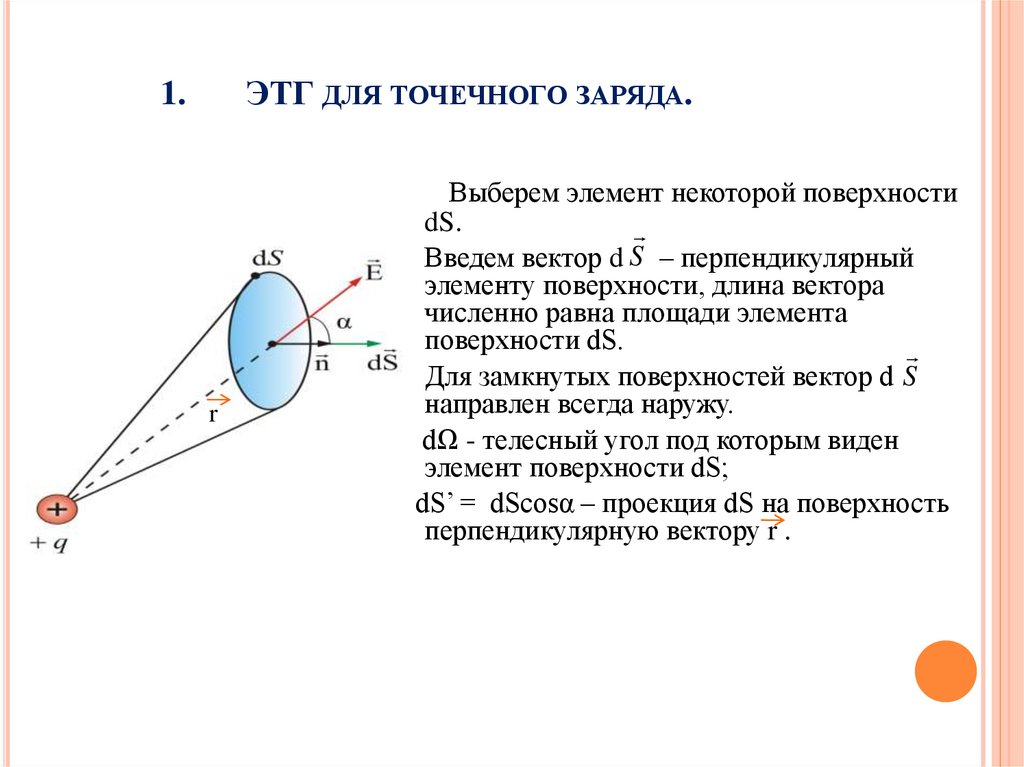
ЭТГ для точечного заряда.
ЭТГ для системы зарядов и для
непрерывно распределённого заряда.
Закон Кулона в дифференциальной
форме. Электрические заряды как
источник электрического поля.
2.
Остроградский Михаил Васильевич(1801 – 1862)
отечественный математик и механик.
Учился в Харьковском ун-те (1816 – 1820),
совершенствовал знания в Париже (1822
– 1827).
Основные работы в области
математического анализа,
математической физики, теоретической
механики.
Решил ряд важных задач гидродинамики,
теории теплоты, упругости, баллистики,
электростатики, в частности задачу
распространения волн на поверхности
жидкости (1826 г.).
Получил дифференциальное уравнение
распространения тепла в твердых телах и
жидкостях.
Известен теоремой Остроградского-Гаусса
в электростатике (1828 г.).
2
3.
Гаусс Карл Фридрих (1777 – 1855) немецкийматематик, астроном и физик.
Исследования посвящены многим разделам физики.
В 1832 г. создал абсолютную систему мер (СГС),
введя три основных единицы: единицу времени – 1 с,
единицу длины – 1 мм, единицу массы – 1 мг.
В 1833 г. совместно с В. Вебером построил первый в
Германии электромагнитный телеграф.
Еще в 1845 г. пришел к мысли о конечной скорости
распространения электромагнитных взаимодействий.
Изучал земной магнетизм, изобрел в 1837 г.
униполярный магнитометр, в 1838 г. – бифилярный.
В 1829 г.
Сформулировал принцип наименьшего
принуждения (принцип Гаусса).
Один из первых высказал в 1818 г. предположение о
возможности существования неевклидовой
геометрии.
3
4. ЭТГ для точечного заряда.
ЭТГ ДЛЯ ТОЧЕЧНОГО ЗАРЯДА.1.
r
Выберем элемент некоторой поверхности
dS.
Введем вектор d S – перпендикулярный
элементу поверхности, длина вектора
численно равна площади элемента
поверхности dS.
Для замкнутых поверхностей вектор d S
направлен всегда наружу.
dΩ - телесный угол под которым виден
элемент поверхности dS;
dS’ = dScosα – проекция dS на поверхность
перпендикулярную вектору r .
5.
Пусть q >0, тогда векторE r .Найдем поток вектора E через элемент поверхности dS:
EdS
(1)
S
1 q
d E dS
r dS
3
4 0 r
1 q
1
q
3 r dS cos
2 dS '
4 0 r
4 0 r
2
dS
'
r
d )
(dS’–можно считать элементом сферы, тогда
6.
1 q 21
2 r d
q d
4 0 r
4 0
EdS
S
4
q
4 0
q
d
0
0
-выполняется для поверхности S любой формы.
q
EdS
(2)
S
0
При этом заряд находиться внутри
ограниченной поверхности S.
7. Рассмотрим случай, когда заряд находится вне ограниченной поверхности.
РАССМОТРИМ СЛУЧАЙ, КОГДА ЗАРЯД НАХОДИТСЯВНЕ ОГРАНИЧЕННОЙ ПОВЕРХНОСТИ.
E2 E1
E2
, при этом вектор
1
dS1 1
EE
11
d 0
E2
2
q1 0
dS2
E2
2
расположен ближе к заряду.
1
2
cos 1 0
dS1' dS1 cos 1
2
2
cos 2 0
dS2' dS2 cos 2
8.
q4 0
0
q
0
d 4 d 0
0
(3)
0 0
(2.3)-ЭТГ для случая, когда заряд находится вне ограниченной поверхности.
Электростатическая теорема Гаусса для точечного
заряда:
q
EdS 0
S
0
, если q находится внутри
ограниченной области
(4)
, если q находится вне
ограниченной области
Результат 2.4 не зависит от формы поверхности S и определяется только
величиной заряда.
9. 2. ЭТГ для системы зарядов и для непрерывно распределённого заряда.
2. ЭТГ ДЛЯ СИСТЕМЫ ЗАРЯДОВ И ДЛЯНЕПРЕРЫВНО РАСПРЕДЕЛЁННОГО ЗАРЯДА.
Рассмотрим систему точечных зарядов и
поверхность S произвольной формы, часть
зарядов находится внутри объёма, а часть –
снаружи объёма.
q
q
q 11
5
q2
3
q
4
10.
EdS Ek dSS
S k 1
n
(применим принцип суперпозиции
Ek - поле, созданное зарядом qk )
n
=
Ek dS
k 1 S
Где
Q q1 q2 q5
n
qk
k 1
0
n
E Ek , где
k 1
Q
0
- суммарный электрический заряд внутри области.
Q
EdS
S
0
(5)
11. ЭТГ для непрерывно распределённого заряда
ЭТГ ДЛЯ НЕПРЕРЫВНО РАСПРЕДЕЛЁННОГОЗАРЯДА
Рассмотрим некоторую область объёмом V, в которой
заряженные частицы расположены настолько плотно, что можно
говорить о непрерывном распределении заряда.
Выделим некоторую малую область dV, имеющую суммарный
электрический заряд dq.
Тогда
dq
dV - объёмная плотность
заряда.
dq
dV
dq dV
(6)
12. ЭТГ для непрерывно распределённого заряда:
Q 11
EdS dq dV
0
0
0V
S
ЭТГ ДЛЯ НЕПРЕРЫВНО РАСПРЕДЕЛЁННОГО ЗАРЯДА:
1
EdS
S
0
dV
V
(7)
13. 3. Закон Кулона в дифференциальной форме.
3. ЗАКОН КУЛОНА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ.1
E
d
S
Применим к
S
0
dV
V
теорему Остроградского-Гаусса { AdS
S
E dS
S
divAdV , div-скаляр}
V
divEdV
V
1
V divEdV 0 V dV
Это соотношение справедливо для любого объёма V, когда два интеграла
равны, то равны подынтегральные функции:
14.
divE0
(8)
(2.8) – закон Кулона в дифференциальной форме.
Формулировка "закон записан в дифференциальной форме"
означает:
• все используемые величины относятся к любой, но к одной и той же
точке пространства;
• при записи закона использованы производные физических величин
по пространственным координатам.
Другими словами, закон, записанный в дифференциальной форме,
справедлив для любой физически малой области пространства. Поэтому
говорят, что такой закон имеет локальную формулировку.
15.
Дивергенция вектора в некоторой точке пространства, то есть вфизически малом объёме, характеризует расходимость линий вектора и наличие
источников линий вектора в этой точке пространства.
,
Физический смысл закона Кулона в дифференциальной форме:
силовые линии напряжённости электрического поля начинаются на
положительных («+») зарядах и заканчиваются на отрицательных («-»).
Электрические
заряды являются источниками электрического поля.
dS
α
E
q>0
divE 0
EdS 0
EdS cos 0 , т.е. вектор E направлен наружу поверхности.
( cos 0
2
)














 Физика
Физика








