Дискретні випадкові величини. Поняття «випадкової величини»

1.

ДИСКРЕТНІ ВИПАДКОВІ ВЕЛИЧИНИ
Поняття «випадкової величини»
Визначення:
1) Випадковою величиною називається змінна величина, яка в залежності від результату випробування
випадково приймає одне значення з безлічі можливих значень.
2) Випадкова величина, яка приймає різні значення, які можна записати у вигляді кінцевої або
нескінченної послідовності, називається дискретною випадковою величиною.
3) Випадкова величина, яка може приймати всі значення з деякого числового проміжку, називається
безперервною випадковою величиною.
4) Під сумою (добутком) випадкових величин X і У розуміють випадкову величину Z = Х + У (Z = ХУ),
можливі значення якої складаються з сум (добутків) кожного можливого значення величини X і
кожного можливого значення величини У.
X: x1, x2
Y: y1,y2
Z=Х+У
Z: x1+y1, x1+y2, x2+y1, x2+y2.
Закон розподілу дискретної випадкової величини
X
x1
x2
x3
x n-1
xn
P
p1
p2
p3
p n-1
pn
p1 p2 pn 1

2.

ДИСКРЕТНІ ВИПАДКОВІ ВЕЛИЧИНИ
Математичне очікування дискретної випадкової величини
X
x1
x2
x3
x n-1
xn
P
p1
p2
p3
p n-1
pn
Визначення:
1) Математичним очікуванням М(Х) випадкової величини X називається сума добутків всіх можливих
значень величини X на відповідні ймовірності: M X x1 p1 x2 p2 xn pn
Теорема:
Математичне очікування дискретної випадкової величини X приблизно дорівнює
арифметичному всіх її значень (при досить великій кількості випробувань) xср M X
середньому
2

3.

Властивості математичного очікування дискретної випадкової величини
4) М(Х-У) = М(Х) - М(У)
5) М(Х У) = М(Х) М(У)
1 ) М ( С ) = С 1 = С
2) М(СХ) = СМ(X)
3) М(Х+У) = М(Х) + М(У)
Дисперсія дискретної випадкової величини
X
2
0
2
У
100
0
100
P
0,4
0,2
0,4
P
0,3
0,4
0,3
М ( Х ) = 2 0,4 + 0 0,2 + 2 0,4 = 0,0;
М(У) = 100 0,3 + 0 0,4+ 100 0,3 = 0,0.
Незважаючи на те що МО величин X і У однакові проте можливі значення величин X і У
«розкідані» або «розсіяні» близько своїх МО по різному: можливі значення величини X
розташовані набагато ближче до свого МО, ніж значення величини У.
3

4.

Дисперсія дискретної випадкової величини
X
x1
x2
x3
x n-1
xn
P
p1
p2
p3
p n-1
pn
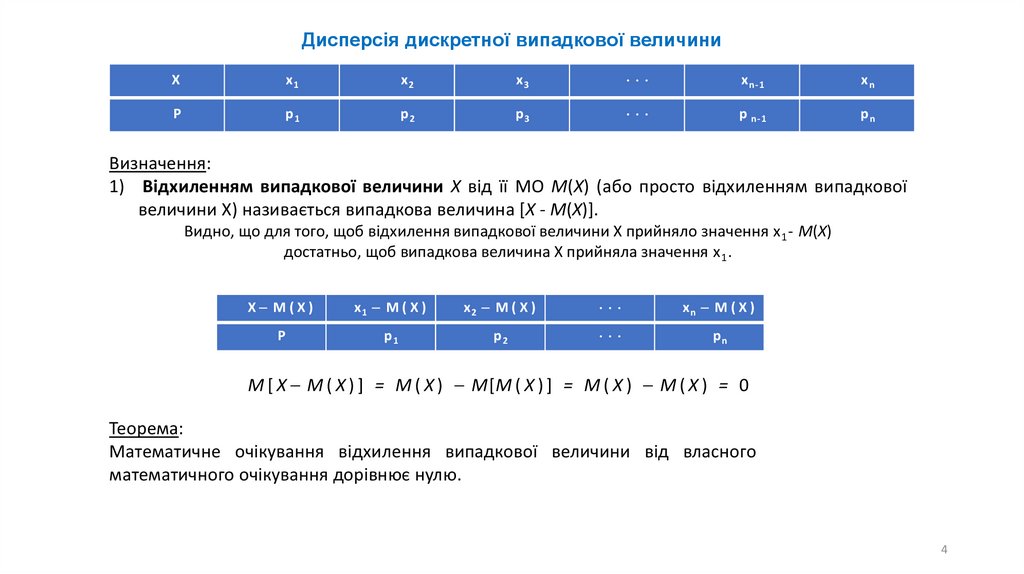
Визначення:
1) Відхиленням випадкової величини X від її МО М(Х) (або просто відхиленням випадкової
величини X) називається випадкова величина [X - М(Х)].
Видно, що для того, щоб відхилення випадкової величини X прийняло значення x 1 - М(Х)
достатньо, щоб випадкова величина X прийняла значення x 1 .
X М(Х)
x1 М ( Х )
x2 М ( Х )
xn М ( Х )
P
p1
p2
pn
М [ X М ( Х ) ] = М ( Х ) М[М ( X ) ] = М ( Х ) М ( X ) = 0
Теорема:
Математичне очікування відхилення випадкової величини від власного
математичного очікування дорівнює нулю.
4

5.

Дисперсія дискретної випадкової величини
[ X М ( Х ) ] 2
[ x 1 М ( Х ) ] 2
[ x 2 М ( Х ) ] 2
[ x n М ( Х ) ] 2
P
p1
p2
pn
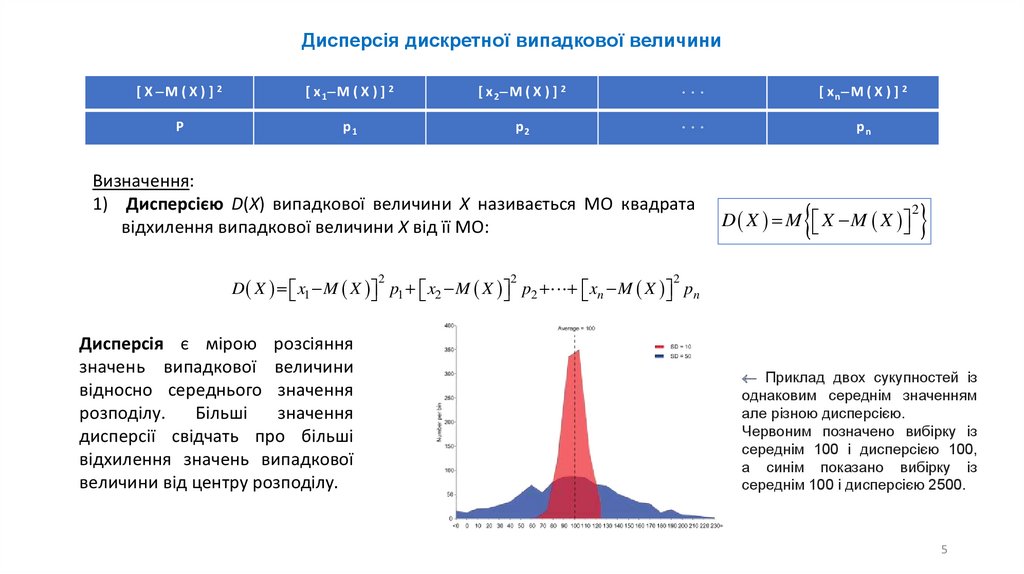
Визначення:
1) Дисперсією D(Х) випадкової величини X називається МО квадрата
відхилення випадкової величини X від її МО:
D X M X M X
2
D X x1 M X p1 x2 M X p2 xn M X pn
2
Дисперсія є мірою розсіяння
значень випадкової величини
відносно середнього значення
розподілу.
Більші
значення
дисперсії свідчать про більші
відхилення значень випадкової
величини від центру розподілу.
2
2
Приклад двох сукупностей із
однаковим середнім значенням
але різною дисперсією.
Червоним позначено вибірку із
середнім 100 і дисперсією 100,
а синім показано вибірку із
середнім 100 і дисперсією 2500.
5

6.

Властивості дисперсії дискретної випадкової величини
1)
2
D X M X M X M X 2 2 X M X M 2 X M X 2 2M X M X M 2 X
D X M X 2 M 2 X
M X 2 2M 2 X M 2 X M X 2 M 2 X
2)
D C M C 2 M 2 C C 2 C 2 0
3)
D CX C 2 D X
4)
D X Y D X D Y
D CX M C 2 X 2 M 2 CX C 2 M X 2 C 2 M 2 X C 2 M X 2 M 2 X C 2 D X
2
2
D X Y M X Y M 2 X Y M X 2 2 XY Y 2 M X M Y
M X M
X M Y M
M X 2 2 M X M Y M Y 2 M 2 X 2 M X M Y M 2 Y
2
5)
2
2
2
Y D X D Y
D X Y D X D Y
6

7.

Середнє квадратичне відхилення
Середнє квадратичне відхилення — у теорії ймовірностей один із найпоширеніших показників
розсіювання (розкиду) значень випадкової величини відносно її математичного сподівання, тобто центру
розподілу.
Має ту ж розмірність, що і випадкова величина. В літературі для позначення стандартного відхилення
використовується літера грецької абетки сигма σ:
X D X
За визначенням середнє квадратичне відхилення є квадратним коренем із дисперсії. Як і дисперсія
характеризує розсіяння значень навколо центру розподілу: більшому значенню стандартного відхилення
відповідає більший їх розкид. Практична перевага середнє квадратичного відхилення як міри розсіяння
в порівнянні з дисперсією полягає в тому, що його розмірність збігається з розмірністю випадкової
величини, в той час як розмірність дисперсії — квадрат розмірності випадкової величини.
Іноді середнє квадратичне відхилення називають «стандартною похибкою»
7

8.

ЗАДАЧА ПРО ПОВТОРЕННЯ ВИПРОБУВАНЬ (ДОСЛІДІВ)
Біноміальний розподіл
Постановка задачі: Нехай проводиться n випробувань, причому ймовірність появи події А в кожному випробуванні
дорівнює р і не залежить від результату інших випробувань (незалежні випробування). q = 1 – р.
Знайдемо ймовірність того, що при n випробуваннях подія А настане m раз.
A A...A
A A...A
m раз n m раз
P 5 3
P n m Cnm p m q n m
n!
5!
pm qn m
0,43 0,62 0,2304
m! n m !
3! 2 !
P n m
P 5 4
n!
pm qn m
m! n m !
5!
0,44 0,61 0,0768
4!1!
P 0,2304 0,0768 0,01024 0,31744
Формула Бернуллі
P 5 5
5!
0,45 0,60 0,01024
5! 0 !

9.

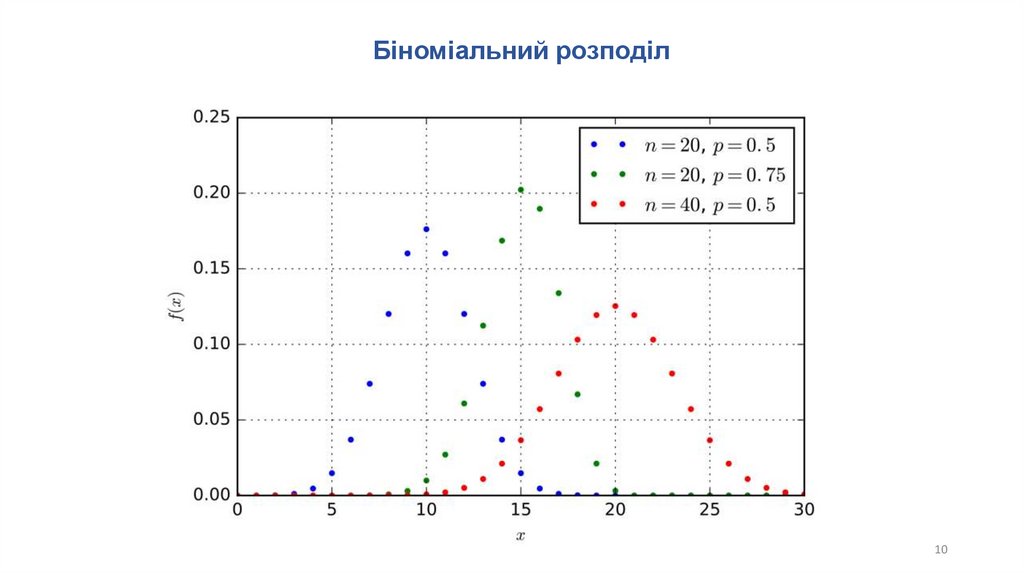
Біноміальний розподіл
Знову розглянемо n незалежних випробувань, в кожному з яких настає подія А з ймовірністю р.
Позначимо через X випадкову величину, рівну числу появ події А в n випробуваннях.
P n m
n!
pm qn m
m! n m !
X
0
1
m
n
P
qn
Cn1 p q n 1
Cnm p m q n m
pn
закон біноміального розподілу
Хi
0
1
М(Х i ) = 0q +1p = p
Pi
q
p
X X1 X 2 X n
X i2
02
12
М( X i2 ) = 02 q + 12 p = p
Pi
q
p
D X i M X i2 M 2 X i p p 2 p 1 p pq
М(Х) =np
D X D X1 D X 2 D X n npq
X npq
9

10.

Біноміальний розподіл
10

11.

Розподіл Пуассона
Постановка задачі: Нехай проводиться серія n незалежних випробувань (n = 1, 2, 3, ...), причому ймовірність появи
цієї події А в цій серії Р(А) = рn > 0 залежить від її номера n і прагне до нуля при n .
прп = μ = const
lim
n
Cnm
m
nlim
n
lim 1
n
n
n m
pn
P n m
n
n n 1 n 2 n m 1
m!n m
Cnm
pnm
1 pn
n m
Cnm
Pn m
m!
m
n m
1
n n
1 2 m 1 m
lim 1 1 1 1
m! n n n
n m!
m
m
n
m
lim 1
1 e 1 e
n
n n
m
e
lim 1 1 x e
x
x
формула Пуассона
11

12.

Розподіл Пуассона
Визначення:
1) Кажуть, що випадкова величина Х визначена за законом Пуассона, якщо ця величина задана таблицею:
*Розподіл Пуассона є граничною формою біноміального розподілу.
k
M X
2
k 0
2
k
k!
e
e
k
k 1
k 1
k 1 !
e
k 1
k 1
k 1
k
k
k
k 1 k 1 ! k 1 k 1 ! k 1 k 1 !
k 1
k 2
e k 1
e e k 1
e 2 e e e e 2
k 1 !
k 2 !
k 2
k 2
D X M X 2 M 2 X 2 2
X
12

13.

Розподіл Пуассона
P
m
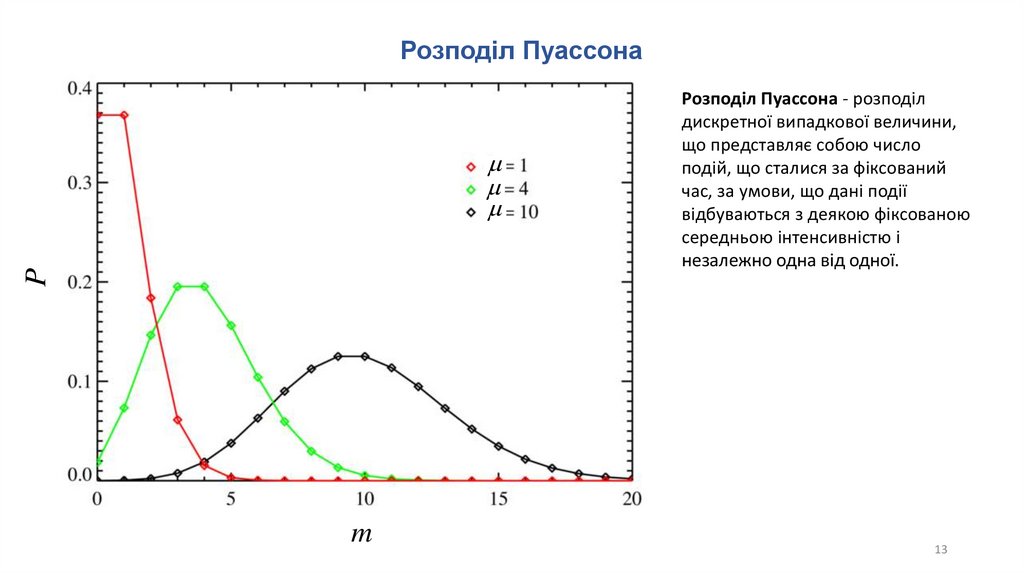
Розподіл Пуассона - розподіл
дискретної випадкової величини,
що представляє собою число
подій, що сталися за фіксований
час, за умови, що дані події
відбуваються з деякою фіксованою
середньою інтенсивністю і
незалежно одна від одної.
13