Микроволновая электроника

1.

СПбГЭТУ «ЛЭТИ»
Кафедра радиотехнической электроники
«Микроволновая
Электроника»
доцент
Иванов Вячеслав Александрович
[email protected]
Слайд № 1 Л3
Микроволновая электроника Л3

2.

План лекции №3
Законы сохранения числа частиц, импульса и энергии
(Взаимодействие потоков заряженных частиц с переменным
электромагнитным полем)
1.4
Законы сохранения числа частиц, импульса и энергии
Временные и пространственные интервалы, характеризующие
движение носителей в разных средах. (Приложение №1 в
Учебнике)
1.5
Особенности взаимодействия подвижных носителей
заряда со статическим полем в вакууме и твердом теле.
Слайд № 2 Л3
Микроволновая электроника Л3

3.

Временные и пространственные интервалы, характеризующие
движение носителей в разных средах (главное)
Приближение времени релаксации. Процессы в природе по exp законам.
n n n0
t
n
n ( 10 cek)
v
t
v vd
p
(W ) 3 k (Te T0 )
t
2 (Te )
p ( p 10 (12....15) cek)
6
n
Время релаксации
импульса
Время жизни
n * vT D n
p * vT
Диффузионная длина - ld
Длина свободного
пробега - l p
(Te )
( 10 (11...13) cek)
Время релаксации энергии
* vT
Длина разогрева
(охлаждения)- l
n Tmicro p
Слайд № 3 Л3
Микроволновая электроника Л3

4.

Временные и пространственные интервалы, характеризующие
движение носителей в разных средах (главное)
Максвелловское время релаксации (заряда) m . Максвелловская частота релаксации m.
Дифференциальная частота максвелловской релаксации md .
t
Из уравнений Максвелла (1и 4)
-проводимость,
Но!!!
d
dv
dE
v / E -подвижность
- дифференциальная
подвижность
Рис.
А.1.1.
дифференциальной
носителей заряда.
К
q n
m
m
t
объяснению
подвижности
m q n
m
!
qn d
md
qn d
Рис. А.1.2. Изменение амплитуды
зарядовой
неоднородности
при
различных параметрах среды..
Зарядовая неоднородность в п/п может нарастать!!!
Слайд № 4 Л3
Микроволновая электроника Л3

5.

Временные и пространственные интервалы, характеризующие
движение носителей в разных средах (главное)
Дебаевский радиус экранирования LD . Плазменная частота Tp .
Как бы мы не считали энергию – результат должен быть один
и тот же.
Wтермодинам Wмеханика Wэлектродинам
mvT
3
kT0
qUT
2
2
2
Рис. А.1.3. К объяснению природы
плазменных колебаний
Найдем распределение потенциала,
используя уравнение Пуассона:
Интегрируя на рассматриваемом промежутке, получим:
или
3 kT0
LD
q2 Nd
и
m
Tp
q2 Nd
LD
2 U T
qN d
dE qN d
dx
Часто используют понятие
плазменная частота:
q2 Nd
p 2
m
Длина Дебая – функция температуры (энергии) электронов и уровня легирования.
Слайд № 5 Л3
Микроволновая электроника Л3

6.

Законы сохранения числа частиц, импульса и энергии
Функция распределения
Пример: Функция
распределения Максвелла
f (r, p, t )
3/2
m
f ( v) n
e
2 kTe
r, p,t
mv2
kTe
,
фазовое
пространство
Интегральные параметры через функцию распределения
n(r, t ) f (r, p, t )dP.
P
(r, t ) q f (r, p, t )dP
P
q
J (r, t ) p f (r, p, t )dP.
m P
Теорема Лиувилля: функция распределения остается постоянной
вдоль любой траектории в фазовом пространстве, т.е.
df (r, p, t )
0
dt
Слайд № 6 Л3
df (r, p, t ) f f dr f dp
0
dt
t r dt p dt
Микроволновая электроника Л3

7.

Кинетическое уравнение Больцмана (Власова)
Для вакуумного случая (гидродинамический подход):
dr
v
dt
dp
F
dt
f
v r f F p f 0
t
уравнение Власова
Если есть процессы рассеяния, то правая часть ненулевая, т.е.:
для плазмы твердого тела (гидродинамический подход):
f
f
v r f F p f
t
t с
Кинетическое Уравнение Больцмана (КУБ)
Слайд № 7 Л3
Микроволновая электроника Л3

8.

Законы сохранения числа частиц, импульса и энергии
Преобразуем КУБ, учитывая, что у скорости 2 компоненты:
дрейфовая и тепловая
u 0
v vd u
1. Проинтегрируем КУБ по пространству импульсов, получим закон
сохранения числа частиц:
n / t (n v d ) G R
2. Умножение КУБ на v с последующим интегрированием по
пространству скоростей дает уравнение переноса, или уравнение
сохранения потока импульса частиц :
Pˆ nm vv
Pˆ
(mnv d ) / t Pˆ nq(E v B) nFir ,
плотность потока импульса,
пространственная расходимость
потока импульса;
Слайд № 8 Л3
тензорное произведение двух
векторов, называемое диадой.
сила
nFir результирующая
внутреннего «трения».
vv
Микроволновая электроника Л3

9.

Законы сохранения числа частиц, импульса и энергии
3. Умножение КУБ на v и интегрирование по всему пространству
скоростей дает уравнение сохранения энергии:
2
(nW ) t q jE nQ
W mv 2 3kTe 2
2
d
q W vd
полная энергия частицы: сумма энергии направленного дрейфа частицы и тепловой энергии
поток полной энергия частицы
jE
джоулево тепло
Q
Слайд № 9 Л3
изменение энергии
за счет процессов рассеяния
Микроволновая электроника Л3

10.

Законы сохранения числа частиц, импульса и энергии
(в приближении времени релаксации)
Временные и пространственные интервалы, характеризующие процесс переноса носителей заряда
;
Самостоятельно. Приложение 1.
n
n n0
(n v d )
t
n
Уравнение сохранения числа частиц
v
1 kTe q
v vd
( v ) v
n (E v B )
t
n m m
p
Уравнение сохранения потока импульса частиц
(nW )
3 nk (Te T0 )
q jE
t
2 (Te )
Уравнение сохранения энергии
Слайд № 10 Л3
Микроволновая электроника Л3

11.

Законы сохранения числа частиц, импульса и энергии
(частные случаи)
;
Вакуум
n
(n v d ) 0
t
v q
(E v B )
t m
(nmv 2) t jE
2
Слайд № 11 Л3
Микроволновая электроника Л3

12.

Законы сохранения числа частиц, импульса и энергии
(частные случаи)
Твердое тело
,
n
n n0
(n v d )
t
n
kTe n q
v
E
m n m
p (Te )
3 nk (Te T0 )
jE
2 (Te )
;
e
kTe
n
v p (Te )E
p (Te )
m
m
n
n
(Te )E D(Te )
n
(Te T0 ) f (E)
«Горячие» электроны
Слайд № 12 Л3
Микроволновая электроника Л3

13.

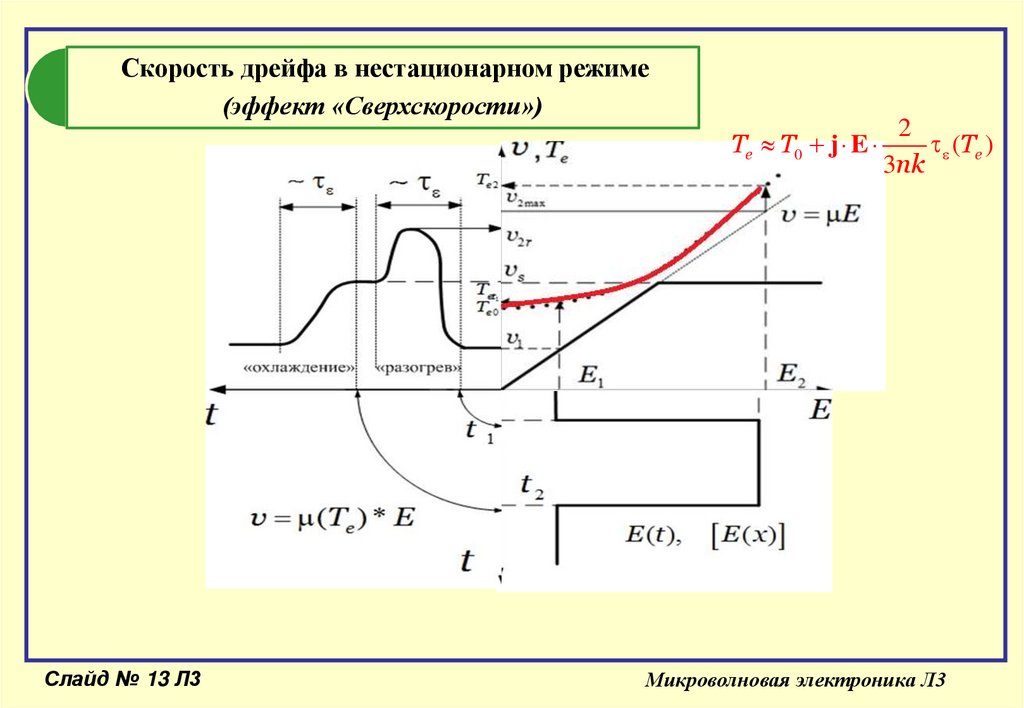
Скорость дрейфа в нестационарном режиме
(эффект «Сверхскорости»)
Te T0 j E
Слайд № 13 Л3
2
(Te )
3nk
Микроволновая электроника Л3

14.

Скорость дрейфа в нестационарном режиме
(эффект «Сверхскорости»)
Изменение скорости в арсениде галлия
при воздействии импульса электрического
поля. (Метод крупных частиц)
Слайд № 14 Л3
Изменение скорости в арсениде галлия
(Эксперимент)
Микроволновая электроника Л3

15.

Анализ уравнения для мощности взаимодействия
• 1. «Очертания» пространства взаимодействия. (Типовые элементы
приборов, зазор взаимодействия).
• 2. Наведенный ток, теорема Шокли-Рамо.
• 3. Угол пролета, коэффициент взаимодействия.
• 4. Токи в пространстве взаимодействия.
«Некоторые понятия трудны для понимания не потому они сложны,
а потому, что не входят в круг наших понятий»
Козьма Прутков
Слайд № 15 Л3
Микроволновая электроника Л3

16.

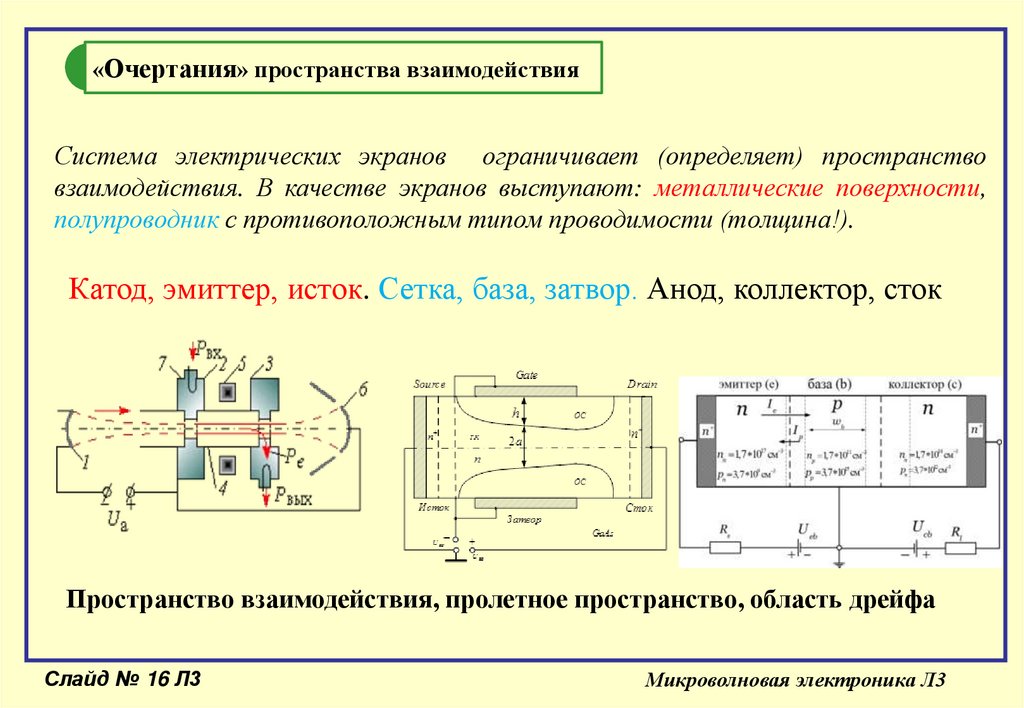
«Очертания» пространства взаимодействия
Система электрических экранов ограничивает (определяет) пространство
взаимодействия. В качестве экранов выступают: металлические поверхности,
полупроводник с противоположным типом проводимости (толщина!).
Катод, эмиттер, исток. Сетка, база, затвор. Анод, коллектор, сток
Пространство взаимодействия, пролетное пространство, область дрейфа
Слайд № 16 Л3
Микроволновая электроника Л3

17.

P J ( , v (E)) E( )dV
V
Одномерный случай,
переменное (во времени) и постоянное поле, переменный и постоянный токи.
j j 0 j 0 v v0 v
d
E E0 E
d
P ( j 0 j )( E0 E )dx ( j 0 E0 j 0 E j E 0 j E )dx
0
0
d
P0 j 0 E0dx
0
d
Ускорение потока
P ( j 0 E j E0 )dx
0
d
P ( j E )dx
0
Слайд № 17 Л3
P0 0
замедление
За период гармонического взаимодействия
Модуляция скорости
P0 0
P 0
модуляция плотности
Мощность взаимодействия модулированного
потока с переменным полем
За период гармонического взаимодействия
P 0
Микроволновая электроника Л3

18.

Из Уравнения сохранения энергии (см. Л3)
(nW )
3 nk (Te T0 )
q jE
t
2 (Te )
Взаимодействие в вакууме
T
(nmv 2) JEdt 0,
2
0
Взаимодействие в полупроводниках
3 nk (Te T0 )
n (mv 2 3kTe 2) JEdt
dt
0
0 2
(Te )
T
2
d
T
T
Как найти
JEdt ?
0
E - поле, созданное током J
«Самосогласованное» поле.
Слайд № 18 Л3
Микроволновая электроника Л3

19.

Наведенный ток
На экранирующих поверхностях наводятся заряды противоположного знака.
При движении свободных зарядов – движутся и наведенные, образуя так называемый
наведенный ток.
J tot J
D
t
J tot 0.
dE
dE
Jtot v
Jk
dt
dt
По пространству взаимодействия d
d
J tot
d
1
1 dE
J
dx
dx J н J см
k
d0
d 0 dt
d
1
J н J k dx
d0
наведенный ток
(плотность тока).
Мощность взаимодействия для однородного распределения поля по пространству взаимодействия
и гармоническом законе изменения во времени
d
d
d
U
(I н Zr )
(I н Zr )
Pэл AJ k (x) dx (AJ k ( x)
)dx
AJ k ( x)dx I н Z r ( I н )
d
d
d 0
0
0
«Самосогласованное» поле.
Слайд № 19 Л3
Микроволновая электроника Л3

20.

Другой вариант вывода
формулы для наведенного тока
Теорема Шокли-Рамо
q
q1n
v
e1
q2n
mA
in
U 1 В
in q(e1 v)
dr
dA Fdr qEdr qE dt qEvdt ,
dt
dA inUdt .
E
in q v q(e1v),
U
Теорема Шокли-Рамо
Слайд № 20 Л3
Микроволновая электроника Л3

21.

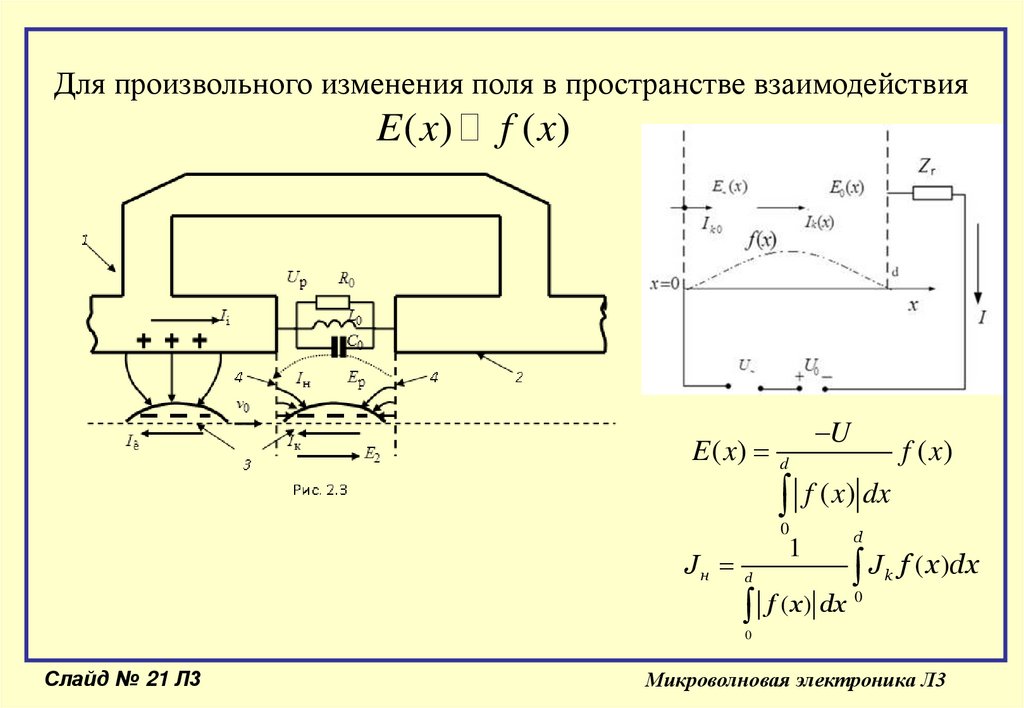
Для произвольного изменения поля в пространстве взаимодействия
E ( x)
f ( x)
E ( x) d
U
f ( x)
f ( x) dx
0
Jн d
1
d
J f ( x )dx
f ( x ) dx 0
k
0
Слайд № 21 Л3
Микроволновая электроника Л3

22.

Угол пролета, коэффициент взаимодействия
d
Время пролета 0 пр
v0
сравним с периодом микроволновых
колебаний
d
0 пр
v0
1 d пр
Tmicro Tmicro 2 v0
2
d
1
I н ( I k 0e
d0
j
x
v0
Tmicro
0 пр
d
пр 2
Tmicro v0
Угол пролета
sin( 0 2) j 0 2
)dx I k 0
e
0 2
(если конвекционный ток изменяется только по фазе)
Слайд № 22 Л3
(Теория подобия)
sin( 0 2)
M
0 2
Коэффициент взаимодействия
Микроволновая электроника Л3

23.

Hard work, big results
"Think big, act big, believe big and the results will be
big".
Слайд № 23 Л1
Микроволновая электроника Л1