Чертеж плоскости в системе прямоугольных проекций. Классификация плоскостей

1.

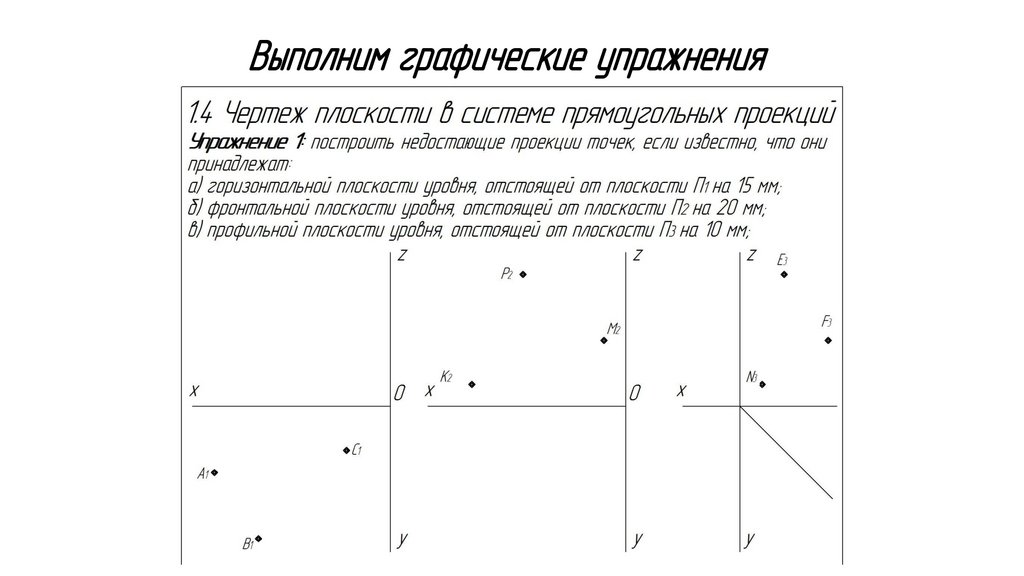
Чертеж плоскости в системе
прямоугольных проекций.
Классификация плоскостей

2.

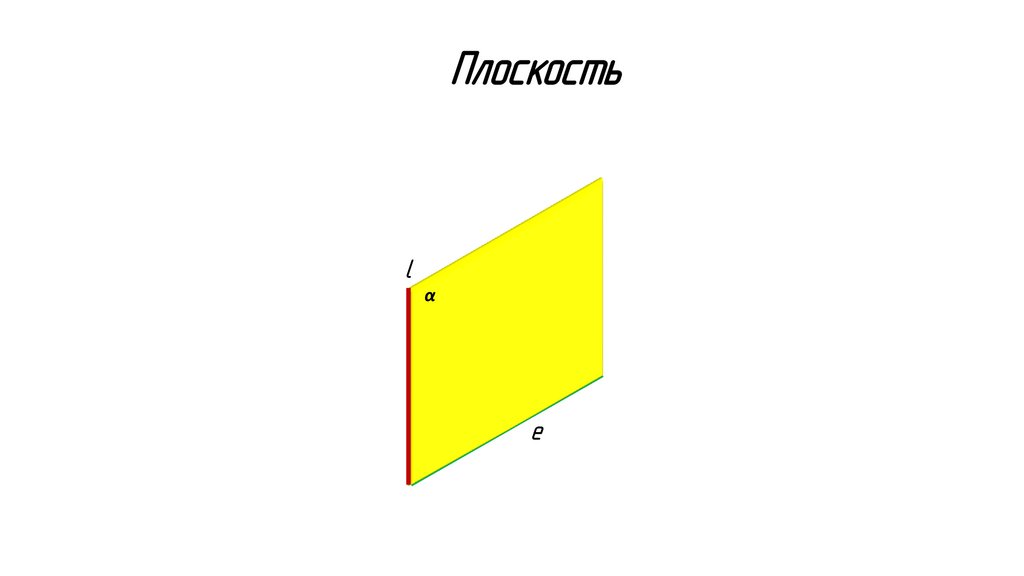
Плоскость
l
α
e

3.

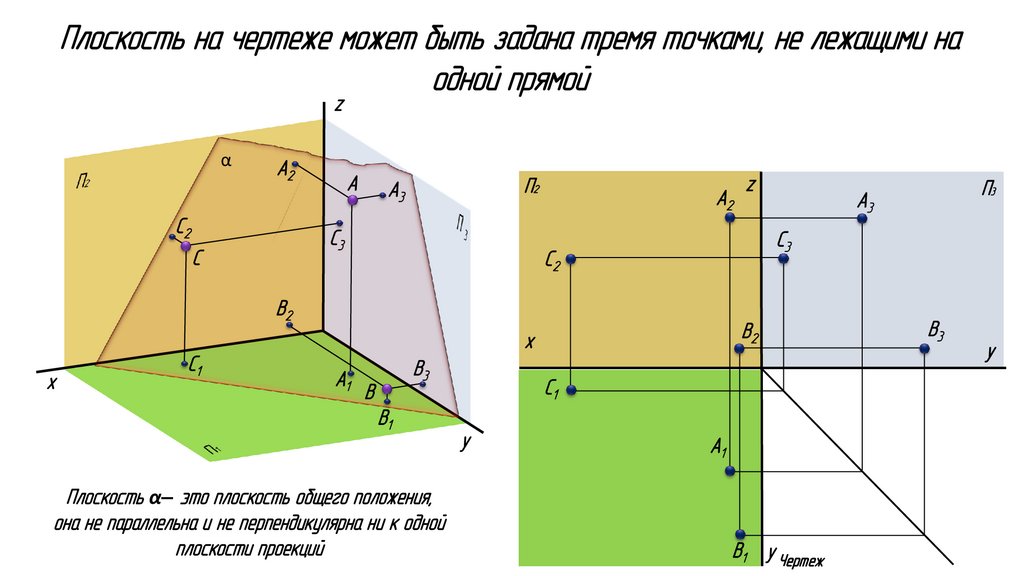
Плоскость на чертеже может быть задана тремя точками, не лежащими на
одной прямой
z
α
A2
С2
A
П2
A3
С3
С
A2
С2
B2
х
х
A1
В3
B
B1
Плоскость α– это плоскость общего положения,
она не параллельна и не перпендикулярна ни к одной
плоскости проекций
С1
y
A1
A1
С1
П1
П3
A3
С3
B2
С1
z
B1
B1 y y Чертеж
В3
y

4.

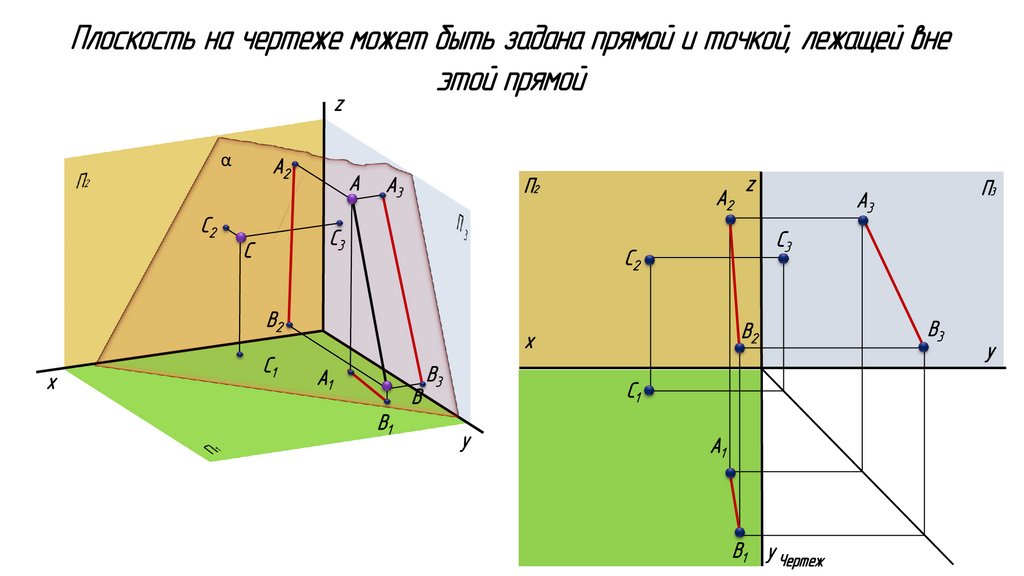
Плоскость на чертеже может быть задана прямой и точкой, лежащей вне
этой прямой
z
α
A2
С2
A
A3
П2
С3
С
х
B2
х
A1
B
B1
В3
СA1 1
y
A1
С1
П1
П3
A3
С3
С2
B2
С1
A2
z
B1
B1 y y Чертеж
В3
y

5.

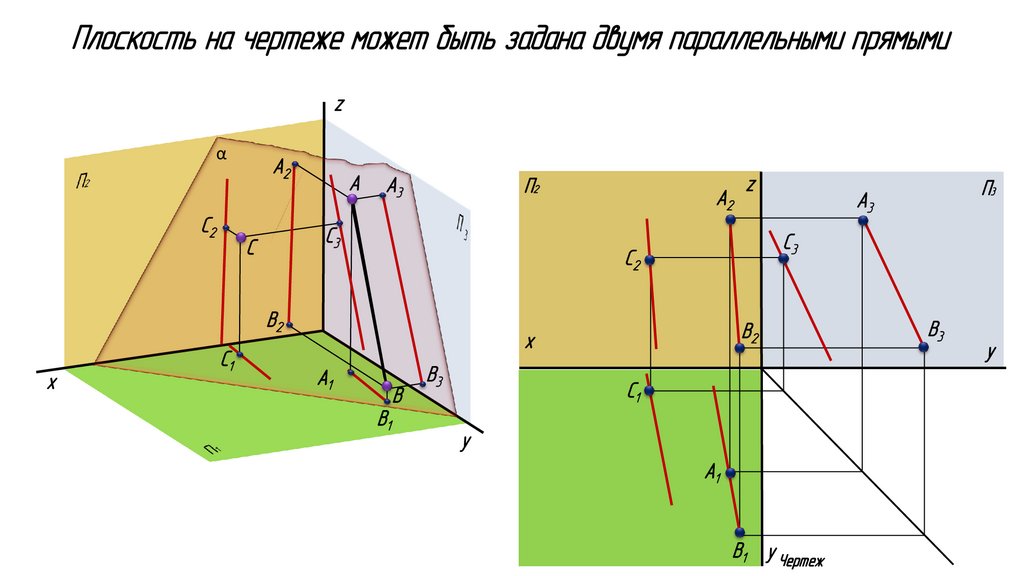
Плоскость на чертеже может быть задана двумя параллельными прямыми
z
α
С2
A2
A
A3
П2
С3
С
х
B2
х
A1
B
B1
В3
СA1 1
y
A1
С1
П1
П3
A3
С3
С2
B2
С1
A2
z
B1
B1 y y Чертеж
В3
y

6.

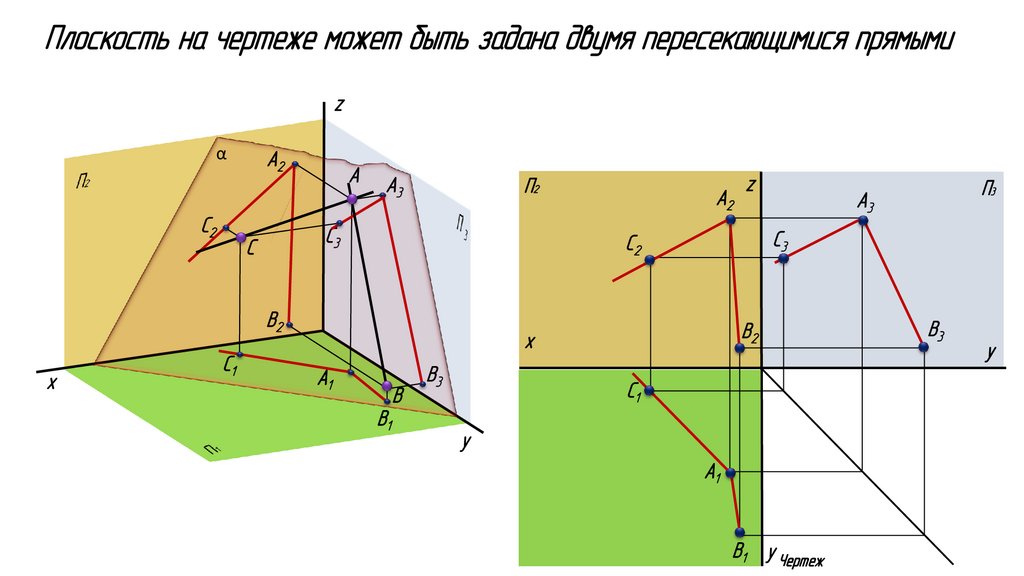
Плоскость на чертеже может быть задана двумя пересекающимися прямыми
z
α
С2
A2
A
A3
П2
С3
С
х
B2
х
A1
B
B1
В3
СA1 1
y
A1
С1
П1
П3
A3
С3
С2
B2
С1
A2
z
B1
B1 y y Чертеж
В3
y

7.

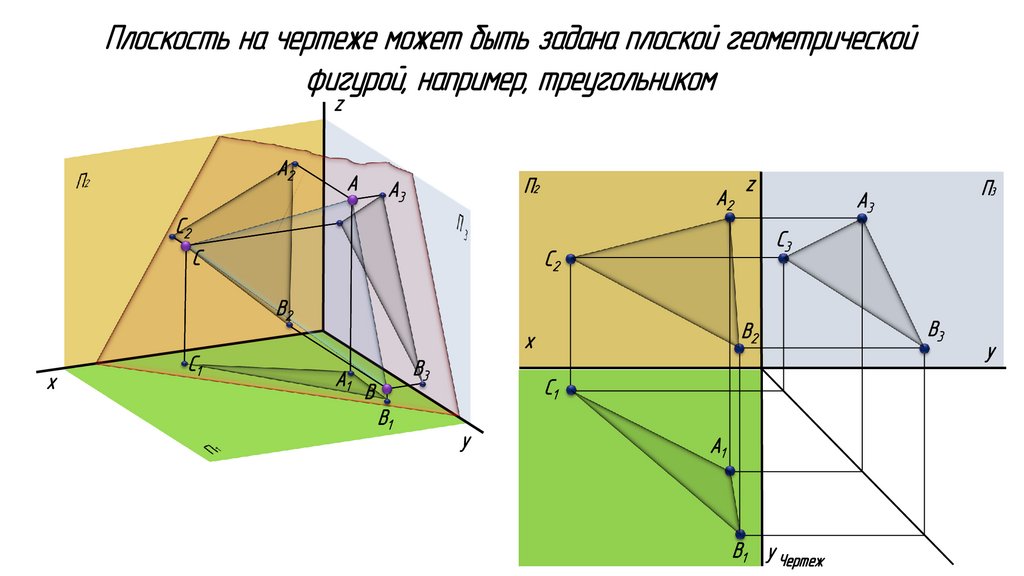
Плоскость на чертеже может быть задана плоской геометрической
фигурой, например, треугольником
z
A2
A
П2
A3
A2
z
С2
С
С3
С2
B2
B2
х
х
С1
A1
В3
B
B1
С1
y
A1
A1
С1
П1
П3
A3
B1
B1 y y Чертеж
В3
y

8.

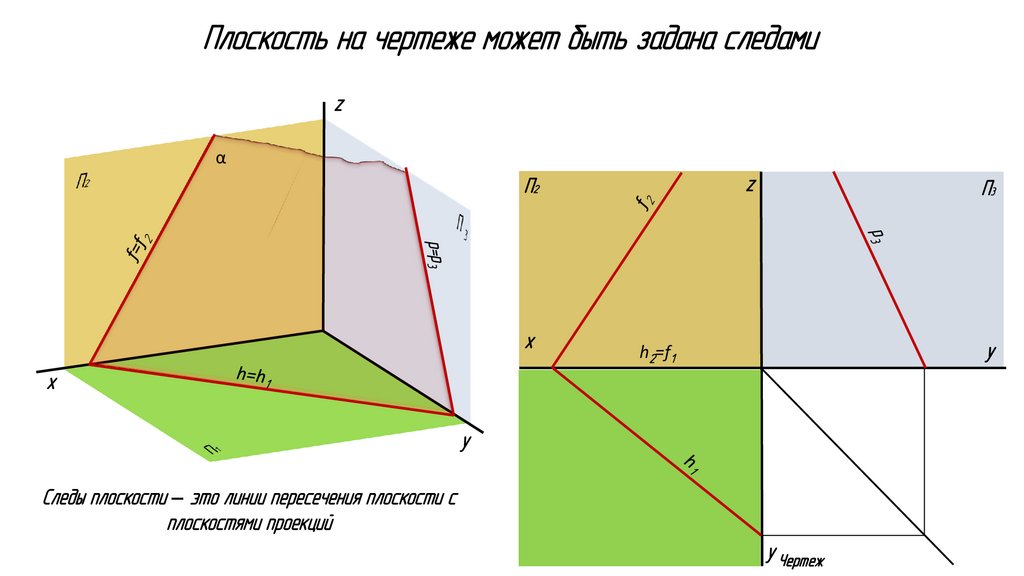
Плоскость на чертеже может быть задана следами
z
α
z
П2
х
y
h2=f1
A1
х
y
Следы плоскости – это линии пересечения плоскости с
плоскостями проекций
С1
П1
П3
B1
y y Чертеж

9.

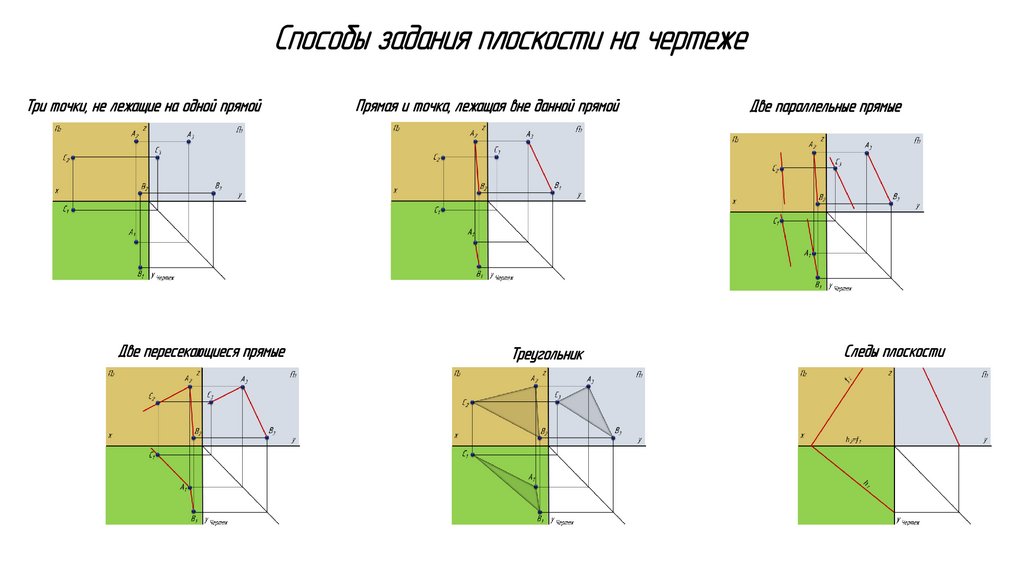
Способы задания плоскости на чертеже
Три точки, не лежащие на одной прямой
Две пересекающиеся прямые
Прямая и точка, лежащая вне данной прямой
Треугольник
Две параллельные прямые
Следы плоскости

10.

Плоскости частного положения
Проецирующие плоскости

11.

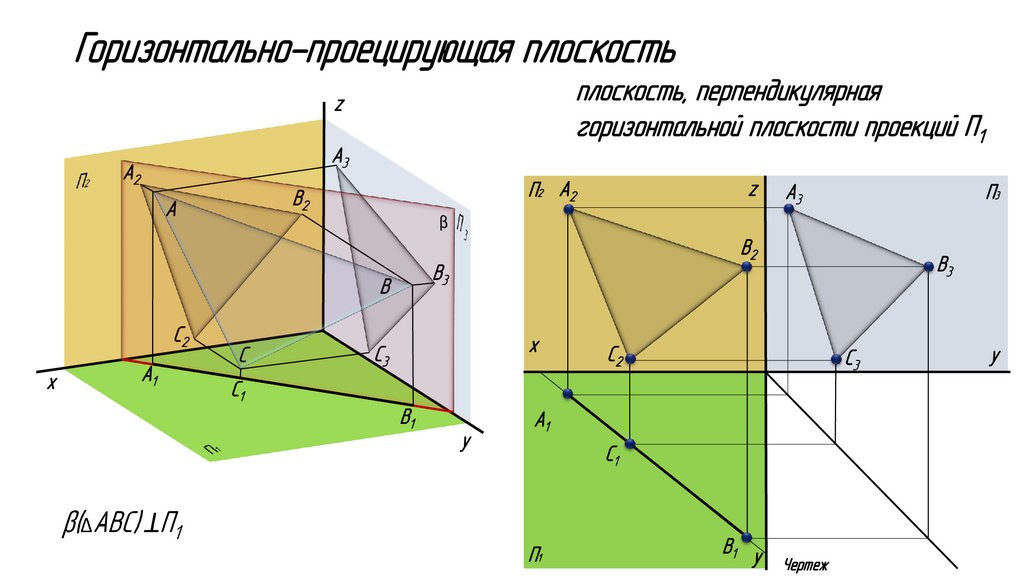
Горизонтально-проецирующая плоскость
плоскость, перпендикулярная
горизонтальной плоскости проекций П1
z
A3
A2
A
z
П2 A2
B2
A3
П3
B2
B
С2
х
A1
С
В3
B3
х
С3
С2
С3
С1
B1
y
A1
С1
П1
B1 y
Чертеж
y

12.

Фронтально-проецирующая плоскость
плоскость, перпендикулярная
фронтальной плоскости проекций П2
z
A2
х
х
С
С1
A1
В3
B2
B
B1
A3
α
B3
С2
П3
A2
A3
A
B2
z
П2
С2
С3
С3
B1
y
A1
П1
С1
y
Чертеж
y

13.

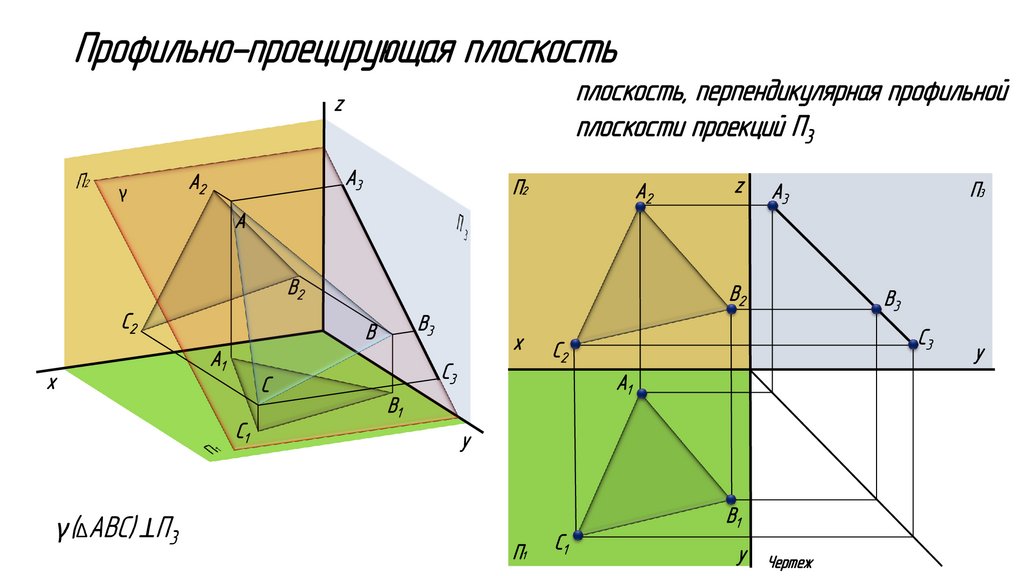
Профильно-проецирующая плоскость
плоскость, перпендикулярная профильной
плоскости проекций П3
z
γ
A3
A2
П2
A2
z
П3
A3
A
B2
С2
х
B2
В3
B
A1
х
С3
С
С3
С2
A1
B1
С1
В3
y
B1
П1
С1
y
Чертеж
y

14.

Плоскости частного положения
Плоскости уровня

15.

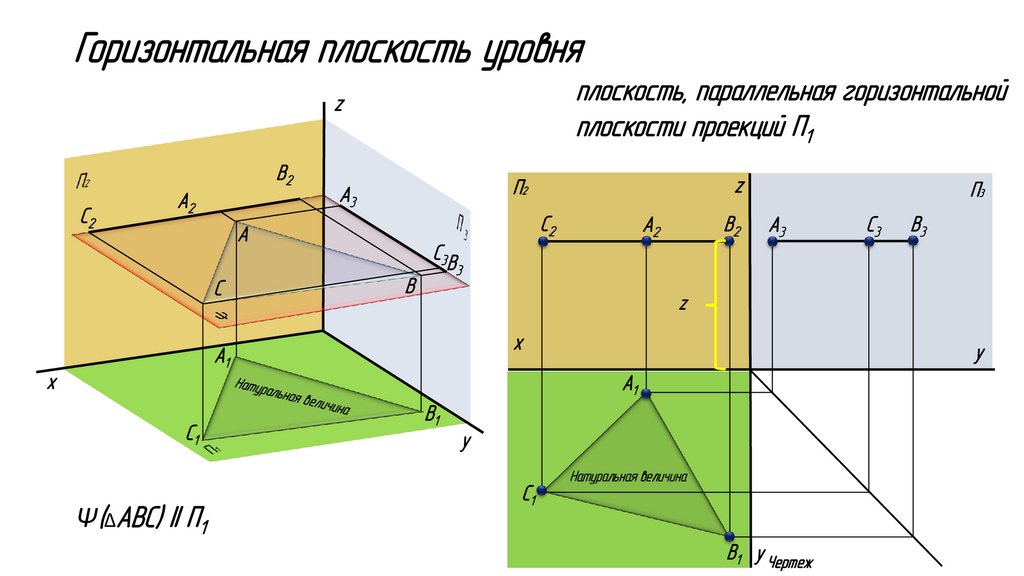
Горизонтальная плоскость уровня
плоскость, параллельная горизонтальной
плоскости проекций П1
z
B2
С2
A2
С2
A
С
z
П2
A3
B2
A2
П3
A3
3
B
z
х
х
y
A1
B1
y
Натуральная величина
Ψ(∆ABC) II П1
В3
С3В
A1
С1
С3
СС11
П1
B1
B1y y Чертеж

16.

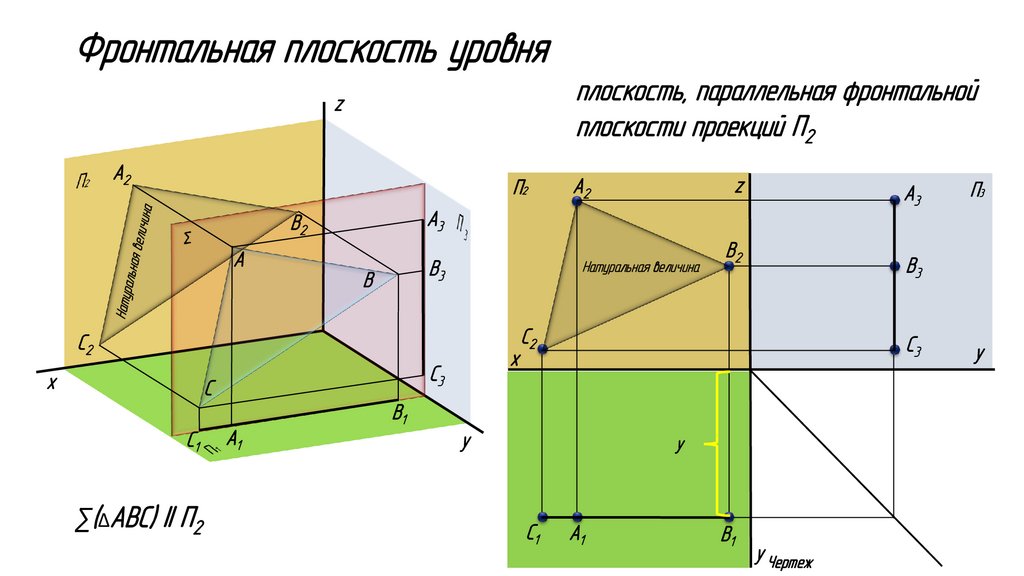
Фронтальная плоскость уровня
плоскость, параллельная фронтальной
плоскости проекций П2
z
A2
П2
A
В3
B
Натуральная величина
С2
х
С3
С
B2
С2
∑(∆ABC) II П2
A1
П3
A1
y
y
С1
С1
П1
В3
С3
B1
С1
A3
A3
B2
х
z
A2
A1
B1
y y Чертеж
y

17.

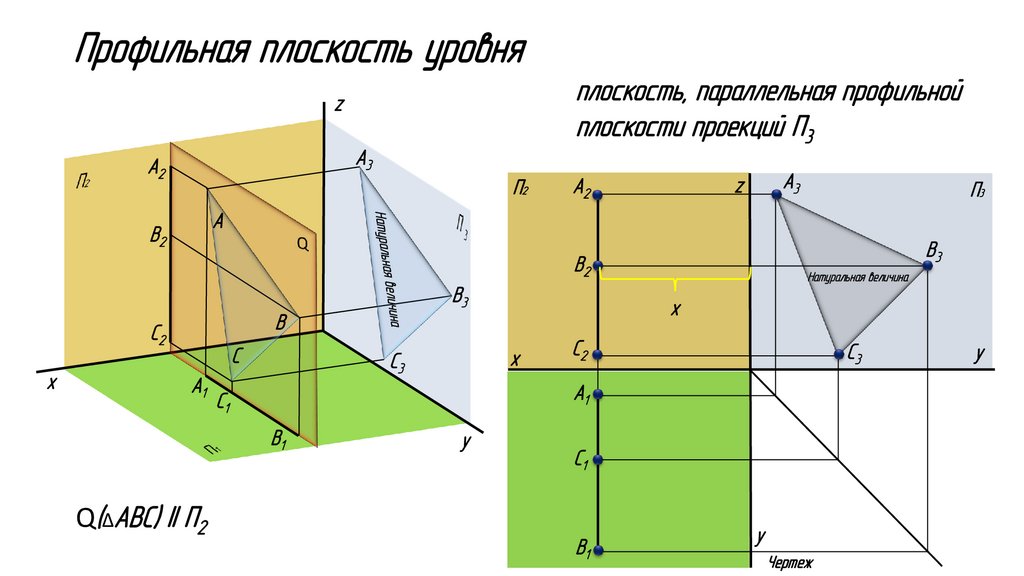
Профильная плоскость уровня
плоскость, параллельная профильной
плоскости проекций П3
z
A3
A2
П2
A3
z
A2
A
B2
В3
B2
Натуральная величина
В3
x
В
С2
х
П3
С
A1
A1
С1
B1
Q(∆ABC) II П2
С2
х
С3
y
С3
A1
С1
С1
П1
B1
y
y
Чертеж
y

18.

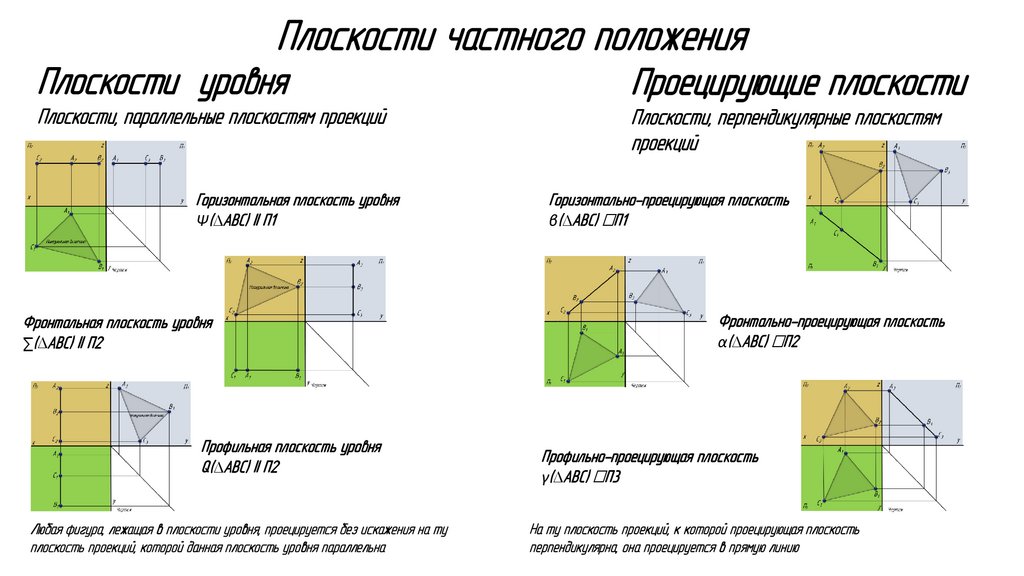
Плоскости частного положения
Плоскости уровня
Проецирующие плоскости
Плоскости, параллельные плоскостям проекций
Плоскости, перпендикулярные плоскостям
проекций
Горизонтальная плоскость уровня
Ψ(∆ABC) II П1
Фронтальная плоскость уровня
∑(∆ABC) II П2
Профильная плоскость уровня
Q(∆ABC) II П2
Любая фигура, лежащая в плоскости уровня, проецируется без искажения на ту
плоскость проекций, которой данная плоскость уровня параллельна
Горизонтально-проецирующая плоскость
β(∆ABC) ꓕП1
Фронтально-проецирующая плоскость
α(∆ABC) ꓕП2
Профильно-проецирующая плоскость
γ(∆ABC) ꓕП3
На ту плоскость проекций, к которой проецирующая плоскость
перпендикулярна, она проецируется в прямую линию

19.

Выполним графические упражнения