Алгоритм разложения ФКП в ряд Лорана

1.

Типовой расчет №1 (Модуль №2)
7. Разложить функцию f(z) в ряд Лорана в области D
или в окрестности т. z0.
8. Найти все особые точки функции f(z ), определить
их характер (для полюсов указать их порядок).
9. Исследовать функцию f(z) в окрестности
бесконечно удаленной точки.
10. Найти вычеты функции f(z) относительно каждого
из ее полюсов.
11. Вычислить заданный интеграл.

2.

Таблица 3. Задания 7-10 к модулю №2 Вар. 1-7

3.

Таблица 3. Задания 7-10 к модулю №2 Вар. 8-12

4.

Таблица 4. Задание 11 к модулю №2 Вар. 1-12
Вариант
Интеграл
Вариант
1 x2
1 x 4 dx
1
7
2
1
(1 x 2 ) 3 dx
3
e z dz
C z 3 ( z 1) ; C : z 2
4
zdz
C z 2 3; C : z 1 4
5
sin zdz
C z 2 z ; C : z 3
6
tgz dz; C : z 2
C
Интеграл
8
dx
2 2
(1 x )
dz
C z(e z 3) ; C : z 4
9
zdz
C 1 2 sin 2 z ; C : z 2
10
e dz
C z 2 z ; C : z 4
z
11
12
x2 1
( x 2 4)( x 2 9) dx
zdz
C 1 z 2 ; C : z 2

5.

Алгоритм разложения ФКП в ряд Лорана
1. Найти особые точки функции
2. Указать центр разложения, область аналитичности
3. Записать общий вид ряда Лорана в заданной области
4. Разложить дробно-рациональную функцию на сумму
простых дробей
5. Каждую дробь представить в виде ряда, используя
формулу суммы бесконечно убывающей
геометрической прогрессии, с учетом области
аналитичности функции
6. Записать разложение функции как сумму этих рядов
и сверить с видом ряда Лорана в п.3
7. Записать ответ согласно п.6

6.

Пример. Разложить функцию в ряд Лорана в указанной области
f ( z)
z
;
2
z 3z 2
D : 2 z 1 3
1. Особые точки z 2 3z 2 0; z1 1; z2 2
2. Область аналитичности, центр разложения
y
Кольцо r z z0 R; 2 z 1 3;
центр z0 1; r 2; R 3 см. Рис.1
3. Общий вид ряда Лорана (в кольце)
k 0
правильная часть
C k
k
k 1 z 1
2 z 1 3
главная часть
4. Разложение на простые дроби
f ( z)
1
f ( z ) Ck z 1
k
4 3 1
z
z
A
B
z 2 3z 2 ( z 1)( z 2) z 1 z 2
z A( z 2) B( z 1);
A 1; B 2
Рис.1
2
x

7.

Пример. Разложение ФКП в ряд Лорана (продолжение)
1
2
f ( z)
f1 ( z ) f 2 ( z )
z 1 z 2
5. Каждую дробь представим в виде ряда, по формуле суммы
бесконечно убывающей геометрической прогрессии, с учетом
области аналитичности Кольцо 2 z 1 3
1
S b1 q S b1
; q 1
1 q
k 0
k
f1 ( z )
1
1
z 1
( z 1) 2
1
2
( z 1) 1
z 1
1
1
2
( z 1)
1
z 1
1
2k
2 k 1
2
k 1
k
( z 1) k 0 z 1
k 0 ( z 1)
k 1 ( z 1)
k

8.

Пример. Разложение ФКП в ряд Лорана (окончание)
S b1 q k S b1
k 0
f 2 ( z)
1
; q 1;
1 q
2
2
z 2 ( z 1) 3
кольцо 2 z 1 3
2
2
1
3 z 1
z 1
3 1
1
3
3
2 z 1
( z 1) k
2
k
2
(
z
1
)
k 1
k 1
3 k 0 3
3
3
k 0
k 0
k
6. Разложение функции как сумма рядов
2
2 k 1
k
(
z
1
)
f ( z) f1 ( z) f 2 ( z)
k 1
k
3
(
z
1
)
k 0
k 1
главнаячасть
прав ильнаячасть
соответствует общему виду ряда Лорана в кольце
2k 1
2
k
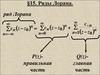
7. Ответ: f ( z )
(
z
1
)
k
k 1
(
z
1
)
3
k 1
k 0