Похожие презентации:
Лекция 14. Метод перевала
1. Лекция 14
§22. Метод перевала.Метод вычисления асимптотических
разложений интегралов по кривой на
комплексной плоскости
аналитических ФКП, зависящих от
действительного параметра.
2.
f zF e
z dz; 1.
C
Асимптотическое разложение в
окрестности точки x0
N
f x k x RN 1 x ;
k 0
k 1 x o k x ;
RN 1 x o N x
3.
При x0 достаточно часто вкачестве (x) выбираются обратные
степени x:
N c
f x k RN 1 x ;
k
k 0 x
1
RN 1 x o
N
x
;
и часто RN 1 x
c N 1
x N 1
4.
Замечание. Асимптотический ряд,вообще говоря, не сходится.
t2
f t
F e
t dt ; 1.
t1
для достаточно гладких f( t ) и ( t )
при условии ! глобального максимума
f( t ) на [ t1; t2 ] :
f( t0 ) > f( t ), f ‘ ( t0 )=0, f "( t0 ) < 0
5. Формула Лапласа
2f t 0
3 / 2
F e
t 0 O
f '' t0
Обобщим этот результат на случай
интегралов от аналитических ФКП.
6.
f zF e
z dz; 1.
C
C g , f z , z C
f z u x , y iv x , y
e
g
i v x , y
1
осциллирующая часть
i v x , y
e
подынтегральной функции
7.
Max. вклад в интеграл даст тотучасток C, на котором u( x, y )
достигает глобального max на С.
Пусть z0- единственная точка
глобального max. u( x , y ) на С:
u( x0, y0 ) > u( x, y )| C.
8.
Cz0
g
g
'
9.
u=0, z g', и в силу принципа max.гармонической функции,
max u| g > u(x , y)|(x,y) g'=>
хотя z0 С точка глобального max
u(x,y) на С, но в окрестности g' точки
z0 точки С, в которых
u( x , y ) > u( x0, y0)
10.
=> Через z0 С проходят другиенаправления на которых u( x, y )
возрастает от значения u( x0, y0 ).
Точка z0=x0+iy0 - седловая точка, или
точка перевала поверхности u( x, y ).
=> название метода.
11.
Max. вклад в интеграл будет даватьучасток интегрирования в
окрестности точки z0, если на нем
u( x, y ) будет убывать с наибольшей
скоростью от значения u( x0, y0 ).
По т. Коши контур С в окрестности
точки z0 С можно деформировать, не
меняя значения интеграла.
12.
Участок С, проходящий через z0 можнонаправить по направлению
наибыстрейшего спуска на
поверхности u( x , y ).
Это направление определяется
направлением u ( z0 ).
13.
Но u v = ux vx + uy vy=0( условия Коши-Римана ).
=> Направление наибыстрейшего
спуска- направление v=0,
т.е линия уровня
v (x , y) = v( x0, y0 ) = const.
14.
Max. вклад в интеграл даетинтегрирование по участку С,
проходящему через z0 и совпадающему
c
v ( x , y ) = v ( x0, y0 ) = const.
Как ведет себя f ( z ) на этом участке?
15.
f z u x , y C iv x , y C'
z0- точка глобального max. =>
v x , y C 0; u x0 , y0 0;
=> f ‘ ( z0 ) = 0 (производная не зависит
от направления).
v x , y C 0; u z0 0 f z0 0
'
16. Найдем направление наибыстрейшего спуска.
1 ''3
2
f z f z0 f z0 z z0 O z z0
2
1 ''
i
i
f z0 ke ; z z0 re
2
3
u x , y u x0 , y0 kr cos 2 O r
2
3
v x , y v x0 , y0 kr sin 2 O r
2
17.
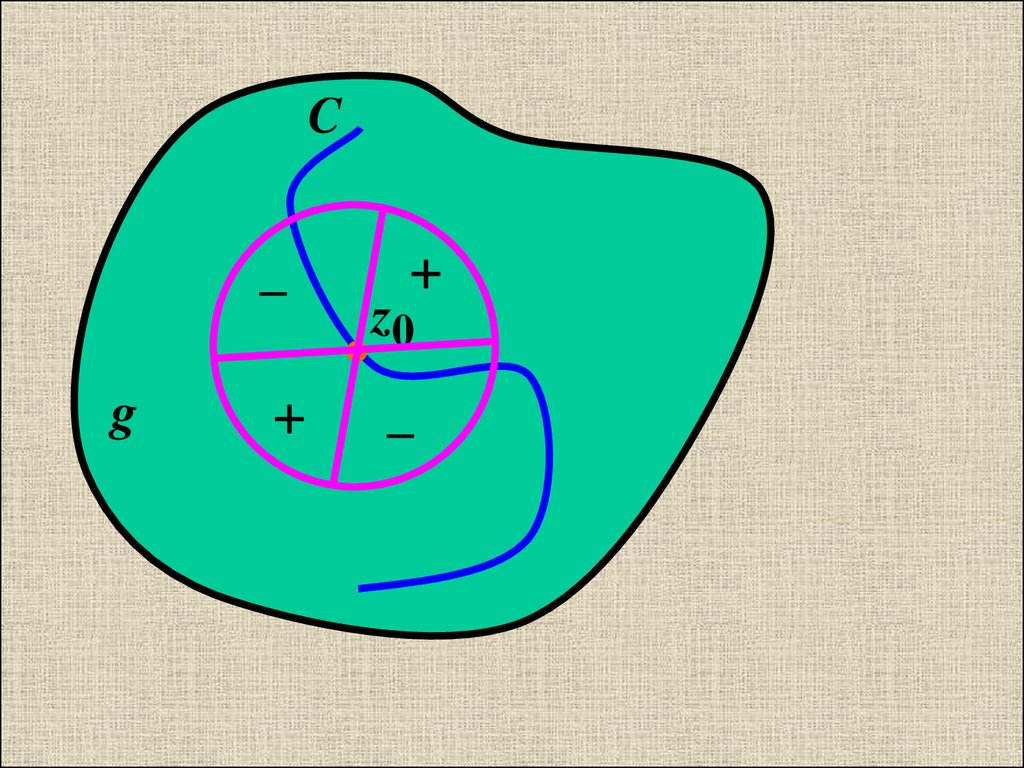
При 0 2 cos( +2 )=0 4 раза =>окрестность точки z0 разбивается на 4
сектора- 2 “+” : cos( +2 )>0,
и два “-”: cos( +2 )<0.
Кривая С должна в точке z0
переходить из одного “-” сектора в
другой “-”.
18.
Cg
z0
19.
Направление наибыстрейшего спускаопределяется условием
cos( +2 ) = -1 => +2 0= ; 0=( - )/2,
где f ’’ (z0)=2kei , = arg f ’’ (z0).
20. Вычислению первого члена асимптотики
f zF e
z dz
C
e
i v z 0
u z
e
z dz ,
C
v x , y C const .
21.
Параметризуем контуринтегрирования С :
z z t z0 te
i 0
; z0 z 0 .
dz
i 0
t t1 , t 2 , dz dt e dt ;
dt
U t u x t , y t ; t x t , y t
U 0 U t ; U 0 0;
'
22.
t2~
dz
U t
F e
t dt
dt
t
1
Выполнены все условия
применимости формулы Лапласа
2
~
dz
U 0
F e
0
'
'
dt t 0
U t0
3 / 2
O
23.
U 0 u x0 , y0 ; 0 z0V t C const V t 0
''
C
2
d ' dz
U 0
f z t t 0 f z
2
dt
dt t 0
dt
d
''
'' dz 2
' d 2z
f z
f z
2
dt
dt t 0
t 0
2
dz
'
''
f z0 0 f z0
dt t 0
24.
dz 2?
dt t 0
z z0 te
i 0
; 2 0
dz
i 0 dz
e ,
1;
dt t 0
dt t 0
dz 2
i 2 0
e
dt t 0
25.
f''
z0 2ke
i
f
''
z0 2 k
2
dz
''
''
i i 2 0
U 0 f z0
2ke e
dt t 0
2ke
i 2 0
2ke
i
2 k f
''
z0
26.
2f z0
i 0
F e
z0 e
''
f z0
3 / 2
O
0
2
; arg f
''
z0 .
27.
1, f z0 0'
2
f z0
i 0
F e
z0 e
''
f z0
3 / 2
O
0
2
; arg f
''
z0 .
Знак определяется направлением
интегрирования.

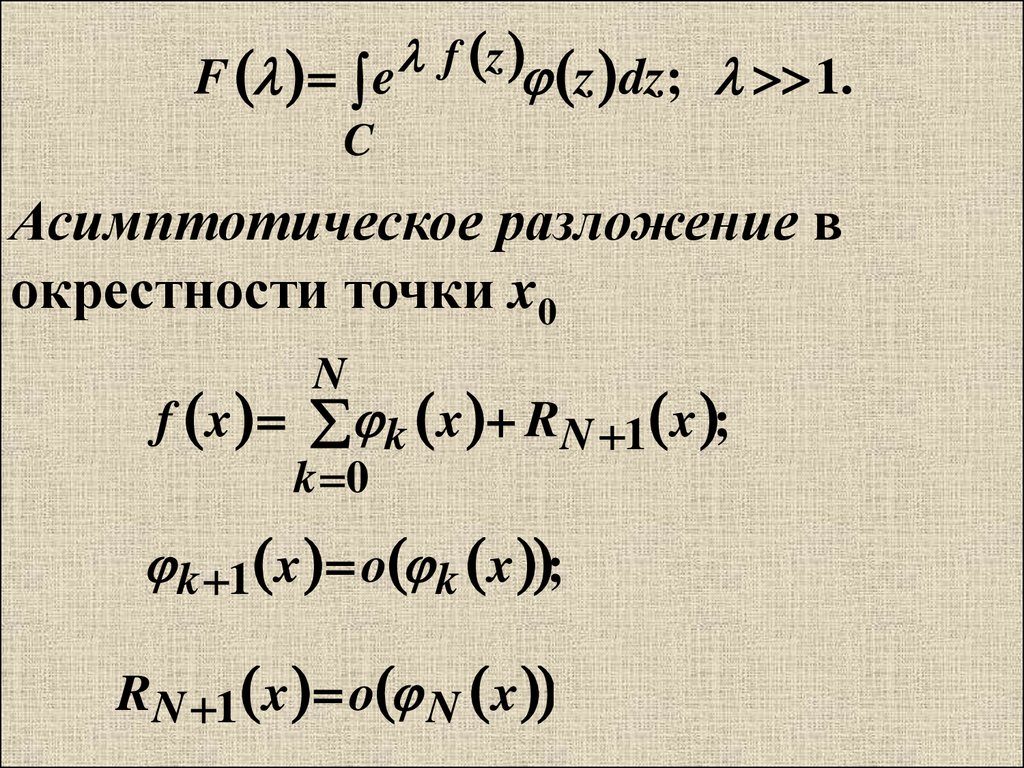












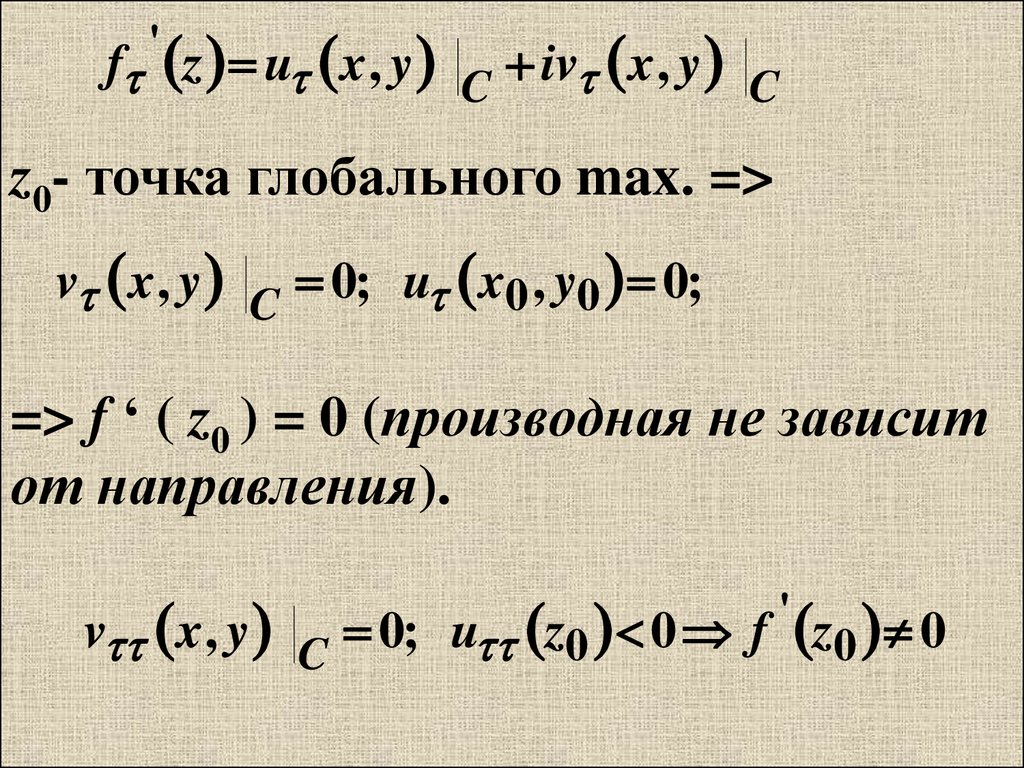







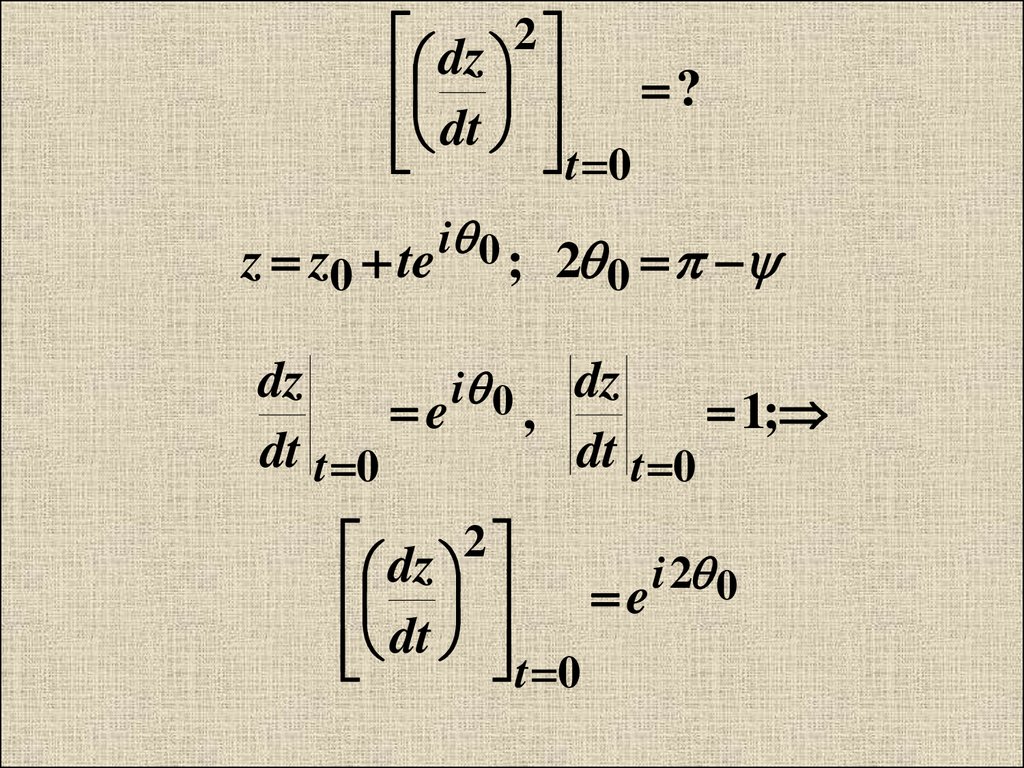

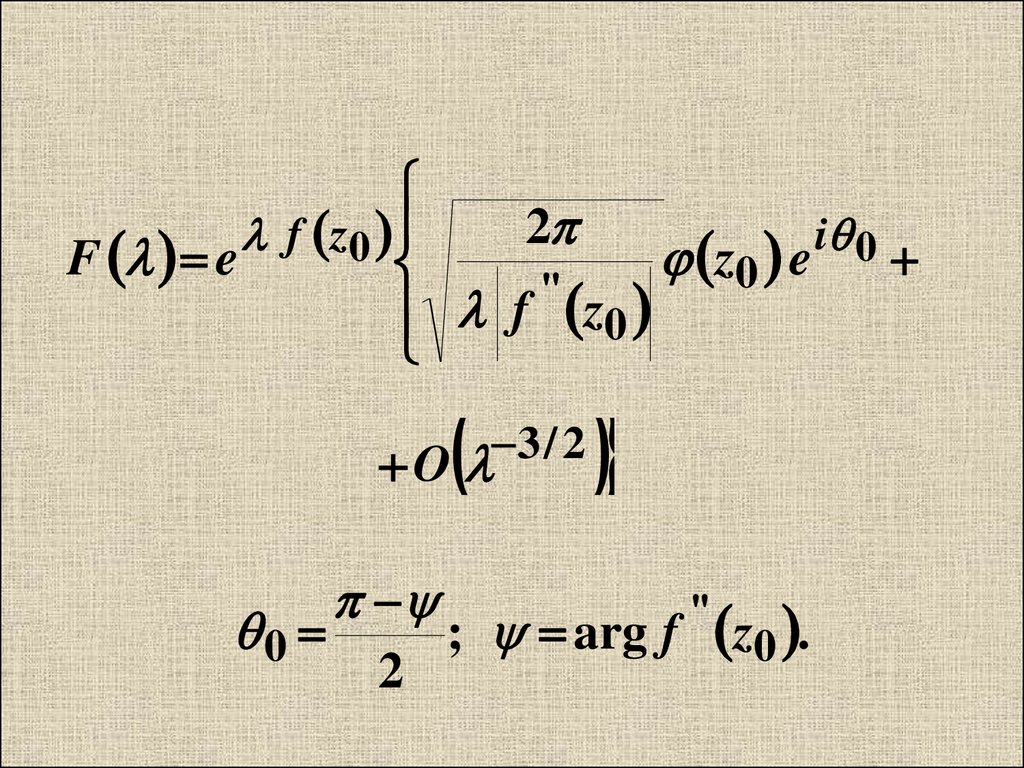

 Математика
Математика








