Похожие презентации:
Свойства аналитических ФКП. Лекция 5
1. Свойства аналитических ФКП
Утв. (о результатах арифметических операцийнад АФ).
f ( z), g ( z ) A D
f ( z) g ( z) A D
f ( z) g ( z) A D
f ( z)
A D , g ( z ) 0 z D
g ( z)
2.
Утв. (об аналитичности композиции АФ).Если w = f(z) A(D(z)), а в области ее значений
E(w) определена АФ g = (w), то функция
F(z) = (f(z)) A(D(z)).
П. Функция
F ( z) e
sin z
т.к.
A C( z) ,
w f ( z ) sin z A C ( z )
g ( w) e A C ( w) .
w
3.
Утв. (об аналитичности обратной функции).w f ( z ) A D( z ) f z 0 z D( z )
1
1
f (w) A E (w) f w
.
f
z
1
Утв. (о бесконечной дифференцируемости АФ).
Функция f(z), аналитическая в области D имеет в
каждой точке этой области производные любого
порядка:
f ( z ) A D( z ) f ( z ) C D( z ) .
4. Геометрический смысл производной ФКП
Пусть w = f(z) – аналитическая в точке z0 .f ( z0 ) k (cos i sin ) 0
w
lim z f ( z0 )
z 0
lim w f ( z )
0
z 0 z
w
lim arg
( z0 )
arg
f
z
z 0
5.
6.
ww
k f ( z0 ) lim
lim
z 0 z
z 0 z
- коэффициент локального растяжения (k>1) или
сжатия (k<1);
arg f ( z0 ) lim arg w lim arg z
z 0
z 0
lim lim ,
z 0
z 0
это угол, на который нужно повернуть
касательную в точке z0 к кривой , чтобы
получить угол, образованный касательной к
кривой Г в точке w0.
7. Понятие конформного отображения
Опр. Отображение окрестности точки z0 наокрестность точки w0, осуществляемое
функцией w = f(z) , называется конформным,
если в точке z0 оно обладает свойством
сохранения углов между линиями и
постоянством растяжений.
Опр. Отображение w = f(z) называется
конформным в области D, если оно
конформно в каждой точке этой области.
8.
Т. (критерий конформности).Для того чтобы отображение w = f(z) было
конформным в области D, необходимо и
достаточно, чтобы в этой области функция
w=f(z) была однолистной и аналитической,
причем
f ( z ) 0 z D.
Упр. Доказать, что отображение f(z) = ez
конформно в каждой точке z∈ C, однако не
является конформным во всей C.
9.
Лекция 5Интегрирование ФКП
10.
Пусть на комплексной плоскости задана криваяAB – ориентированная, незамкнутая, кусочногладкая, без самопересечений:
AB z C : z(t ) x(t ) iy(t ), t
Разобьем AB произвольным образом:
A z0 , z1 , z2
zn B
На каждом из участков выберем произвольные
точки
0 , 1 , , n 1
11.
12.
Пусть на дуге AB определена ФКП f(z). Найдемее значения в точках:
f ( 0 ), f ( 1 ), , f ( n 1 )
и составим интегральную сумму:
n 1
f ( k ) zk
k 0
Опр. Если существует
n 1
lim
max| zk | 0
f (
k 0
k
) zk ,
13.
не зависящий от способа разбиения дуги AB ивыбора точек k , то этот предел называют
интегралом ФКП по кривой AB и обозначают:
AB
f ( z )dz
n 1
lim
max| zk | 0
f (
k 0
k
) zk .
Т. (о существовании интеграла ФКП)
Пусть функция f(z) непрерывна на некоторой
кусочно-гладкой кривой L, тогда интеграл по
кривой L от этой функции существует, причем
14.
еслиf z u( x, y) iv x, y
то
f ( z )dz u iv d x iy
L
L
udx vdy i udy vdx;
L
если
L
L z(t ), t ,
L
то
f z dz f z t z t dt.
14
15.
Свойства интеграла от ФКП1.
f ( z)dz f ( z)dz
L
2.
L
Af ( z ) Bg ( z) dz A f ( z )dz B g ( z )dz
L
3.
L
L1 L2
4.
L
f ( z )dz f ( z )dz f ( z )dz
L1
f ( z )dz
L2
M l , где f ( z ) M ;
L
l length( L).
z L
16.
П. Вычислитьz z dz ,
L
где L – часть окружности
L z 1, 0 arg z
16
17.
Параметризация:L z e , 0 t
it
z z dz
z e
it
dz ie dt
it
L
e ie dt i dt i.
0
it
it
0
17
18.
П. Вычислитьz
L
2
zz dz ,
где L – дуга параболы L y x 2 , 0 x 1 .
18
19.
Выделим действительную и мнимую частиподынтегральной функции:
z zz x iy x iy x iy
2
2
2 x i 2 xy.
2
z
2
zz dz u iv d x iy
L
L
2 x i 2 xy d x iy
2
L
y x ,
2
0 x 1
1
2 x i 2 xx d x ix
2
0
2
2
19
20.
11
2 x 4 x dx i 4 x 2 x dx
2
4
3
0
3
0
1
1
2 3
2 x 2 x dx 6i x dx i.
15 2
0
0
2
4
3
20













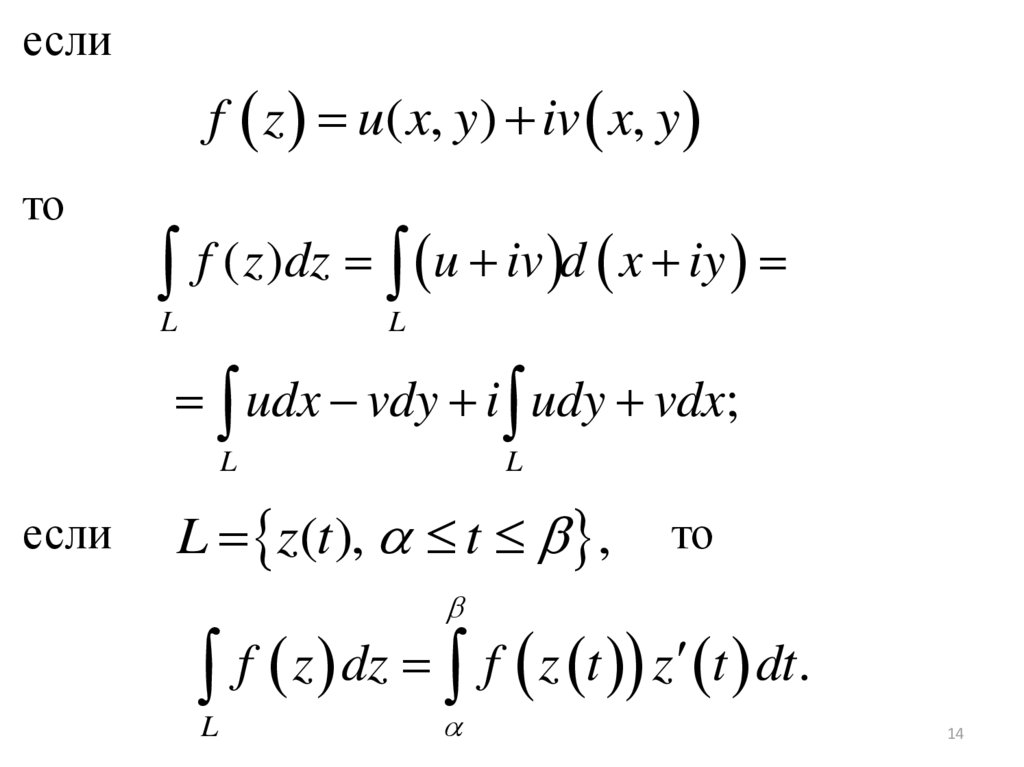





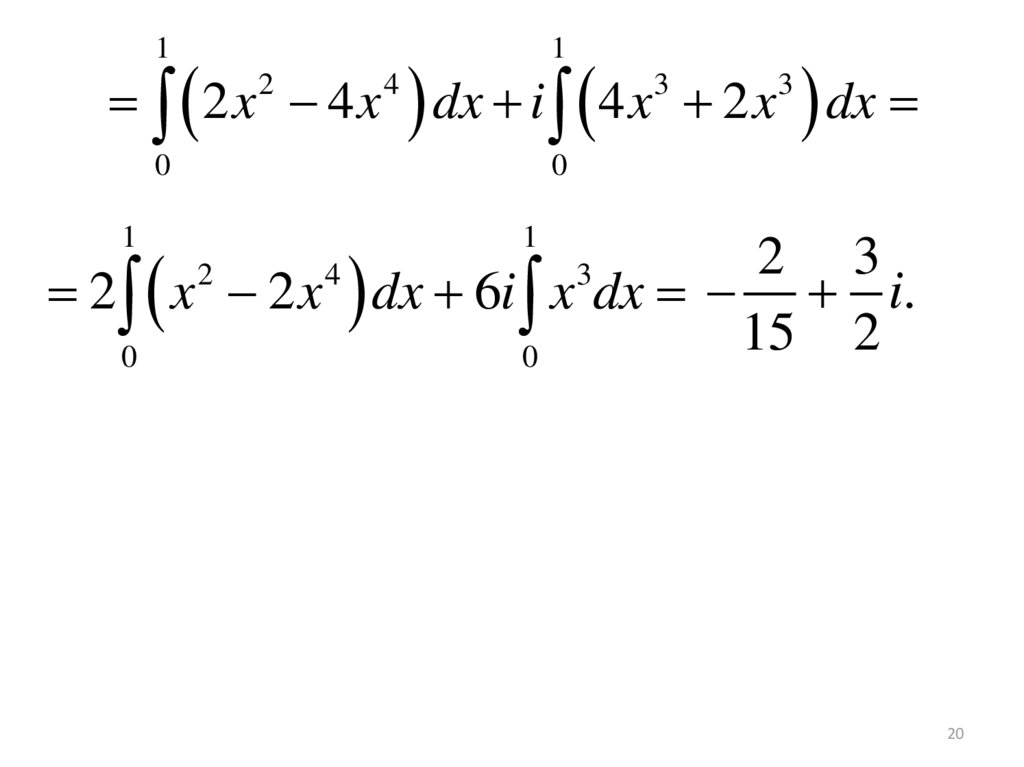
 Математика
Математика








