Похожие презентации:
Интегрирование ФКП
1.
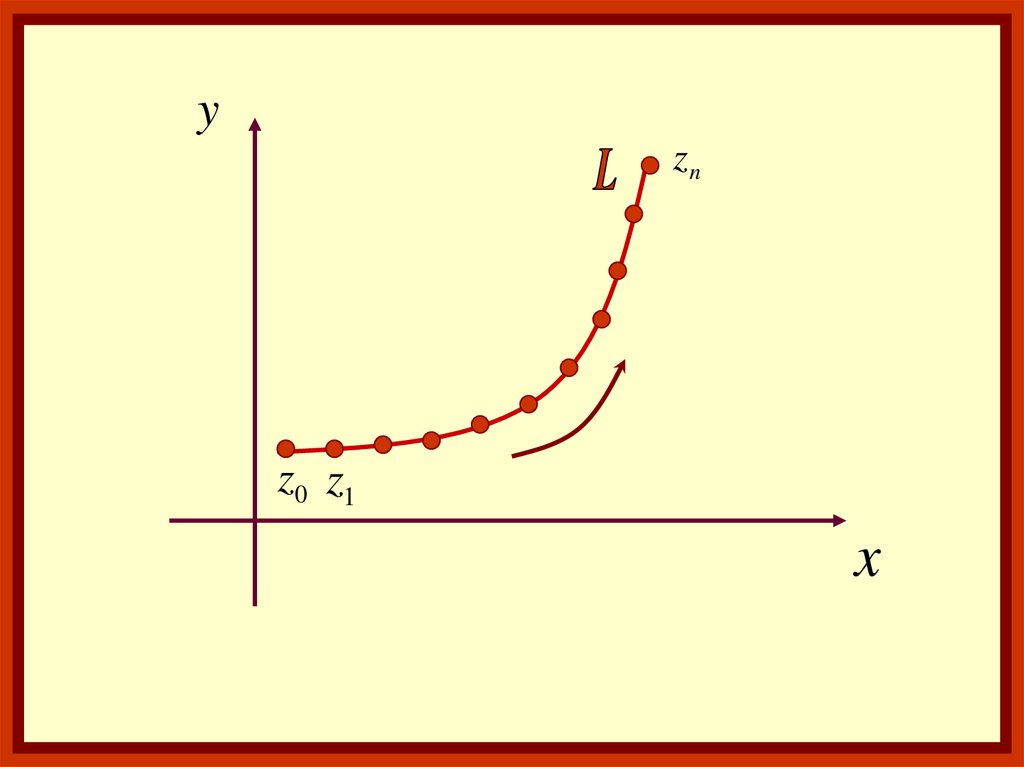
Пусть на комплексной плоскости z дана криваяL. Граничные точки этой кривой: z0 и zn (если
кривая замкнутая, то z0=zn).
Установим положительное направление: от точки
z0 к zn.
Предположим, что функция комплексного
аргумента z непрерывна во всех точках этой
кривой.
Разобьем кривую точками на элементарные дуги.
2.
yzn
z0 z1
x
3.
Обозначимz1 z0 z1
z2 z1 z2 ... zn zn 1 zn
где число Δzi изображается вектором, идущим из
точки zi-1 в точку zi.
zi
-длина
этого
вектора,
т.е.
хорда,
стягивающая
соответствующую
элементарную дугу.
Внутри каждой элементарной дуги выбираем
произвольную точку ξi.
n
Составим сумму
f ( ) z
i 1
i
i
4.
Данная сумма будет интегральной.Предел этой суммы при стремлении к нулю длин
всех дуг будет интегралом функции f(z) по
кривой L:
n
lim
zi 0
f ( ) z f ( z)dz
i 1
i
i
L
5.
1Интеграл от суммы (разности) двух или
нескольких функций равен сумме (разности)
интегралов от этих функций:
f ( z) f
1
L
2
( z ) dz f1 ( z )dz f 2 ( z )dz
L
L
6.
2Постоянную величину можно выносить
за знак интеграла:
C
f
(
z
)
dz
C
f
(
z
)
dz
L
L
7.
3Если кривая L геометрически совпадает с
кривой L1, но имеет противоположное
направление, то:
f ( z )dz f ( z )dz
L
L1
8.
4Если кривая разбита на дуги L1 L2 …Ln то:
f ( z)dz f ( z)dz f ( z )dz ... f ( z)dz
L
L1
L2
Ln
9.
Вычислениеинтеграла
ФКП
сводится
вычислению криволинейного интеграла
функции действительного переменного.
Пусть
z x i y
f ( z) u i v
u u ( x, y )
v v ( x, y )
Обозначим
zi xi i yi
(i 1,2,..., n)
i i i i
(i 1,2,..., n)
к
от
10.
Тогдаzi ( xi 1 i yi 1 ) ( xi i yi )
( xi 1 xi ) i ( yi 1 yi ) xi i yi
xi
yi
Поскольку
f ( i ) u( i , i ) i v( i , i )
11.
f ( i ) zi u( i , i ) i v( i , i ) ( xi i yi )u ( i , i ) xi v( i , i ) yi
i (u ( i , i ) yi v( i , i ) xi )
Переходим к пределу
n
f ( z)dz lim u( , ) x v( , ) y
L
z i 0
i 1
i
i
i
i
i
i (u ( i , i ) yi v( i , i ) xi )
i
12.
f ( z )dz u ( x, y )dx v( x, y )dyL
L
i u ( x, y )dy v( x, y )dx
L
13.
Эта формула показывает, чточтобы свести
интеграл по комплексному аргументу к
вычислению
обычного
криволинейного
интеграла, нужно выделить в подынтегральной
функции действительные и мнимые части
f ( z) u i v
и умножить ее на
dz dx i dy
Если кривая L задана параметрически
x x (t )
y y (t )
14.
иначальная и конечная
соответственно t0 и tn
точки
кривой
то исходный интеграл сводится к определенному:
tn
f ( z)dz f ( z(t )) z (t )dt
L
t0
15.
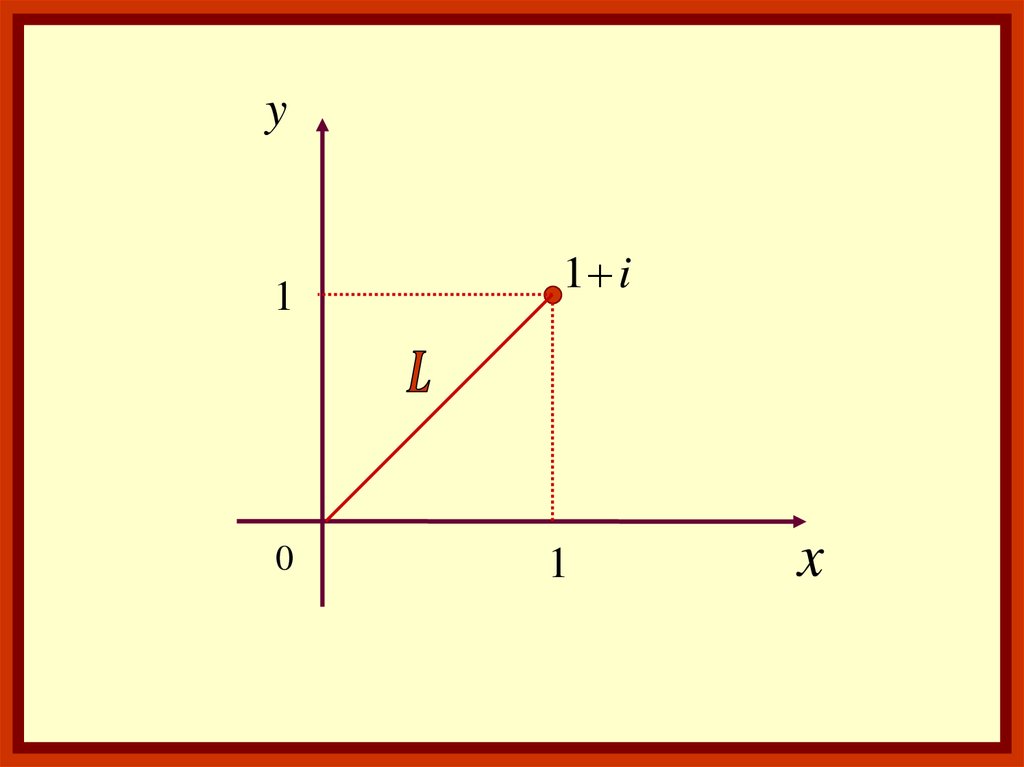
Вычислить интеграл:Re( z)dz
L
Где L – отрезок, соединяющий
точки 0 и 1+i
16.
y1
0
1 i
1
x
17.
Запишем уравнение отрезка в параметрическомвиде:
x t
y t
или
z (1 i ) t
0 t 1
dz (1 i ) dt
Тогда
18.
1Re(
z
)
dz
Re
(
1
i
)
t
(
1
i
)
dt
L
0
2 1
t
1 i
(1 i ) tdt (1 i )
20
2
0
1















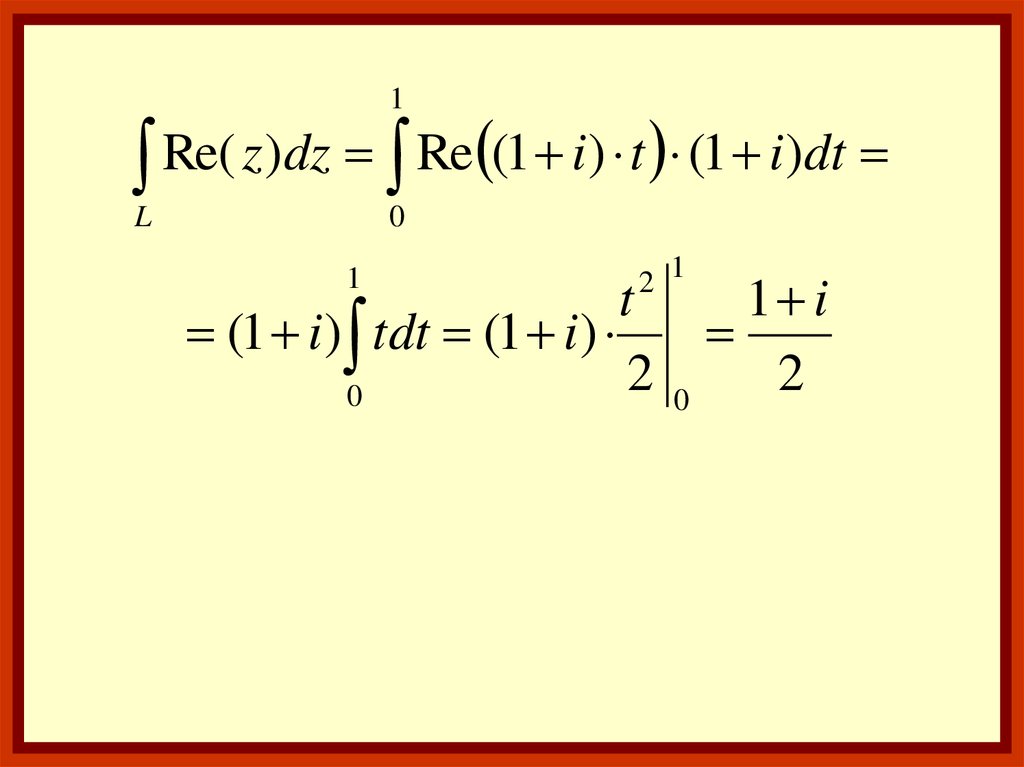
 Математика
Математика








