Соотношения между сторонами и углами треугольника

1.

2.

B
BC
BC
AC
sin
tgAA
cos
AC
AB
AB
С
А
Тангенсом
Синусом
Косинусом
острого
острого
острогоугла
угла
угла прямоугольного
прямоугольного
прямоугольного
треугольника
треугольника
треугольника называется
называется отношение
отношение
отношение
противолежащего
противолежащего
прилежащего катета
катета
катета
к гипотенузе
ккприлежащему
гипотенузе

3.

BC
sin A
AB
AC
cos A
AB
BC
tgA
AC
В
С
sin A
tgA
;
cos A
А
sin B
tgB
cos B
AC
sin B
AB
BC
cos B
AB
AC
tgB
BC

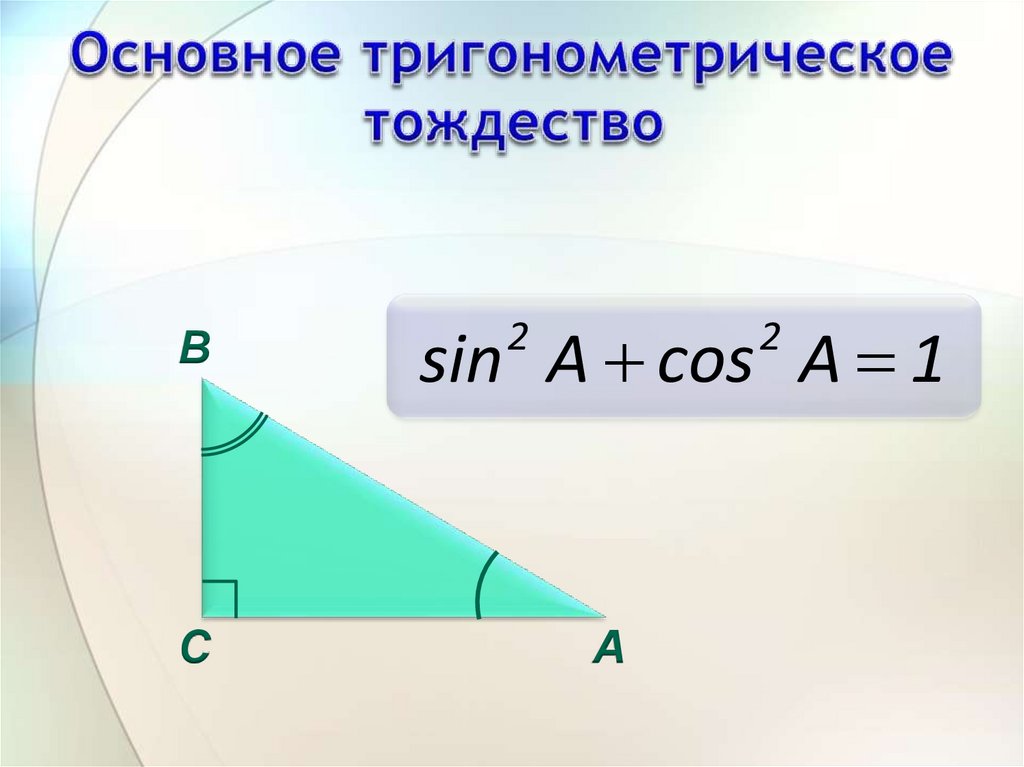
4.

В
С
sin А cos А 1
2
2
А

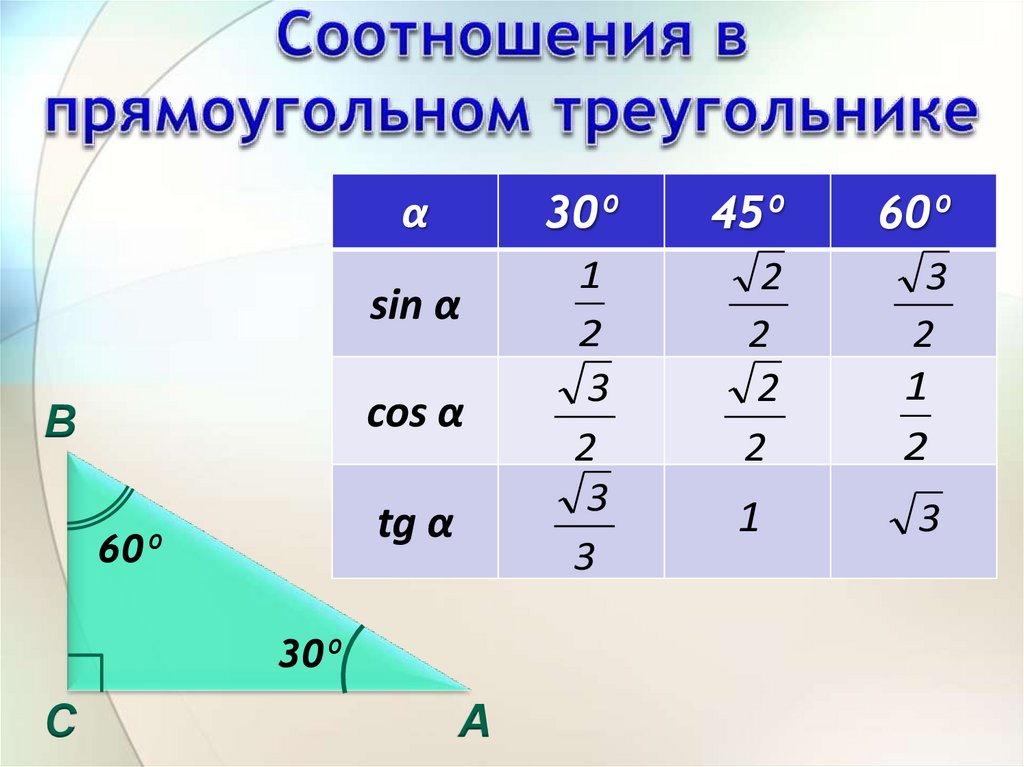
5.

α
sin α
cos α
В
tg α
60º
30º
С
А
30º
45º
60º
1
2
3
2
3
3
2
2
2
2
3
2
1
2
1
3

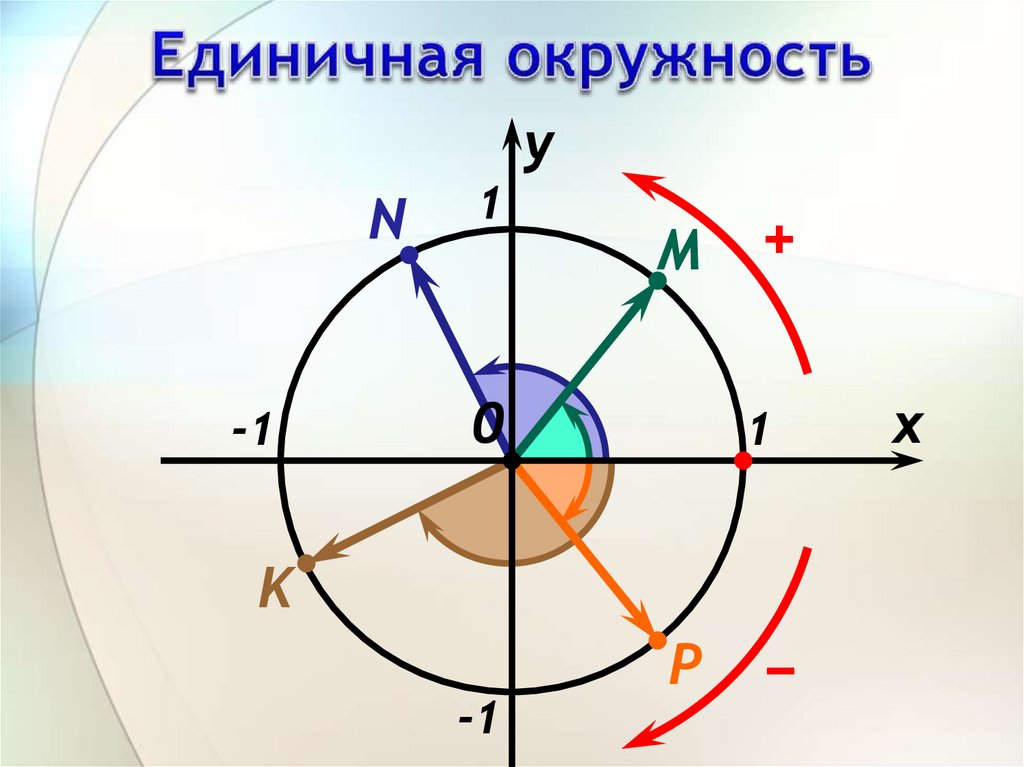
6.

y
N
-1
1
M
0
+
1
K
−
-1
P
x

7.

Синус угла α –
это число, равное
ординате точки
единичной
окружности,
соответствующей
углу α (sin α)
Косинус угла α –
это число, равное
абсциссе точки
единичной
окружности,
соответствующей
углу α (cos α)
y
1
M
sin α
α
-1
0
-1
cos α
1
x

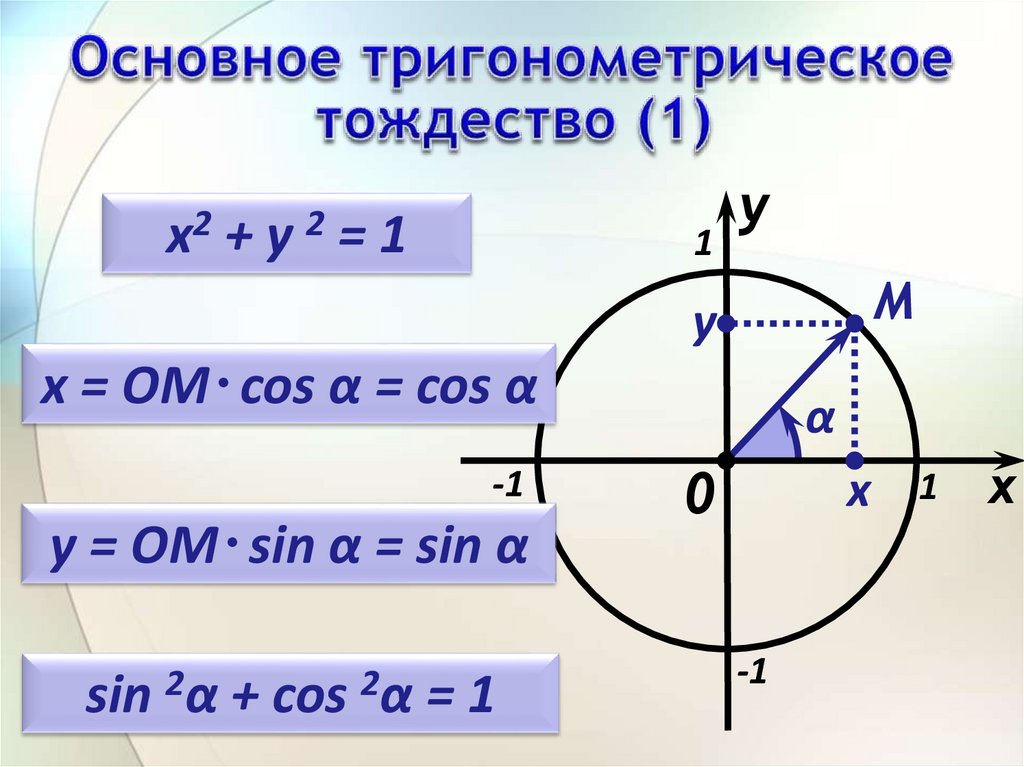
8.

x2 + y 2 = 1
1
x = ОM ∙ cos α = cos α
-1
y = ОM ∙ sin α = sin α
sin 2α + cos 2α = 1
y
M
y
α
0
x
-1
1
x

9.

sin (90° – α) = cos α
cos (90° – α) = sin α
sin (180° – α) = sin α
cos (180° – α) = – cos α

10.

11.

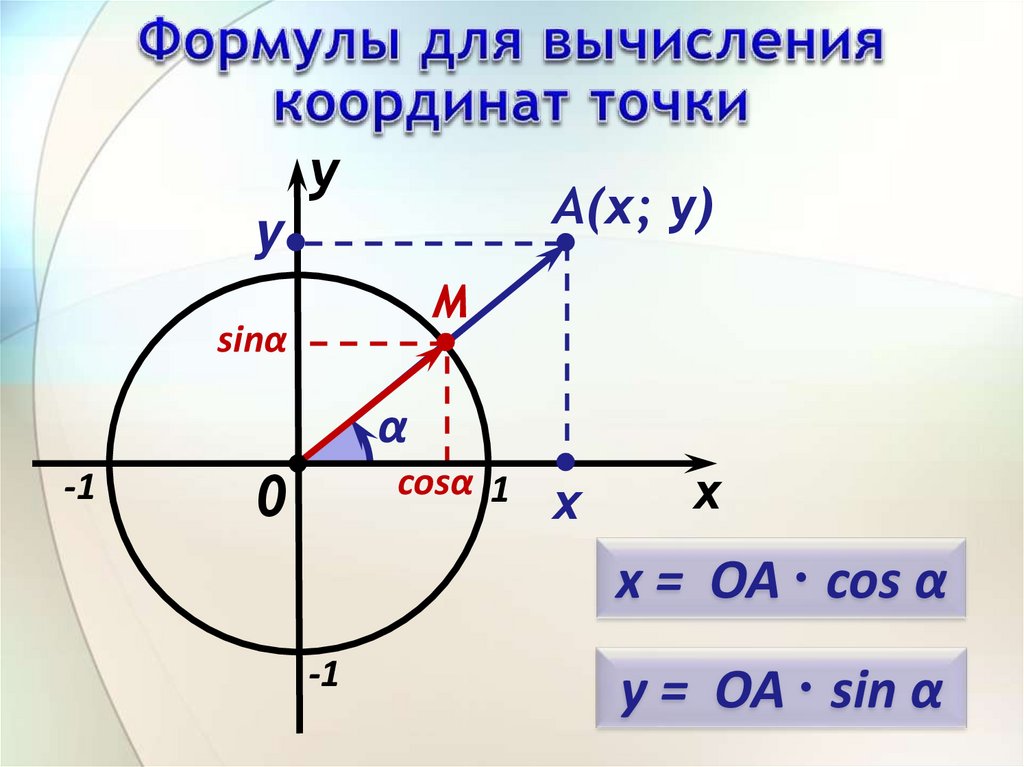
y
А(х; у)
y
M
sinα
α
-1
0
cosα 1
х
x
x = ОА ∙ cos α
-1
y = ОА ∙ sin α

12.

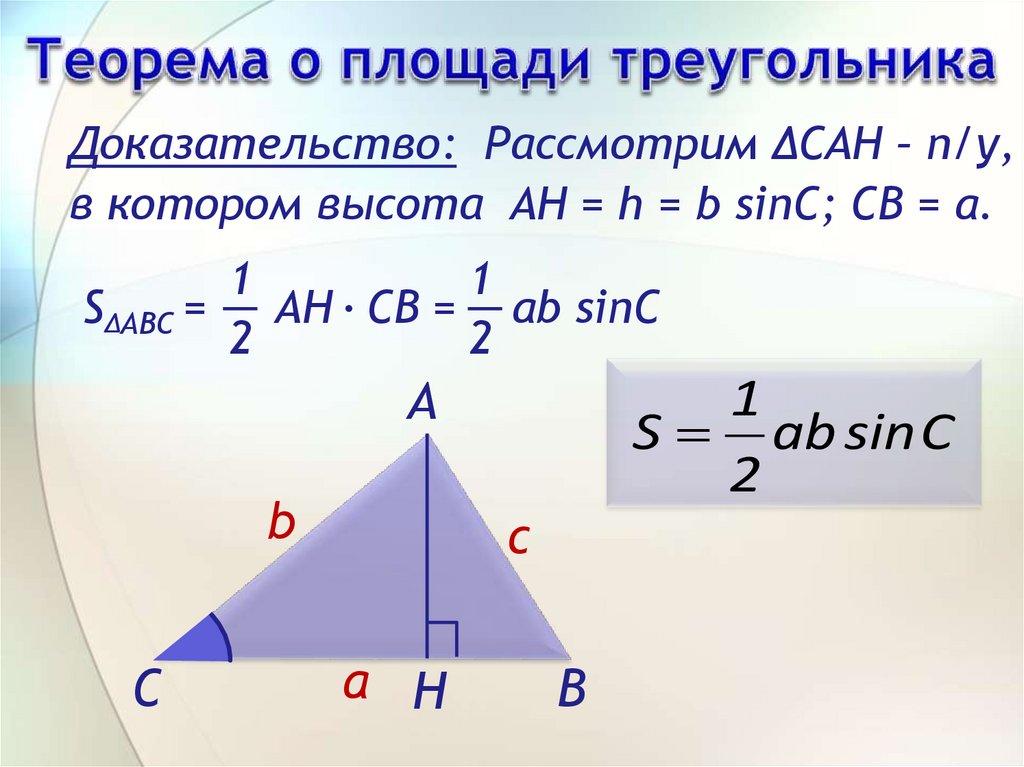
Площадь треугольника равна половине
произведения двух его сторон на синус
угла между ними
1
S ab sin C
2
А
b
С
c
a H
В
Дано: ∆АВС
Доказать:
S∆ABC = 1 ab sin C
2

13.

Доказательство: Рассмотрим ∆САН – п/у,
в котором высота AH = h = b sinC; CB = a.
1
1
S∆ABC = AH ∙ CB = ab sinC
2
2
А
b
С
1
S ab sin C
2
c
a H
В

14.

Домашнее задание
• В веб