Использование метода целесообразно подобранных задач при обучении школьников решению тригонометрических уравнений и неравенств

1.

ИСПОЛЬЗОВАНИЕ МЕТОДА
ЦЕЛЕСООБРАЗНО ПОДОБРАННЫХ
ЗАДАЧ ПРИ ОБУЧЕНИИ
ШКОЛЬНИКОВ РЕШЕНИЮ
ТРИГОНОМЕТРИЧЕСКИХ
УРАВНЕНИЙ И НЕРАВЕНСТВ
студентки 3 курса заочной формы обучения
Лузгачевой Ольги Владимировны
Научный руководитель
к.п.н., доцент кафедры физики и математики
Алмазова Т.А.

2.

Цель исследования заключается в разработке
методики применения целесообразно
подобранных задач для построения ИОТ
учащихся в процессе обучения учащихся
решению тригонометрических уравнений и
неравенств.
Объект исследования - процесс изучения
тригонометрического материала в курсе
алгебры и начал анализа.
Предмет исследования – метод целесообразно
подобранных задач и дидактические
возможности его использования при обучении
учащихся решению тригонометрических
уравнений и неравенств.

3.

Гипотеза исследования: Метод целесообразно
подобранных задач способствует
качественному обучению решать
тригонометрические уравнения и неравенства
при изучении курса алгебры и начал анализа
и служит основой для построения
индивидуальных образовательных траекторий
учащихся.

4.

ДЛЯ ДОСТИЖЕНИЯ ПОСТАВЛЕННОЙ ЦЕЛИ И ПРОВЕРКИ
СФОРМУЛИРОВАННОЙ ГИПОТЕЗЫ НЕОБХОДИМО БЫЛО
РЕШИТЬ СЛЕДУЮЩИЕ ЧАСТНЫЕ ЗАДАЧИ
Задачи исследования:
выявить роль тригонометрических уравнений и
неравенств в обучении математики;
классифицировать методы и приемы решения
тригонометрических уравнений и неравенств;
разработать блоки задач к урокам-практикумам по
темам «Решение простейших тригонометрических
уравнений», «Решение тригонометрических
неравенств», «Решение тригонометрических
уравнений методом разложения на множители»;
раскрыть методику изучения тригонометрических
уравнений и неравенств в курсе математики
старшей школы с использованием метода
целесообразно подобранных задач и проверить ее
эффективность в ходе педагогического
эксперимента.

5.

РОЛЬ И МЕСТО ТРИГОНОМЕТРИЧЕСКОГО
МАТЕРИАЛА
Изучению темы «Решение тригонометрических
уравнений» часто предшествует изучение таких
тем как «Преобразование тригонометрических
выражений» и «Основные свойства и графики
тригонометрических функций».
В разделе «Решение тригонометрических
уравнений и неравенств» учащиеся знакомятся с
понятиями арксинус, арккосинус, арктангенс.
Осознание важности изучаемого материала
приходит к ученикам не в процессе его изучения, а
в процессе его применения при решении других
заданий, т.е. тогда когда он становится средством
для решения других задач.

6.

КЛАССИФИКАЦИЯ МЕТОДОВ РЕШЕНИЯ
ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ:
1)Аналитические методы:
-Простейшие тригонометрические уравнения и сводящиеся к ним;
-Тригонометрические уравнения, решаемые методом замены переменной:
а) сводящиеся к квадратным уравнениям;
б)сводящиеся к уравнениям высших степеней(кубическому,биквадратному и т.д);
в) сводящиеся к дробно-рациональным уравнениям;
-Тригонометрические уравнения, решаемые методом разложения на множители с
использованием известных методов(вынесение общего множителя за скобки,
использование формул сокращенного умножения, группировка) или с
предварительным использованием тригонометрических формул(двойного аргумента,
формул сложения и т.д);
- Сведедение уравнений к известному виду (однородные 1 или 2 степени,
симметрические, линейные относительно или );
-Использование искусственных приемов(универсальная тригонометрическая
подстановка, использование равенства одноименных тригонометрических функций,
использование приема введения вспомогательного угла и т.д).
2)Графические методы:
-Оценка выражений, входящих в уравнение;
-Использование монотонности и ограниченности функций;
-Использование графиков функций.

7.

РАССМОТРИМ СОДЕРЖАНИЕ МАТЕРИАЛА ПО ТРИГОНОМЕТРИИ,
ИЗЛОЖЕННОГО В РАЗЛИЧНЫХ УЧЕБНИКАХ ПО МАТЕМАТИКЕ
ЗА КУРС 10 – 11 КЛАСС СРЕДНЕЙ ШКОЛЫ:
- А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын,
Б.М. Ивлев, С.И. Шварцбурд “Алгебра и
начала анализа 10–11 класс”;
-С.М. Никольский, М.К. Потапов, Н.Н.
Решетников, А.В. Шевкин “Алгебра и
начала анализа 10 класс”;
-Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров, Н.Е.
Федорова, М.И. Шабунин “Алгебра и начала
анализа 10–11 класс”;
-Ю.М. Колягин, Ю.В. Сидоров, М.Ю. Ткачева, Н.Е.
Федорова, М.И. Шабунин “Алгебра и
начала анализа 10 класс”;
-М.И. Башмаков “Алгебра начала анализа 10–11
класс”;
-А.Г. Мордкович Алгебра и начала анализа ч.1
учебник.

8.

МЕТОД ЦЕЛЕСООБРАЗНО ПОДОБРАННЫХ ЗАДАЧ
РЕАЛИЗУЕТ СЛЕДУЮЩИЕ ДИДАКТИЧЕСКИЕ ЦЕЛИ:
Вовлечение школьников в самостоятельную
поисковую познавательную деятельность;
формирование их познавательных
способностей, навыков оценки своих
возможностей и уровня подготовки, навыков
самоорганизации;
навыков построения индивидуальной
образовательной траектории(ИОТ) при
изучении различных тем школьного курса
математики.

9.

ИНДИВИДУАЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ
ТРАЕКТОРИЯ(ИОТ)
В самом широком смысле индивидуальная
образовательная траектория (ИОТ) – это
персональный путь реализации личностного
потенциала ученика в образовании.
Основные элементы
индивидуальной образовательной деятельности
ученика - это смысл деятельности (зачем личной
цели (предполагаемый результат);
план деятельности; реализация плана;
рефлексия (осознание собственной
деятельности); оценка; корректировка или переоп
ределение целей.
Условием достижения целей и задач личностноориентированного обучения является сохранение
индивидуальных особенностей учеников, их
уникальности, разноуровневости
и разноплановости.

10.

МЕТОДИКА ИСПОЛЬЗОВАНИЯ ЦЕЛЕСООБРАЗНО
ПОДОБРАННЫХ ЗАДАЧ ДЛЯ ПОСТРОЕНИЯ ИНДИВИДУАЛЬНОЙ
ОБРАЗОВАТЕЛЬНОЙ ТРАЕКТОРИИ
1)Учитель заранее формирует дифференцированный
набор задач к этому уроку.
2)Учителем осуществляется наполнение каждого из
определенных на предыдущем шаге блоков задач. Блоки
наполняются задачами таким образом, что каждый из
них содержит необходимое и достаточное количество
задач данного уровня сложности, для формирования
навыков решения задач по теме.
3)Учителем разрабатывается инструкция, в которой
описывается как ученик должен осуществить работу с
предложенной ему на уроке системой задач (блоками
задач) для того, чтобы выстроить индивидуальную
образовательную траекторию формирования умений и
навыков решения задач по изучаемой теме.
4)Учитель определяет, какое минимальное количество
задач из каждого обязательного блока должен
выполнить каждый учащийся, чтобы перейти к
следующему блоку.

11.

БЛОК №5 «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ,
СВОДЯЩИЕСЯ К ПРОСТЕЙШИМ, СОДЕРЖАЩИЕ
ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ».
В этот блок входят уравнения, содержащие
«сложный» аргумент у одной из
тригонометрических функций (синус, косинус,
тангенс или котангенс), или наряду со
«сложным» аргументом требуется выполнить
ряд несложных преобразований, чтобы
выразить тригонометрическую функция,
однако требование задачи содержит условие,
что корни уравнения должны удовлетворять
какому-либо свойству. Например, они могут
принадлежать какому-либо промежутку или
требуется найти наименьший положительный
корень или наибольший отрицательный и т.д.

12.

БЛОК №5 (ВСЕГО 7 ЗАДАЧ, МИНИМАЛЬНОЕ КОЛИЧЕСТВО ДЛЯ
ВЫПОЛНЕНИЯ 4 ЗАДАЧИ)
ВЫПОЛНИТЕ СЛЕДУЮЩИЕ ЗАДАНИЯ.

13.

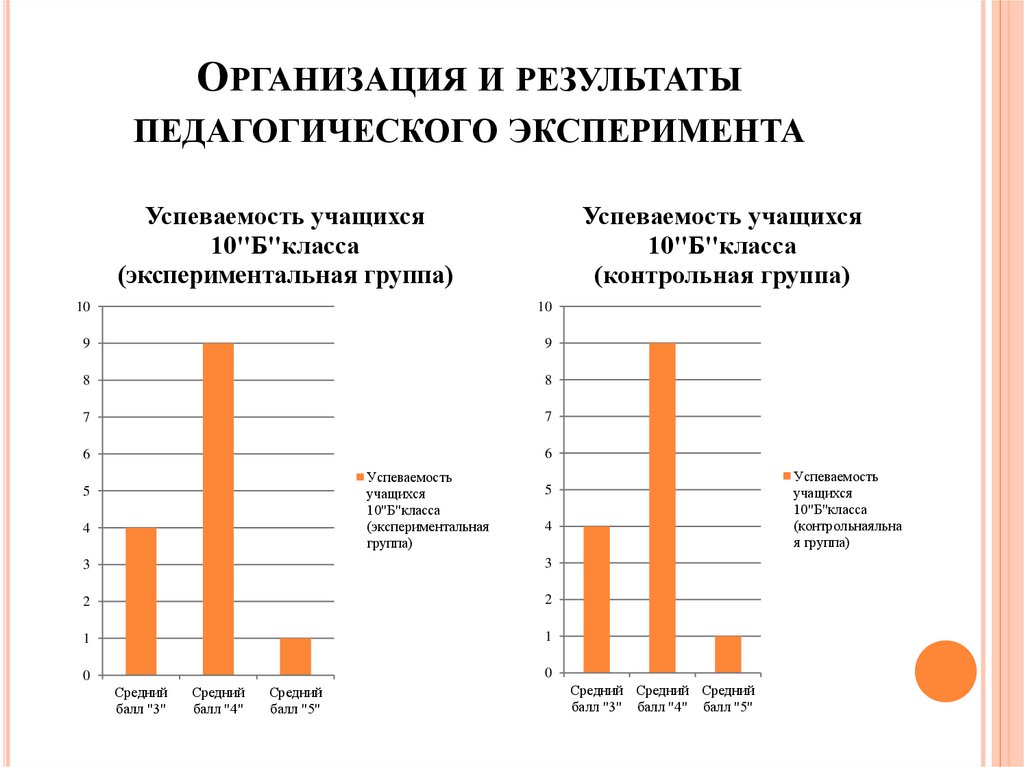
ОРГАНИЗАЦИЯ И РЕЗУЛЬТАТЫ
ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА
Успеваемость учащихся
10"Б"класса
(экспериментальная группа)
Успеваемость учащихся
10"Б"класса
(контрольная группа)
10
10
9
9
8
8
7
7
6
6
Успеваемость
учащихся
10"Б"класса
(экспериментальная
группа)
5
4
4
3
3
2
2
1
1
0
0
Средний
балл "3"
Средний
балл "4"
Средний
балл "5"
Успеваемость
учащихся
10"Б"класса
(контрольнаяльна
я группа)
5
Средний Средний Средний
балл "3" балл "4" балл "5"

14.

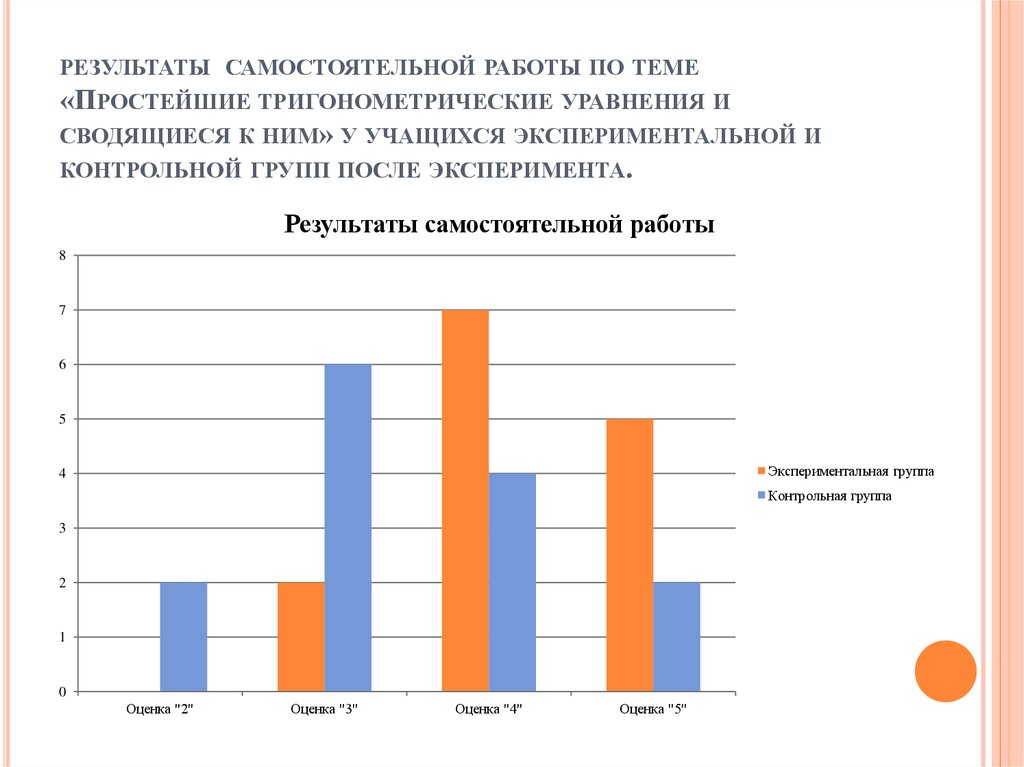
РЕЗУЛЬТАТЫ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО ТЕМЕ
«ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И
СВОДЯЩИЕСЯ К НИМ» У УЧАЩИХСЯ ЭКСПЕРИМЕНТАЛЬНОЙ И
КОНТРОЛЬНОЙ ГРУПП ПОСЛЕ ЭКСПЕРИМЕНТА.
Результаты самостоятельной работы
8
7
6
5
Экспериментальная группа
4
Контрольная группа
3
2
1
0
Оценка "2"
Оценка "3"
Оценка "4"
Оценка "5"

15.

ГИПОТЕЗЫ
Основная гипотеза Н0:
Статистически значимых различий в усвоении изученной темы с
помощью традиционной методики и методики выстраивания
индивидуальной образовательной траектории с
использованием метода целесообразно подобранных задач не
обнаружено.
Альтернативная гипотеза Н1:
Обнаружены статистически значимые различия в усвоении
изученной темы с помощью традиционной методики и
методики выстраивания индивидуальной образовательной
траектории с использованием метода целесообразно
подобранных задач.
Uemp=51.
Ukp(0.05)=55;
Ukp(0.01)=42.
Эмпирическое значение критерия попадает в область между
U0,05 и U0,01. Гипотеза H1 принята на уровне значимости не
менее 95%.

16.

Спасибо за внимание!