Похожие презентации:
Соотношение между сторонами и углами в прямоугольном треугольнике. Урок для 8 класса
1. Соотношение между сторонами и углами в прямоугольном треугольнике
урок для 8 класса2.
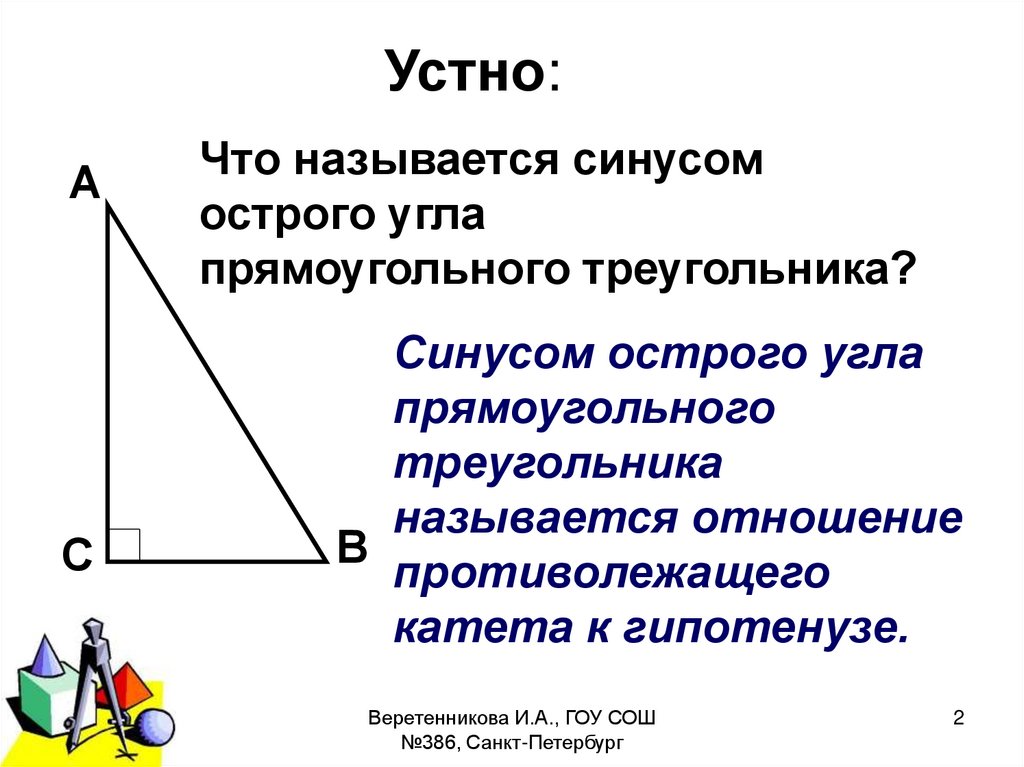
Устно:А
С
2011 г.
Что называется синусом
острого угла
прямоугольного треугольника?
Синусом острого угла
прямоугольного
треугольника
называется отношение
В
противолежащего
катета к гипотенузе.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
2
3.
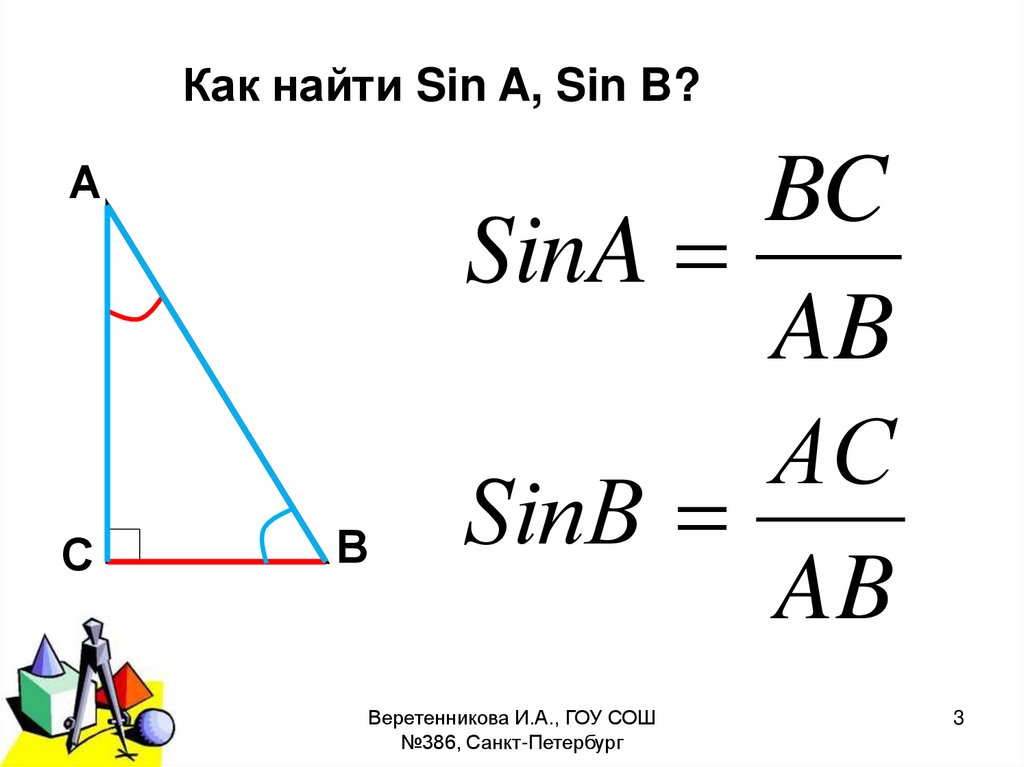
Как найти Sin A, Sin B?А
С
2011 г.
В
BC
SinA
AB
АC
SinВ
AB
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
3
4.
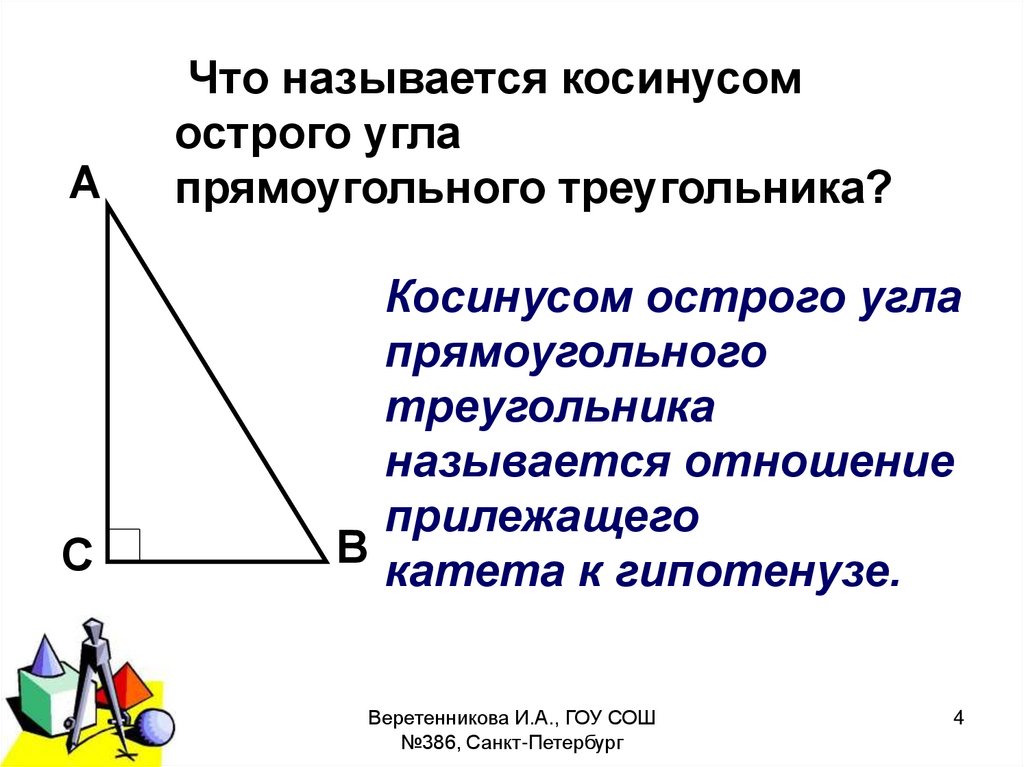
АС
2011 г.
Что называется косинусом
острого угла
прямоугольного треугольника?
Косинусом острого угла
прямоугольного
треугольника
называется отношение
прилежащего
В
катета к гипотенузе.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
4
5.
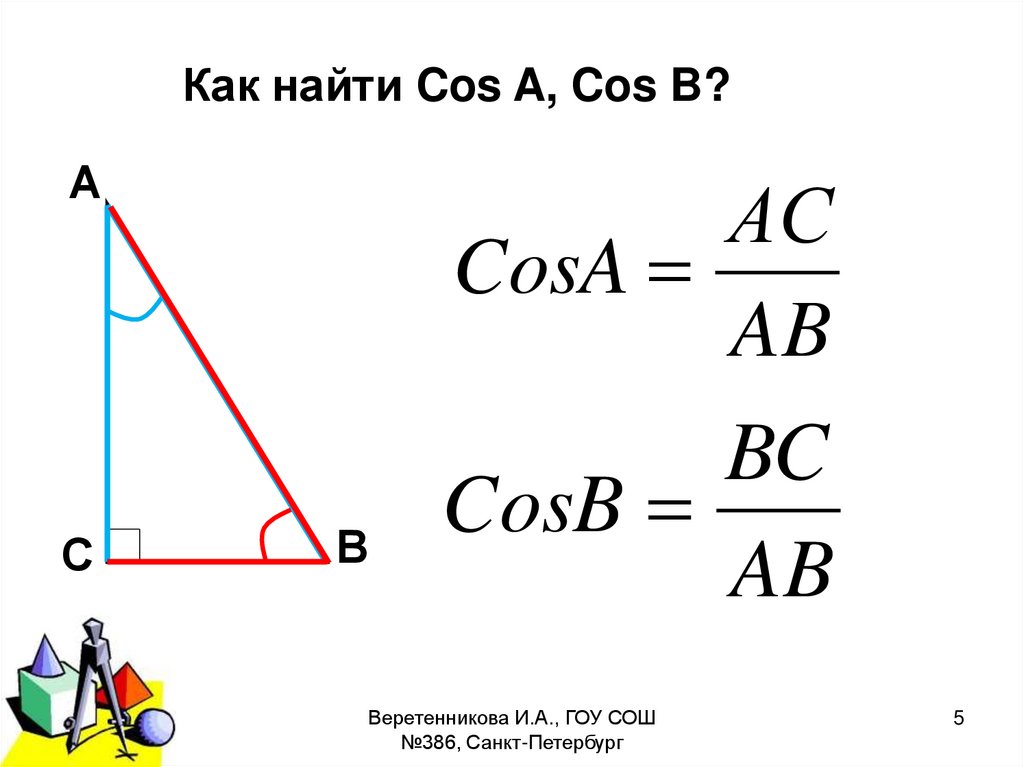
Как найти Cos A, Cos B?А
С
2011 г.
АC
CosA
AB
В
BC
CosB
AB
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
5
6.
Что можно сказать о Sin и Cosуглов одного прямоугольного
треугольника?
SinA CosB
CosA SinB
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
6
7.
АС
2011 г.
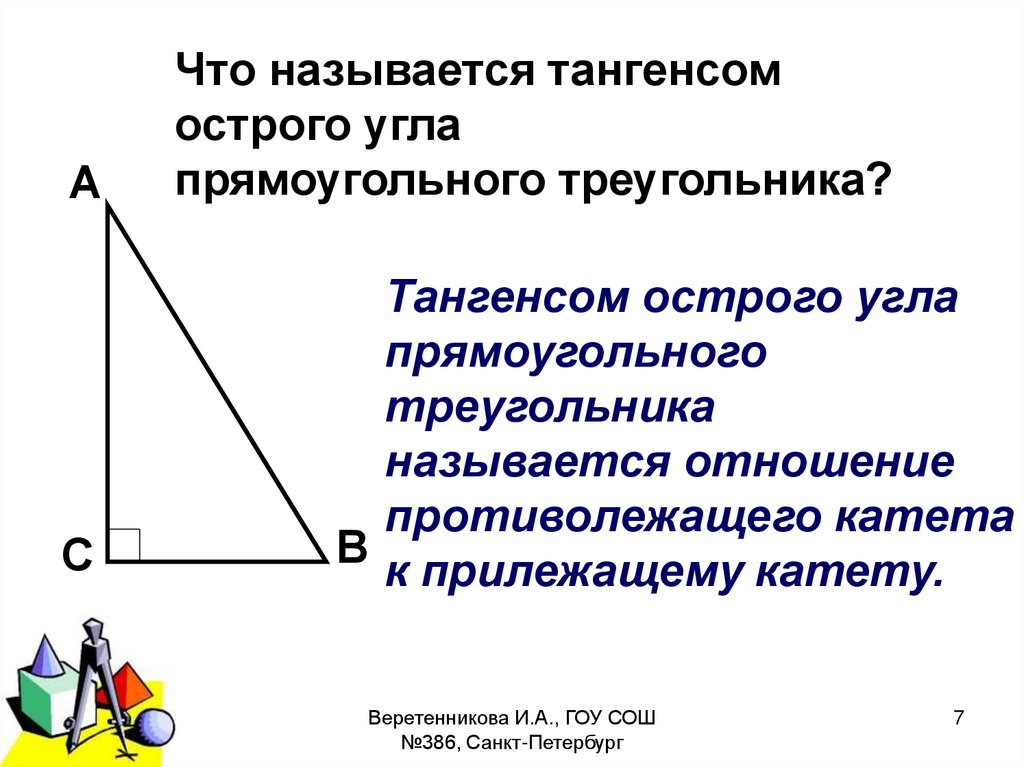
Что называется тангенсом
острого угла
прямоугольного треугольника?
Тангенсом острого угла
прямоугольного
треугольника
называется отношение
противолежащего катета
В
к прилежащему катету.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
7
8.
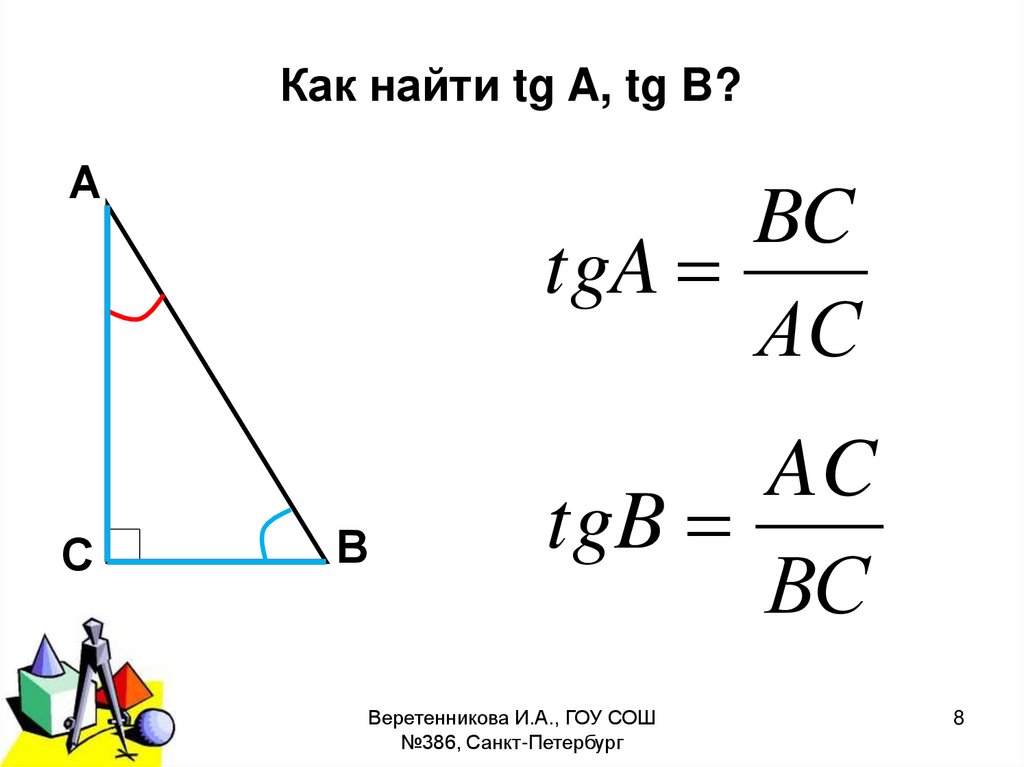
Как найти tg A, tg B?А
С
2011 г.
BC
tgA
AС
В
AC
tgB
BС
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
8
9.
Что вы знаете о Sin, Cos, tg равныхострых углов прямоугольных
треугольников?
Если острый угол одного
прямоугольного треугольника равен
острому углу другого прямоугольного
треугольника, то синусы этих углов
равны, косинусы этих углов равны
и тангенсы этих углов равны .
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
9
10.
Назовите формулуосновного тригонометрического
тождества.
Sin Cos 1
2
2
Сформулируйте теорему Пифагора.
Квадрат гипотенузы равен сумме
квадратов катетов.
a b c
2
2011 г.
2
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
2
10
11.
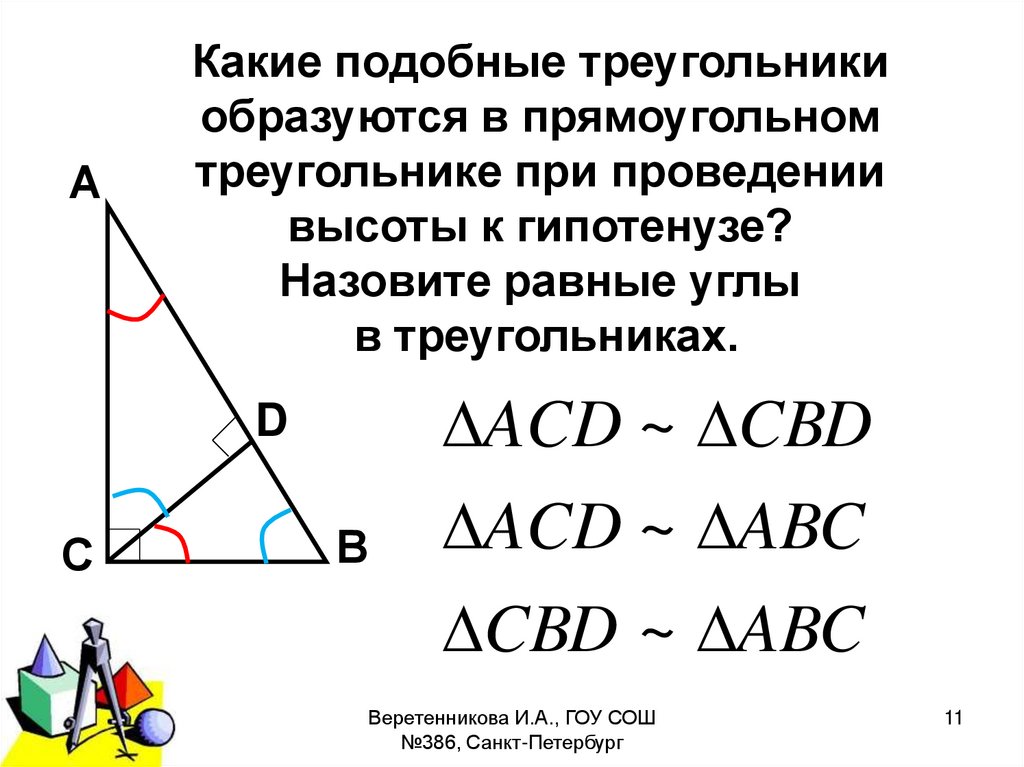
АКакие подобные треугольники
образуются в прямоугольном
треугольнике при проведении
высоты к гипотенузе?
Назовите равные углы
в треугольниках.
D
С
2011 г.
В
ACD ~ CBD
ACD ~ ABC
CBD ~ ABC
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
11
12.
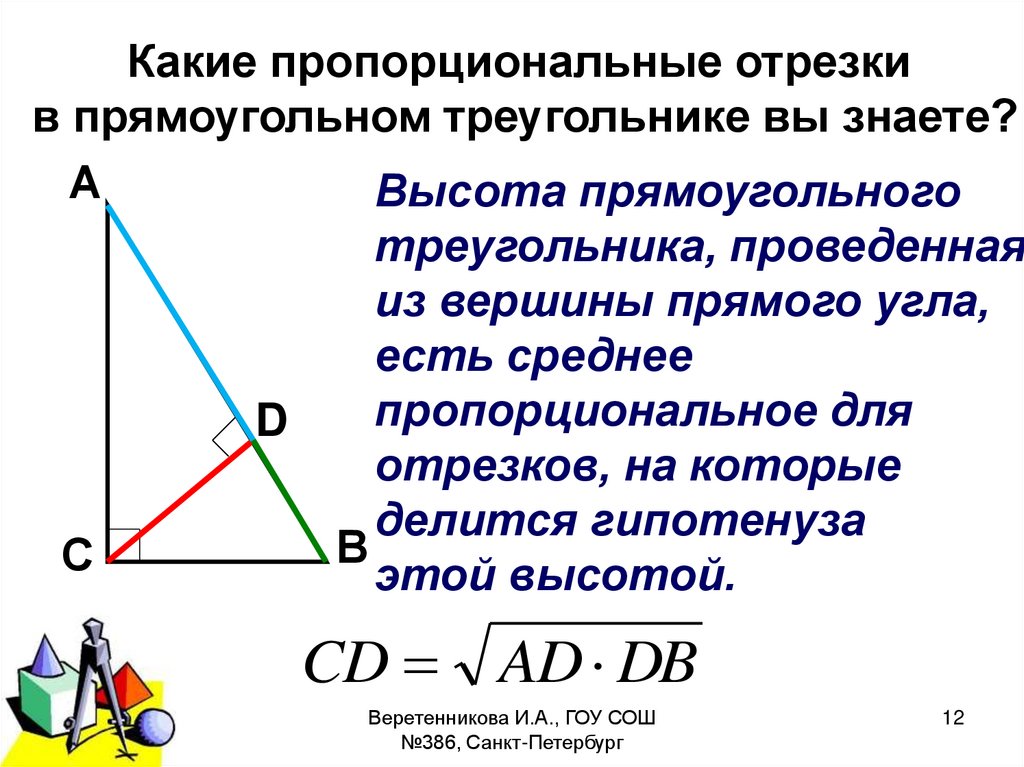
Какие пропорциональные отрезкив прямоугольном треугольнике вы знаете?
А
Высота прямоугольного
треугольника, проведенная
из вершины прямого угла,
есть среднее
пропорциональное для
D
отрезков, на которые
делится гипотенуза
В
С
этой высотой.
CD AD DB
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
12
13.
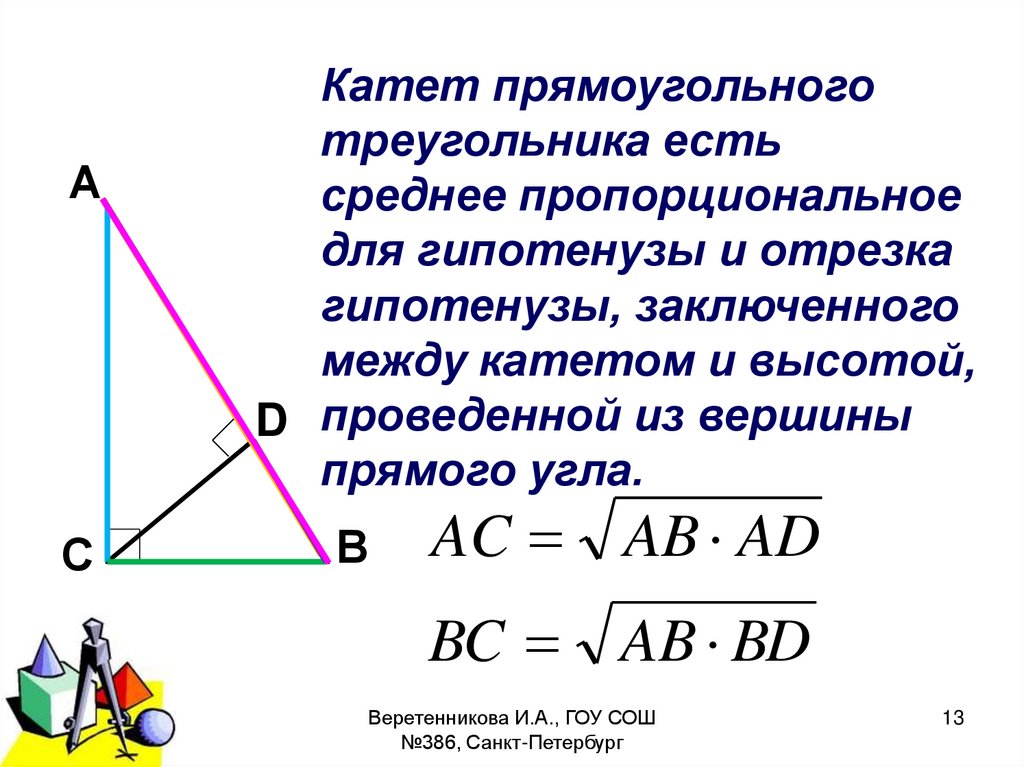
АС
Катет прямоугольного
треугольника есть
среднее пропорциональное
для гипотенузы и отрезка
гипотенузы, заключенного
между катетом и высотой,
D проведенной из вершины
прямого угла.
В
AC AB AD
BC AB BD
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
13
14.
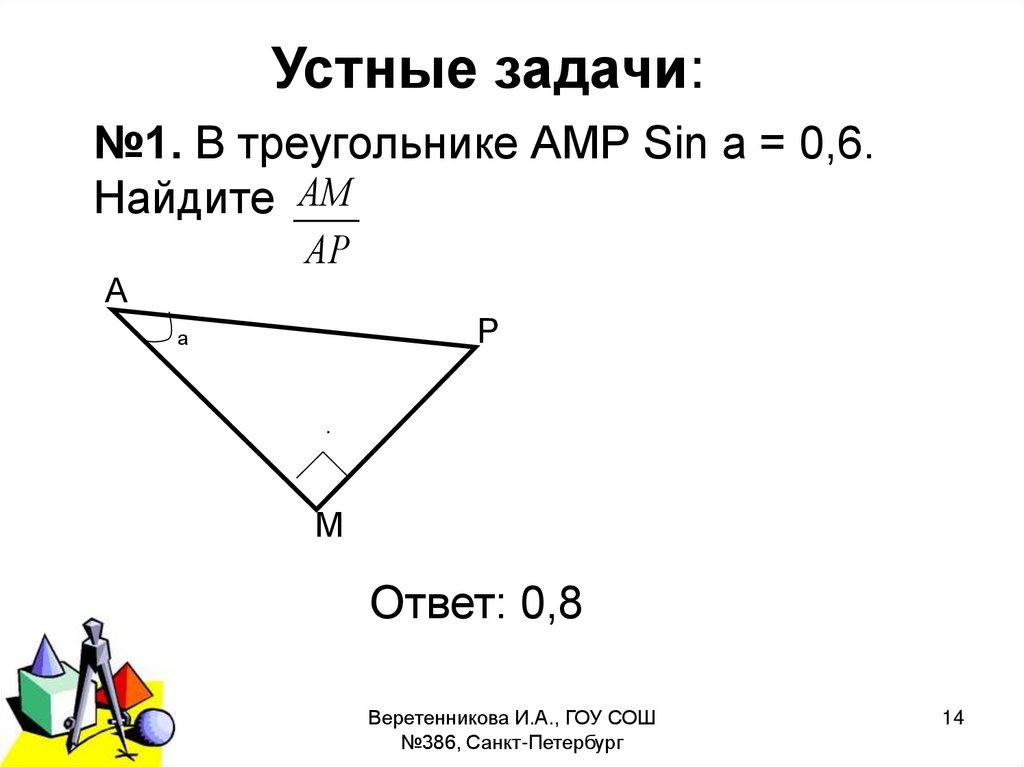
Устные задачи:№1. В треугольнике АМР Sin а = 0,6.
Найдите АМ
АР
А
Р
а
.
М
Ответ: 0,8
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
14
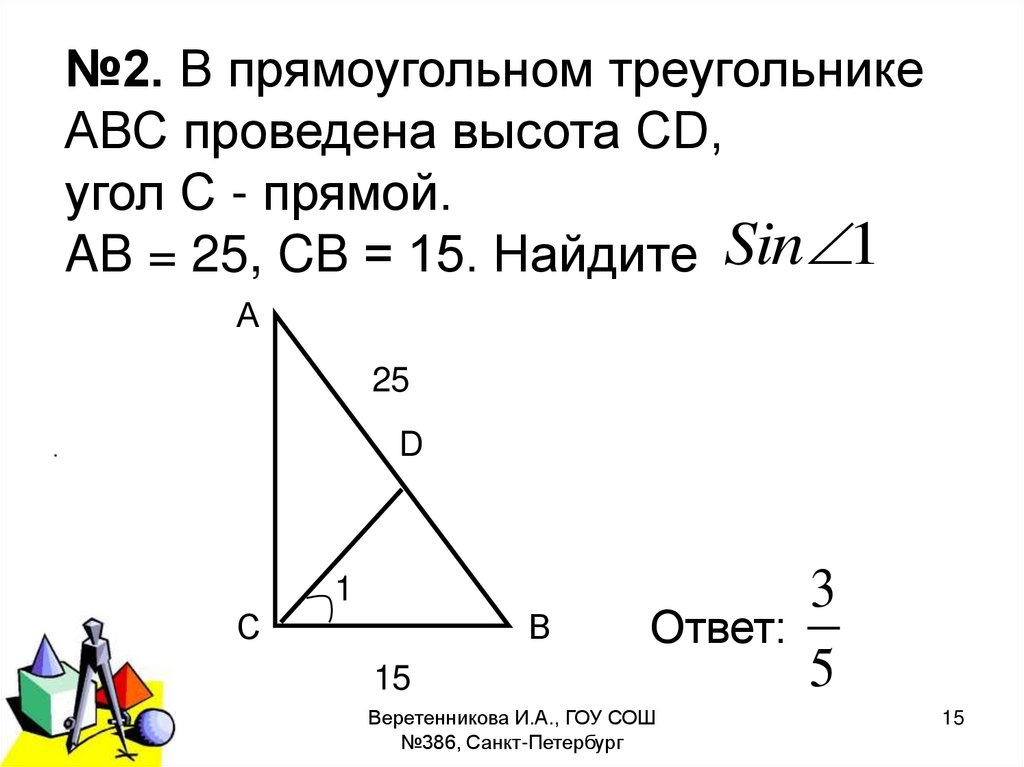
15.
№2. В прямоугольном треугольникеАВС проведена высота CD,
угол С - прямой.
AB = 25, CB = 15. Найдите Sin 1
А
25
D
.
1
С
В
15
2011 г.
3
Ответ:
5
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
15
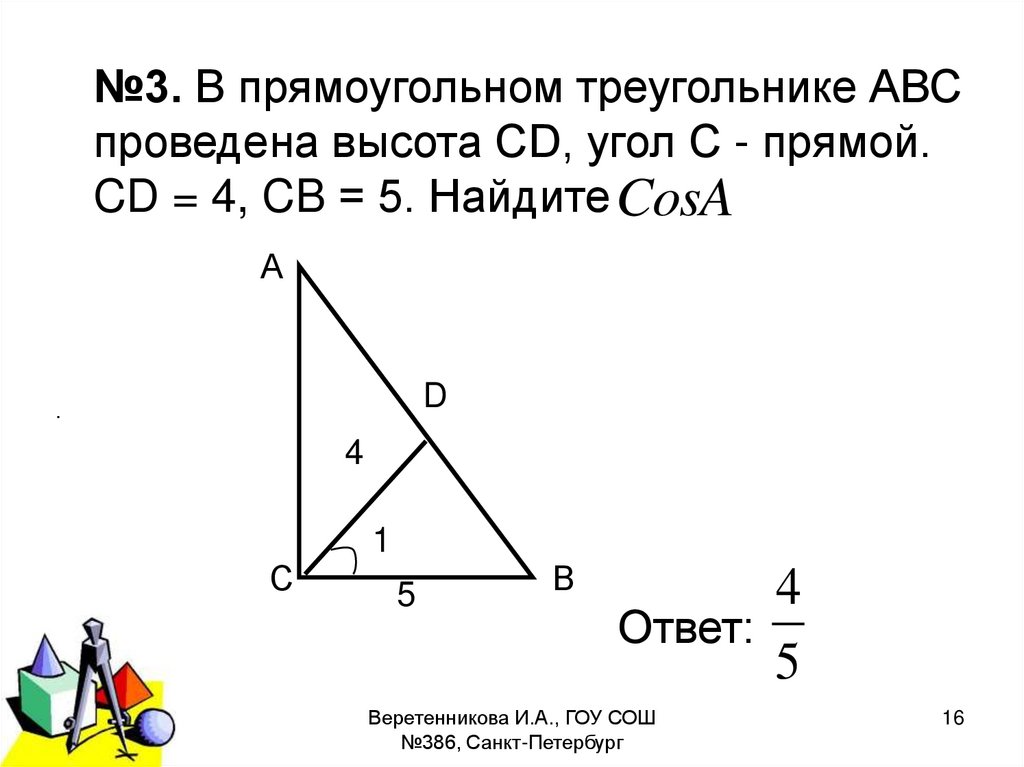
16.
№3. В прямоугольном треугольнике АВСпроведена высота CD, угол С - прямой.
CD = 4, CB = 5. Найдите CosA
А
D
.
4
1
С
2011 г.
5
В
4
Ответ:
5
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
16
17.
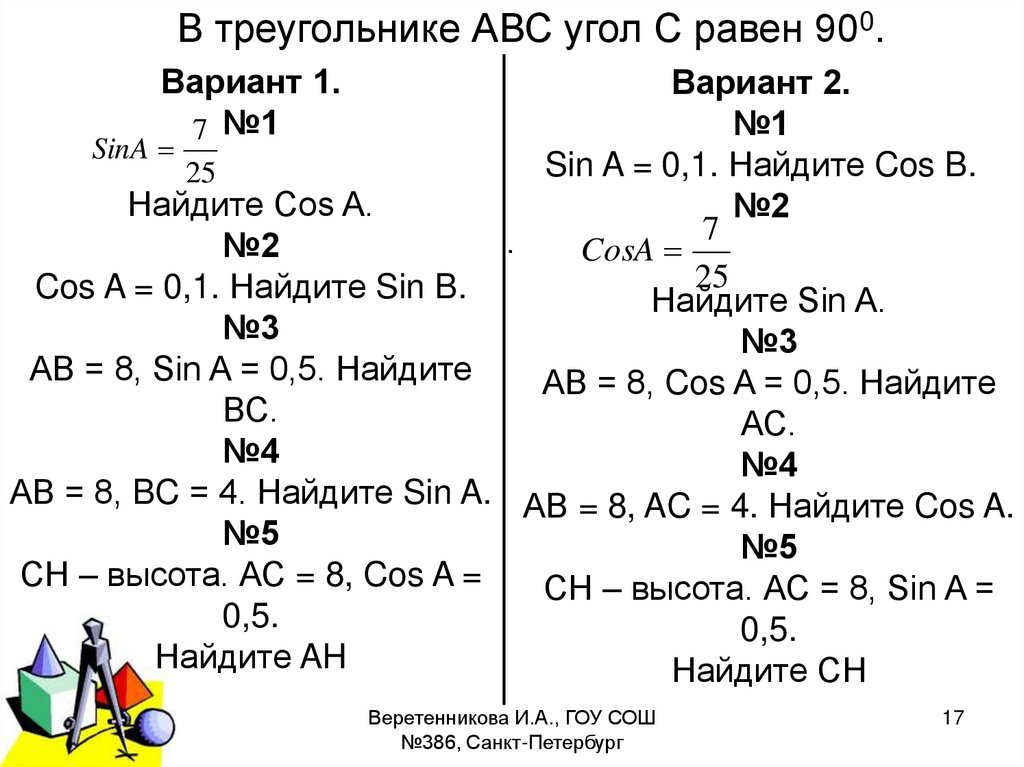
В треугольнике АВС угол С равен 900.Вариант 1.
7 №1
Вариант 2.
№1
SinA
Sin A = 0,1. Найдите Cos B.
25
Найдите Cos A.
№2
7
.
№2
CosA
25
Cos A = 0,1. Найдите Sin B.
Найдите Sin A.
№3
№3
АВ = 8, Sin A = 0,5. Найдите
АВ = 8, Cos A = 0,5. Найдите
ВС.
АС.
№4
№4
АВ = 8, BC = 4. Найдите Sin A. АВ = 8, AC = 4. Найдите Cos A.
№5
№5
СН – высота. АС = 8, Cos A =
СН – высота. АС = 8, Sin A =
0,5.
0,5.
Найдите AH
Найдите СН
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
17
18.
Ответы:Вариант 1: 1) 0,96; 2) 0,1; 3) 4; 4) 0,5; 5) 4.
Вариант 2: 1) 0,1; 2) 0,96; 3) 4; 4) 0,5; 5) 4.
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
18
19.
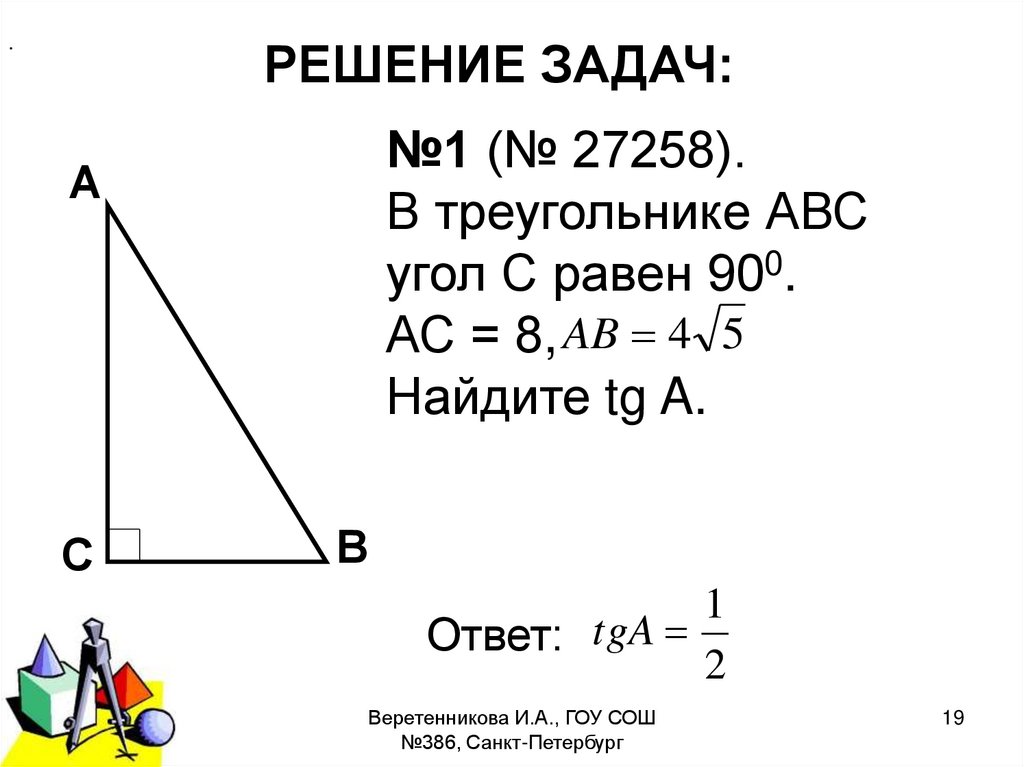
.РЕШЕНИЕ ЗАДАЧ:
№1 (№ 27258).
В треугольнике АВС
угол С равен 900.
АС = 8, AB 4 5
Найдите tg A.
А
С
В
1
Ответ: tgA
2
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
19
20.
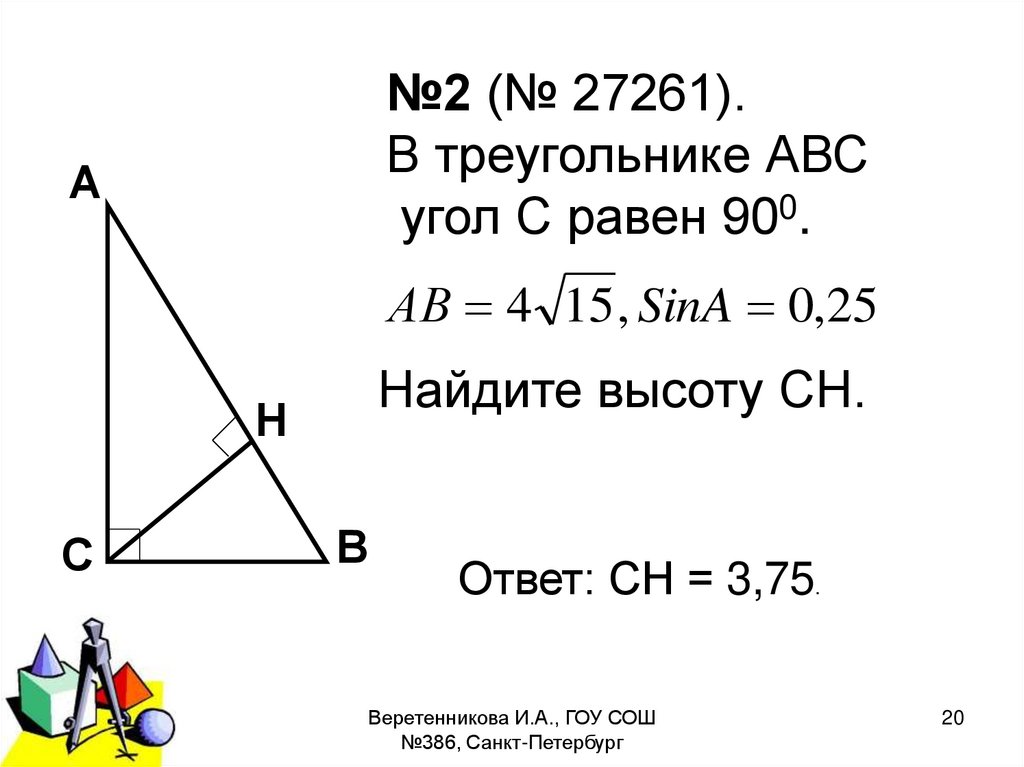
№2 (№ 27261).В треугольнике АВС
угол С равен 900.
А
АВ 4 15 , SinA 0,25
Найдите высоту СН.
Н
С
2011 г.
В
Ответ: СН = 3,75.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
20
21.
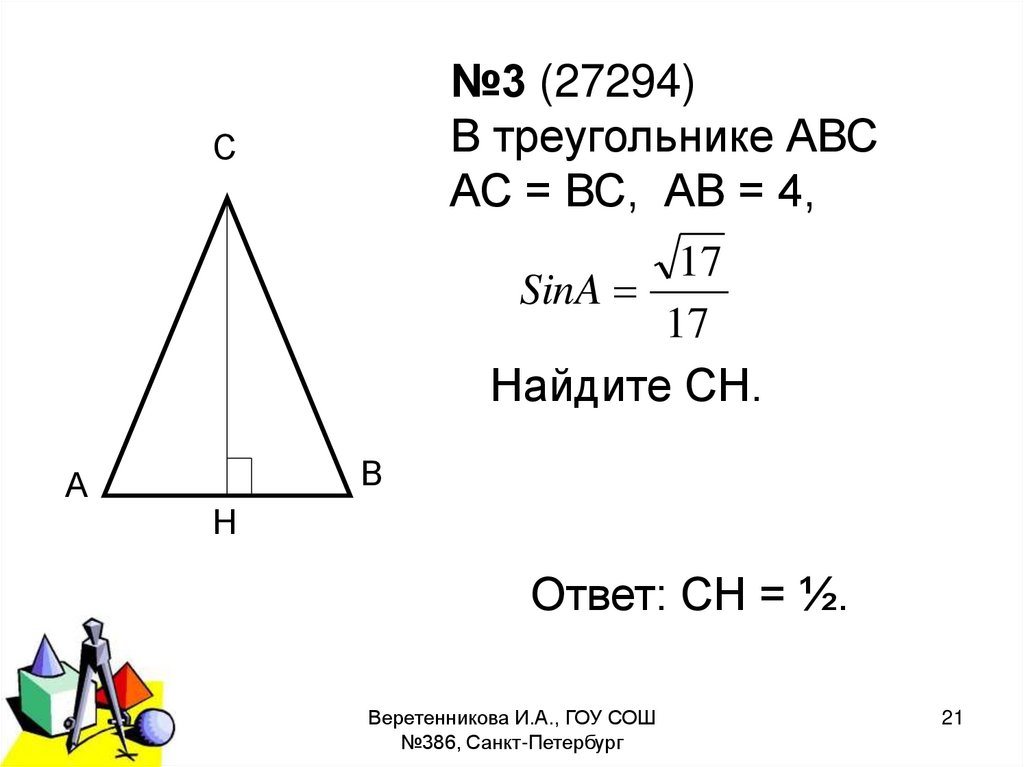
№3 (27294)В треугольнике АВС
АС = ВС, АВ = 4,
С
17
SinA
17
Найдите СН.
А
В
Н
Ответ: СН = ½.
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
21
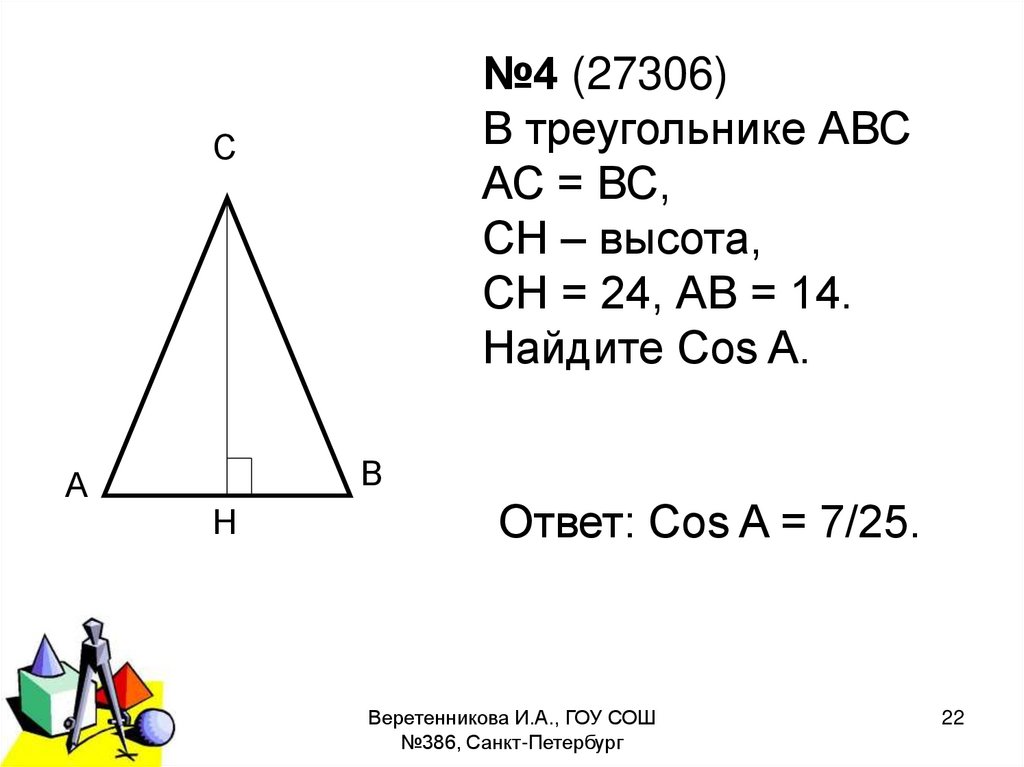
22.
№4 (27306)В треугольнике АВС
АС = ВС,
СН – высота,
СН = 24, АВ = 14.
Найдите Cos A.
С
А
2011 г.
В
Н
Ответ: Cos A = 7/25.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
22
23.
№5 (27282).В треугольнике АВС
угол С равен 900. СН
– высота, АС = 7,
А
tgA
Н
С
В
33
4 33
Найдите АН.
Ответ: АН = 4
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
.
23
24.
Подведение итогов урока.1) Какие трудности у вас возникли?
2) Какой теоретический материал
чаще всего используется при
решении задач на данную тему?
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
24
25.
2011 г.Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
25
26.
1) открытый банк задач ЕГЭ по математикеhttp://www.mathege.ru:8080/or/ege/Main.html;jsessionid=C9E96CF183B3
0C79B0DD925706ABCCAB?view=Pos
2) адрес картинки:
http://www.garnetvalleyschools.com/138020131951924
7/lib/1380201319519247/tools.gif
3) Л. С. Атанасян и др. Геометрия. 7-9 классы. Учебник для
общеобразовательных учреждений. Москва. Просвещение. 2010 г.
2011 г.
Веретенникова И.А., ГОУ СОШ
№386, Санкт-Петербург
26









 Математика
Математика








