Похожие презентации:
Дифференциальное исчисление
1.
Дифференциальноеисчисление
2.
Студент должен знатьОСНОВЫ ИНТЕГРАЛЬНОГО И
ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ*
* Федеральный государственный стандарт
среднего профессионального образования
по специальности 060501 Сестринское дело
3.
ПОНЯТИЕПРОИЗВОДНОЙ
ФУНКЦИИ
4.
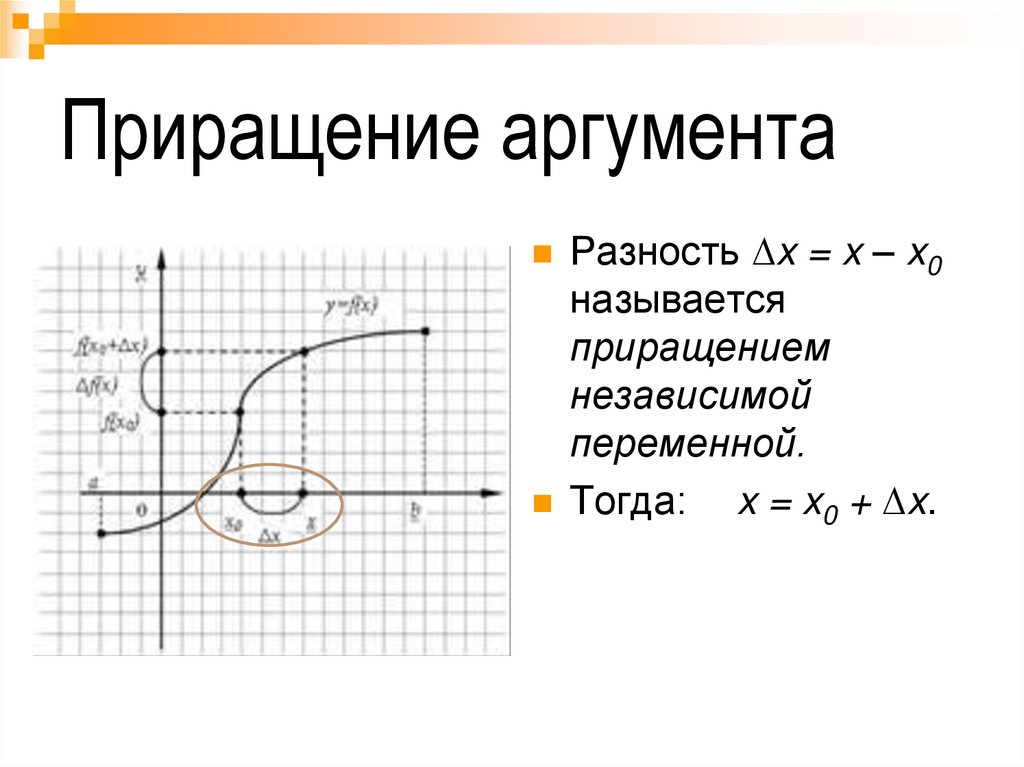
Приращение аргументаРазность ∆x = x – x0
называется
приращением
независимой
переменной.
Тогда: x = x0 + ∆x.
5.
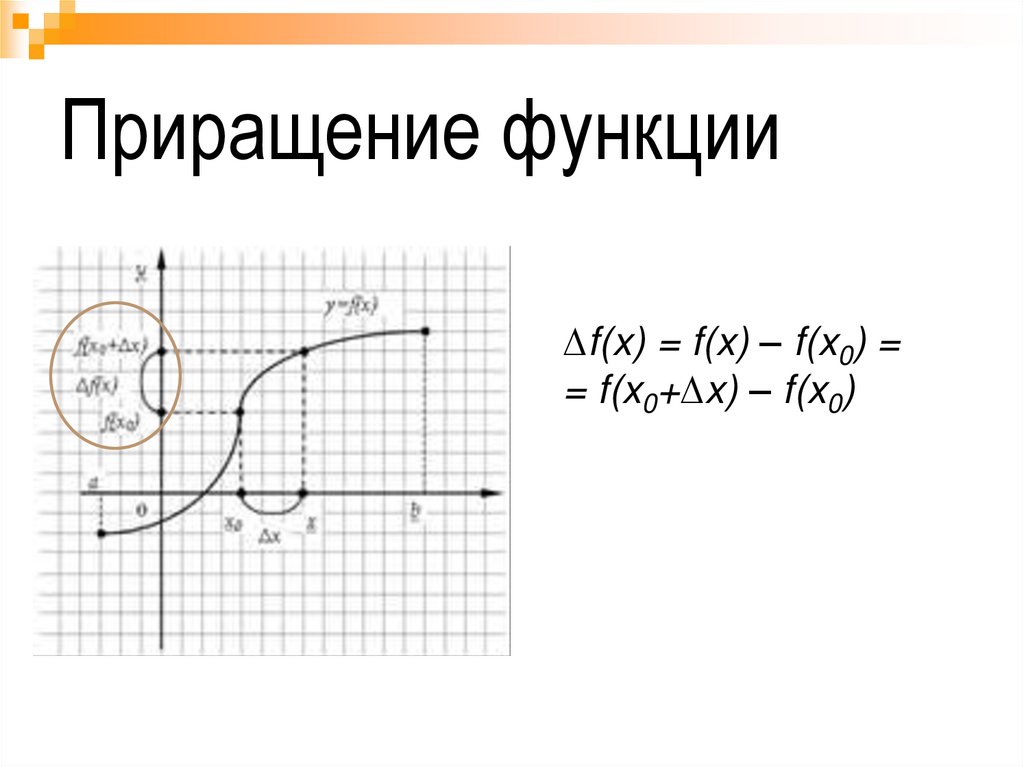
Приращение функции∆f(x) = f(x) – f(x0) =
= f(x0+∆x) – f(x0)
6.
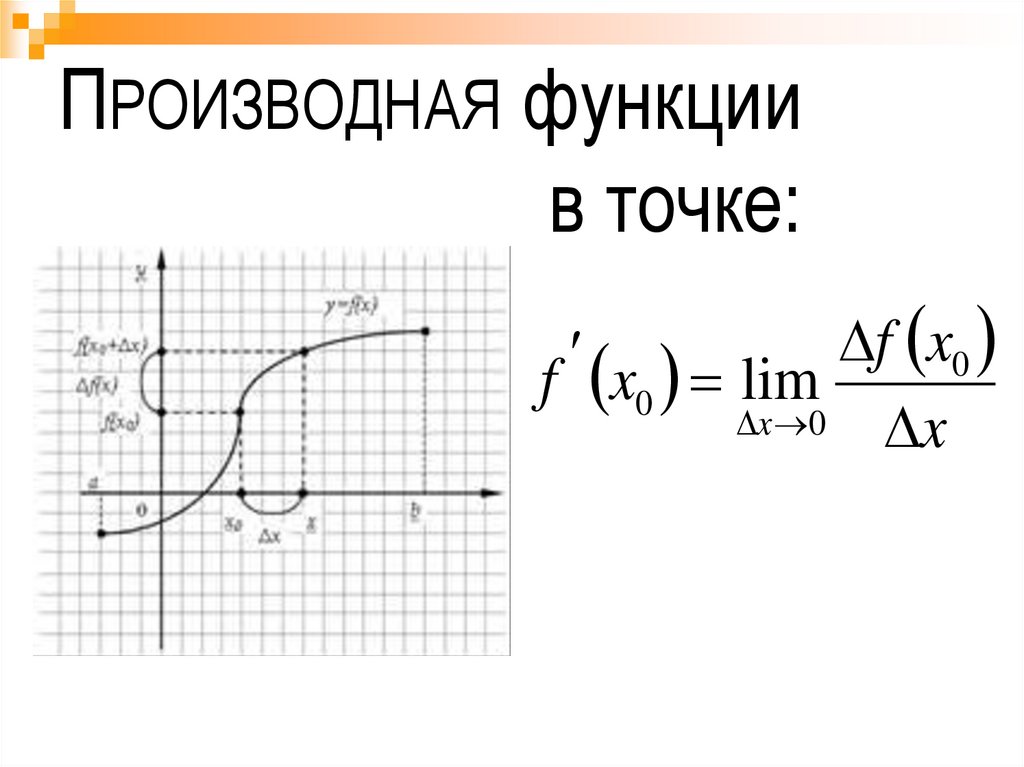
ПРОИЗВОДНАЯ функциив точке:
f x0
f x0 lim
x 0
x
7.
ПРОИЗВОДНАЯ функции1. (у = f(x), x = x0, f’(x0))
(у= f(x) – дифференцируема в точке x0)
2. Если у = f(x) дифференцируема в каждой
точке x из интервала X, то она называется
дифференцируемой на интервале X.
8.
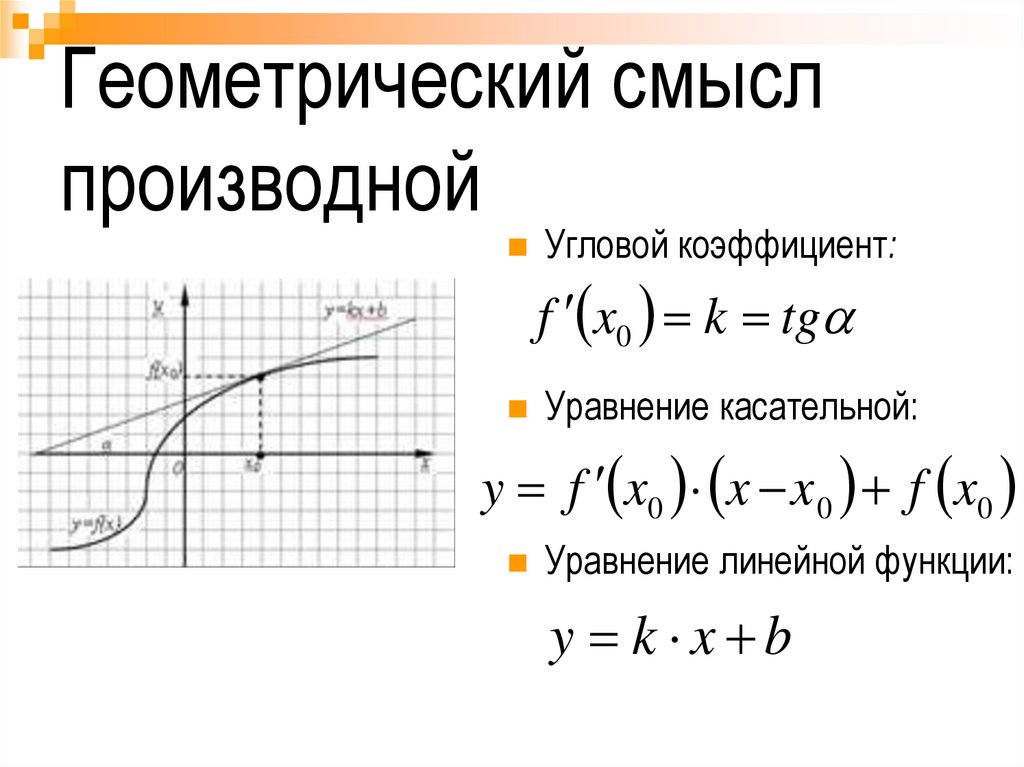
Геометрический смыслпроизводной
Угловой коэффициент:
f x0 k tg
Уравнение касательной:
y f x0 x x 0 f x0
Уравнение линейной функции:
y k x b
9.
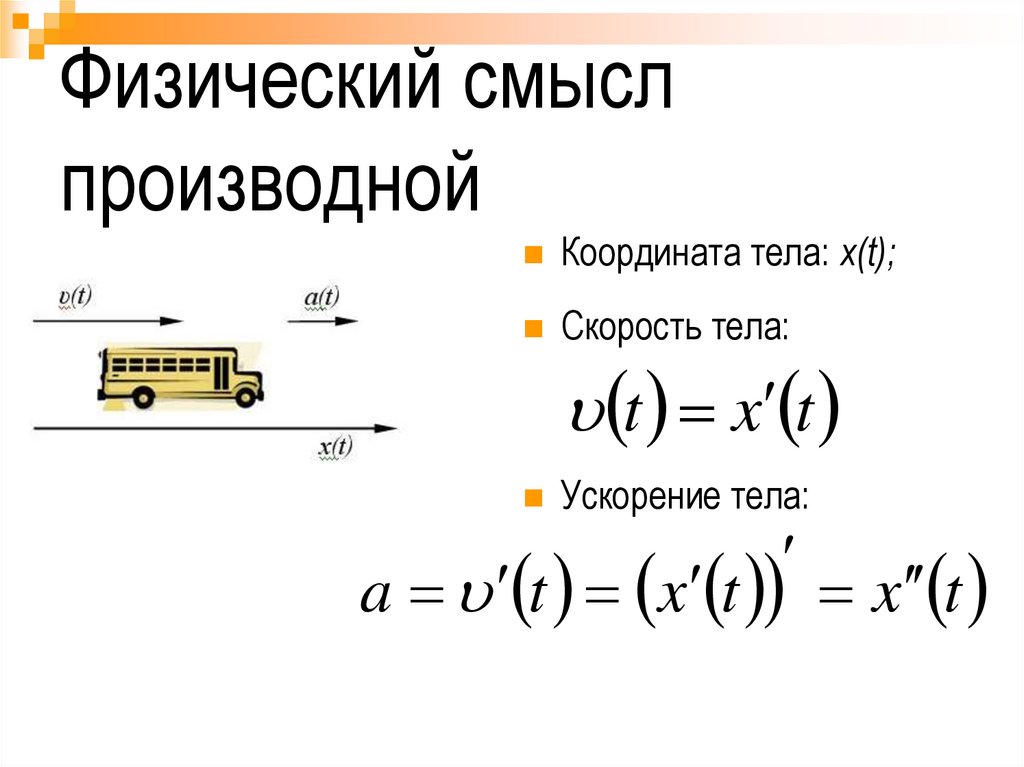
Физический смыслпроизводной
Координата тела: x(t);
Скорость тела:
Ускорение тела:
t x t
a t x t x t
10.
ТАБЛИЦА ПРОИЗВОДНЫХ11.
Степенная функцияC 0
x 1
x 2 x
2
x 3x
3
x n x
n
x 2
n 1
2
1
x
1
1
2
x
x
12.
Тригонометрическиефункции
sin x
cos x
1
tgx 2
cos x
1
ctgx 2
sin
x
cos x sin x
13.
Показательная илогарифмическая функции
e e
x
a a
x
x
x
ln a
1
ln x
x
1
log a x
x ln a
14.
ПРАВИЛАДИФФЕРЕНЦИРОВАНИЯ
15.
Производная суммы (Т1)u
u
16.
Вынос множителя за знакпроизводной (С1)
k u
k u
17.
Производнаяпроизведения (Т2)
u
u u
18.
Производная частного (Т3)u u u
,
0
2
19.
СЛОЖНАЯ ФУНКЦИЯИ ЕЁ ДИФФЕРЕНЦИРОВАНИЕ
20.
Сложная функцияy u
x
– сложная функция;
– сложный аргумент.
21.
Сложная функция y sin xy u sin
x x
2
– сложная
тригонометрическая
функция;
– сложный аргумент,
квадратичная функция.
2
22.
Производнаясложной функции (Т4)
u
u
23.
Прим. 1. Найти производнуюфункции: y 2 3 cos x 4 x
x
y 2 3 cos x 4 x
x
7
2 3 cos x 4 x
x
7
2 ln 2 3 cos x 4 x
x
6
2 ln 2 3 sin x 4 7 x
x
6
2 ln 2 3 sin x 28 x .
x
7
7
24.
Прим. 2. Найти производнуюфункции:
y x 3 x 2x
2
3
2 x 0 x 2 x x 3 3x 2 1
2 x x 2 x x 3 3x 2
y x 3 x 2 x
3
2
2
3
x 3 x 2x x 3 x 2x
2
3
3
2
3
2
2
2
2 x 4 x 3x 2 x 9 x 6
4
2
4
2
5 x 3 x 6.
4
2
2
25.
Прим. 3. Найти производную2
x 3
y 3
x 2x
функции:
x 3
y 3
x 2x
x
2
2
3 x3 2 x x 2 3 x3 2 x
x
2 x x 3 2 x x 2 3 3x 2 2
x
3
2x
2
3
2x
2
4
x
3
2x
2
2
2
2 x 4 x 3x 2 x 9 x 6
4
2
x 4 11x 2 6
x
3
2x
2
.
26.
Прим. 4. Найти производнуюфункции:
y
y 3x 5 x
3
3x 5 x
3
1
2 3x 5 x
3
9x 5
2
2 3x 5 x
3
3x 5 x
.
3
27.
ДИФФЕРЕНЦИАЛ ФУНКЦИИ28.
Дифференциал функцииПо определению
производной:
f x
y f x lim
.
x 0 x
При ∆x→0 – бесконечно малая величина.
При ∆x→0: ∆x = dx – дифференциал аргумента.
Дифференциал аргумента – очень малое его приращение.
Аналогично:
При ∆x→0: ∆f(x)→0 – бесконечно малая функция.
При ∆x→0: ∆f(x) = df(x) – дифференциал функции.
или: при ∆x→0: ∆y→0), ∆y = dy
Дифференциал функции – очень малое её приращение.
29.
Производная функцииТогда:
lim f x df x dy
f
x
y f x lim
x 0
.
x 0 x
lim x
dx
dx
df x
f x
dx
dy
y
dx
x 0
(читаем: «дэ эф от икс по дэ икс»).
(читаем: «дэ игрек по дэ икс») или:
30.
Дифференциал функцииИтак,
:
dy
y
dx
dy y dx
31.
Найти дифференциал3
y x .
функции
dy y dx
dx 3x dx
dy y dx x
.
Ответ:
3
2
dy 3x dx
2
32.
ПРИБЛИЖЕННЫЕВЫЧИСЛЕНИЯ
33.
Формула дляприближённых вычислений
f x f x0 x f x0 f x
Если х – малая величина, то х = dx и ∆f(x) = df(x)
f x f x0 dx f x0 df x
df x f x dx f x0 dx f x0 f x0 dx
f x 0 x f x 0 f ' x 0 x
34.
Вычислить:5
3,003 .
f x 0 x f x 0 f ' x 0 x
Рассмотрим функцию:
Так как х = 3,003, то
x0 3; x x x0 3,003 3 0,003.
5x ;
f x x
5
f 3 3 241.
f x x
5
4
4
f 3 5 3 5 81 405;
5
f 3,003 241 405 0,003 241 1,209 242,209.
35.
Вычислить:5
2,996 .
f x 0 x f x 0 f ' x 0 x
f x x ;
5
x0 3; x 2,996 3 0,004.
5x ;
f x x
5
f 3 3 241.
4
4
f 3 5 3 5 81 405;
5
f 2,996 241 405 0,004 241 2,0251
238,9749 238,975.
36.
ЧАСТНЫЕ СЛУЧАИПРИБЛИЖЁННЫХ
ВЫЧИСЛЕНИЙ
37.
n-я степень числа x 1x 1 1 n
n
x 1
n
0 1
38.
Корень n-й степени числаx 1
1
n
n
x 1 1
n
x 1 0 1
39.
51,003 .
Вычислить:
n
n
x 1 1 n
1,003 1 0,003 , n 5
1,003 1 0,003
1 5 0,003 1 0,015 1,015.
5
5
40.
Вычислить:n
4
0,996
1
x 1 1
n
n
0,996 1 0,004, n 4
4
0,996 4 1 0,004
1
1 0,004 1 0,001 0,999.
4
41.
ИтогиОпределение производной;
Таблица производных;
Правила дифференцирования;
Дифференциал функции;
Приближённые вычисления
дифференциала.
с помощью






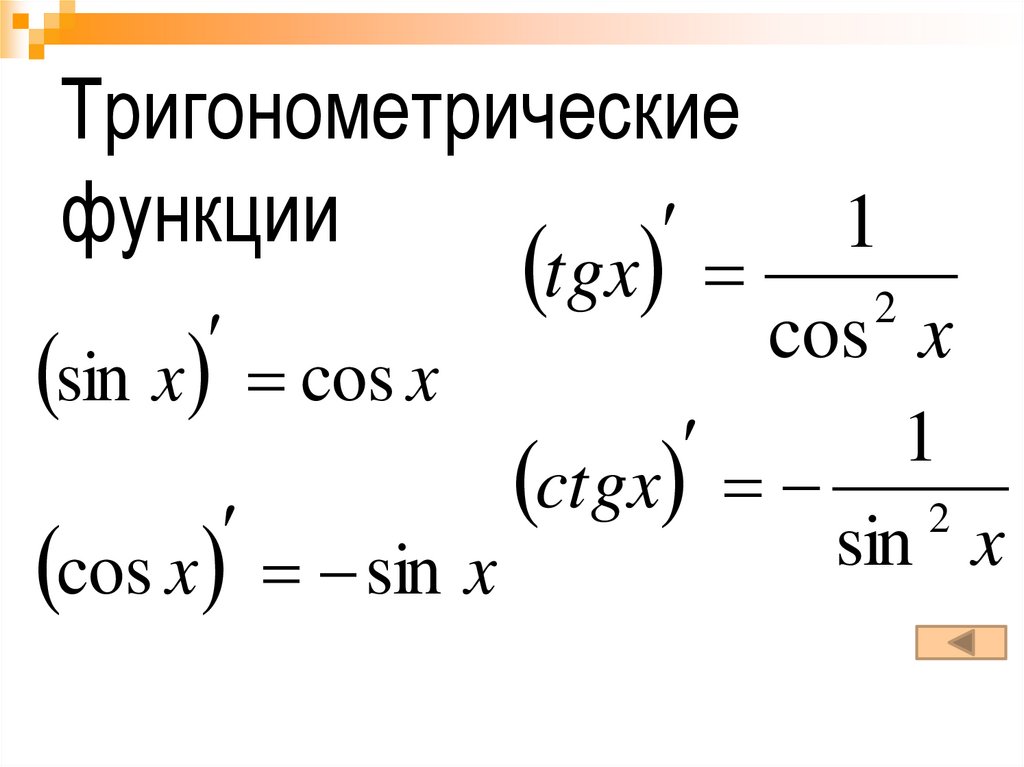


























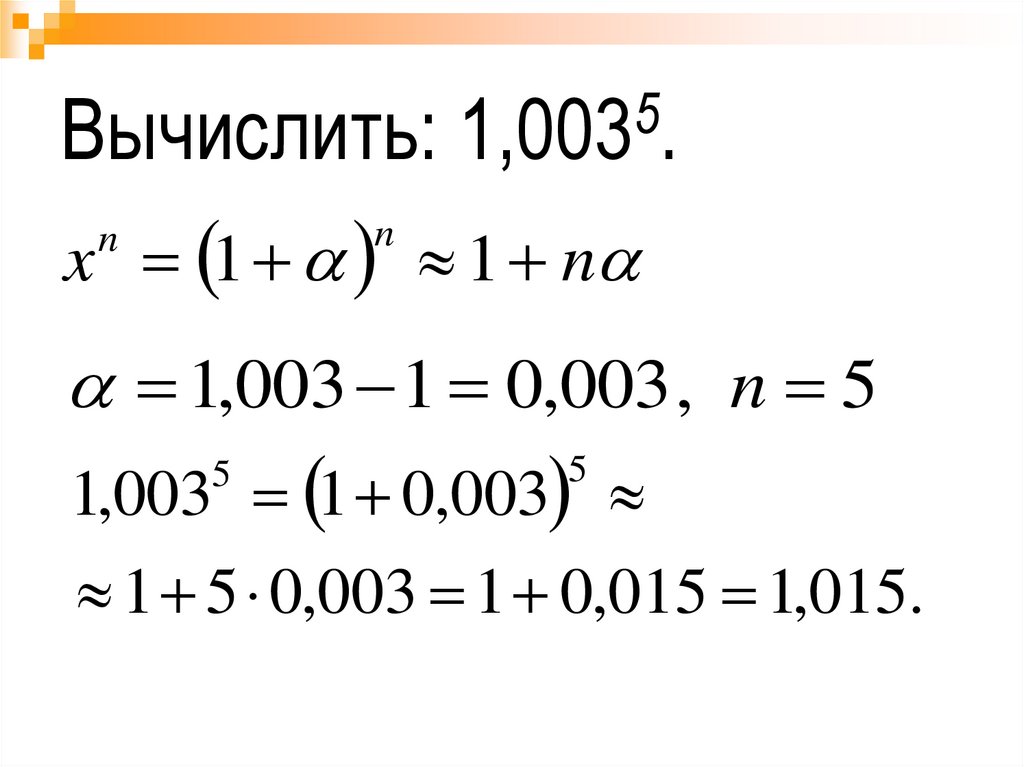


 Математика
Математика








