Электростатическое поле. Тема 3.2. Применение электростатической теоремы Гаусса

1.

Электростатическое поле
Электростатическая теорема Гаусса
3.2. Применение электростатической
теоремы Гаусса

2.

Различные формы записи теоремы Гаусса
Для дискретного распределения зарядов:
Фe E dS 4 ke qi
i
S
Для объёмного электрического заряда:
Фe E dS 4 ke dV
S
V
Дифференциальная (локальная форма записи):
div E 4 ke
Физико-технический факультет
2

3.

Линейное распределение
электрических зарядов
Расчет электростатического поля бесконечно длинной тонкой
равномерно заряженной нити:
dSосн. /
Фe E dS 4 k e dl
h
o
E
E
r
dSбок. r
S
L
/
Фe 2 E dS осн. E dS бок.
S осн.
S бок.
Фe 2 E / dS осн. 0 E dS бок. 1
S осн.
S бок.
Фe 0 E dS бок. E S бок. E 2 r h
sбок.
Физико-технический факультет
3

4.

Линейное распределение
электрических зарядов
Расчет электростатического поля бесконечно длинной тонкой
равномерно заряженной нити:
dSосн. /
Фe E dS 4 k e dl
h
o
E
E
r
dSбок. r
S
L
dl dl h
L
L
E 2 r h 4 k e h
2
E ke
r
Физико-технический факультет
4

5.

Линейное распределение
электрических зарядов
Электростатическое поле длинного равномерно заряженного
стержня:
Физико-технический факультет
5

6.

Поверхностное распределение
электрических зарядов
Расчет электростатического поля безграничной равномерно
заряженной плоскости:
Фe E dS 4 k e dS
dSбок.
/
E
E
E
r o r r
dSосн.
dSосн.
S
S
/
Фe E dS бок . 2 E dSосн .
S бок .
S осн .
Фe E / dS бок . 0 2 E dSосн . 1
S бок .
S осн .
Фe 0 2 E dSосн . 2 E Sосн .
sосн .
Физико-технический факультет
6

7.

Поверхностное распределение
электрических зарядов
Расчет электростатического поля безграничной равномерно
заряженной плоскости:
dSбок.
Фe E dS 4 k e dS
/
E
E
E
r o r r
dSосн.
dSосн.
S
dS
S
осн.
S
dSосн. Sосн.
S
2 E Sосн. 4 ke Sосн.
E 2 ke
Физико-технический факультет
7

8.

Поверхностное распределение
электрических зарядов
Электростатическое поле плоского конденсатора:
Физико-технический факультет
8

9.

Алгоритм расчёта полей с
применением теоремы Гаусса:
из соображений симметрии системы определяем форму
силовых линий поля;
выбираем удобную для нахождения потока форму
замкнутой поверхности;
находим поток вектора напряжённости
электростатического поля через эту поверхность;
находим суммарный электрический заряд, который
находится внутри этой поверхности;
подставляем полученные значения в теорему Гаусса и
находим напряжённость поля
Физико-технический факультет
9

10.

Объёмное распределение
электрических зарядов
Расчет электростатического поля безграничного равномерно
заряженного плоского слоя:
x a
div E 4 k e
a
o
a x
E x E y E z
4 k e
x
y
z
E y
E z
0
y
z
dE x 4 k e dx
Физико-технический факультет
dE x
4 k e
dx
E x 4 k e x
10

11.

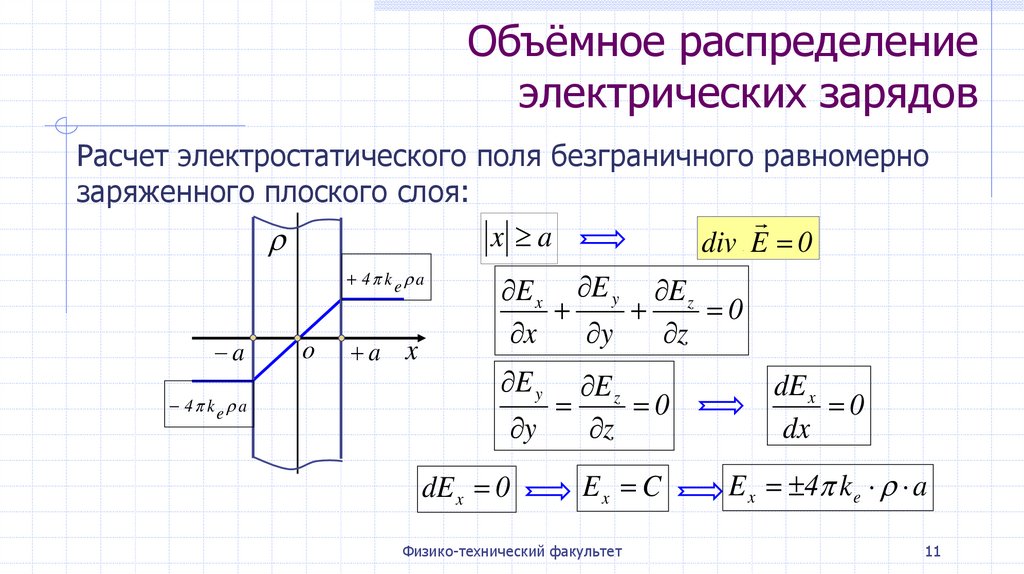
Объёмное распределение
электрических зарядов
Расчет электростатического поля безграничного равномерно
заряженного плоского слоя:
x a
div E 0
4 k e a
a
4 k e a
o
a x
E x E y E z
0
x
y
z
E y
E z
0
y
z
dE x 0
Ex C
Физико-технический факультет
dE x
0
dx
E x 4 k e a
11