Похожие презентации:
Электростатическое поле. Теорема Гаусса. Напряженность поля. Лекция 10.1
1.
Некоторые наиболее употребляемые буквыгреческого алфавита
Кафедра физики
- альфа
- бета
- гамма
- дельта,
- э псилон
- каппа - ро
- эта
- сигма
- ламбда - кси
- ми (мю) - дзета
- тета
- пси
- тау
- фи
Общая физика. "Термодинамика"
1
2.
Кафедра физикиЛЕКЦИЯ 10.1
Электростатика
План лекции
1. Электрический заряд. Свойства и законы;
2. Характеристики электрического поля:
- напряженность;
- потенциал.
3. Некоторые сведения из теории векторных полей.
4. Теорема Гаусса – Остроградского.
5. Вычисление полей с помощью теоремы Гаусса:
- поле бесконечной однородно заряженной плоскости;
1. - поле двух разноименно заряженных плоскостей;
2. - поле бесконечно протяженного заряженного цилиндра.
Общая физика. «Электростатика»
2
3.
Кафедра физикиЭлектростатика
Электростатика - раздел знаний об электричестве, в котором
изучаются взаимодействия и свойства систем электрических
зарядов, неподвижных относительно выбранной инерциальной
системы отсчёта.
Электростатическое поле. Электрический заряд
Электростатическое поле - частная форма электромагнитного
поля, представляющая собой вид материи, посредством которой
взаимодействуют неподвижные электрические заряды.
Электрический заряд - скалярная физическая величина,
определяющая интенсивность электромагнитного взаимодействия.
Заряд всех элементарных частиц одинаков по модулю и
представляет
собой
наименьший
электрический
заряд,
встречающийся в природе. Этот заряд называется элементарным
зарядом и обозначается символом e.
Общая физика. «Электростатика»
3
4.
Кафедра физикиЭлектростатика
Электростатическое поле. Электрический заряд
Свойства зарядов.
- заряды: положительные (протон) и отрицательные (электрон);
- всякий заряд q кратен e = 1.6*10-19 Кл ( заряд квантуется);
- во всех системах отсчета заряд тела или частицы имеет одно и то
же значение (инвариантность);
- заряд любой системы равен сумме зарядов составляющих эту
систему тел (частиц) (аддитивность);
Общая физика. «Электростатика»
4
5.
Кафедра физикиЭлектростатика
Закон сохранения электрического заряда:
Алгебраическая сумма электрических зарядов тел или частиц,
образующих электрически изолированную систему, не изменяется
при любых процессах, происходящих в этой системе.
Закон Кулона:
Сила электрического взаимодействия между двумя неподвижными
заряженными частицами в вакууме прямо пропорциональна
произведению их зарядов и обратно пропорциональна квадрату
расстояния между ними.
q1 q2
F k 2
r
k
1
4 0
8,99 109 9 109 м/Ф,
( 0 = 8,85 10-12 Ф/м)
Общая физика. «Электростатика»
5
6.
Кафедра физикиЭлектростатика
Электростатическое поле. Характеристики
Количественными характеристиками электростатического поля
являются напряженность и потенциал.
Напряженность электрического поля.
e
r
+ r
q
F
qпр
q - неподвижный точечный заряд;
qпр - пробный (точечный, не вносящий искажения) заряд;
r – радиус-вектор;
- орт радиус-вектора.
er
На пробный заряд действует сила
Общая физика. «Электростатика»
1 q
F qпр
e
2 r
4 0 r
6
7.
Кафедра физикиЭлектростатика
Электростатическое поле. Характеристики
1 q
F qпр
e
2 r
4 0 r
Отношение F qпр для всех пробных зарядов будет одно и то же и
зависит лишь от величин, определяющих само поле, т.е. от q и r .
Поэтому отношение F qпр принимается
характеризующую электрическое поле:
F
E
qпр
за
величину,
- напряженность электрического поля в
точке, в которую помещен пробный заряд.
Общая физика. «Электростатика»
7
8.
Кафедра физикиЭлектростатика
Электростатическое поле. Характеристики
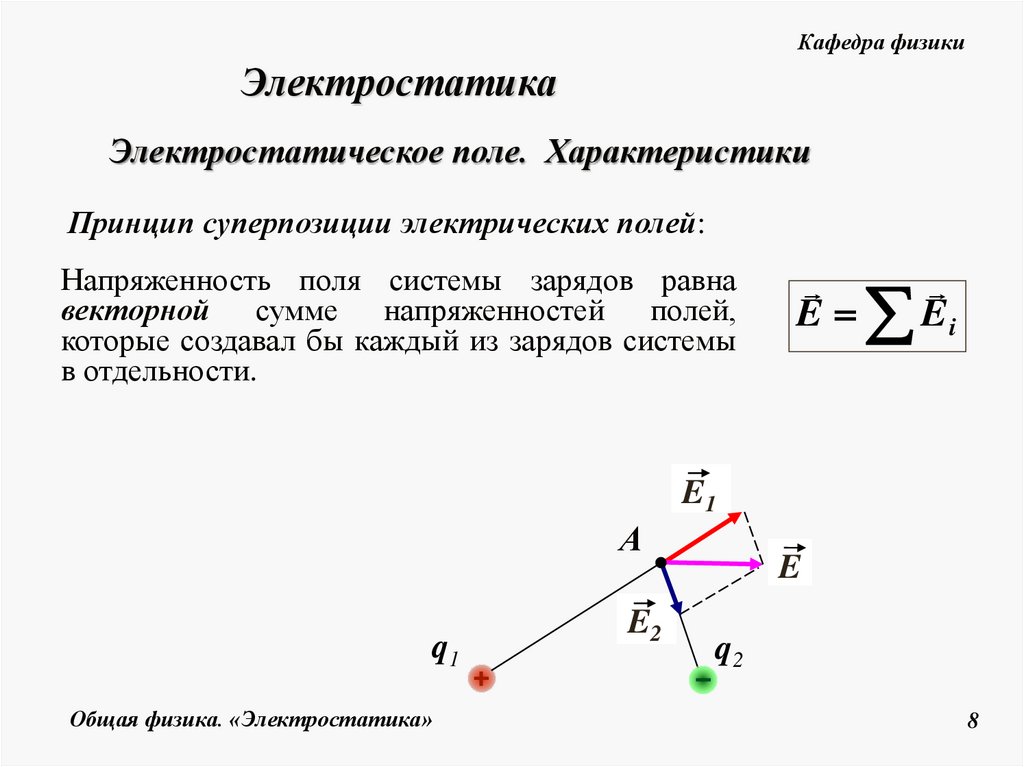
Принцип суперпозиции электрических полей:
Напряженность поля системы зарядов равна
векторной сумме напряженностей полей,
которые создавал бы каждый из зарядов системы
в отдельности.
E
Ei
E1
А
q1
Общая физика. «Электростатика»
E2
E
q2
8
9.
Кафедра физикиЭлектростатика
Электростатическое поле. Характеристики
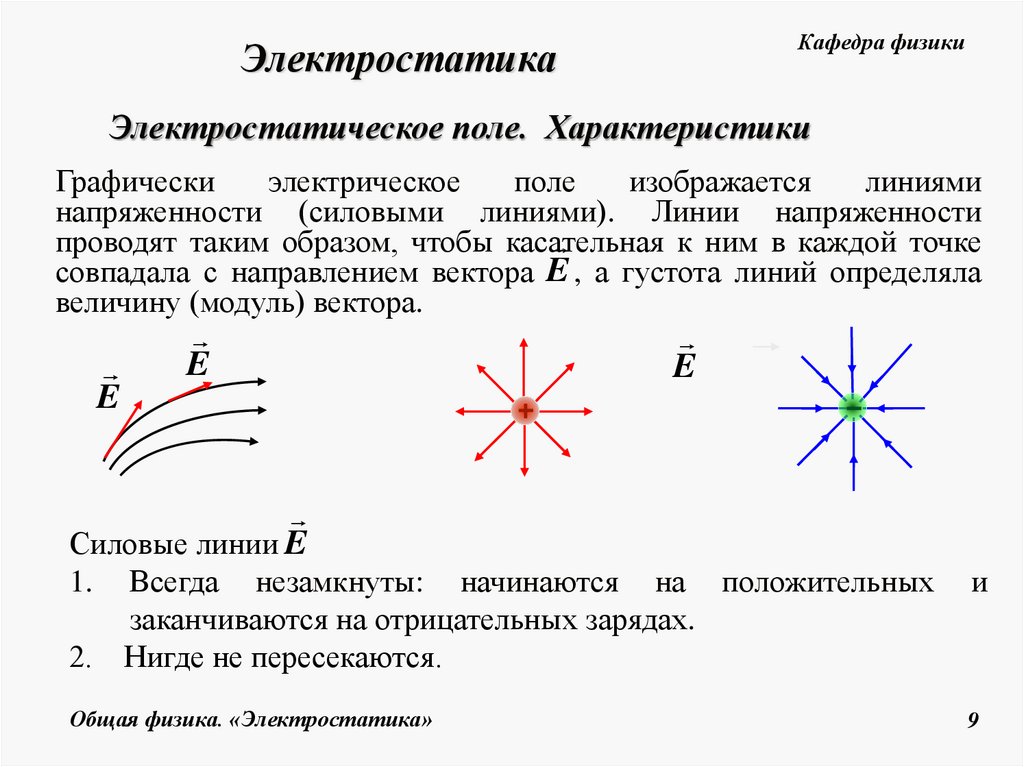
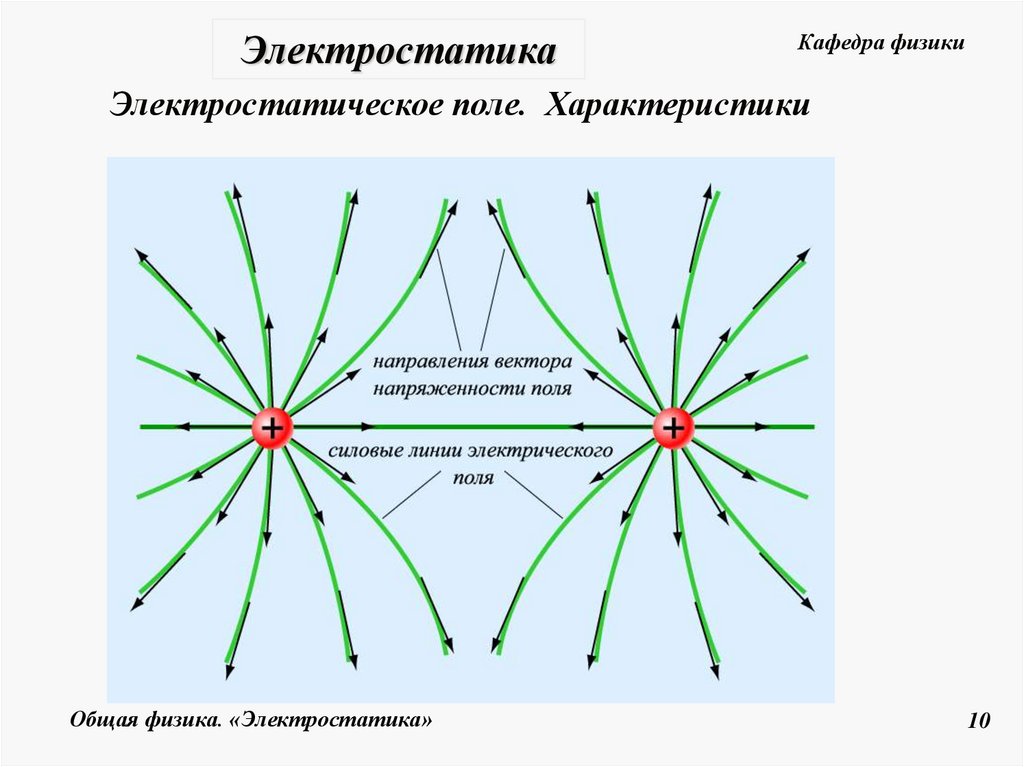
Графически
электрическое
поле
изображается
линиями
напряженности (силовыми линиями). Линии напряженности
проводят таким образом, чтобы касательная
к ним в каждой точке
совпадала с направлением вектора E , а густота линий определяла
величину (модуль) вектора.
E
E
E
Силовые линии E
1.
2.
Всегда незамкнуты: начинаются на положительных
заканчиваются на отрицательных зарядах.
Нигде не пересекаются.
Общая физика. «Электростатика»
и
9
10.
ЭлектростатикаКафедра физики
Электростатическое поле. Характеристики
Общая физика. «Электростатика»
10
11.
Кафедра физикиТеорема Гаусса-Остроградского
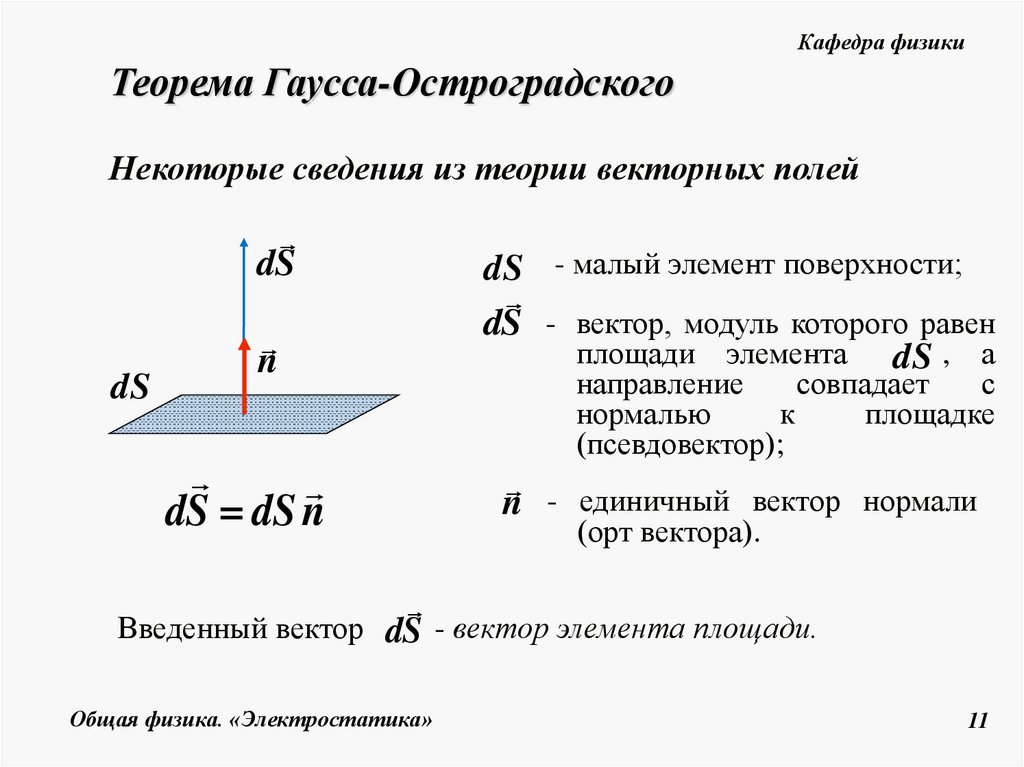
Некоторые сведения из теории векторных полей
dS
dS
n
dS - малый элемент поверхности;
dS - вектор, модуль которого равен
площади элемента dS , а
dS dS n
- единичный вектор нормали
n
направление
совпадает
с
нормалью
к
площадке
(псевдовектор);
(орт вектора).
Введенный вектор dS - вектор элемента площади.
Общая физика. «Электростатика»
11
12.
Кафедра физикиТеорема Гаусса-Остроградского
Некоторые сведения из теории векторных полей
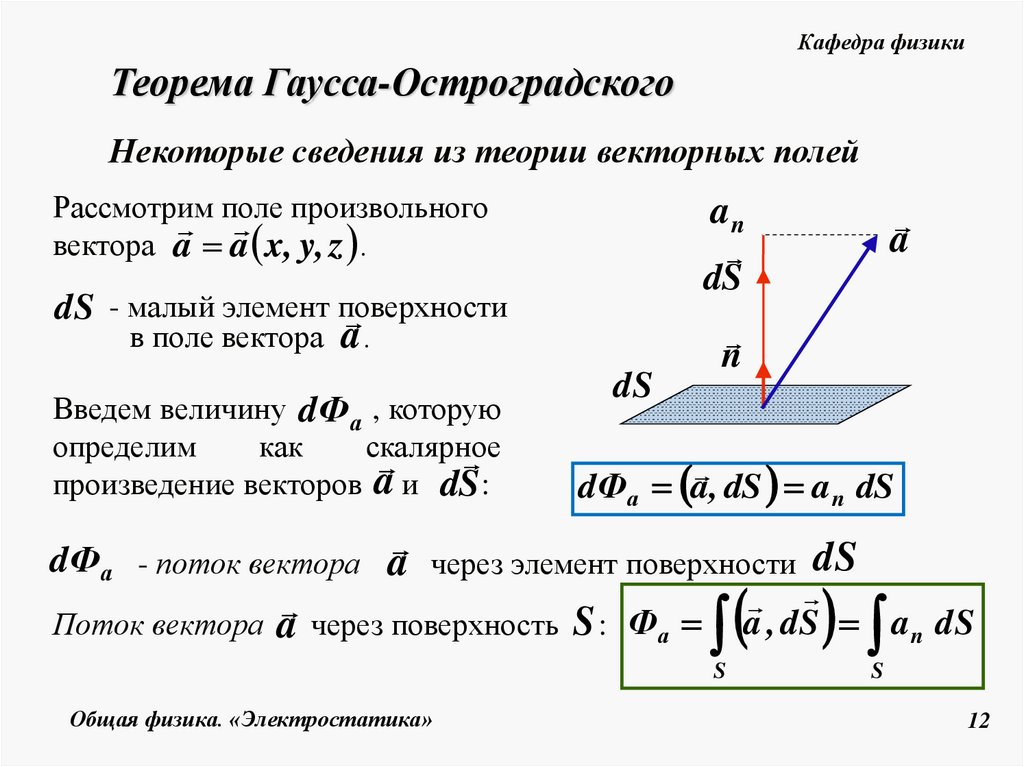
Рассмотрим поле произвольного
вектора a a x, y, z .
dS - малый элемент поверхности
в поле вектора a .
Введем величину dФа , которую
определим
как
скалярное
произведение векторов a и dS :
dS
an
dS
n
a
dФа a, dS a n dS
dФа - поток вектора a через элемент поверхности dS
Поток вектора a через поверхность S : Фа a , dS a n dS
S
Общая физика. «Электростатика»
S
12
13.
Кафедра физикиТеорема Гаусса-Остроградского
Некоторые сведения из теории векторных полей
Потоки векторных полей через замкнутые поверхности
S
dS
n
Положительными будут потоки dФа ,
выходящие из замкнутой поверхности
Входящие потоки – отрицательные
Суммарный поток вектора поля через
замкнутую поверхность определяется
интегралом по замкнутой поверхности:
Фа a, dS
S
Общая физика. «Электростатика»
13
14.
Кафедра физикиТеорема Гаусса-Остроградского
Поток ФЕ вектора напряженности электрического поля E сквозь
произвольную замкнутую поверхность S пропорционален
электрическому заряду q , заключенному внутри S.
Теорема в интегральной форме:
q
( E , dS )
S
0
Множитель (диэлектрическая проницаемость среды) учитывает
влияние свойств однородной среды на значение вектора
напряженности, 0=8,85·10-12 Ф/м – электрическая постоянная.
Теорема Гаусса в дифференциальной форме:
q
div E
0
ρq dq dV - объемная плотность заряда (отношение заряда dq
к малому объему dV, в котором заключен этот заряд).
Общая физика. «Электростатика»
14
15.
Кафедра физикиИспользуются физические величины: поверхностная и линейная
плотности зарядов.
Если заряд dq сосредоточен в тонком поверхностном слое, его
распределение
можно
характеризовать
поверхностной
плотностью x , y , z (сигма).
dq
σ
dS
dq - заряд, заключенный в слое площадью dS .
Общий заряд q определяется вычислением
интеграла по поверхности dS :
q σ x, y, z dS
S
Заряд может быть распределен вдоль некоторой линии (нить, тонкий
стержень и т.д.). В таком случае его распределение в пространстве
описывается линейной плотностью τ q (заряд, отнесенный к единице
длины заряженной линии l :
dq
τ q x, y, z
dl
Общая физика. "Электростатика"
Общий заряд q вычисляется
интегрированием:
q τ q dl
l
15
16.
Кафедра физикиЕсли объемная, поверхностная, и линейная плотности не зависят
от координат, то распределение заряда называется однородным.
Тогда
q q V
q S
q q l
Физический смысл теоремы Гаусса.
Теорема Гаусса выражает закон создания электрических полей
неподвижными электрическими зарядами. В интегральной форме
закон выражен применительно к замкнутой поверхности конечных
размеров, в дифференциальной форме – применительно к точке.
Общая физика. "Электростатика"
16
17.
Кафедра физикиВычисление электростатических полей с помощью
теоремы Гаусса
1. Поле бесконечной однородно заряженной плоскости
Пусть поверхностная плотность положительного заряда во всех
точках плоскости одинакова и равна σ.
E
E
Напряженность поля E в любой точке
имеет направление, перпендикулярное к
плоскости.
Очевидно,
что
в
симметричных
относительно
плоскости
точках
напряженность поля одинакова по
модулю и противоположно направлена.
Общая физика. "Электростатика"
17
18.
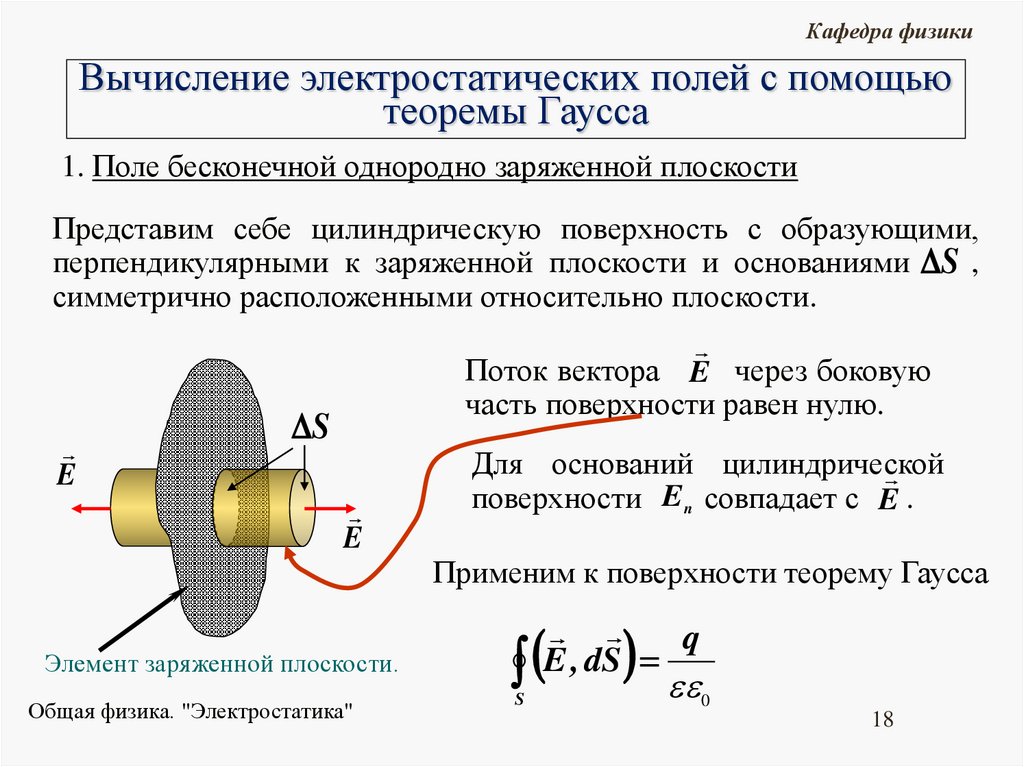
Кафедра физикиВычисление электростатических полей с помощью
теоремы Гаусса
1. Поле бесконечной однородно заряженной плоскости
Представим себе цилиндрическую поверхность с образующими,
перпендикулярными к заряженной плоскости и основаниями S ,
симметрично расположенными относительно плоскости.
E
Поток вектора E через боковую
часть поверхности равен нулю.
S
E
Для оснований цилиндрической
поверхности En совпадает с E .
Применим к поверхности теорему Гаусса
Элемент заряженной плоскости.
Общая физика. "Электростатика"
q
E , dS
S
0
18
19.
Кафедра физикиВычисление электростатических полей с помощью
теоремы Гаусса
1. Поле бесконечной однородно заряженной плоскости
S
E
E
Поскольку во всех точках поверхности,
пронизываемой полем, вектор напряженности
поля перпендикулярен к поверхности и одинаков
по величине, интеграл вычисляется легко:
E , dS E S
S
Суммарный поток через поверхность равен 2 E S
Учитывая, что q S, получим 2 E S S 0 . Окончательно:
E
2 0
Полученный результат не зависит от длины
цилиндра. Это означает, что на любом расстоянии от
плоскости напряженность поля одинакова.
Общая физика. "Электростатика"
19
20.
Кафедра физикиВычисление электростатических полей с помощью
теоремы Гаусса
2. Поле двух разноименно заряженных плоскостей.
Две параллельные бесконечные плоскости заряжены разноименно с
одинаковой по величине поверхностной плотностью .
E
E
E
E
E
Электрическое
поле
в
системе
определятся
суперпозицией
полей
каждой из пластин.
E
В области между плоскостями поля
имеют
одинаковое
направление,
следовательно,
результирующая
напряженность равна
E
2 0 2 0 0
Вне объема, ограниченного плоскостями, результирующая E 0 .
Таким образом, поле однородно и сосредоточено между плоскостями.
Общая физика. "Электростатика"
20
21.
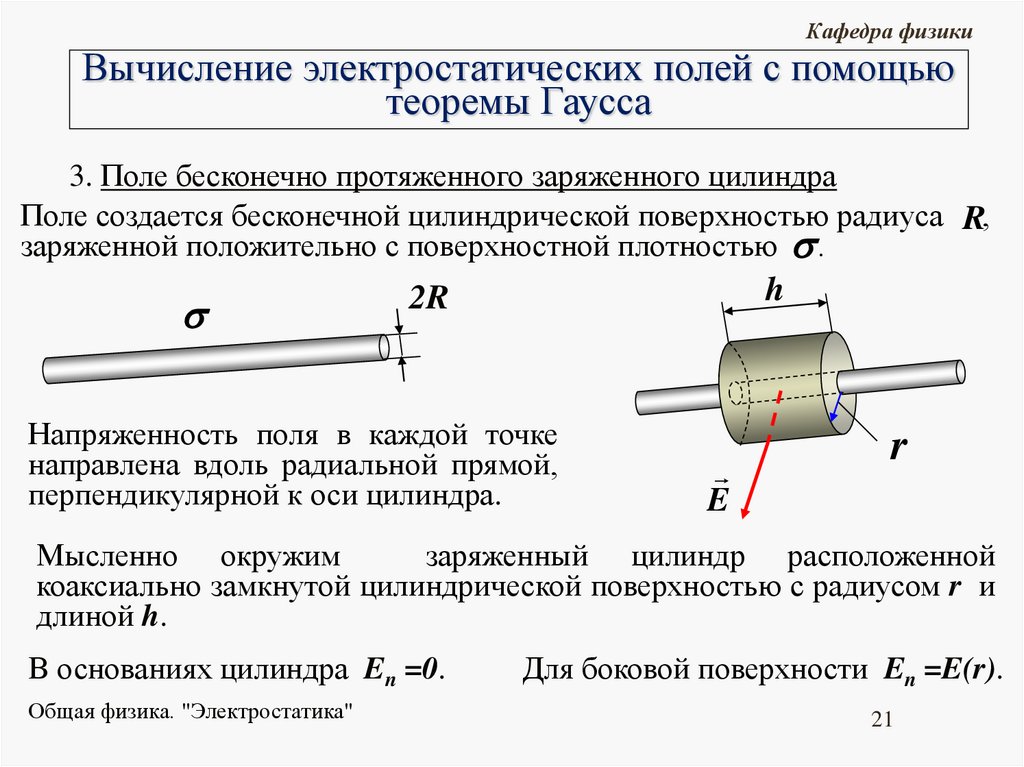
Кафедра физикиВычисление электростатических полей с помощью
теоремы Гаусса
3. Поле бесконечно протяженного заряженного цилиндра
Поле создается бесконечной цилиндрической поверхностью радиуса R,
заряженной положительно с поверхностной плотностью .
h
2R
Напряженность поля в каждой точке
направлена вдоль радиальной прямой,
перпендикулярной к оси цилиндра.
E
r
Мысленно окружим
заряженный цилиндр расположенной
коаксиально замкнутой цилиндрической поверхностью с радиусом r и
длиной h.
В основаниях цилиндра En =0.
Общая физика. "Электростатика"
Для боковой поверхности En =E(r).
21
22.
Кафедра физикиВычисление электростатических полей с помощью
теоремы Гаусса
3. Поле бесконечно протяженного заряженного цилиндра
Поток вектора E через эту поверхность равен E r 2 rh. При
внутрь поверхности попадает заряд q h .
E r 2 rh
Применим теорему Гаусса, получим:
Из этой формулы следует:
E r
1
2 0 r
r R
Если
r R
1
0
r R
h
E r 0
Поле отрицательно заряженного цилиндра будет отличаться
только направлением вектора E.
Таким образом, электрическое поле, создаваемое бесконечно
протяженным
заряженным
цилиндром
в
окружающем
пространстве, зависит от расстояния от цилиндра и линейной
плотности заряда.
Общая физика. "Электростатика"
22
23.
Кафедра физикиВычисление электростатических полей с помощью
теоремы Гаусса
Расчеты полей, созданных рассмотренными фигурами, имеют
сходство: во всех точках поверхности, которые пронизываются
полем, вектор напряженности перпендикулярен к поверхности и
поток вектора напряженности поля может быть выражен простой
формулой:
E , dS E S
S
Это значительно упрощает применение теоремы Гаусса.
Общая физика. "Электростатика"
23
















 Физика
Физика








