Математический анализ. Лекция №8. Производная функции одной переменной

1.

Математический анализ
ЛЕКЦИЯ № 8
ПРОИЗВОДНАЯ ФУНКЦИИ ОДНОЙ
ПЕРЕМЕННОЙ

2.

§ 1. Производная
Пусть в окрестности т. x 0 , включая x 0 , задана функция y f x . Дадим в т. x 0
аргументу
x приращение x (положительное или отрицательное). Тогда
y f x0 x f x0 .
y
, то его называют производной функции
x 0 x
Определение 1. Если существует lim
y f x в т. x 0 , или говорят, что y f x дифференцируема в т. x 0 , и обозначают:
y
f x , y x ,
dy df x
,
, т.е.
dx
dx
f x0 x f x0
(1)
x 0
x
Если в (1) x 0 и x 0 x 0 , то (1) называют правой - f пр x0 [левой f x0 lim
f л x0 ] производной в т. x 0 . Очевидно, что если f пр x0 , f л x0 и f пр f л , то f x0 .
Определение 2. Функция y f x называется дифференцируемой на отрезке a; b , если
она имеет производную в каждой точке
соответственно f пр a и f л b .
a; b , a на концах a и b существуют
Класс функций дифференцируемых в области D обозначается C D .
1

3.

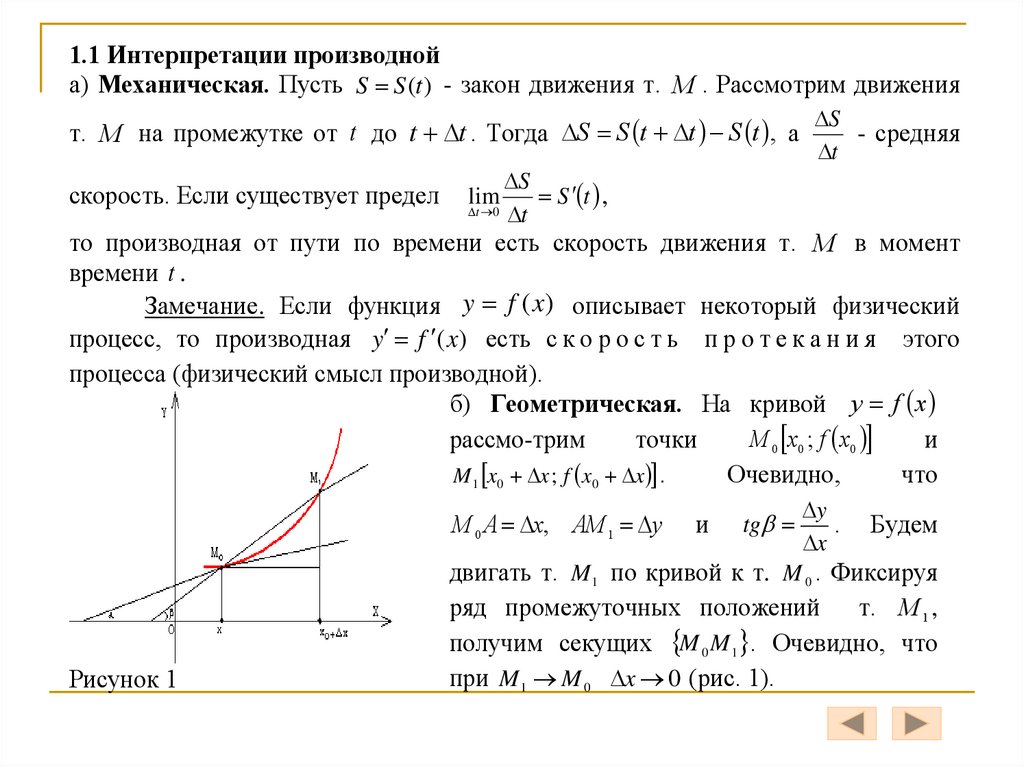
1.1 Интерпретации производной
а) Механическая. Пусть S S (t ) - закон движения т. M . Рассмотрим движения
т. M на промежутке от t до t t . Тогда S S t t S t , а
скорость. Если существует предел
S
- средняя
t
S
S t ,
t 0 t
lim
то производная от пути по времени есть скорость движения т. M в момент
времени t .
Замечание. Если функция y f (x) описывает некоторый физический
процесс, то производная y f (x) есть с к о р о с т ь п р о т е к а н и я этого
процесса (физический смысл производной).
б) Геометрическая. На кривой y f x
M 0 x0 ; f x0
рассмо-трим
точки
и
Очевидно,
что
M 1 x0 x ; f x0 x .
y
. Будем
x
двигать т. M 1 по кривой к т. M 0 . Фиксируя
M 0 A x, AM 1 y
Рисунок 1
и
tg
ряд промежуточных положений т. M 1 ,
получим секущих M 0 M 1 . Очевидно, что
при M 1 M 0 x 0 (рис. 1).

4.

Определение 3. Если существует предельное положение M 0T секущих M 0 M 1 при
неограниченном приближении т. M 1 по кривой к т. M 0 с любой стороны, то M 0T
называется касательной к кривой y f x в т. x 0 .
Если касательная существует, то
y
f x0 .
x 0 x
tg lim tg lim
x 0
Следовательно, дифференцируемая в т. x 0 функция, имеет в этой точке касательную
с угловым коэффициентом k f x0 .
У р а в н е н и е к а с а т е л ь н о й M 0T к графику функции y f (x) в точке
М 0 х 0 , у 0 имеет вид
y y0 f x0 ( x x0 ) .
Прямая, проходящая через точку касания М 0 х 0 , у 0 перпендикулярно к
касательной, называется н о р м а л ь ю к графику функции y f (x) в этой точке.
Уравнение нормали имеет вид
y y0
1
( x x0 )
f ' ( x0 )

5.

1.2 Правила дифференцирования
Теоремы.
1. Если y f x дифференцируема в т. x 0 , то она непрерывна в этой
точке.
y
y
f x0
f x0 x , где x 0 при x 0 .
Действительно: lim
x 0 x
x
Отсюда y f x0 x x x 0 при x 0 .
2. Производная сложной функции. Если x (t ) дифференцируема в
т. t0 , а y f x - в т. x0 (t0 ) , то сложная функция y F (t ) f [ t ]
дифференцируема в т. t0 и F (t ) f ( x) (t ) , или yt y x xt
3. Правила дифференцирования. Пусть существуют u (x) и v x , а
C - const. Тогда
а) C 0 .
Действительно: f ( x) C f 0 C 0 .
б) u v u v .
в) (uv) u v uv Cu Cu .
u u v uv
г)
.
2
v
v

6.

§ 2. Методы дифференцирования
2.1 Табличное дифференцирование
Пусть u u x , v v x - функции от x , а C , a , - константы. Тогда
7. (arcsin u )
1. xx ' 1
2. u u 1 u
3. sin u cosu u
'
4. (cos u ) sin u u
1
u
2
cos u
1
6. (ctg u ) 2 u
sin u
5. (tg u )
1
u
1 u
1
8. (arccos u )
u
2
1 u
1
9. (arctg u )
u
2
1 u
1
10. (arcctg u )
u
2
1 u
11. (a u ) a u ln a u e u e u u
12. (log u )'
2
1
1
u ln u u
u ln a
u

7.

2.2 Производная обратной функции
Если для функции y f x существует обратная функция x ( y) ,
которая в т. y0 имеет производную, отличную от нуля, то
1
f x0
.
y 0
2.3 Дифференцирование неявной функции F x, y 0
Для нахождения производной по x от неявной функции, необходимо
дифференцировать обе части равенства, считая при этом, что y функция от x .
2.4 Дифференцирование функции, заданных параметрически
Пусть функция y от x задана параметрически
x t
,
t0 t t1 .
y
t
Пусть x t имеет обратную функцию, которая, включая функции t и t ,
дифференцируемы, причем t 0 . Тогда
y x
yt t
xt t

8.

§ 3. Дифференциал функции
y
y
f x
f x , где 0 при
Пусть y f x C1 a ; b . Тогда lim
x 0 x
x
x 0 . Отсюда
y f x x x .
Определение 4. Главная часть приращения функции Δy, линейная относительно Δx,
называется дифференциалом функции и обозначается dy f x x, f ( x) C 1 a ; b .
dy
Пусть y x . Тогда dy dx x dy f x dx f x dx .
Отметим следующие свойства дифференциала функции:
1. d u v du dv
2. d u v udv vdu
3. d uv vdu 2 udv
v
4. Пусть y f u , u x или y f x . Тогда
dy
f u x dy f u x dx f u u du dx
дифференциала.
свойство инвариантности формы

9.

5. Так как при f x 0 .
y
y
1 lim
1,
dy
f x x 0 dy
то в приближенных вычислениях можно считать y dy , или
f x x f x x f x
Пример. Вычислить y 4,001 .
Рассмотрим функцию y x и т. x 4 . За x x возьмем 4,001 .
Тогда x 0,001, f 4 2 .
f x 1 f 4 1 0,25 . Тогда из (2)
2 x
2 4
f 4,001 0,25 0,001 2 2,0025 .
(2)

10.

§ 4. Производные и дифференциалы высших порядков
Пусть y f x C1 a ; b . Если z f x C1 a ; b , то z называется второй
производной от y f x и обозначается f x . Т. е.
y x y x
Определение 5. Производной от функции y f x n -го порядка называется
производная от производной n 1 -го порядка, т.е.
f n x f n 1 x
f x f x или
Замечание. Если известен закон прямолинейного движения материальной
точки в виде S S t , тогда известно, что скорость V S t ,
а ускорение движения a V t S t .
Пусть функция y f (x) задана параметрически
x x(t )
,
где t – параметр.
y
y
(
t
)
Известно, что первая производная находится по формуле:
y t
yx
,
x t

11.

тогда производная второго порядка имеет вид
'
y t
'
y х t xt t
y хх
x t
x t
Пусть dy f x C1 a ; b . Тогда d 2 y d dy называется дифференциалом
второго порядка от f x . Отсюда
2
d 2 y d dy f x dx dx f x dx f x dx2 .
Определение 6. Дифференциалом n -го порядка функции y f x называется
дифференциал от дифференциала n 1 -го порядка, причем
d n y f n x dxn
(3)
Из (3) следует
dny
f x n
dx
n
(4)