Похожие презентации:
Дифференциальное исчисление функции одной переменной (производная)
1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ (производная)
2. Производная функции, её геометрический и механический смысл
3.
Пусть функция y = f(x)определена в некоторой
окрестности точки х. Если
переменная х получит
приращение Δx, то функция у
получит приращение
Δy = f(x + Δx) – f(x).
4.
Определение. Производнойфункции y = f(x) в точке х
называется предел отношения
приращения функции Δy к
приращению аргумента Δx,
когда Δx→0, т.е.
y
f ( x x) f ( x)
y lim
lim
x
x 0 x x 0
5.
Для производной функцииy = f(x) в точке х применяют
также обозначения:
dy df (x)
f (x)
dx
dx
Функция, имеющая в данной
точке конечную производную,
называется дифференцируемой
в этой точке.
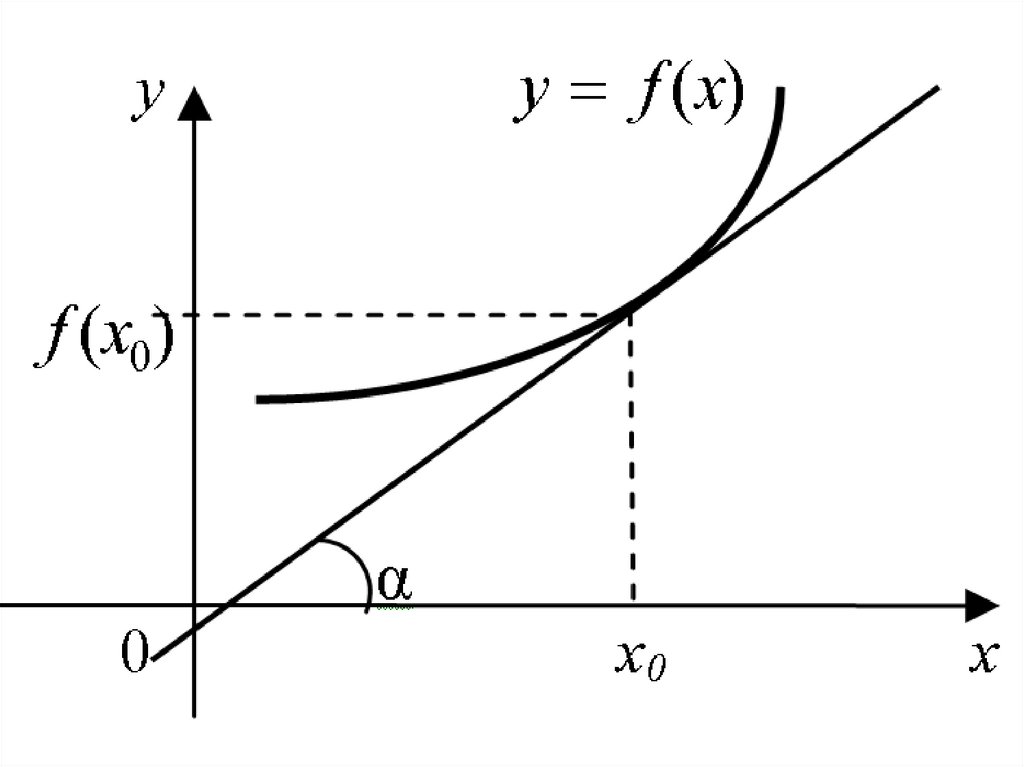
6. Геометрический смысл производной
Построим график функцииy = f(x) и проведём к нему
касательную через точку
M(x0, f(x0)).
7.
8.
Обозначим через α угол,образованный этой касательной
c осью Ox, тогда
tg f (x0)
9.
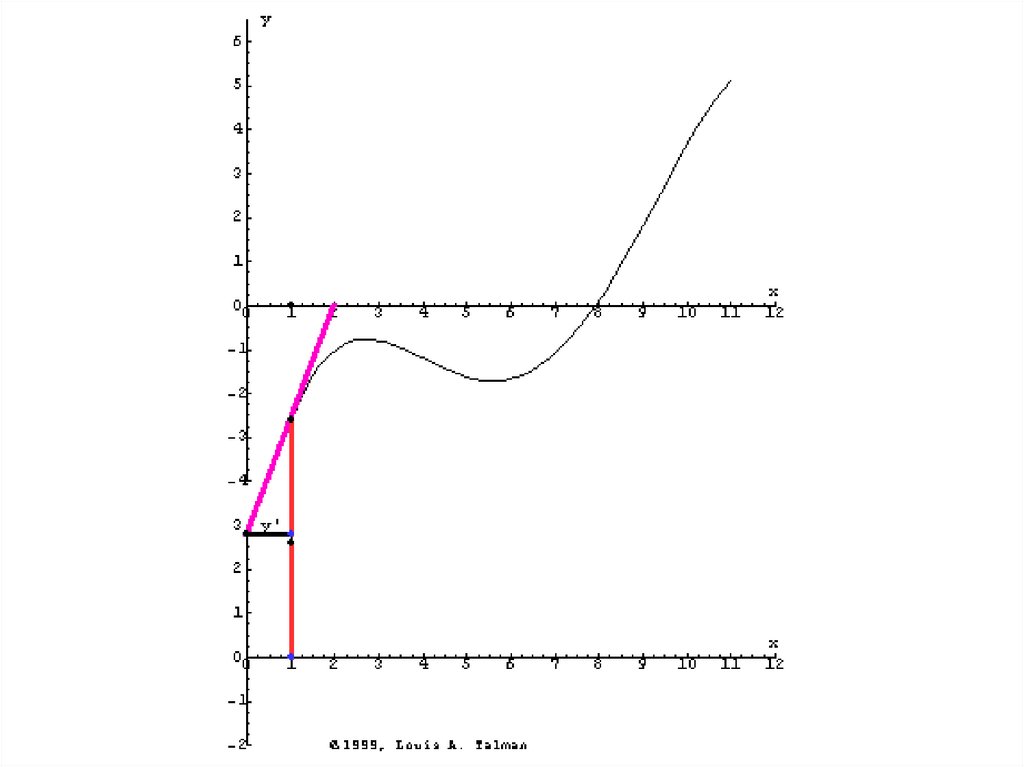
т.е. производнаяфункции y = f(x)
равна угловому
коэффициенту
касательной к
графику этой
функции в точке с
абсциссой x0.
10.
11.
Уравнениекасательной к
кривой y = f(x) в
точке M(x0, f(x0)) имеет
вид
y f (x0) f (x0)(x x0)
12.
а уравнениенормали к данной
кривой в точке M(x0,
f(x0)) записывается
1
в
виде
:
y f (x0)
(x x0)
f (x0)
при условии, что
13.
Если f′(x0) = 0, тоуравнение
касательной: y = f(x0),
уравнение
нормали: x = x0.
14. Механический смысл производной
Пустьматериальная
точка движется
прямолинейно по
закону s = s(t). Тогда
v = s′(t), т.е.
15. Основные правила дифференцирования
Основныеправила
дифференцирова
ния
Если функции u и v
дифференцируемы,
то
16.
• 1.(cu ) cu , c const
• 2.
(u v) u v
• 3.
(u v) u v u v
u
u
v
u
v
• 4.
,
v
0
2
v
v
17.
• 5. Если y = f(u) и u = φ(x) –дифференцируемы
е функции своих
аргументов, то
сложная функция
y = f(φ(x))
тоже
y x
yu u x
дифференцируема
и
dy dy du
dx du dx
18.
Это правилолегко
распространить
на цепочку из
любого конечного
числа
дифференцируемы
х функций.
19.
• 6. Если длядифференцируемо
й функции y = f(x)
(f′(x) ≠ 0) существует
1
(
y
)
обратная функция
f ( x)
x = φ(y), то
1
x y
y x
или
20.
• 7. Если функциязадана
параметрически
x x (t ),
уравнениями
y y (t ),
то ее
y
t
y
(t )
производная
y x
y ( x)
вычисляется
по
x
x (t )
t
21. Производные некоторых элементарных функций
22.
y x2
y ( x x) x
2
2
x 2 x x ( x)
2
2 x x ( x)
2
2
23.
y2 x x ( x)
y lim
lim
x 0 x
x 0
x
lim (2 x x) 2 x
2
x 0
( x ) 2 x
2
24.
y sin xy sin( x x) sin x
x x x
x x x
2 sin
cos
2
2
x
x
2 sin cos(x )
2
2
25.
y(sin x) lim
x 0 x
x
2 sin
x
2
lim
lim cos x
x 0
x 0
x
2
2
1 cos x cos x
26.
y tg xsin x
(tg x)
cos x
sin x cos x sin x cos x
2
cos x
cos x cos x sin x sin x
2
cos x
27.
cos x sin x1
2
2
cos x
cos x
2
(tg x)
2
1
2
cos x
28. Производная обратной функции
Пусть требуетсянайти
производную
функции у = f(x) при
условии, что
обратная ей
29.
Для решения этойзадачи
дифференцируем
функцию
x = g(y) по
х:
1 g ( y ) y
1
т.к. g (y) 0, то
y
g ( y )
30.
dy1
dx dx
dy
т.е. производная
обратной функции
обратна по
31.
• Пример. Найтиформулу для
производной
функции arctg x.
32.
Решение. Функцияarctg x является
функцией,
обратной функции
tg x:
y tgx;
x arctgy;
33.
Известно, что1
y (tgx)
;
2
cos x
По формуле
производной
обратной
1 функции
y
;
получаем:
d (arctgy) / dx
d (arctgy)
1
2
dy
1 / cos x
34.
Т.к.1
2
2
1
tg
x
1
y
;
2
cos x
то можно
записать
окончательную
формулу для1
производной
(arctgy)
2
1 :y
арктангенса






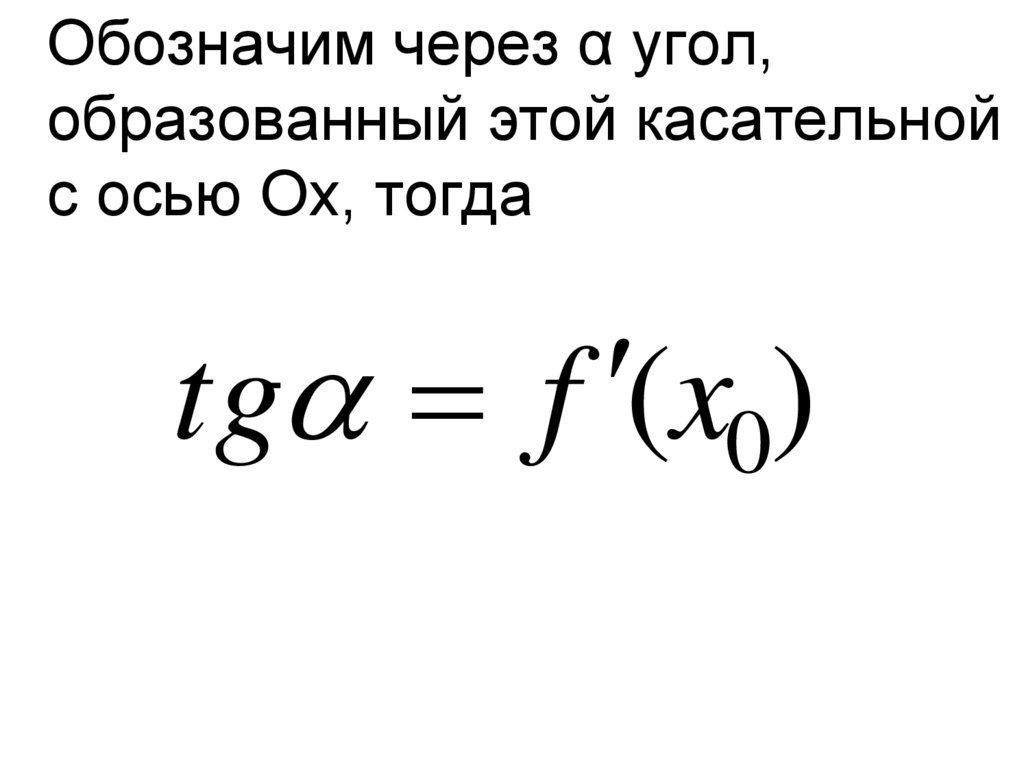

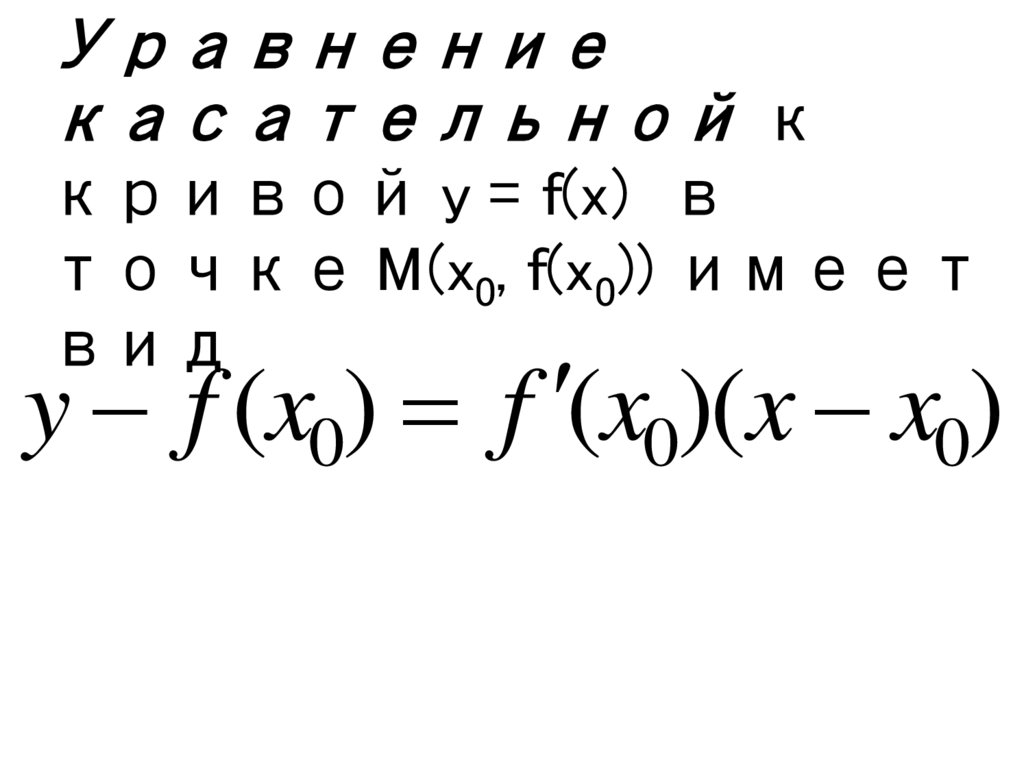
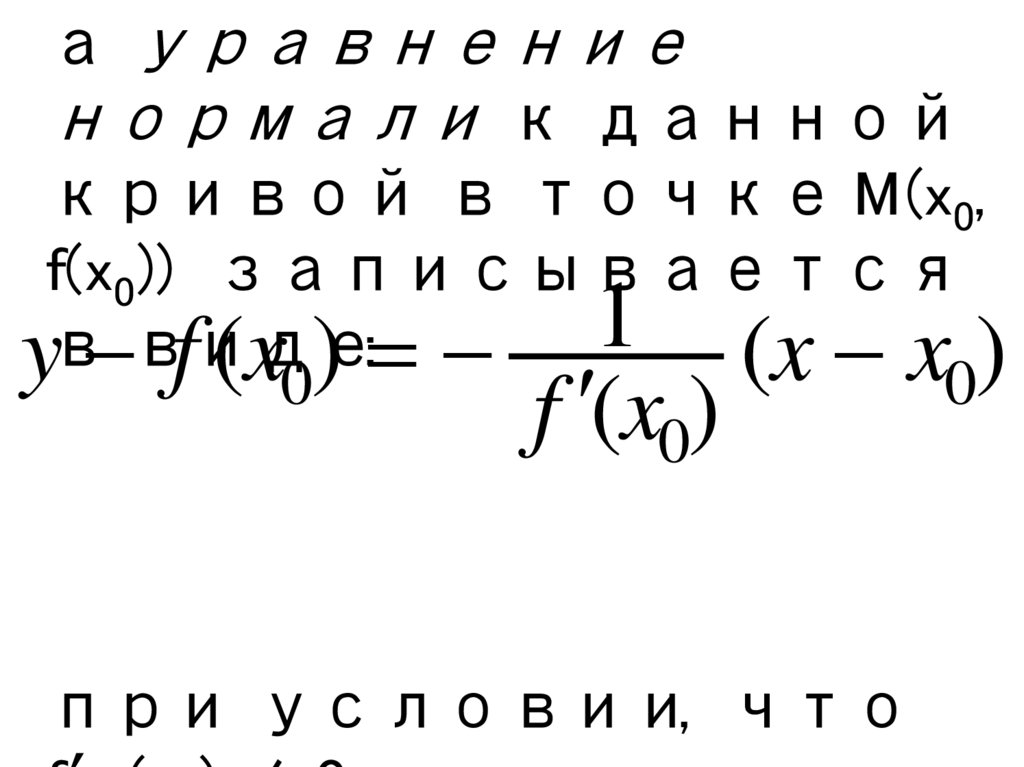
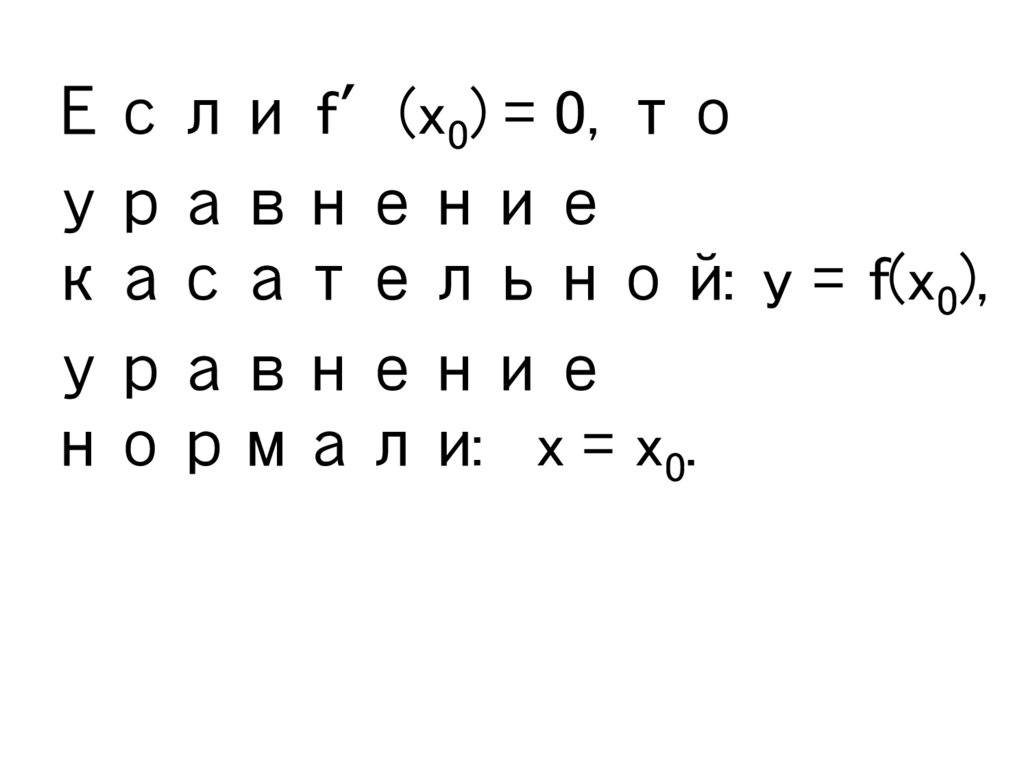


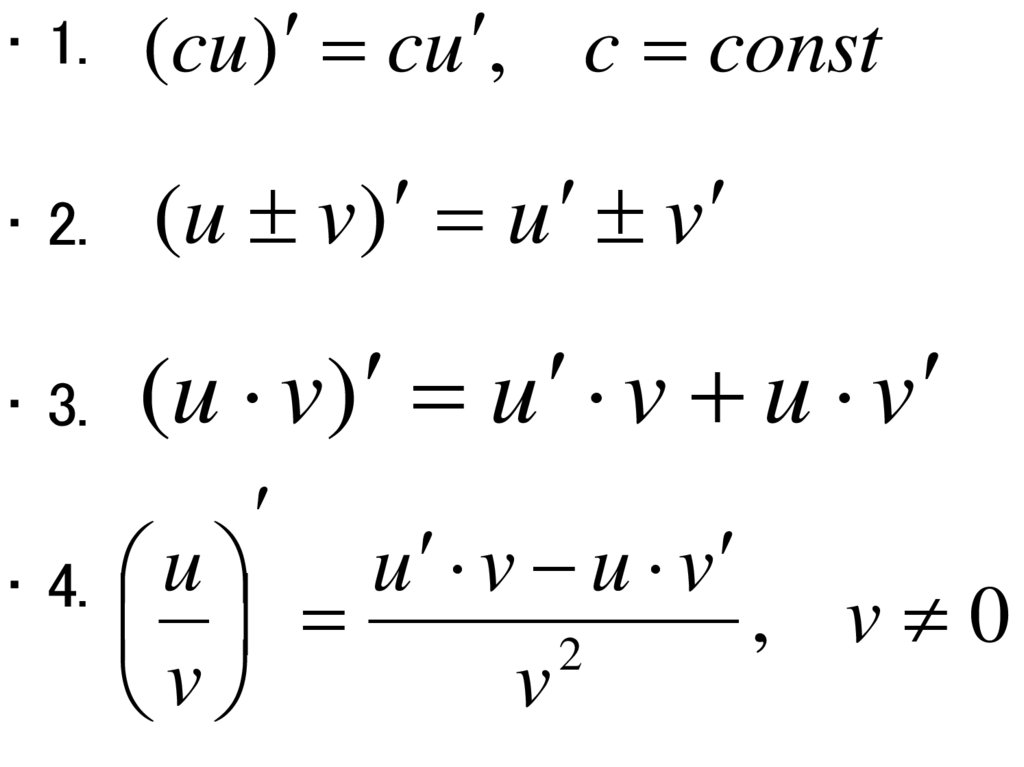
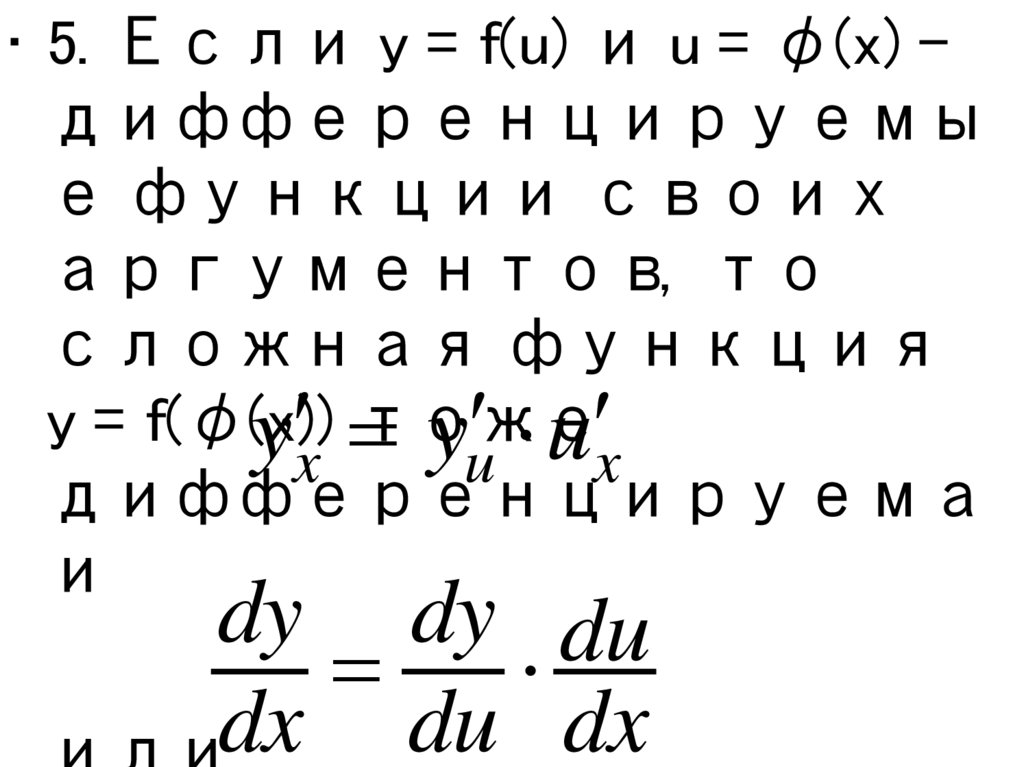


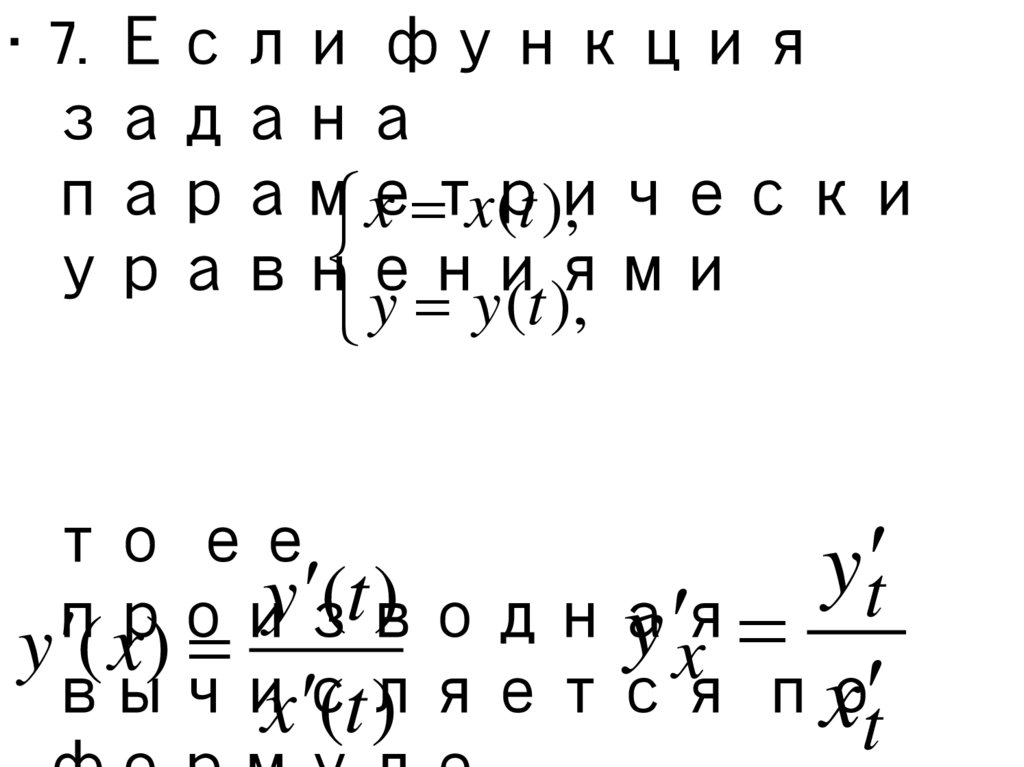

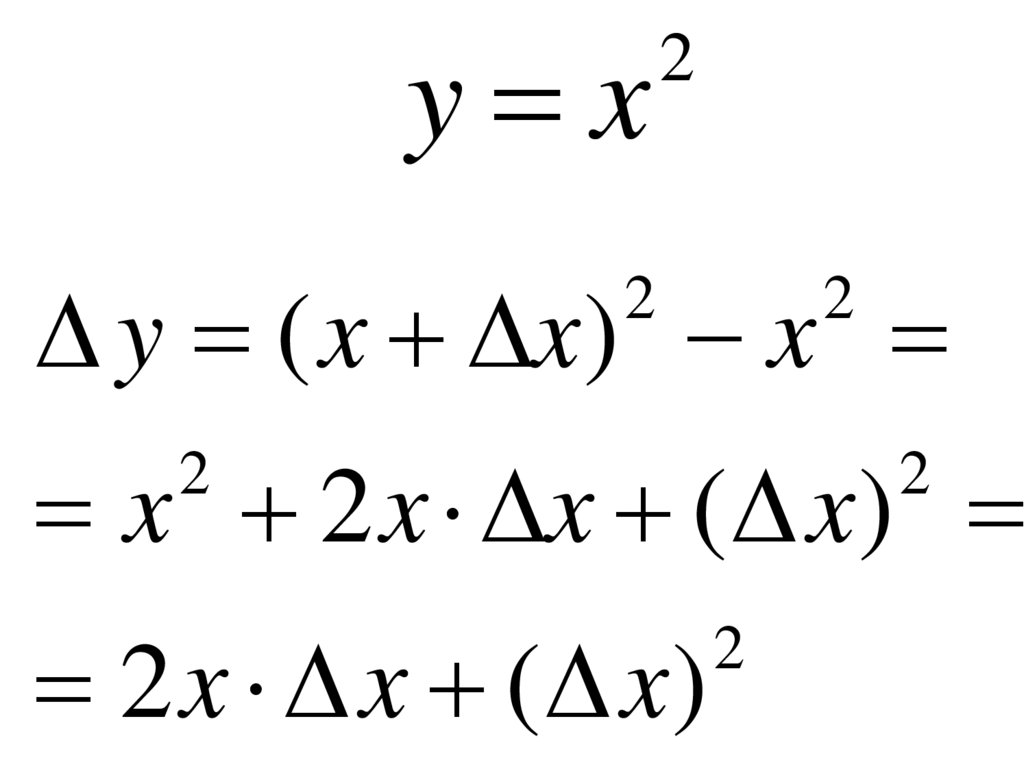
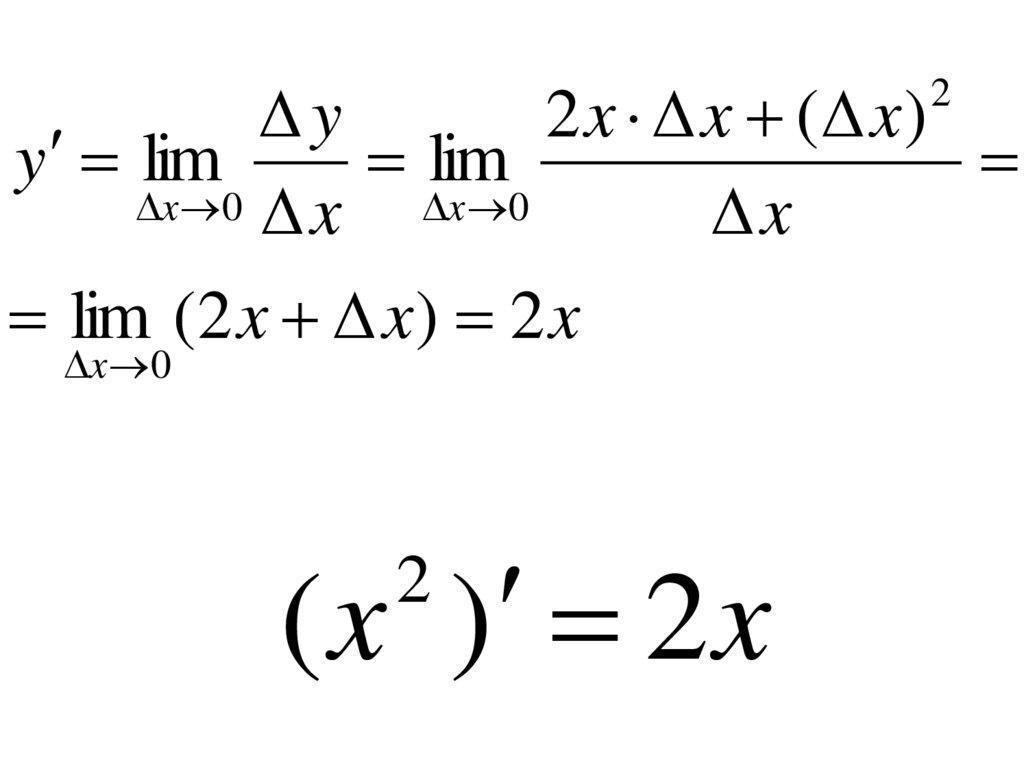
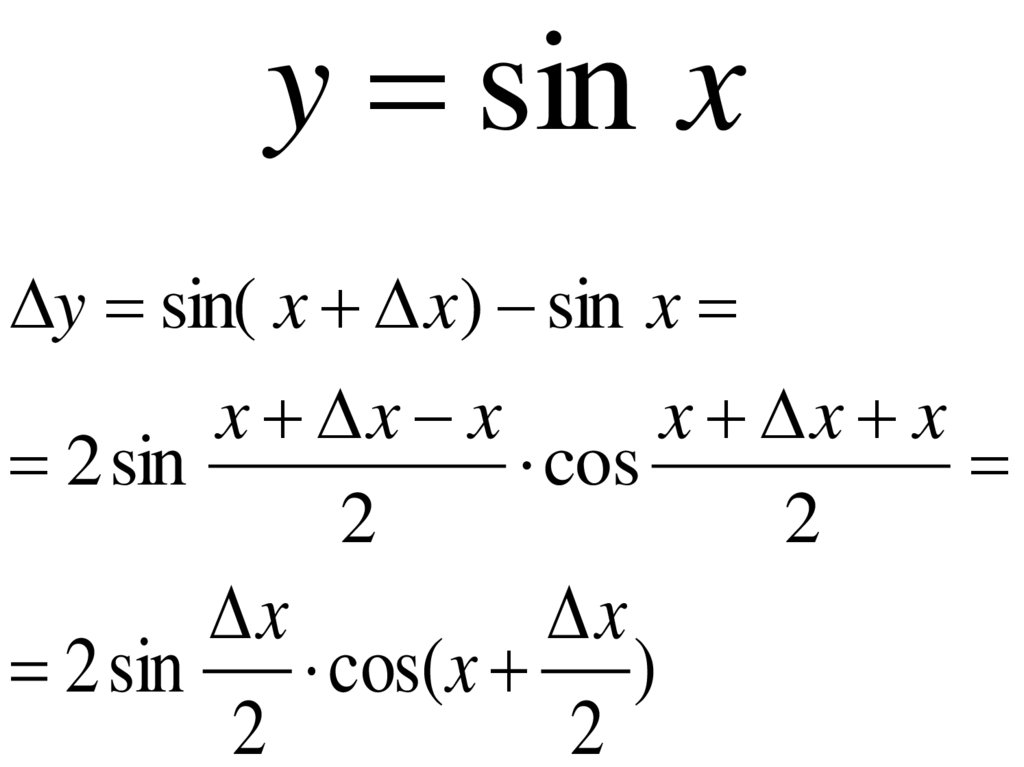
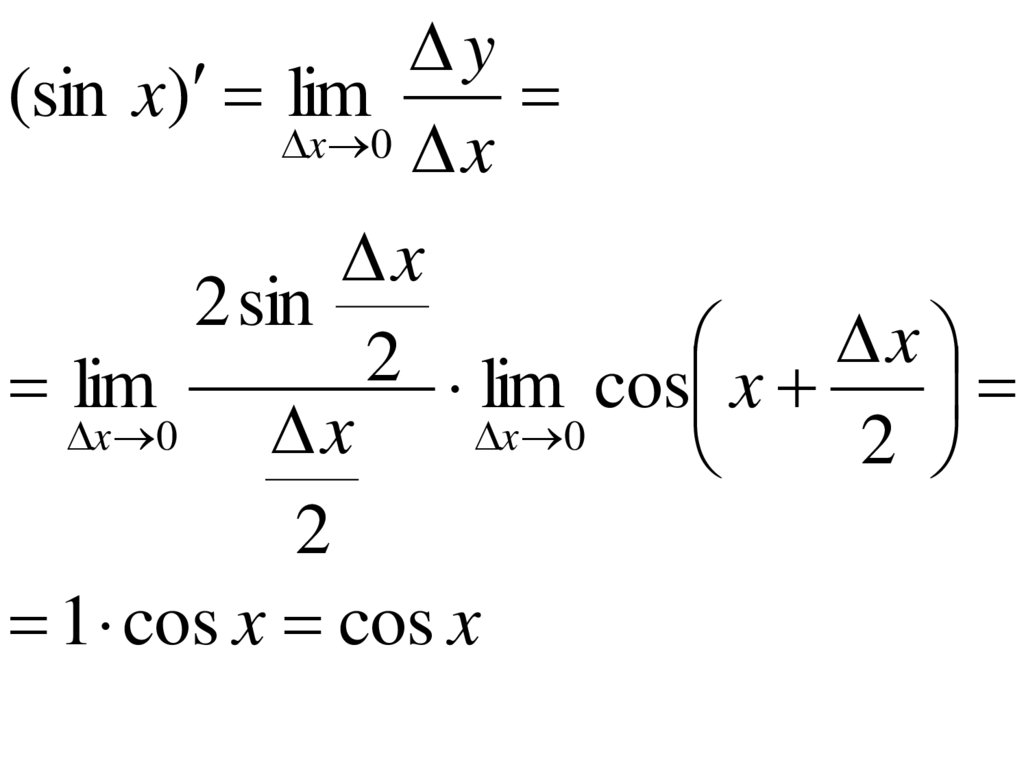
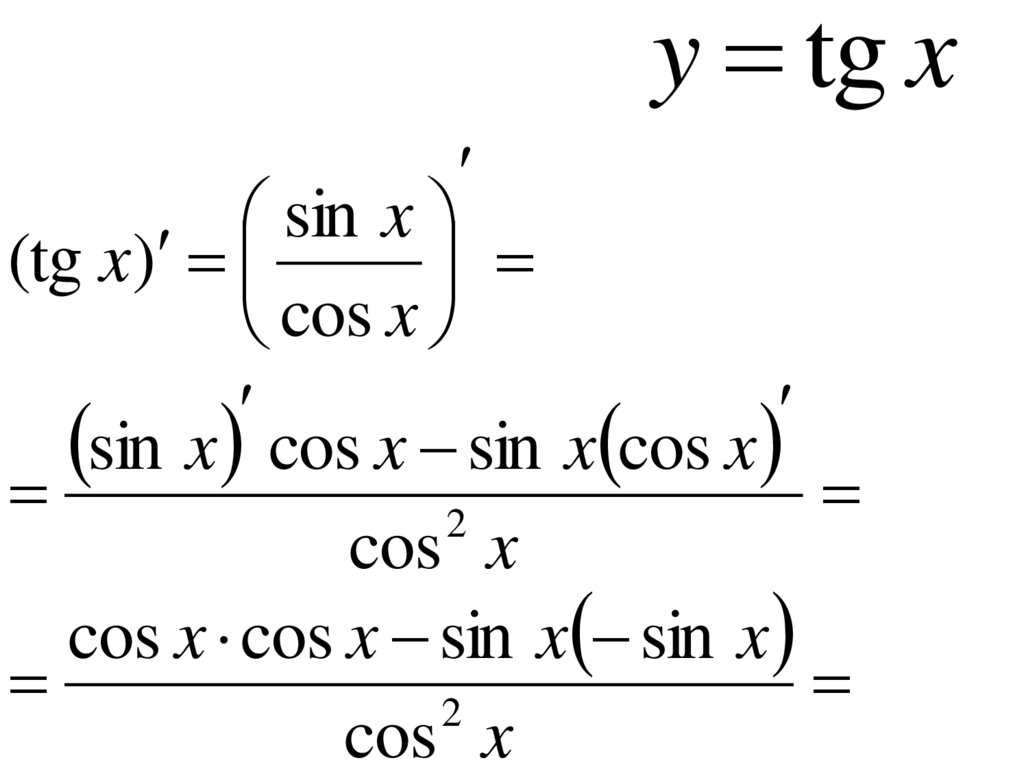
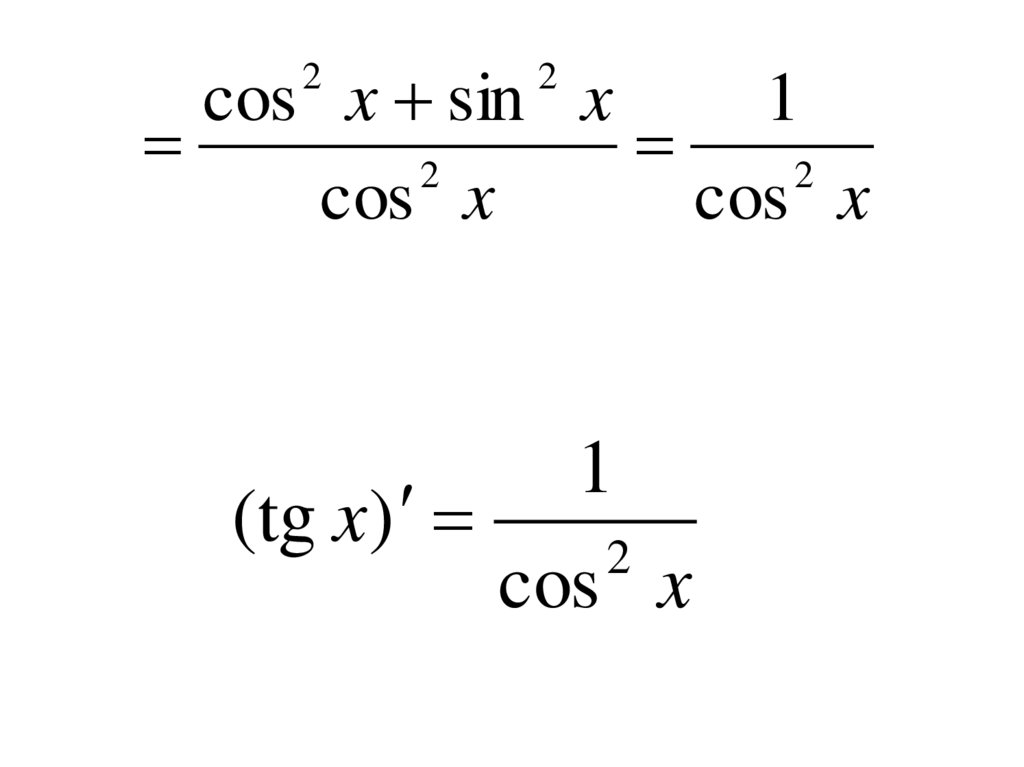

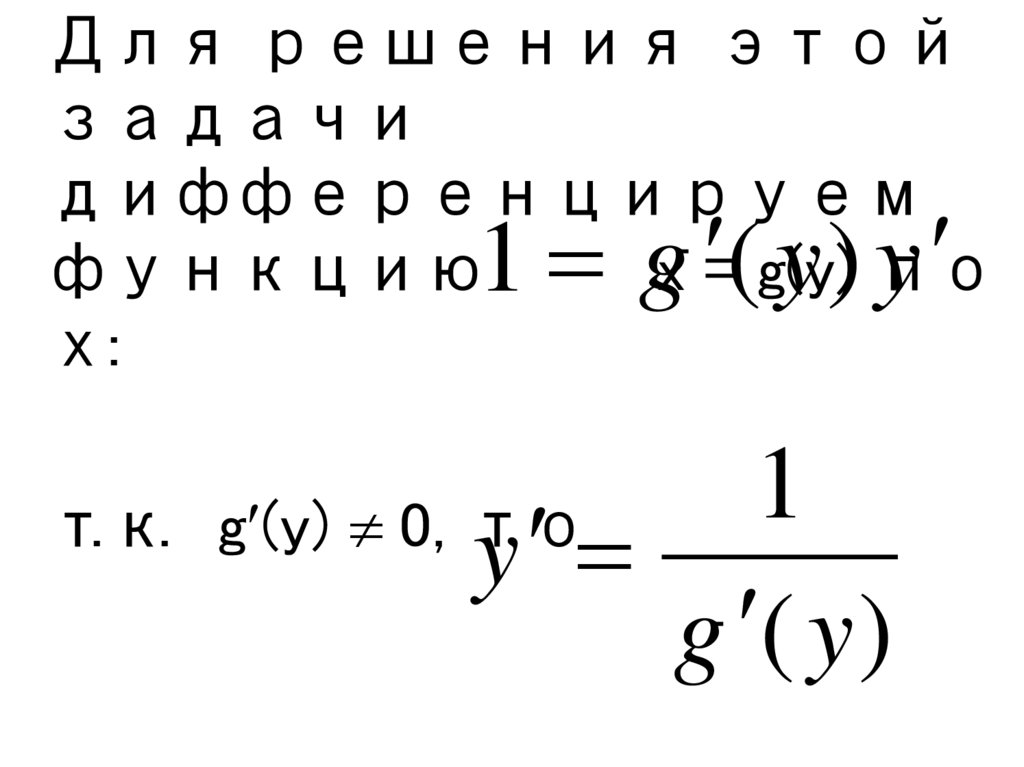
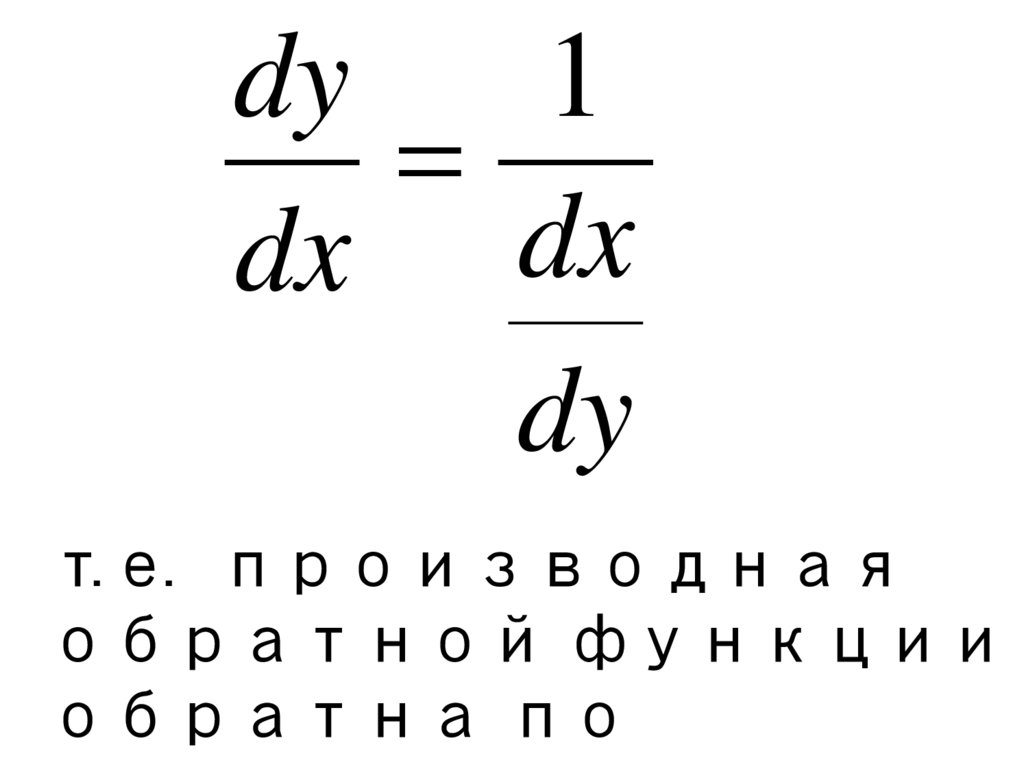

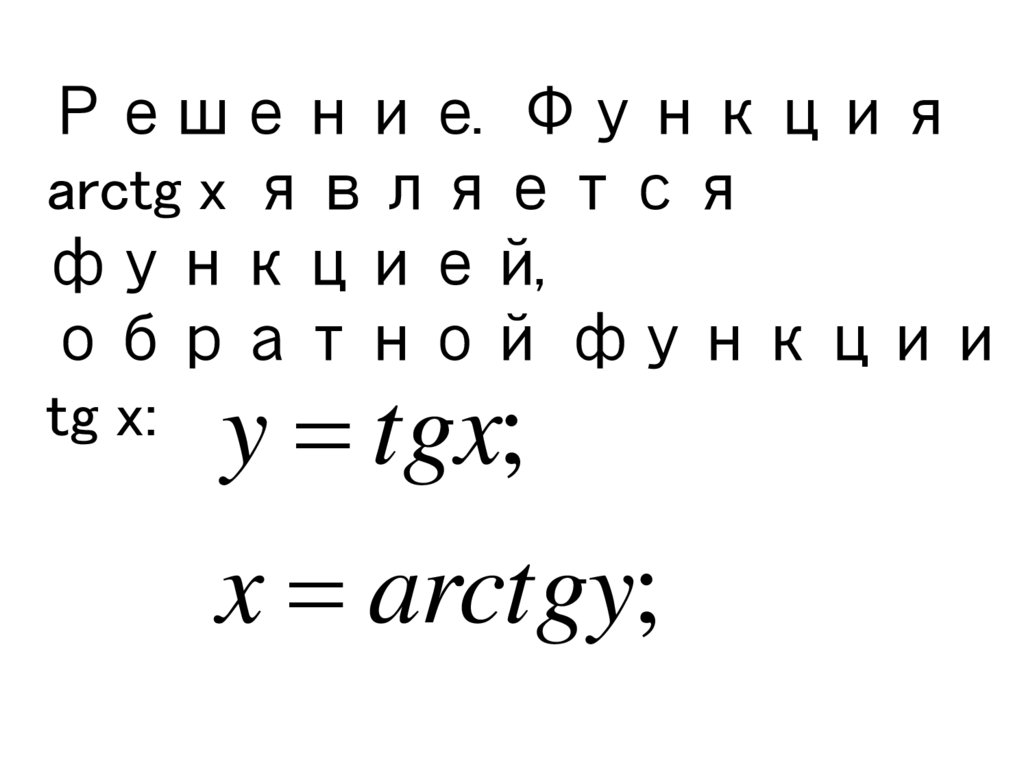
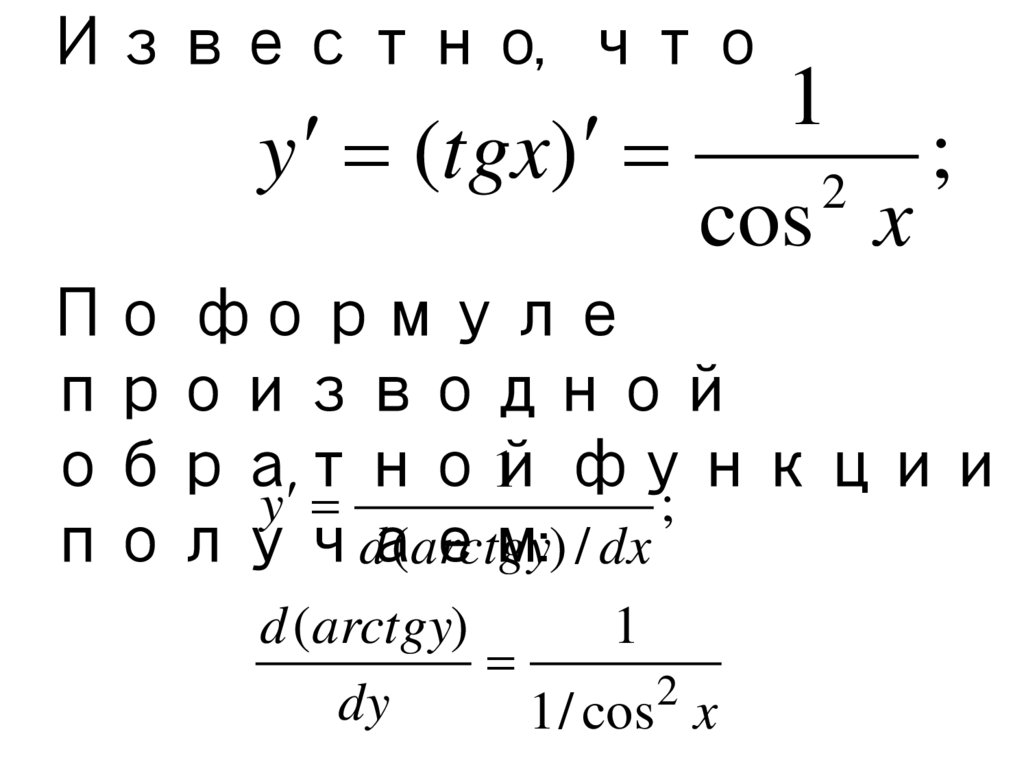
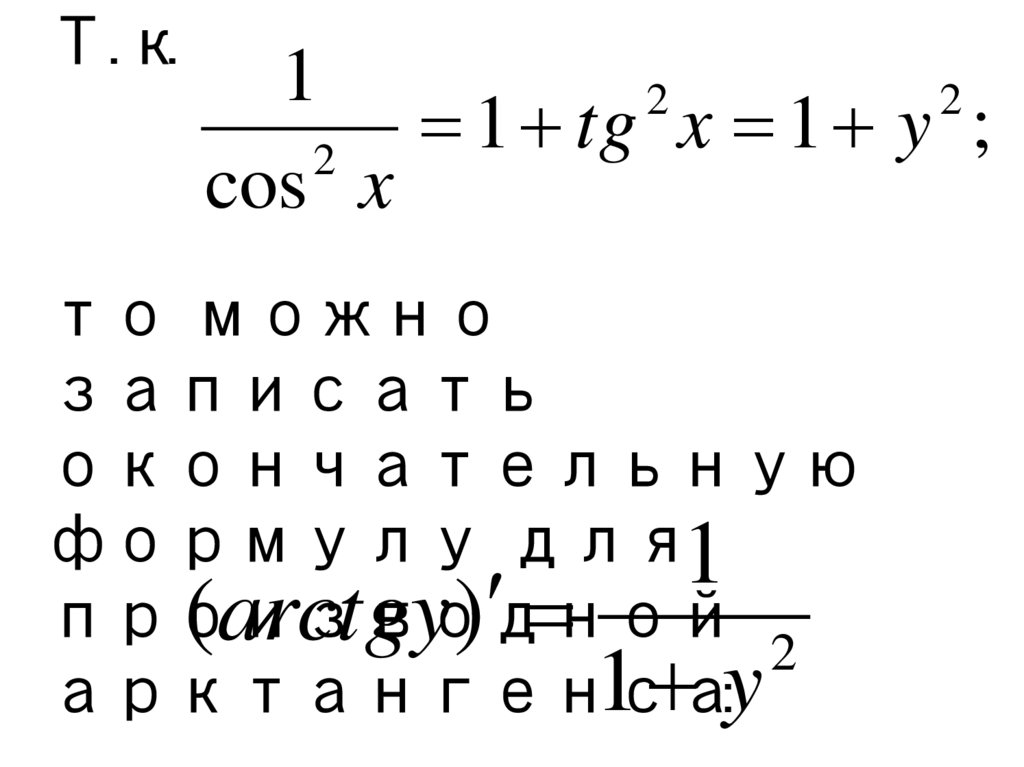
 Математика
Математика








