Анализ рядов динамики

1. Анализ рядов динамики

Изучение изменений общественных явлений во
времени производится при помощи анализа
рядов динамики (временных рядов).
Динамический ряд распределения (ряд
динамики) —числовые значения
статистического показателя, представленные
во временнóй последовательности (т.е.
расположенные в хронологическом порядке).

2.

Он состоит из двух элементов:
- периода времени, за который или по состоянию на
который приводятся числовые значения;
- числовых значений того или иного показателя,
которые и называют уровнями ряда.
Уровни ряда обычно обозначаются через «у»,
моменты или периоды времени – через «t».
Первый член ряда y0 (или у1) называют начальным
уровнем, а последний yn – конечным
Ряд динамики можно изобразить графически или
представить в табличной форме

3. Ряды динамики могут быть классифицированы по следующим признакам:

• В зависимости от способа выражения уровней
ряда динамики: ряды абсолютных,
относительных и средних величин.
• В зависимости от характера отображения
времени: моментные и интервальные.
• В зависимости от величины интервалов между
периодами или моментами времени: с
равными и с неравными промежутками
времени

4.

Этапы анализа динамического ряда
распределения :
1) определение сопоставимости уровней ряда
динамики;
2) анализ интенсивности изменения уровней
ряда динамики;
3) выявление тенденции в развитии изучаемого
явления;
4) выявление и измерение сезонных колебаний
в ряду;
5) прогнозирование развития явления
(показателя) на будущее.

5.

1. Определение сопоставимости уровней
динамического ряда.
Для проведения анализа динамического ряда
необходимо, чтобы все его уровни были
сопоставимы во времени и в пространстве.
Несопоставимость статистических рядов динамики
может быть вызвана:
• изменением границ территории;
• изменением даты учета;
• изменением методологии расчета показателей;
• изменением цен;
• различной продолжительностью периодов.

6.

Если уровни ряда динамики несопоставимы,
их необходимо привести к сопоставимому
виду и построить новый динамический ряд:
1) необходимо знать значение
анализируемого показателя в новых
условиях (или границах) и в старых.
Для этого необходимо, чтобы в год
изменения методологии расчета (например,
из-за изменения территориальных границ)
один и тот же уровень ряда приводился в
двойной оценке: по прежней и новой
методике (в старых и новых границах)

7.

2) рассчитать коэффициент смыкания
(пересчета):
где yнов— значение уровня ряда в новых
условиях (границах); yстар—значение уровня
ряда в старых условиях(границах).
3) все значения показателя в старых границах
умножить на полученный коэффициент
4) новый динамический ряд считается
сопоставимым и его можно анализировать.

8.

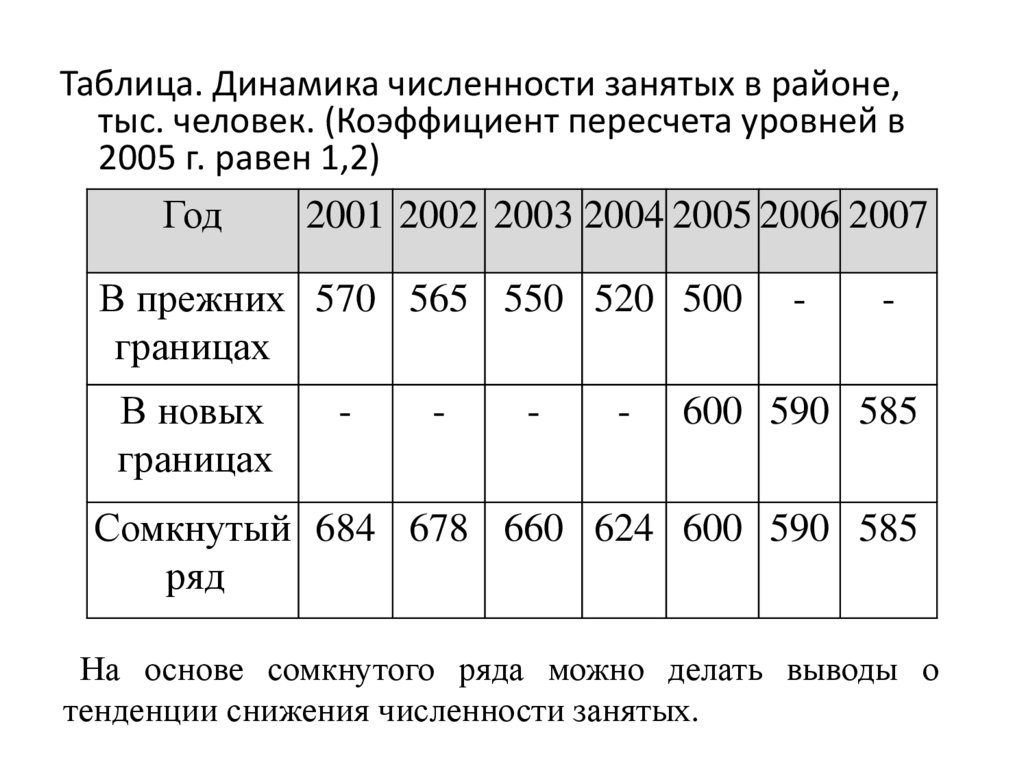
Пример. В 2005 г. были изменены границы
административного района и численность
занятых в экономике составила в прежних
границах 500 тыс. человек, а в новых
границах 600 тыс. человек.
Коэффициент пересчета уровней в 2005 г.
равен 1,2 (600/500).
Умножая на этот коэффициент уровни ряда
динамики в прежних границах, приводим
их к сопоставимому виду

9.

Таблица. Динамика численности занятых в районе,
тыс. человек. (Коэффициент пересчета уровней в
2005 г. равен 1,2)
Год
2001 2002 2003 2004 2005 2006 2007
В прежних 570 565 550 520 500
границах
В новых
границах
-
-
-
-
-
-
600 590 585
Сомкнутый 684 678 660 624 600 590 585
ряд
На основе сомкнутого ряда можно делать выводы о
тенденции снижения численности занятых.

10. Сопоставление нескольких взаимосвязанных рядов динамики:

Особое внимание надо обращать на сопоставимость
уровней интервальных и моментных рядов
динамики.
Например, сравниваются за ряд лет прибыль
предприятия (интервальный ряд) и стоимость
основных производственных фондов на конец года
(моментный ряд) эффективность использования
основных производственных фондов.
Чтобы сопоставление было возможно, необходимо
уровни моментного динамического ряда пересчитать
в среднегодовые уровни в этом случае и прибыль,
и основные фонды будут отражать годовые значения

11.

2. Определение интенсивности изменения уровней
динамического ряда.
Для оценки интенсивности изменения уровней ряда во
времени рассчитываются:
• абсолютные,
• относительные и
• средние показатели ряда динамики.
При анализе динамического ряда приняты следующие
обозначения:
yi — текущее значение уровня ряда;
yi−1— предыдущее значение уровня ряда;
y1 — начальный уровень ряда;
yn— конечный уровень ряда.

12.

2.1. Абсолютные и относительные
показатели можно рассчитывать:
• с постоянной базой сравнения - текущий
уровень показателя сравнивается с
начальным уровнем или каким-то другим,
принятым за базу сравнения (показатель
называется базисным),
• с переменной базой сравнения - текущий
уровень показателя сравнивается с
предыдущим уровнем (показатель
называется цепным).

13.

2.1.1. Абсолютный прирост - показывает, на
сколько в абсолютном выражении текущее
значение показателя больше или меньше
уровня, принятого за базу сравнения.
Он равен разности двух сравниваемых уровней :
• цепной прирост:
∆yiц = yi− yi−1;
Абсолютный прирост с переменной базой
называют скоростью роста.
• базисный прирост:
∆yiб = yi− y1.

14.

• Если значения цепных абсолютных
приростов (изменений) постоянны, то
уровни ряда изменяются равномерно.
• Если же абсолютные приросты от периода к
периоду возрастают (или убывают), то
уровни изменяются ускоренно (или
замедленно).
• В этом случае можно рассчитать
показатель ускорения как разность между
двумя смежными цепными абсолютными
приростами: = i - i-1

15.

16.

Кр Кр
б
ц
i
16

17.

2.1.3. Темп роста показывает, сколько процентов
уровень текущего периода составляет относительно
уровня, взятого за базу сравнения
• Темп роста (цепной)
yi
Тр
100%
yi 1
ц
• Темп роста (базисный)
• Темп роста = Коэффициент роста * 100%
17

18.

19.

20.

21.

2.1.6. Относительное ускорение –
разность следующих друг за другом:
- темпов роста:
ц
ц
i 1
Трi Тр
''
- темпов прироста:
ц
ц
i 1
Трi Тр
'''
2.1.7. Коэффициент опережения –
отношение текущего темпа роста к предыдущему:
ц
Трi
Копрережения
ц
Трi 1
21

22. 2.2. Средние показатели в рядах динамики

Для обобщения данных по рядам динамики
рассчитывают:
• средний уровень ряда динамики,
• средний абсолютный прирост,
• средние темпы роста и прироста

23.

2.2.1. Показатели среднего уровня ряда динамики
а) Средний уровень интервального ряда динамики
определяется по формуле средней арифметической:
при равных интервалах - средняя арифметическая
простая:
y
y y ... y
y
i
n
1
2
n
n
23

24.

при неравных интервалах - средняя
арифметическая взвешенная:
y t
y
t
i
i
i
где y i - уровни ряда динамики, сохраняющиеся без
изменения в течение промежутка времени t
t i - веса, длительность интервалов времени (дней,
месяцев) между смежными датами.
24

25.

б) Средний уровень моментного ряда
определяется по формуле средней
хронологической
с равными промежутками
y1
yn
y2 y3 ... yn 1
2
y 2
n 1

26. Логика формулы

27.

с неравными промежутками
y
( y1 y2 ) t1 ( y2 y3 ) t2 ... ( yn 1 yn ) tn 1
2 (t1 t2 ... tn 1 )
где ti – интервал времени между смежными
рядами

28. Логика формулы

29.

Пример. Расчет среднего уровня моментного ряда динамики с равноотстоящими
уровнями по данным на 1-е число каждого месяца 2010 г.:
1 января
1 февраля
1 марта
1апреля
Среднемесячная численность работников фирмы за I
квартал составит:
347
350
349
351
Пример. Известна списочная численность рабочих промышленной организации на
некоторые даты (человек). Ряд динамики имеет неравноотстоящие уровни во времени:
1 января 2010 г.
1 марта 2010 г.
1 июня 2010 г.
1 сентября 2010 г.
1 января 2011 г.
530
570
520
430
550
Среднемесячная численность работников фирмы за
год составит:

30.

• Если же предполагается, что каждое
значение уi остается неизменным до
следующего (i + 1)-го момента, т.е. известна
точная дата изменения уровней, то расчет
можно осуществлять по формуле
y t
y
t
i
i
i
• где ti — время, в течение которого уровень
уi оставался неизменным.

31.

2.2.2. Средний абсолютный прирост за весь период
– показывает, на сколько в среднем за единицу времени в
абсолютном выражении текущий уровень больше или меньше
предыдущего,
– другими словами это прирост (уменьшение) в единицу
времени.
Для его определения используют формулу простой средней
арифметической:
–
Более удобная формула среднего абсолютного прироста:
где yn, y1 — конечный и начальный уровни ряда динамики
соответственно.

32.

3.2.3. Средние темпы роста и прироста
а) Средний коэффициент роста – показывает,
во сколько раз в среднем за единицу
времени текущий уровень больше или
меньше предыдущего
Где m – число коэффициентов

33.

б) средний темп роста - показывает, сколько
процентов в среднем за единицу времени
текущий уровень составляет относительно
предыдущего:

34.

в) Средний темп прироста -показывает, на сколько
процентов в среднем за единицу времени текущий
уровень больше или меньше предыдущего.
Не может быть определен непосредственно на
основании последовательных темпов прироста. Для
его вычисления необходимо:
• сначала найти средний темп роста,
• а затем уменьшить его на единицу или на 100%:

35.

3. Выявление тенденции в развитии
изучаемого явления
Уровень динамического ряда можно рассматривать
как функцию трех компонент:
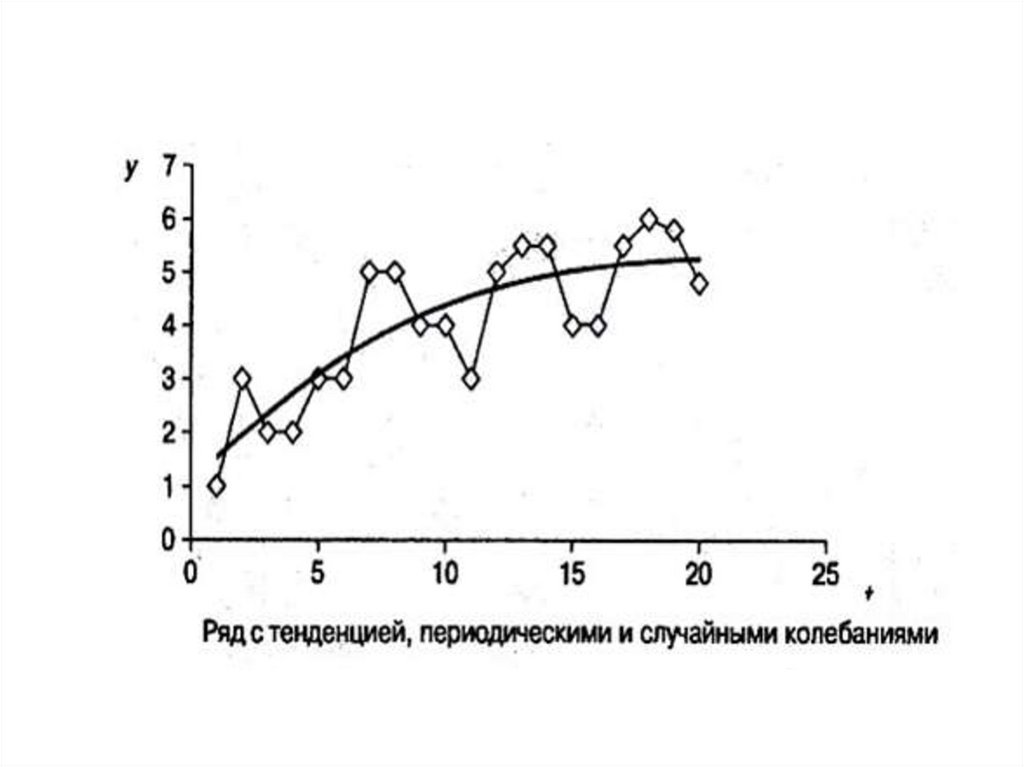
• тенденции ряда, характеризующей основное
направление развития явления за длительный
период времени, т. е. тренд ряда (T);
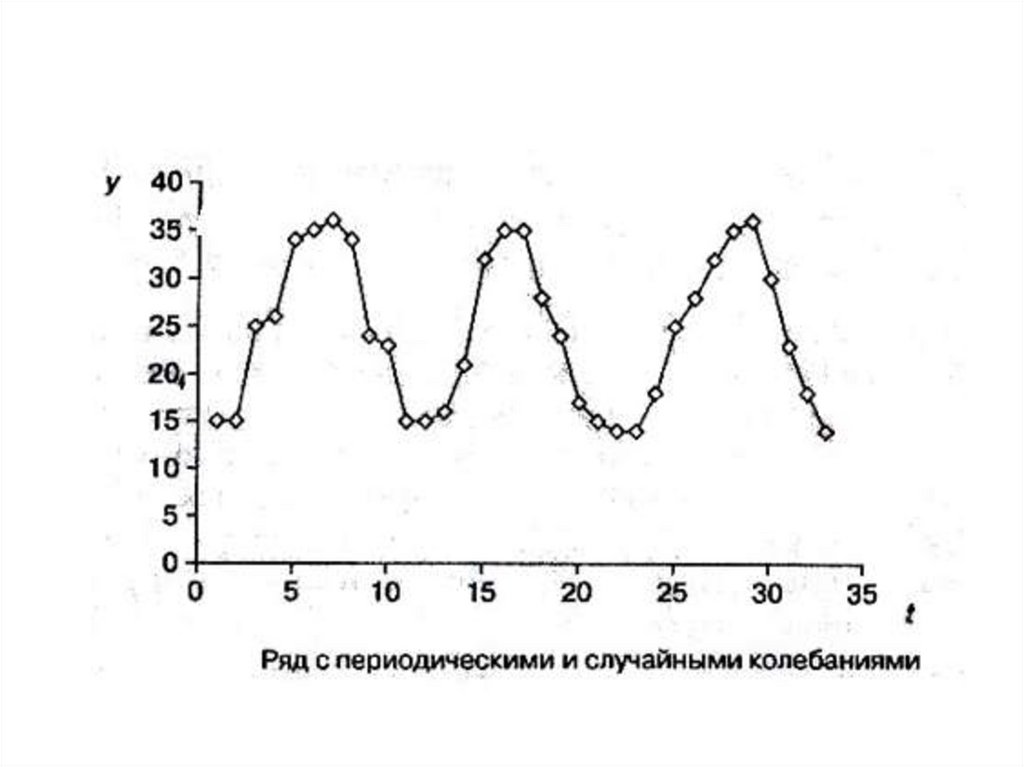
• периодических колебаний, вызванных
особенностями существования явления в одни
периоды по сравнению с другими (Р)
• случайных колебаний, связанных с действием
разного рода второстепенных факторов (Е).

36.

Связь этих компонент с уровнем ряда
представляют в виде аддитивной или
мультипликативной модели:
• yt = Т+ Р + Е — аддитивная модель;
• yt = Т Р Е — мультипликативная модель.

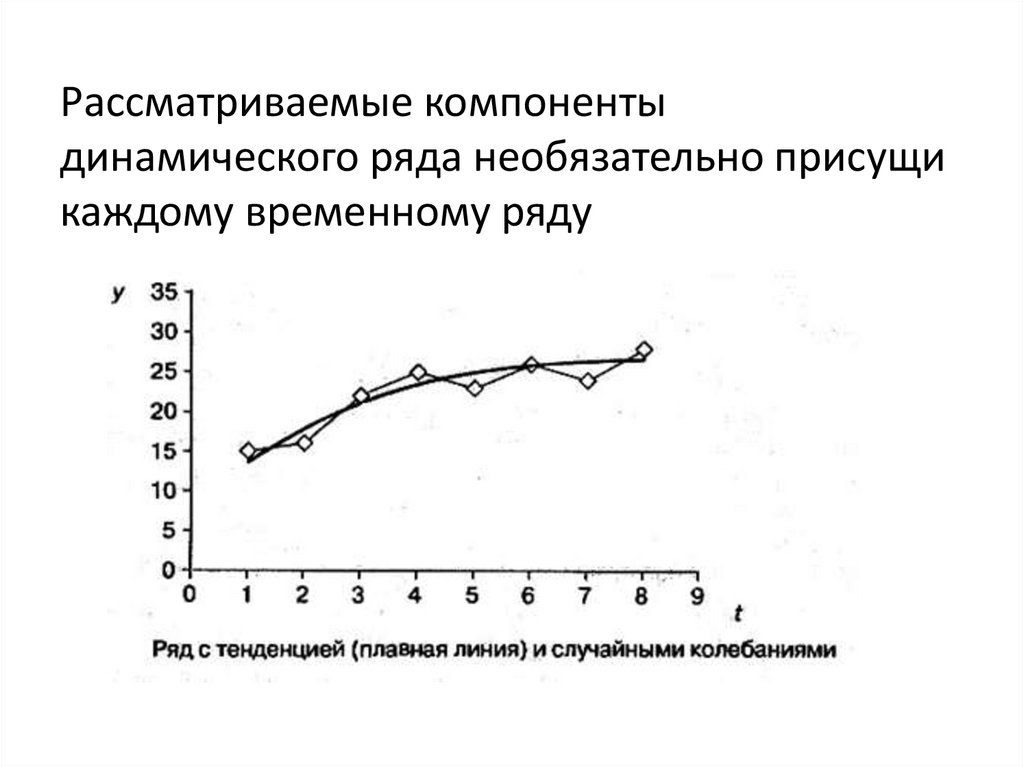
37.

Рассматриваемые компоненты
динамического ряда необязательно присущи
каждому временному ряду

38.

39.

40.

3.1. Основная тенденция развития (тренд) –
плавное и устойчивое изменение уровня
явления во времени, свободное от случайных
колебаний.
Задача - выявить общую тенденцию в
изменении уровней ряда, освобожденную от
действия случайных факторов.

41.

1) Метод укрупнения интервалов - основан
на укрупнении периодов времени, к которым
относятся уровни ряда динамики
(одновременно уменьшается количество
интервалов).
Суточные данные заменяют пятидневными,
декадными, месячными; месячные —
квартальными, годовыми; годовые — трехпятилетними.
Чем меньше период, за который приводятся
данные, тем больше влияние случайных факторов.

42.

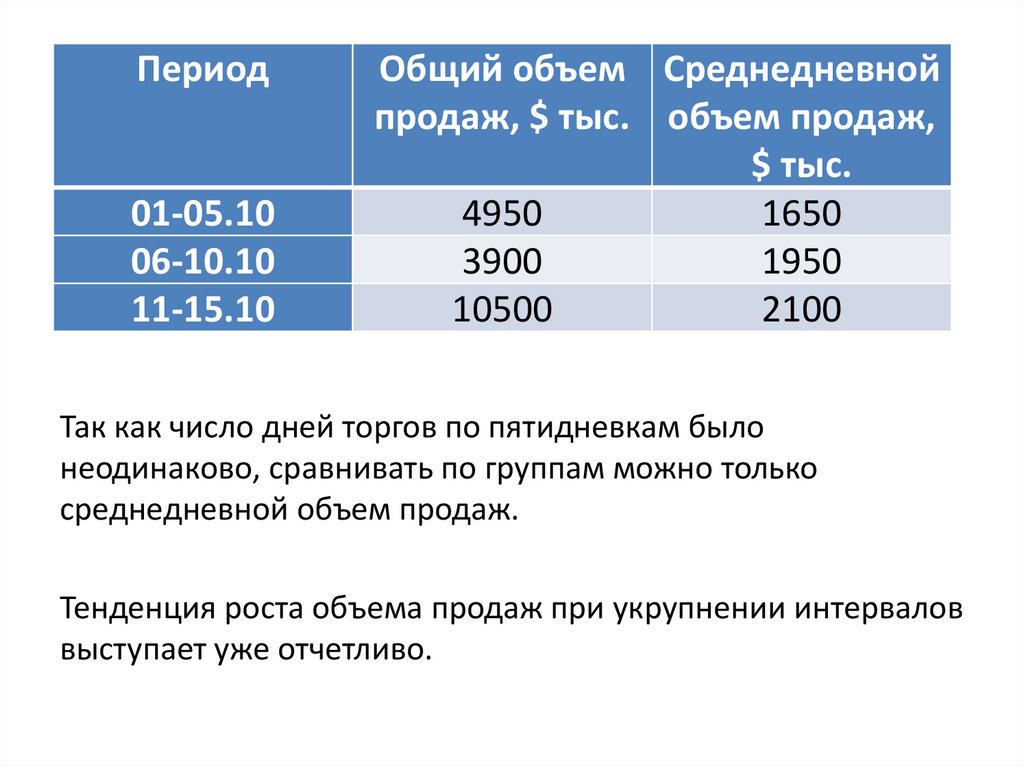
Пример. Имеются данные об объеме продаж
валюты на торгах ММВБ ($ тыс.):
01.10 02.10 05.10 06.10 07.10 11.10 12.10 13.10 14.10 15.10
1000 2200 1750 2300 1600 1800 2200 1900 2600 2000
В этих данных тенденция объема продаж
проявляется нечетко. Она затушевана колебаниями
уровней в отдельные дни.
Суточные данные заменим пятидневными

43.

Период
01-05.10
06-10.10
11-15.10
Общий объем Среднедневной
продаж, $ тыс. объем продаж,
$ тыс.
4950
1650
3900
1950
10500
2100
Так как число дней торгов по пятидневкам было
неодинаково, сравнивать по группам можно только
среднедневной объем продаж.
Тенденция роста объема продаж при укрупнении интервалов
выступает уже отчетливо.

44.

2) Метод скользящей средней –нахождение
средних уровней за определенные периоды
времени путем последовательного
передвижения начала периода на единицу
времени.
Например, если принять m = 3, то сначала
рассчитывается средняя величина из первых
трех уровней, затем находится средняя
величина из 2-го, 3-го и 4-го уровней, потом
из 3-го, 4-го и 5-го уровней и т. д.

45.

Каждый раз в сумме трех уровней появляется
новый уровень, а два остаются прежними, что
и обусловливает взаимопогашение
случайных колебаний в средних уровнях.
Скользящая средняя определяется по
средней арифметической простой и условно
относится к середине (центру) каждого
рассматриваемого интервала.

46.

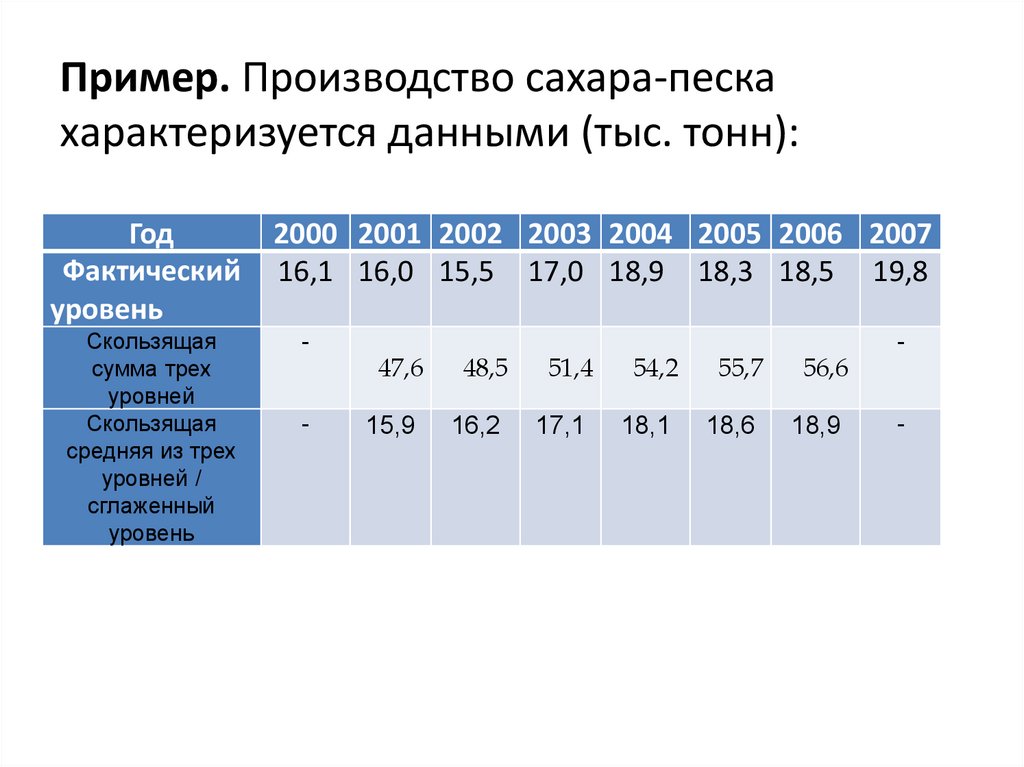
Пример. Производство сахара-песка
характеризуется данными (тыс. тонн):
Год
Фактический
уровень
Скользящая
сумма трех
уровней
Скользящая
средняя из трех
уровней /
сглаженный
уровень
2000 2001 2002 2003 2004 2005 2006 2007
16,1 16,0 15,5 17,0 18,9 18,3 18,5 19,8
-
-
47,6
48,5
51,4
54,2
55,7
56,6
15,9
16,2
17,1
18,1
18,6
18,9
-
-

47.

Сглаживание методом скользящей средней
можно проводить по любому числу членов m.
Чаще период скольжения (m) берется
нечетным, так как в этом случае скользящая
средняя относится к середине интервала и
динамический ряд сокращается на (m-1)/2
уровень с каждой стороны: в примере m= 3 и
ряд уменьшился на 2 уровня ( не стало
данных за 2000 и 2007 гг.).

48.

Если m — нечетное число, то скользящая средняя
сразу относится к конкретной временной точке —
середине интервала.
Если же m — четное, то скользящая средняя
относится к промежутку между временными
точками.
Тогда, чтобы сглаженные уровни относились
непосредственно к конкретным временным точкам,
находят центрированную скользящую среднюю как
среднее арифметическое из каждой пары смежных
промежуточных значений скользящих средних.
При четном m динамический ряд сокращается на
m/2 уровень с каждой стороны

49.

Например, при сглаживании по двум членам
(m = 2) средняя из первых двух уровней будет
находиться между первой и второй
временной точкой, следующая — между
второй и третьей точкой и т. д.
Центрированную скользящую среднюю определяют как среднее
арифметическое из каждой пары смежных промежуточных значений

50.

Метод скользящей средней устраняет лишь
случайные колебания.
Если ряд содержит сезонную волну, она
сохранится и после сглаживания данным
методом.
Кроме того, этот метод сглаживания, как и
метод укрупнения интервалов, не позволяет
выражать общую тенденцию изменения
уровней в виде математической модели.

51.

52.

53.

54.

55. Рекомендации при выборе функции

56.

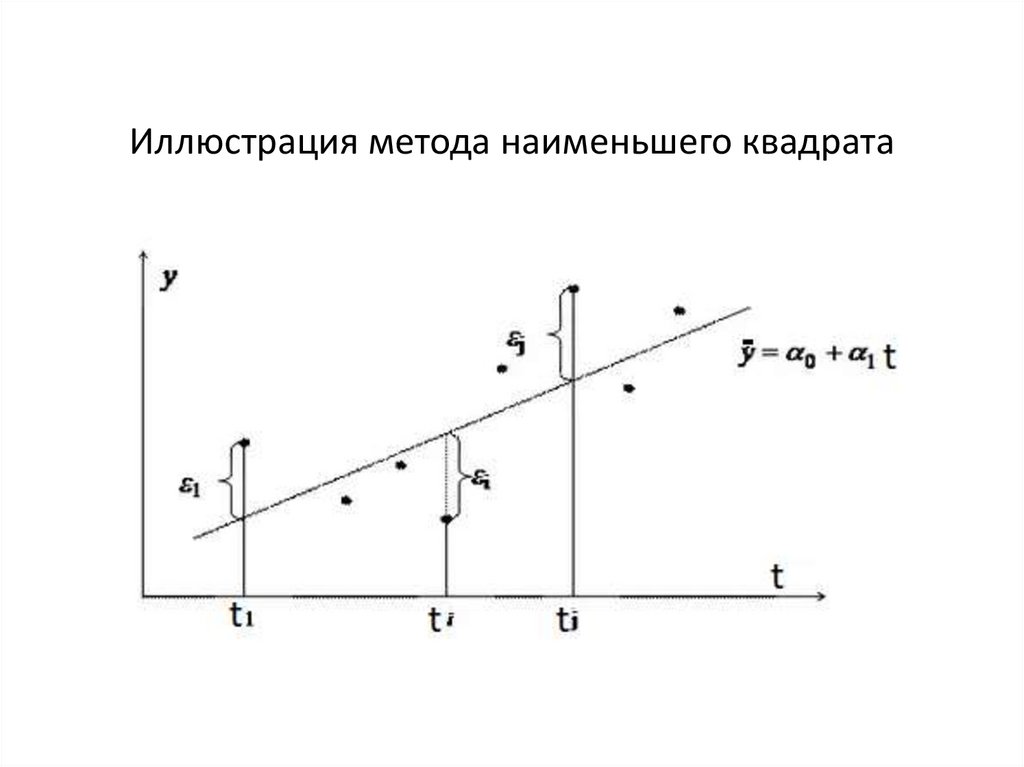
57. Иллюстрация метода наименьшего квадрата

58.

Выравнивание по линейной функции
Параметры а0 и а1 определяются путем решения системы нормальных
уравнений:

59.

Существуют готовые формулы для a0 и a1
следующим образом:

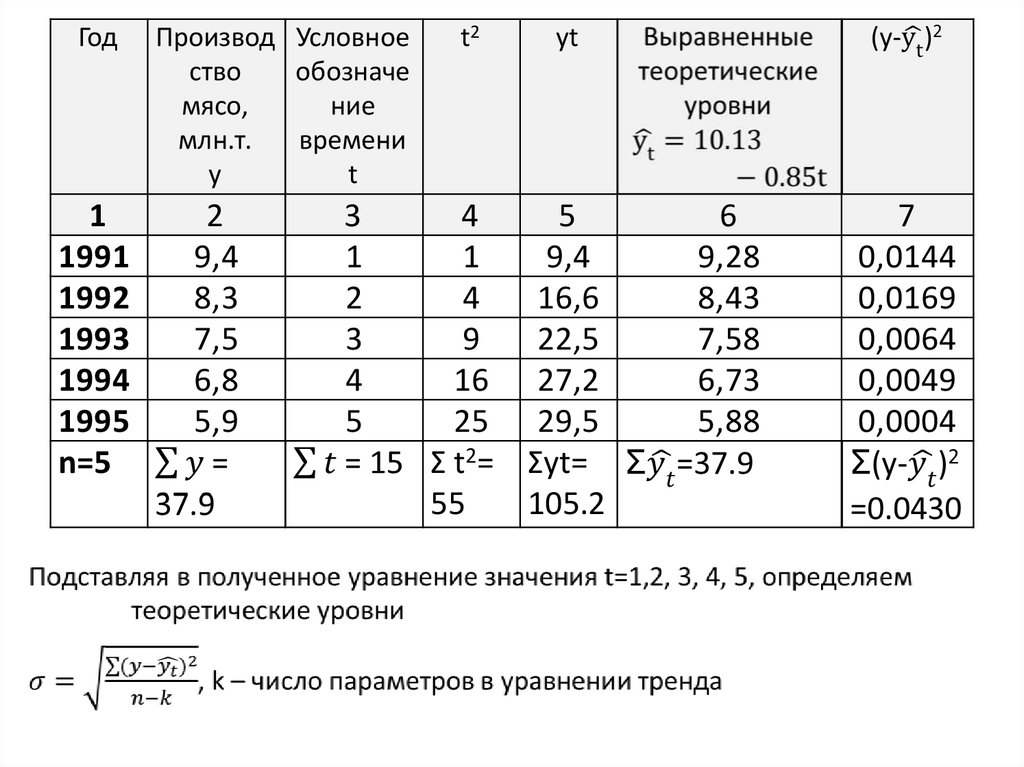
60. Пример, расчет теоретических уровней линейного ряда

Год
1
1991
1992
1993
1994
1995
Итого
Производство
мясо, млн.т.
2
9,4
8,3
7,5
6,8
5,9
37.9

61.

Год
Производств
Условное
о мясо,
обозначение
млн.т.
времени
y
t
1
1991
1992
1993
1994
1995
n=5
5а0 + 15a1 = 37,9,
l5a0 + 55а1 = 105,2.
2
9,4
8,3
7,5
6,8
5,9
3
1
2
3
4
5
t2
4
1
4
9
16
25
Ʃ t2=55
yt
5
9,4
16,6
22,5
27,2
29,5
Ʃyt=105.2

62.

Год
1
1991
1992
1993
1994
1995
n=5
Производ Условное
ство
обозначе
мясо,
ние
млн.т.
времени
y
t
2
9,4
8,3
7,5
6,8
5,9
3
1
2
3
4
5
t2
yt
4
5
1
9,4
4
16,6
9
22,5
16 27,2
25 29,5
Ʃ t2= Ʃyt=
55
105.2
6
9,28
8,43
7,58
6,73
5,88
7
0,0144
0,0169
0,0064
0,0049
0,0004

63.

Расчет параметров a0 и a1 упрощается, если отсчет
времени ведется от середины ряда.
Например, при нечетном числе уровней серединная
точка времени (год, месяц) принимается за нуль,
тогда предшествующие ей периоды обозначаются
соответственно цифрами −1, −2, −3 и т. д., а
следующие за ней — соответственно цифрами 1, 2,
3 и т. д.

64.

Год
Производс
тво мясо,
млн.т.
y
1
2
1991
9,4
1992
8,3
1993
7,5
1994
6,8
1995
5,9
итого 37.9
t
t2
yt
3
-2
-1
0
1
2
4
4
1
0
1
4
10
5
-18,8
-8,3
0
6,8
11,8
-8,5
а0 = 37.9/5 = 7.58
а1 = -8,5/10 = -0.85
6
9,28
8,43
7,58
6,73
5,88
37.9

65.

Коэффициенты регрессий а1 имеет
одинаковое значение (а1= - 0,85) и
характеризует средyее годовое изменение
(уменьшение) производства мяса в России за
период 1991 — 1995 гг.
В то же время параметр aQ (свободный член)
различен, поскольку отсчет ведется от
разного периода.
Поэтому каждый раз, записывая уравнение
тренда, необходимо указывать, от какой
временной точки ведется счет.

66.

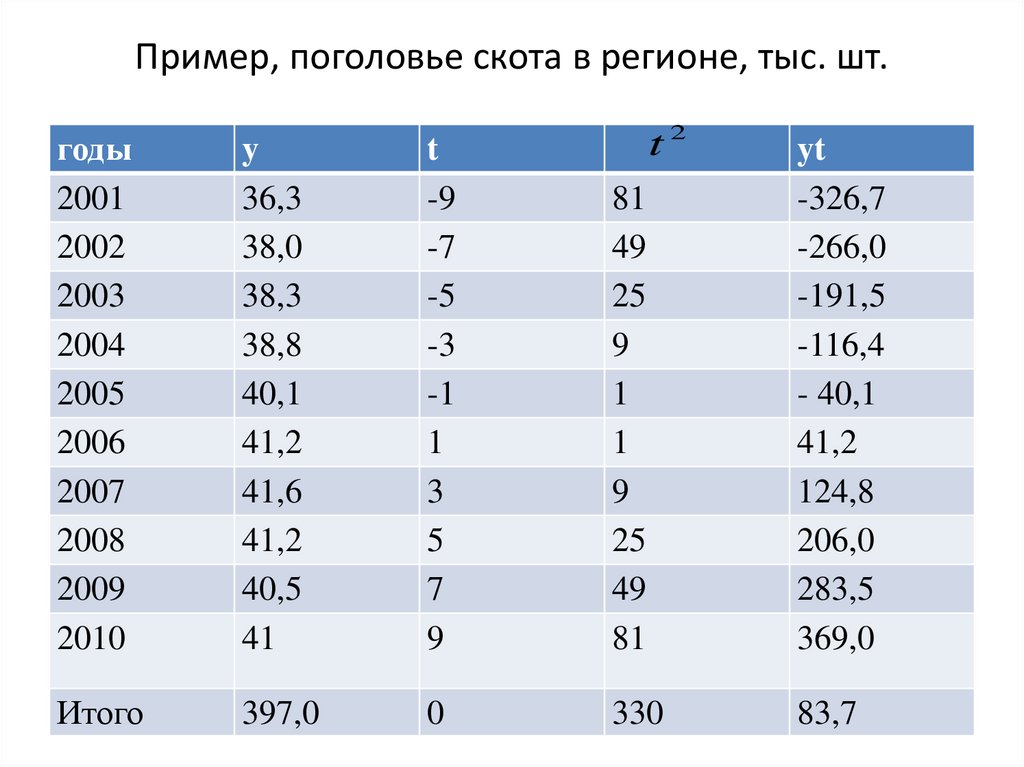
67. Пример, поголовье скота в регионе, тыс. шт.

t2
годы
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
y
36,3
38,0
38,3
38,8
40,1
41,2
41,6
41,2
40,5
41
t
-9
-7
-5
-3
-1
1
3
5
7
9
81
49
25
9
1
1
9
25
49
81
yt
-326,7
-266,0
-191,5
-116,4
- 40,1
41,2
124,8
206,0
283,5
369,0
Итого
397,0
0
330
83,7

68.

y
n
y t
2
t

69.

70.

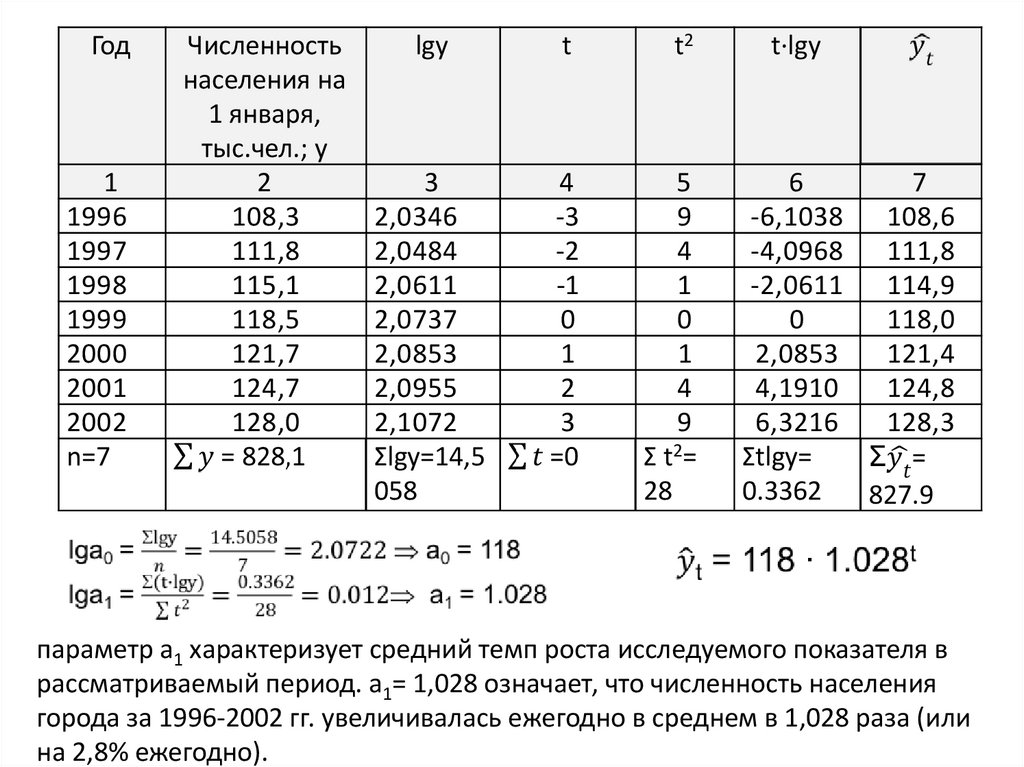
Год
1
1996
1997
1998
1999
2000
2001
2002
n=7
Численность
населения на
1 января,
тыс.чел.; y
2
108,3
111,8
115,1
118,5
121,7
124,7
128,0
lgy
t
t2
t∙lgy
3
2,0346
2,0484
2,0611
2,0737
2,0853
2,0955
2,1072
Ʃlgy=14,5
058
4
-3
-2
-1
0
1
2
3
5
9
4
1
0
1
4
9
Ʃ t2=
28
6
-6,1038
-4,0968
-2,0611
0
2,0853
4,1910
6,3216
Ʃtlgy=
0.3362
7
108,6
111,8
114,9
118,0
121,4
124,8
128,3
параметр а1 характеризует средний темп роста исследуемого показателя в
рассматриваемый период. а1= 1,028 означает, что численность населения
города за 1996-2002 гг. увеличивалась ежегодно в среднем в 1,028 раза (или
на 2,8% ежегодно).

71.

72.

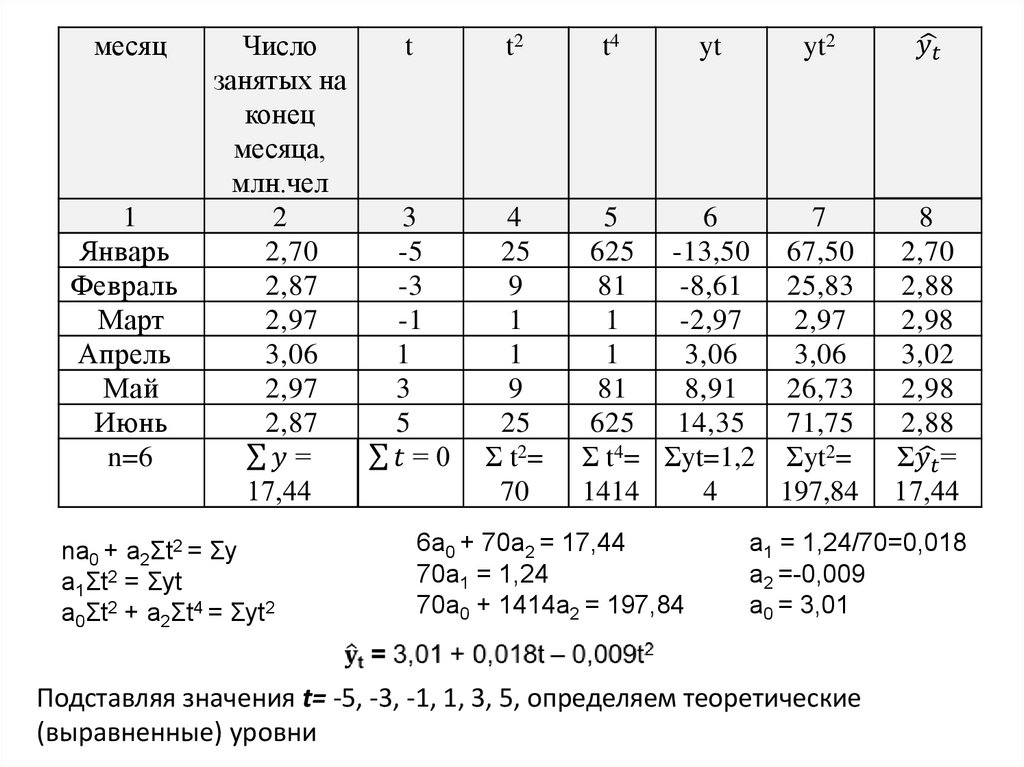
месяц
1
Январь
Февраль
Март
Апрель
Май
Июнь
n=6
Число
занятых на
конец
месяца,
млн.чел
2
2,70
2,87
2,97
3,06
2,97
2,87
na0 + a2Ʃt2 = Ʃy
a1Ʃt2 = Ʃyt
a0Ʃt2 + a2Ʃt4 = Ʃyt2
t
t2
3
-5
-3
-1
1
3
5
4
25
9
1
1
9
25
Ʃ t2=
70
t4
yt
yt2
5
6
7
625 -13,50 67,50
81
-8,61
25,83
1
-2,97
2,97
1
3,06
3,06
81
8,91
26,73
625
14,35 71,75
Ʃ t4= Ʃyt=1,2 Ʃyt2=
1414
4
197,84
6a0 + 70a2 = 17,44
70a1 = 1,24
70a0 + 1414a2 = 197,84
8
2,70
2,88
2,98
3,02
2,98
2,88
a1 = 1,24/70=0,018
a2 =-0,009
a0 = 3,01
Подставляя значения t= -5, -3, -1, 1, 3, 5, определяем теоретические
(выравненные) уровни

73.

74.

месяц
1
1995
1996
1997
1998
1999
2000
2001
n=7
Число
занятых на
конец
месяца,
млн.чел
2
93
77
61
48
40
40
40
1
2
3
4
5
6
7
t
1/t
(1/t)2
y/t
3
4
5
6
7
1,0000
93,0
0,2500
38,5
0,1089
20,3
0,0625
12,0
0,0400
8,0
0,0289
6,7
0,0196
5,7
Ʃ(1/t)2= Ʃy/t=
1.5099 184.2
98,8
65,5
54,5
49,0
45,8
43,5
42,0
1,00
0,50
0,33
0,25
0,20
0,17
0,14
Ʃ(1/t)=
2.59
7a0 + 2.59a1 = 399
2.59a0 + 1.5099a1= 184.2
а0 = 32,5
а1 = 66,3

75.

4. Выявление и измерение сезонных
колебаний в динамическом ряду
Сезонные колебания—это сравнительно
устойчивые внутригодичные колебания,
повторяющиеся из года в год, из месяца в
месяц (например, потребление
электроэнергии возрастает в зимние месяцы
и снижается в летние).

76.

77.

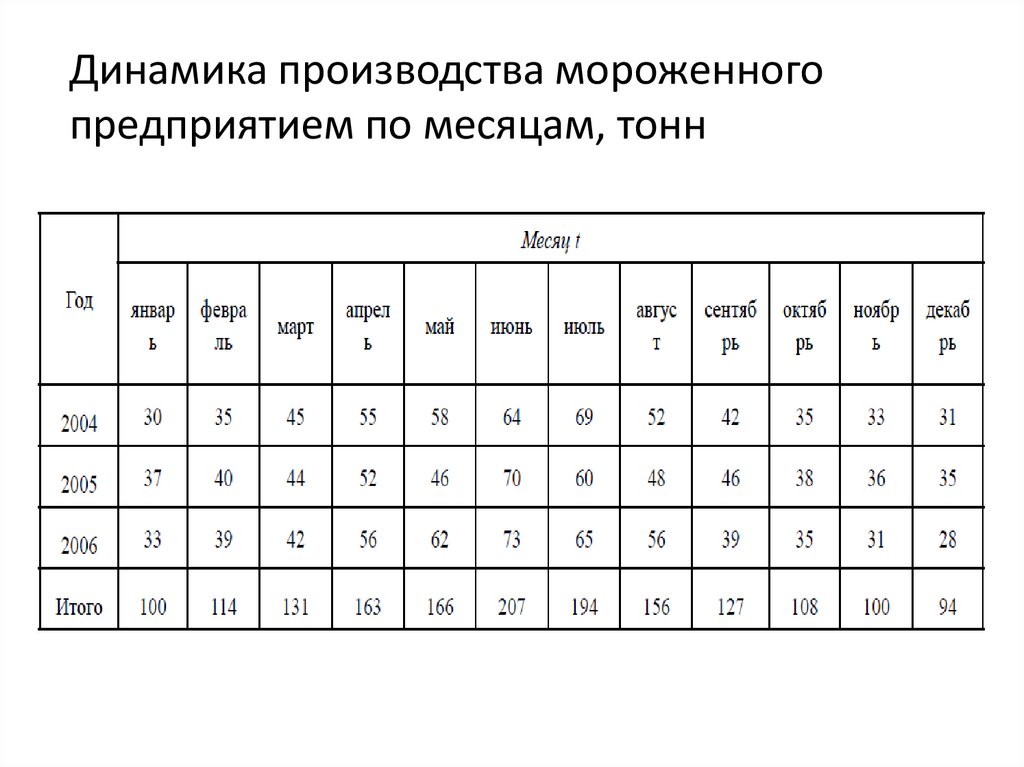
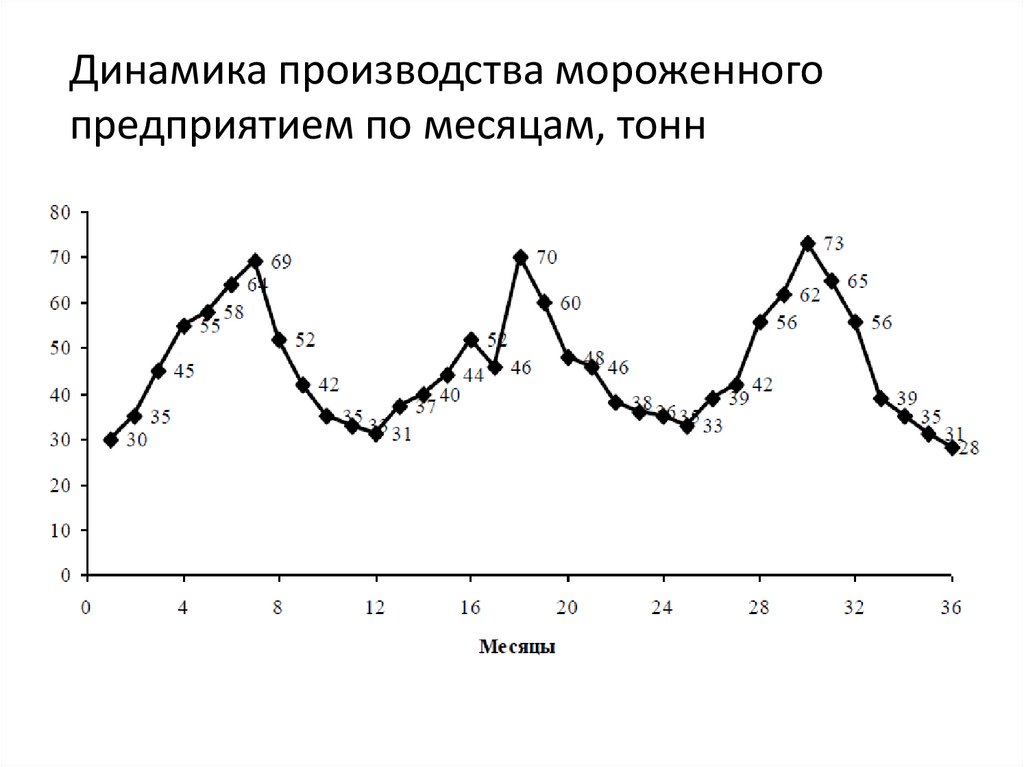
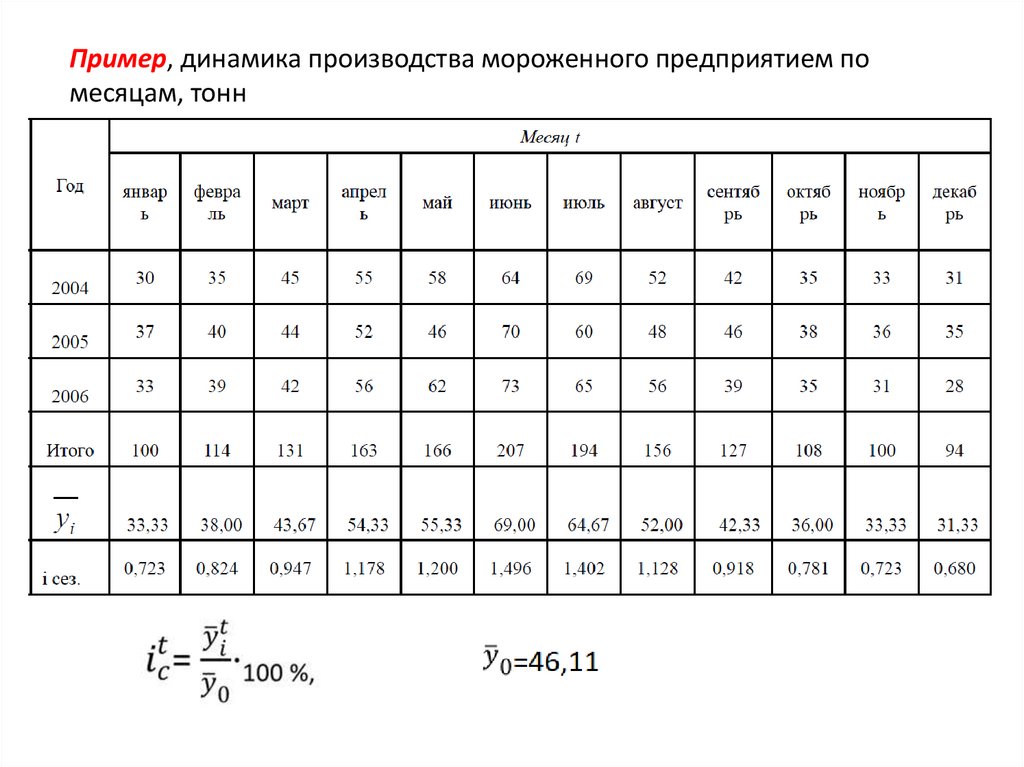
Динамика производства мороженного
предприятием по месяцам, тонн

78.

Динамика производства мороженного
предприятием по месяцам, тонн

79.

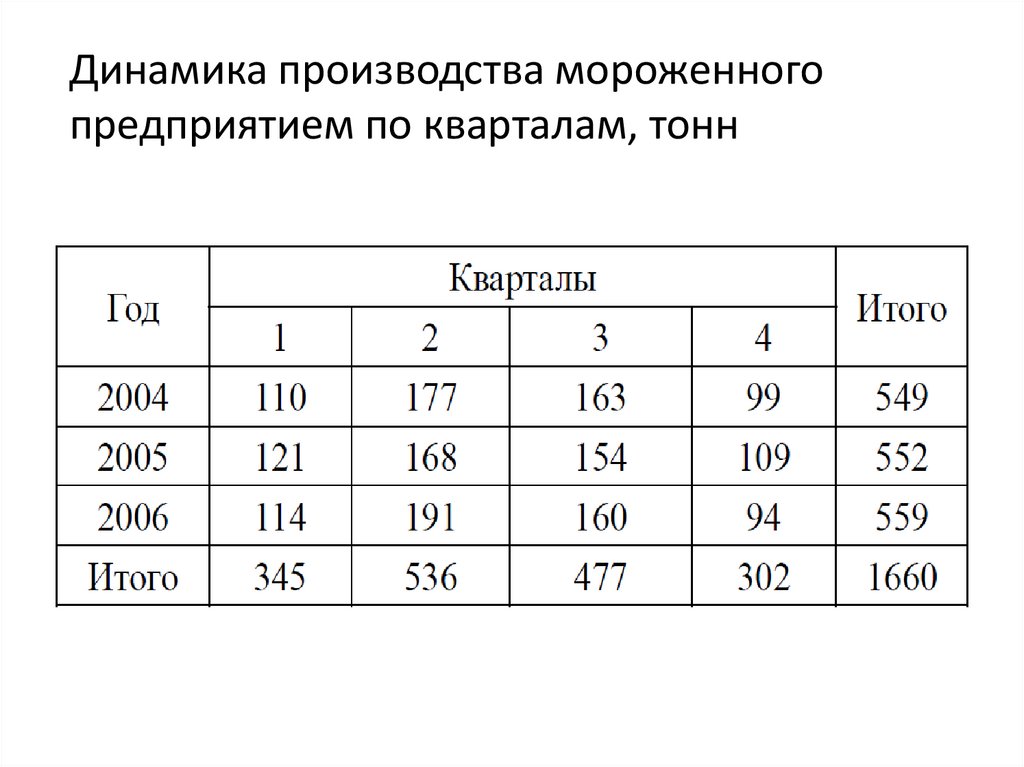
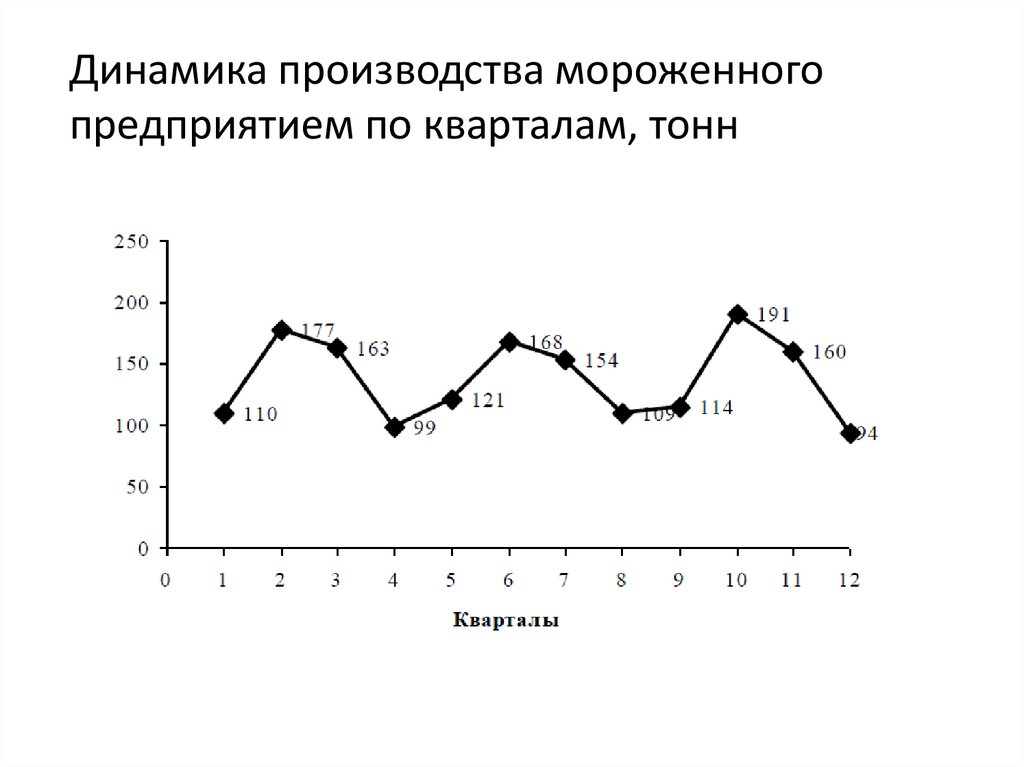
Динамика производства мороженного
предприятием по кварталам, тонн

80.

Динамика производства мороженного
предприятием по кварталам, тонн

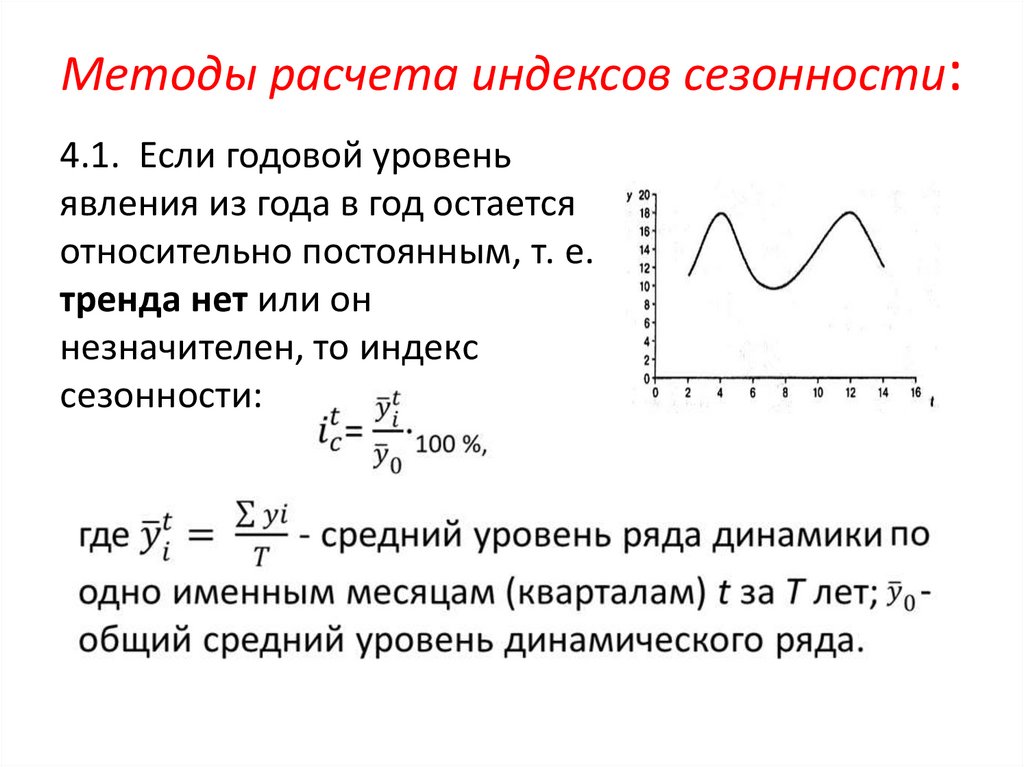
81. Методы расчета индексов сезонности:

4.1. Если годовой уровень
явления из года в год остается
относительно постоянным, т. е.
тренда нет или он
незначителен, то индекс
сезонности:

82.

Пример, динамика производства мороженного предприятием по
месяцам, тонн

83.

84.

85.

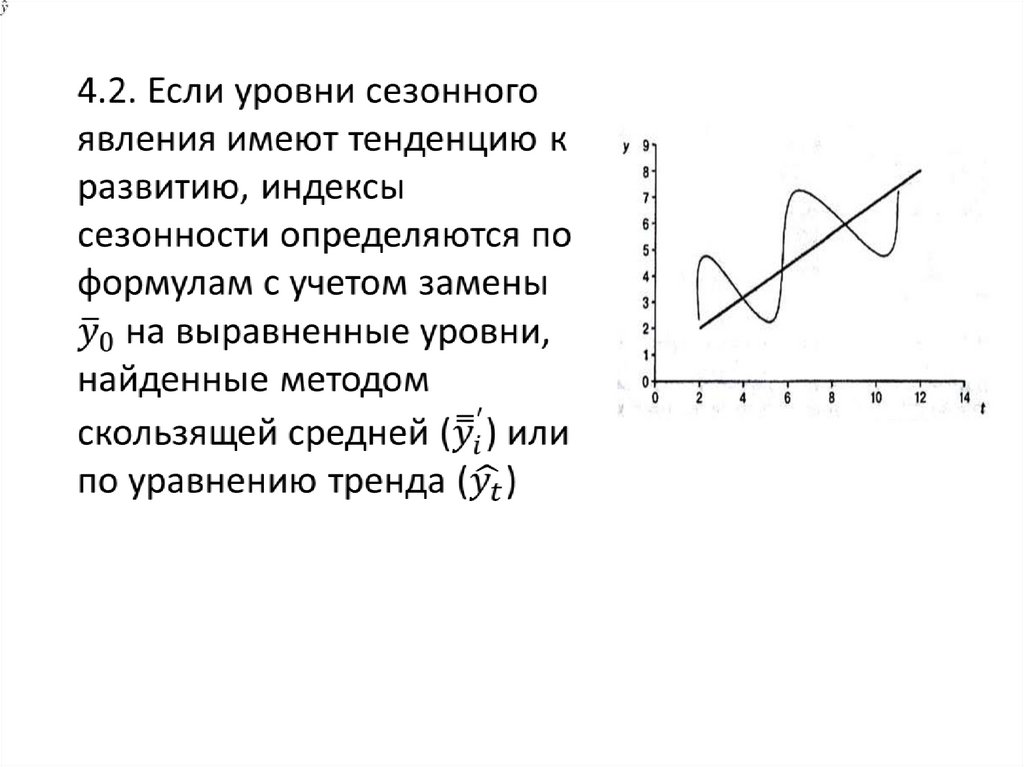
4.2.2. Индексы сезонности с использованием
тренда:
Если значения индексов сезонности разные
для одноименных месяцев и кварталов, то
находят их средние значения

86.

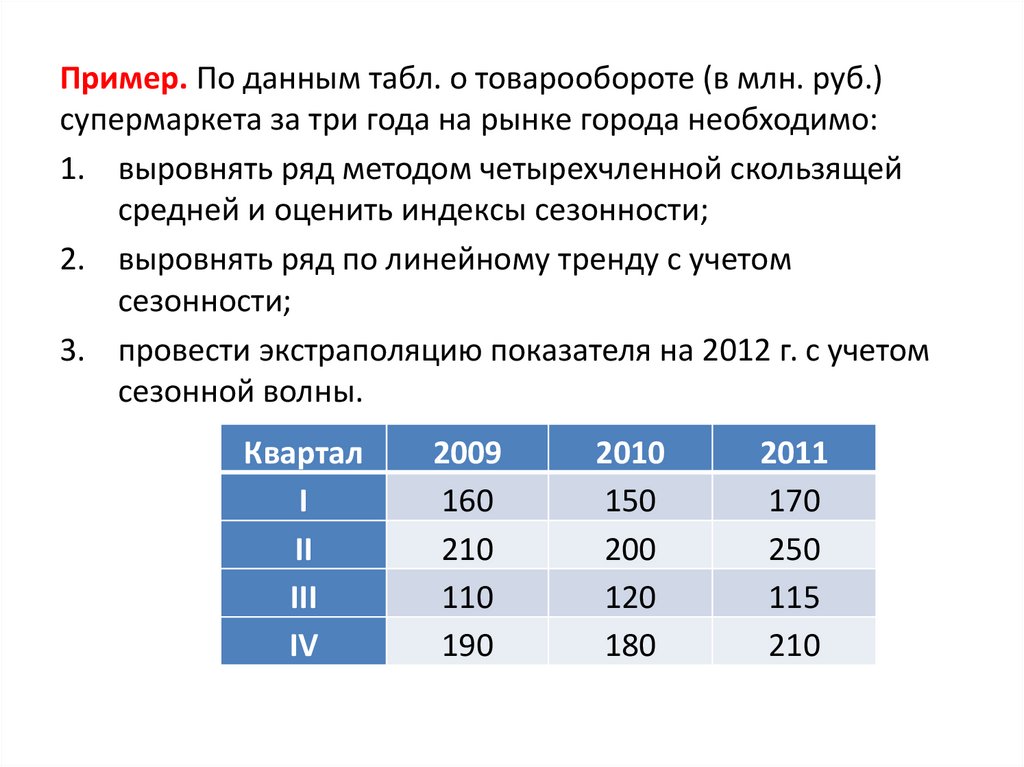
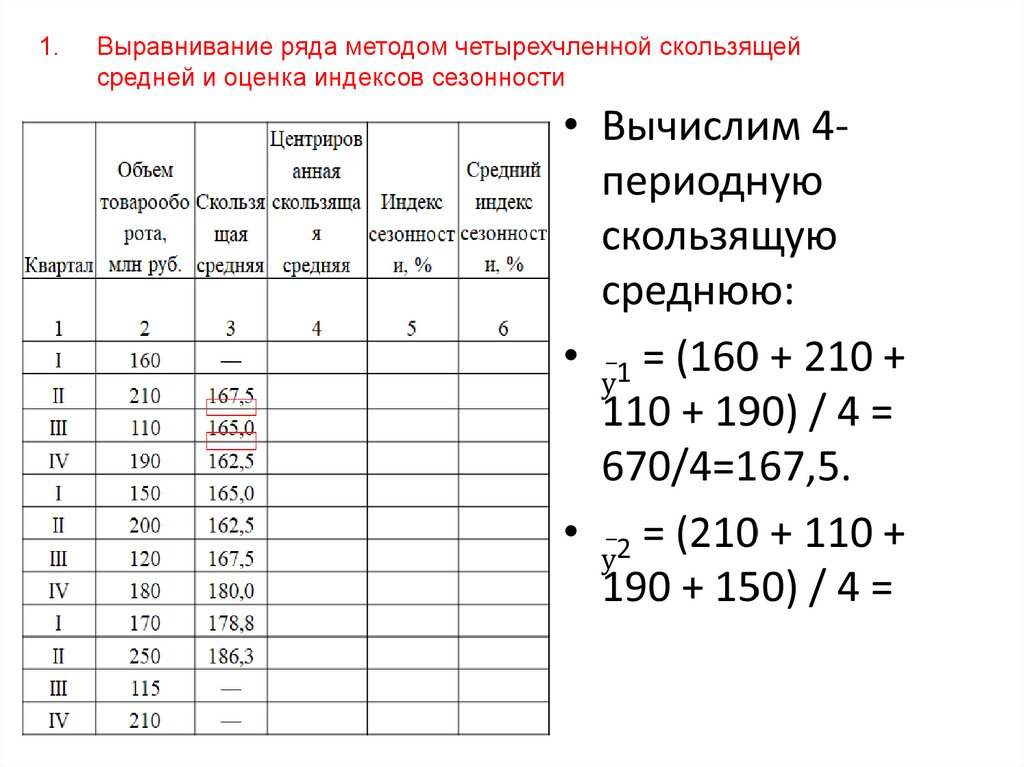
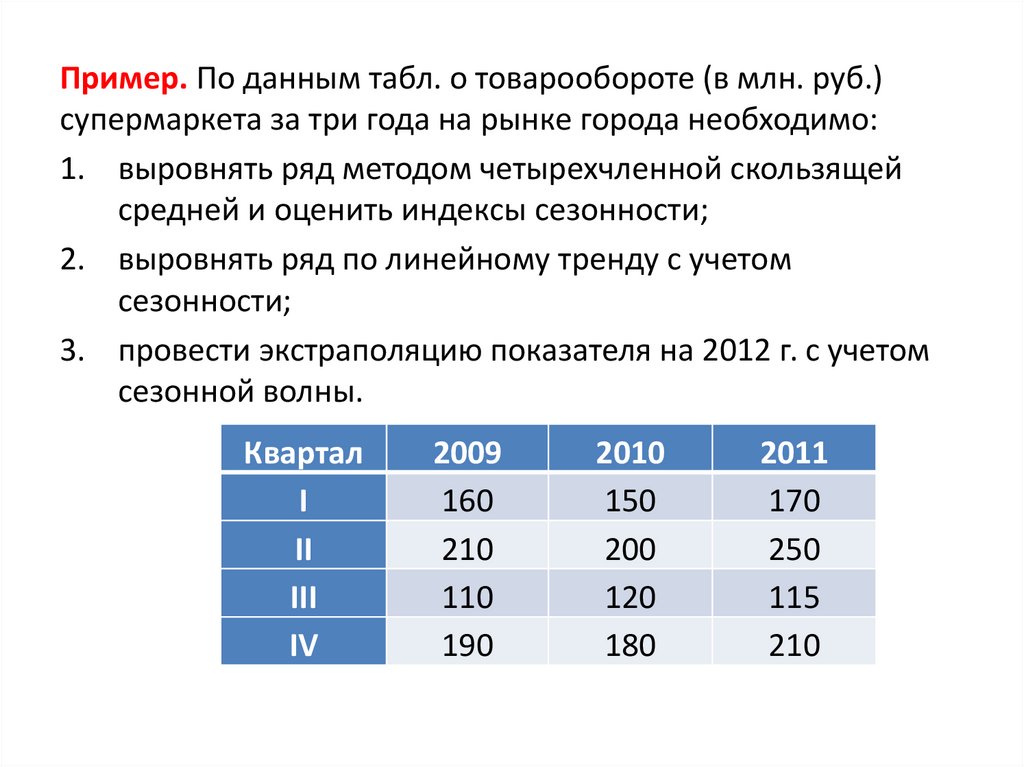
Пример. По данным табл. о товарообороте (в млн. руб.)
супермаркета за три года на рынке города необходимо:
1. выровнять ряд методом четырехчленной скользящей
средней и оценить индексы сезонности;
2. выровнять ряд по линейному тренду с учетом
сезонности;
3. провести экстраполяцию показателя на 2012 г. с учетом
сезонной волны.
Квартал
I
II
III
IV
2009
160
210
110
190
2010
150
200
120
180
2011
170
250
115
210

87.

1.
Выравнивание ряда методом четырехчленной скользящей
средней и оценка индексов сезонности

88.

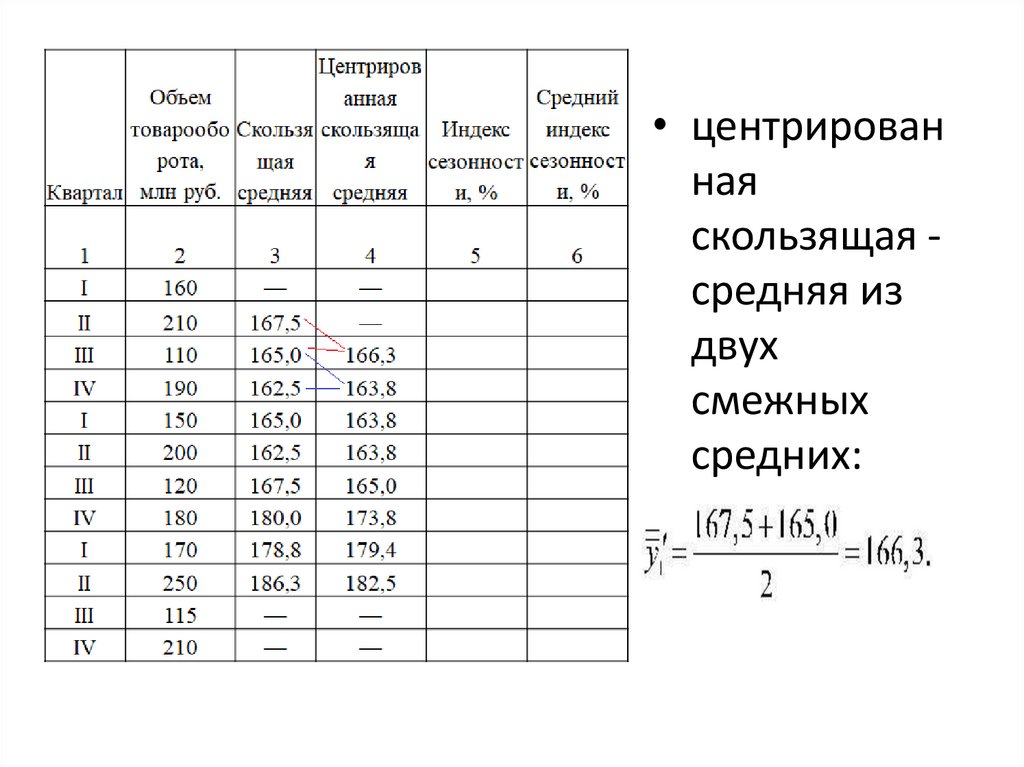
• центрирован
ная
скользящая средняя из
двух
смежных
средних:

89.

Центриро
Объем Скольз ванная
Средний
товарооб ящая скользящ Индекс индекс
Кварта орота, средня
ая
сезоннос сезоннос
л
млн руб.
я
средняя ти, %
ти, %
1
I
2
160
3
—
4
—
5=
(2/4)*100
—
II
III
IV
I
II
III
IV
I
II
III
IV
210
110
190
150
200
120
180
170
250
115
210
167,5
165,0
162,5
165,0
162,5
167,5
180,0
178,8
186,3
—
—
—
166,3
163,8
163,8
163,8
165,0
173,8
179,4
182,5
—
—
—
66,2
116,0
91,6
122,1
72,7
103,6
94,8
137,0
—
—
6

90.

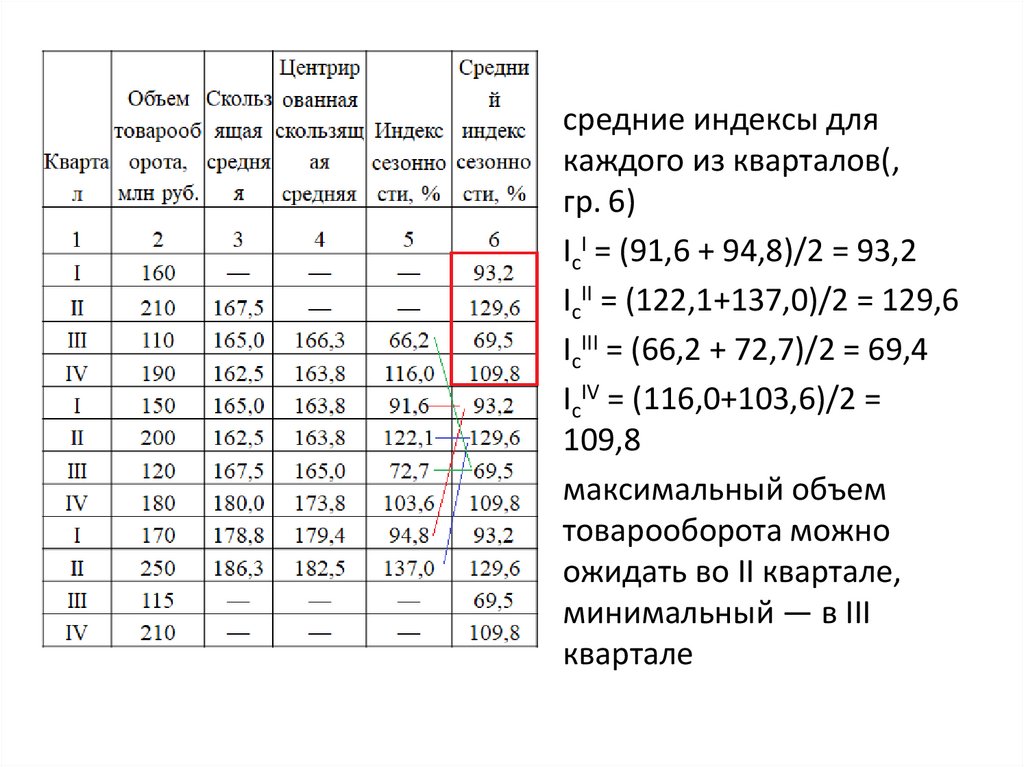
средние индексы для
каждого из кварталов(,
гр. 6)
IcI = (91,6 + 94,8)/2 = 93,2
IcII = (122,1+137,0)/2 = 129,6
IcIII = (66,2 + 72,7)/2 = 69,4
IcIV = (116,0+103,6)/2 =
109,8
максимальный объем
товарооборота можно
ожидать во II квартале,
минимальный — в III
квартале

91.

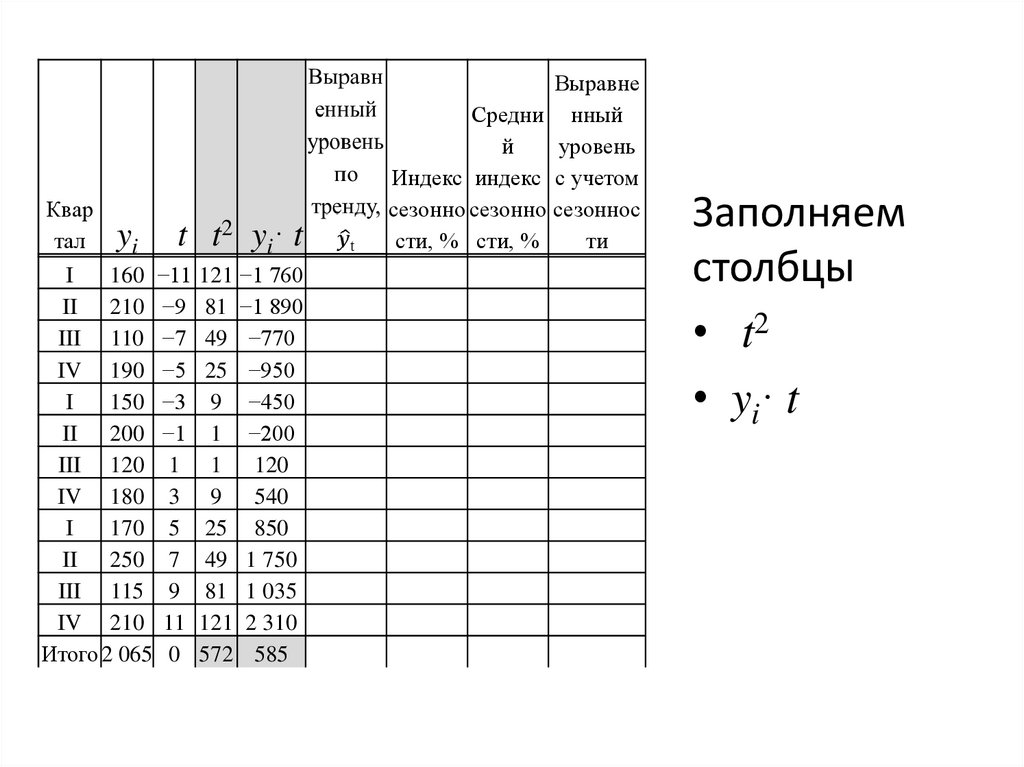
2) Выравнивание ряда по линейному тренду с учетом сезонности
Квар
тал
Объем
товар
ообор
ота
yi
t t 2 y i· t
I
160 −11
II
210 −9
III 110 −7
IV 190 −5
I
150 −3
II
200 −1
III 120 1
IV 180 3
I
170 5
II
250 7
III 115 9
IV 210 11
Итого 2 065 0
Выравнен
ный
Средний уровень
Индекс индекс с учетом
сезонно сезонно сезонност
сти, % сти, %
и
введем
параметр
времени t
так, чтобы
∑t = 0

92.

Квар
тал
yi
t
t2
y i· t
I
160 −11 121 −1 760
II 210 −9 81 −1 890
III 110 −7 49 −770
IV 190 −5 25 −950
I
150 −3 9 −450
II 200 −1 1 −200
III 120 1 1 120
IV 180 3 9 540
I
170 5 25 850
II 250 7 49 1 750
III 115 9 81 1 035
IV 210 11 121 2 310
Итого 2 065 0 572 585
Выравне
Средни нный
й
уровень
Индекс индекс с учетом
сезонно сезонно сезоннос
сти, % сти, %
ти
Заполняем
столбцы
• t2
• yi· t

93.

Квар
тал
yi
t t 2 y i· t
I
160 −11 121 −1 760
II 210 −9 81 −1 890
III 110 −7 49 −770
IV 190 −5 25 −950
I
150 −3 9 −450
II 200 −1 1 −200
III 120 1 1 120
IV 180 3 9 540
I
170 5 25 850
II 250 7 49 1 750
III 115 9 81 1 035
IV 210 11 121 2 310
Итого 2 065 0 572 585
Выравне
Средни нный
й
уровень
Индекс индекс с учетом
сезонно сезонно сезоннос
сти, % сти, %
ти

94.

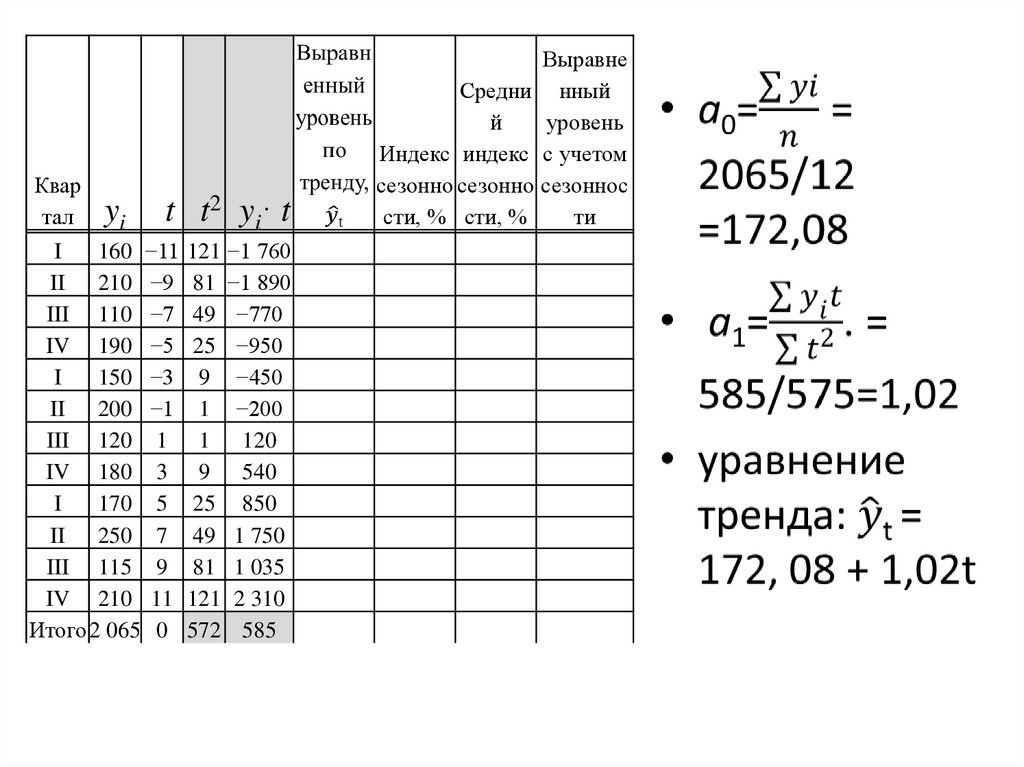
Квар
тал
yi
t t 2 y i· t
I
160 −11 121 −1 760 160,8
II 210 −9 81 −1 890 162,9
III 110 −7 49 −770 164,9
IV 190 −5 25 −950 167,0
I
150 −3 9 −450 169,0
II 200 −1 1 −200 171,1
III 120 1 1
120
173,1
IV 180 3 9
540
175,2
I
170 5 25 850
177,2
II 250 7 49 1 750 179,2
III 115 9 81 1 035 181,3
IV 210 11 121 2 310 183,3
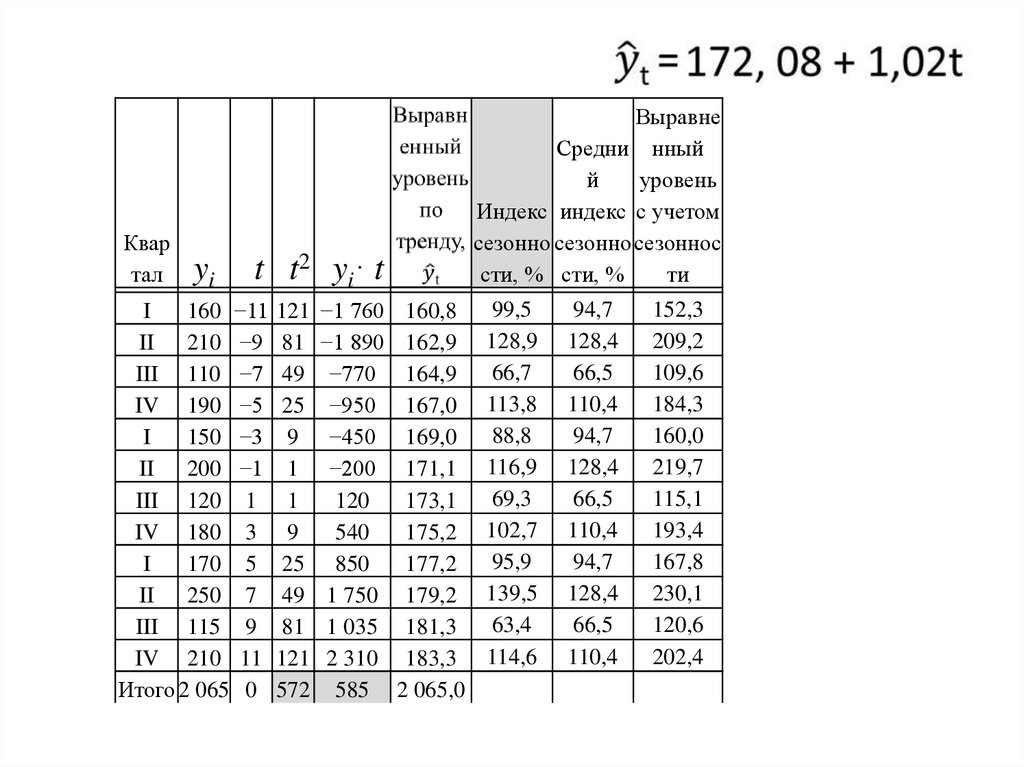
Итого2 065 0 572 585 2 065,0
Средн Выравне
ий
нный
индекс уровень
Индекс сезонн с учетом
сезонно ости, сезонно
сти, %
%
сти
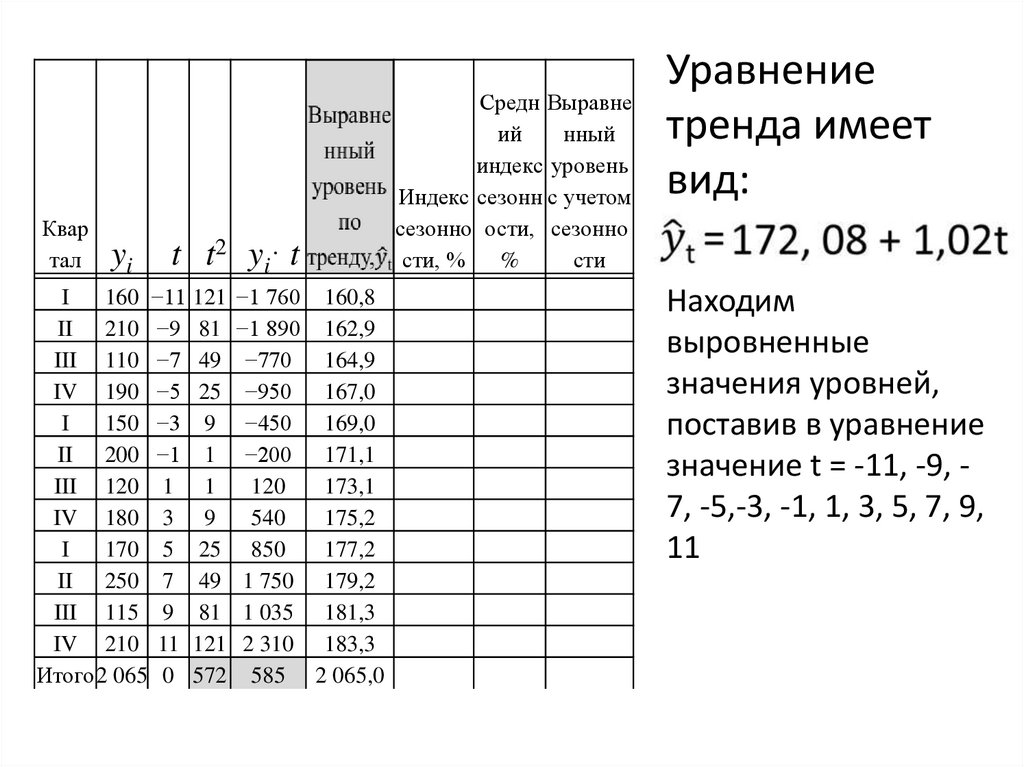
Уравнение
тренда имеет
вид:
Находим
выровненные
значения уровней,
поставив в уравнение
значение t = -11, -9, 7, -5,-3, -1, 1, 3, 5, 7, 9,
11

95.

Квар
тал
yi
t t 2 y i· t
I
160 −11 121 −1 760 160,8
II 210 −9 81 −1 890 162,9
III 110 −7 49 −770 164,9
IV 190 −5 25 −950 167,0
I
150 −3 9 −450 169,0
II 200 −1 1 −200 171,1
III 120 1 1
120
173,1
IV 180 3 9
540
175,2
I
170 5 25 850
177,2
II 250 7 49 1 750 179,2
III 115 9 81 1 035 181,3
IV 210 11 121 2 310 183,3
Итого 2 065 0 572 585 2 065,0
Выравне
Средни нный
й
уровень
Индекс индекс с учетом
сезонно сезонно сезоннос
сти, % сти, %
ти
99,5
128,9
66,7
113,8
88,8
116,9
69,3
102,7
95,9
139,5
63,4
114,6
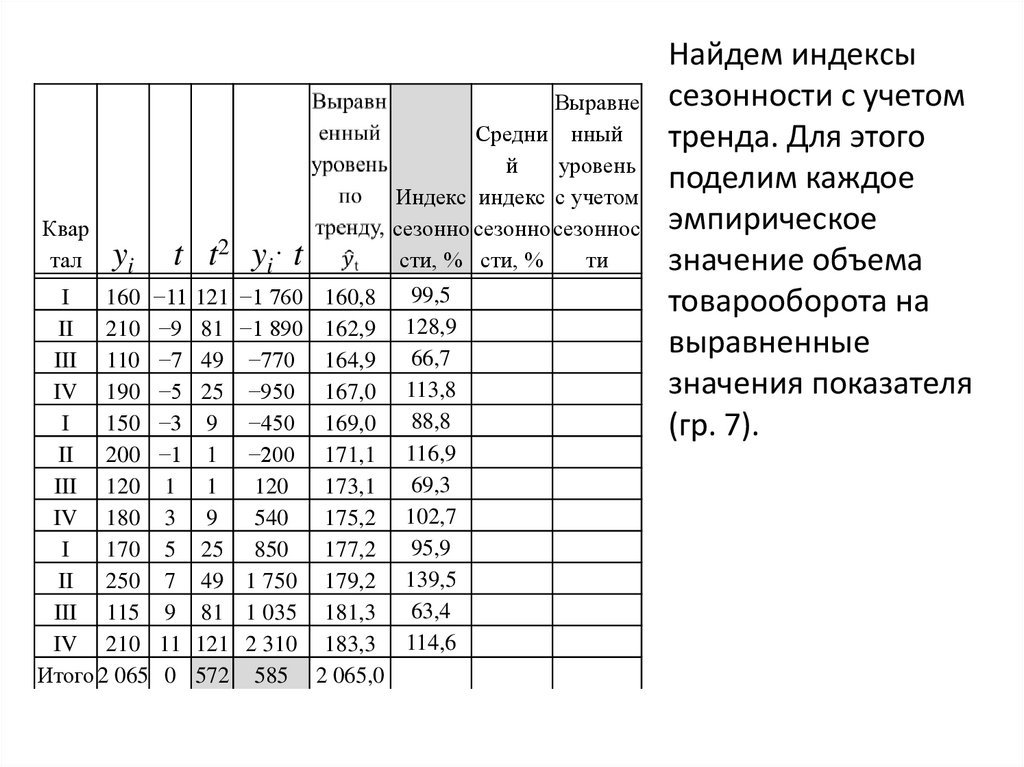
Найдем индексы
сезонности с учетом
тренда. Для этого
поделим каждое
эмпирическое
значение объема
товарооборота на
выравненные
значения показателя
(гр. 7).

96.

Квар
тал
yi
t t 2 y i· t
I
160 −11 121 −1 760 160,8
II 210 −9 81 −1 890 162,9
III 110 −7 49 −770 164,9
IV 190 −5 25 −950 167,0
I
150 −3 9 −450 169,0
II 200 −1 1 −200 171,1
III 120 1 1
120
173,1
IV 180 3 9
540
175,2
I
170 5 25 850
177,2
II 250 7 49 1 750 179,2
III 115 9 81 1 035 181,3
IV 210 11 121 2 310 183,3
Итого 2 065 0 572 585 2 065,0
Выравне
Средни нный
й
уровень
Индекс индекс с учетом
сезонно сезонно сезоннос
сти, % сти, %
ти
99,5
128,9
66,7
113,8
88,8
116,9
69,3
102,7
95,9
139,5
63,4
114,6
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
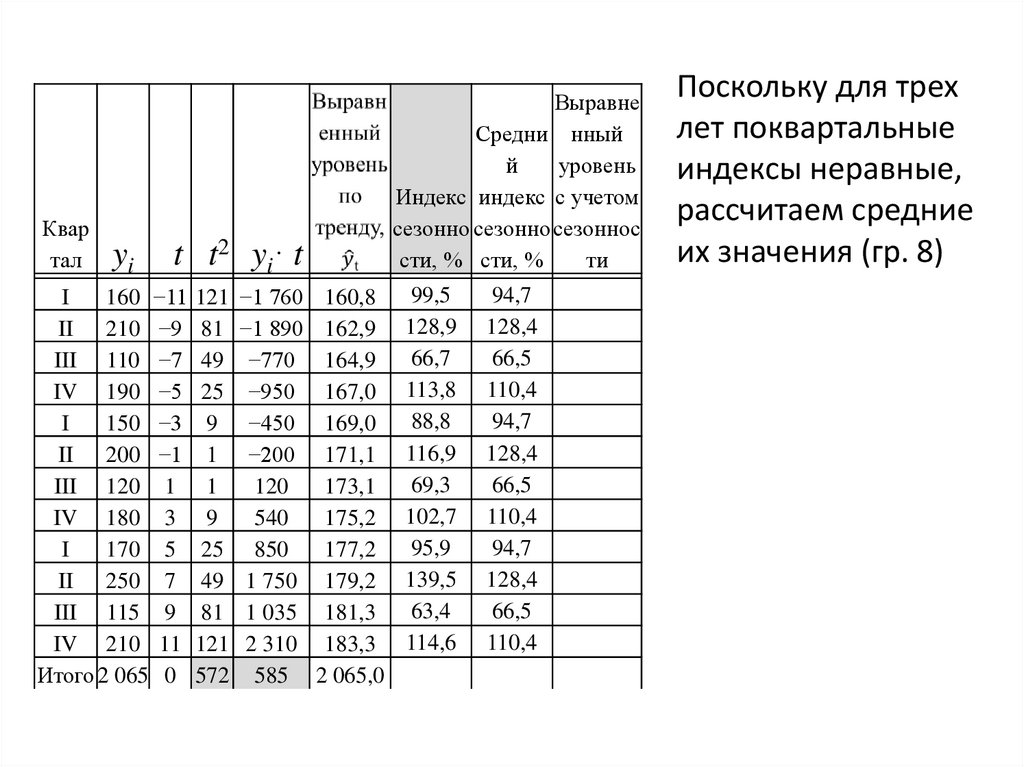
Поскольку для трех
лет поквартальные
индексы неравные,
рассчитаем средние
их значения (гр. 8)

97.

Квар
тал
yi
t t 2 y i· t
I
160 −11 121 −1 760 160,8
II 210 −9 81 −1 890 162,9
III 110 −7 49 −770 164,9
IV 190 −5 25 −950 167,0
I
150 −3 9 −450 169,0
II 200 −1 1 −200 171,1
III 120 1 1
120
173,1
IV 180 3 9
540
175,2
I
170 5 25 850
177,2
II 250 7 49 1 750 179,2
III 115 9 81 1 035 181,3
IV 210 11 121 2 310 183,3
Итого 2 065 0 572 585 2 065,0
Выравне
Средни нный
й
уровень
Индекс индекс с учетом
сезонно сезонно сезоннос
сти, % сти, %
ти
99,5
128,9
66,7
113,8
88,8
116,9
69,3
102,7
95,9
139,5
63,4
114,6
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
152,3
209,2
109,6
184,3
160,0
219,7
115,1
193,4
167,8
230,1
120,6
202,4
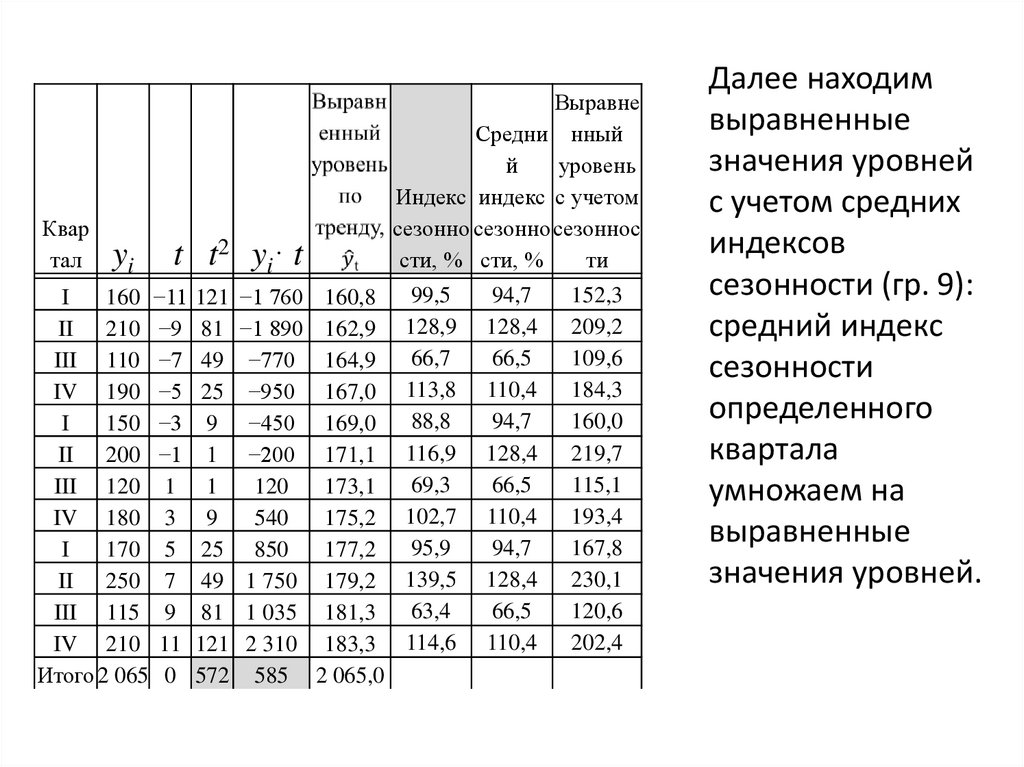
Далее находим
выравненные
значения уровней
с учетом средних
индексов
сезонности (гр. 9):
средний индекс
сезонности
определенного
квартала
умножаем на
выравненные
значения уровней.

98.

Квар
тал
yi
t t 2 y i· t
I
160 −11 121 −1 760 160,8
II 210 −9 81 −1 890 162,9
III 110 −7 49 −770 164,9
IV 190 −5 25 −950 167,0
I
150 −3 9 −450 169,0
II 200 −1 1 −200 171,1
III 120 1 1
120
173,1
IV 180 3 9
540
175,2
I
170 5 25 850
177,2
II 250 7 49 1 750 179,2
III 115 9 81 1 035 181,3
IV 210 11 121 2 310 183,3
Итого 2 065 0 572 585 2 065,0
Выравне
Средни нный
й
уровень
Индекс индекс с учетом
сезонно сезонно сезоннос
сти, % сти, %
ти
99,5
128,9
66,7
113,8
88,8
116,9
69,3
102,7
95,9
139,5
63,4
114,6
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
152,3
209,2
109,6
184,3
160,0
219,7
115,1
193,4
167,8
230,1
120,6
202,4
2 065,0
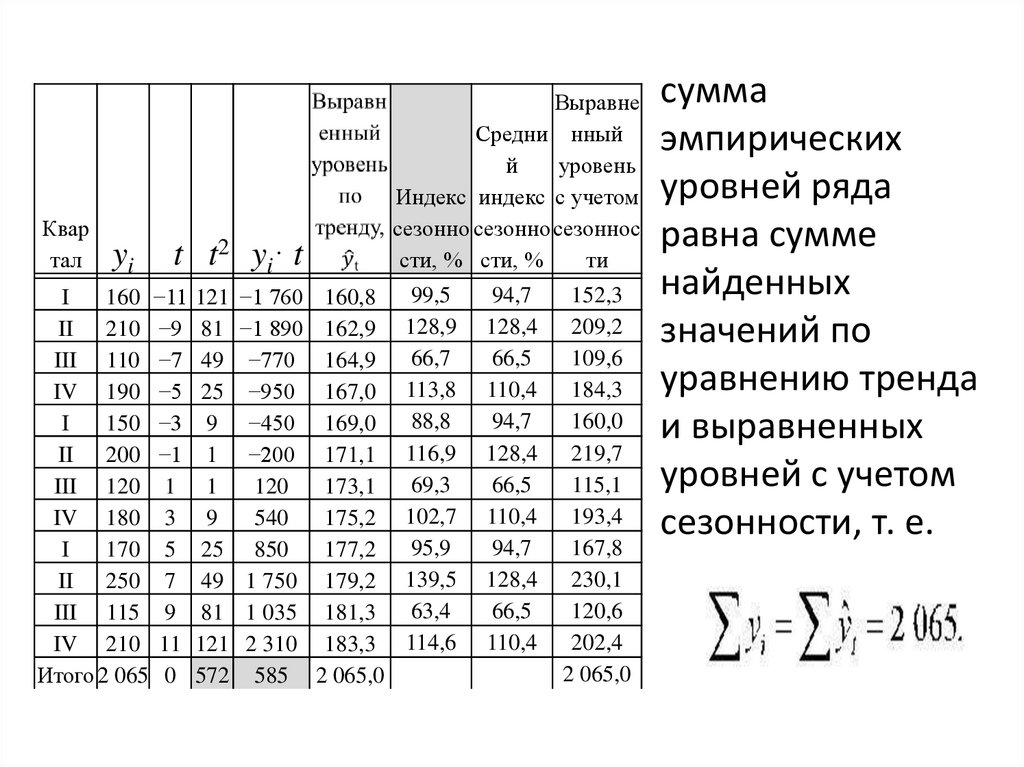
сумма
эмпирических
уровней ряда
равна сумме
найденных
значений по
уравнению тренда
и выравненных
уровней с учетом
сезонности, т. е.

99.

5. Прогнозирование развития явления
(показателя) на будущее.
Возможность прогнозирования основана на
предположении, что закономерность развития
явления, действовавшая в прошлом, сохранится и в
будущие периоды времени.
Выделяют два вида прогнозов:
• Экстраполяция —нахождение значений уровня
за пределами динамического ряда,
• Интерполяция — нахождение недостающих
значений показателя в пределах динамического
ряда.

100. Методы прогнозирования

5.1. На основе среднего уровня абсолютного
прироста

101.

5.2. На основе среднего коэффициента
роста:
Где
— средний коэффициент роста за n
периодов времени.

102.

5.3. На основе аналитического
выравнивания тренда, когда в уравнение
тренда подставляется соответствующее
значение независимой переменной времени
t за пределами исследуемого периода. Кроме
этого, на основе индексов сезонности и
тренда можно спрогнозировать ряд
динамики

103.

104.

Пример. По данным табл. о товарообороте (в млн. руб.)
супермаркета за три года на рынке города необходимо:
1. выровнять ряд методом четырехчленной скользящей
средней и оценить индексы сезонности;
2. выровнять ряд по линейному тренду с учетом
сезонности;
3. провести экстраполяцию показателя на 2012 г. с учетом
сезонной волны.
Квартал
I
II
III
IV
2009
160
210
110
190
2010
150
200
120
180
2011
170
250
115
210

105.

Квар
тал
yi
t t 2 y i· t
I
160 −11 121 −1 760 160,8
II 210 −9 81 −1 890 162,9
III 110 −7 49 −770 164,9
IV 190 −5 25 −950 167,0
I
150 −3 9 −450 169,0
II 200 −1 1 −200 171,1
III 120 1 1
120
173,1
IV 180 3 9
540
175,2
I
170 5 25 850
177,2
II 250 7 49 1 750 179,2
III 115 9 81 1 035 181,3
IV 210 11 121 2 310 183,3
Итого 2 065 0 572 585 2 065,0
Выравне
Средни нный
й
уровень
Индекс индекс с учетом
сезонно сезонно сезоннос
сти, % сти, %
ти
99,5
128,9
66,7
113,8
88,8
116,9
69,3
102,7
95,9
139,5
63,4
114,6
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
94,7
128,4
66,5
110,4
152,3
209,2
109,6
184,3
160,0
219,7
115,1
193,4
167,8
230,1
120,6
202,4

106.

3. Экстраполяция показателя на 2012 г. с
учетом сезонной волны
Зная уравнение тренда и сезонную волну,
спрогнозируем значение объема
товарооборота на четыре квартала 2012 г.
Значение параметра t в 2012 г.:
для I квартала — 13,
для II квартала — 15,
для III квартала— 17, д
ля IV квартала — 19.

107.

Подставляя данные значения в уравнение тренда и
умножая получившееся значение на средний
квартальный индекс сезонности, получаем прогноз:
• на I квартал 2012 г.: = (172,08 + 1,02 ∙ 13) ∙ 0,947 =
176 (млн руб.);
• на II квартал 2012 г.: = (172,08 + 1,02 ∙ 15) ∙ 1,284 =
246 (млн руб.);
• на III квартал 2012 г.: = (172,08 + 1,02 ∙ 17) ∙ 0,667
= 126 (млн руб.);
• на IV квартал 2012 г.: = (172,08 + 1,02 ∙ 19) ∙ 1,138
= 211 (млн руб.).