Численные методы решения обыкновенных дифференциальных уравнений

1.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ЗАДАЧА
КОШИ

2.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Понятие о дифференциальном уравнении

8.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
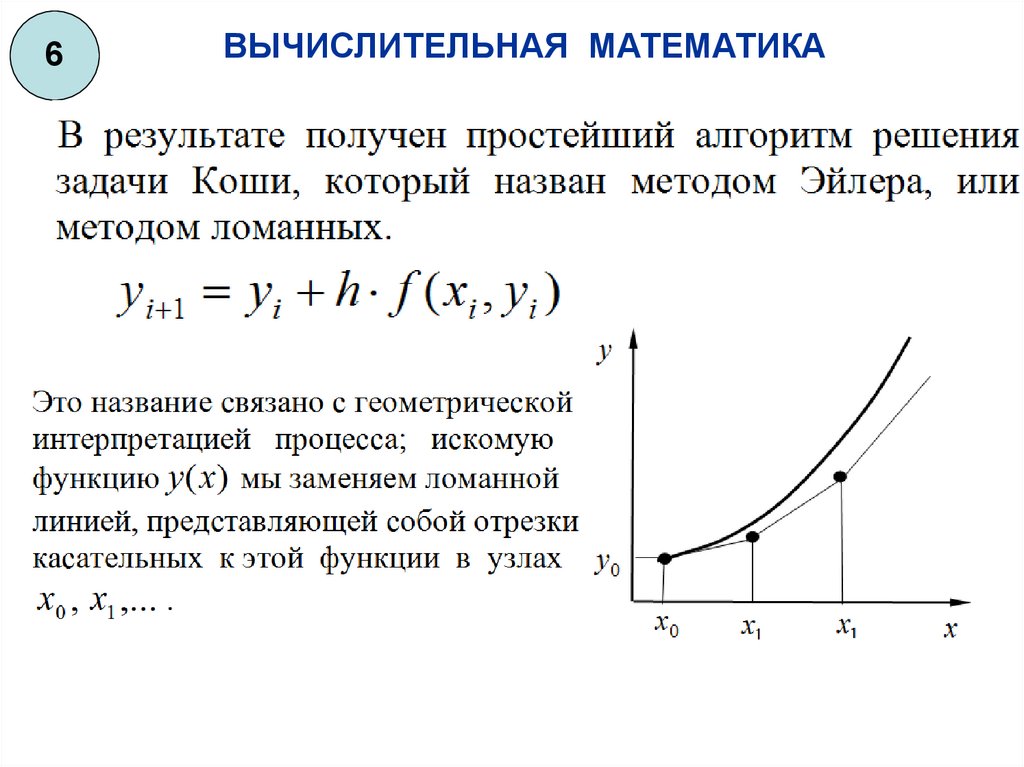
Метод
Эйлера

13.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Модификации метода Эйлера

14.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
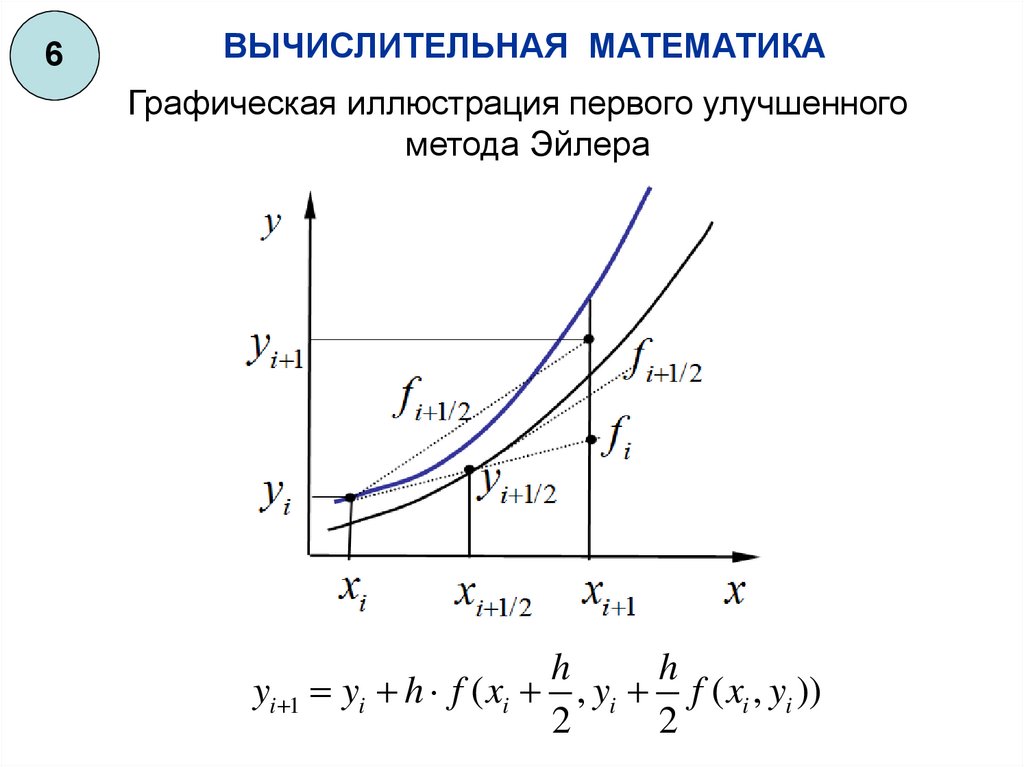
Графическая иллюстрация первого улучшенного
метода Эйлера
h
h
yi 1 yi h f ( xi , yi f ( xi , yi ))
2
2

15.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Модификации метода Эйлера

16.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
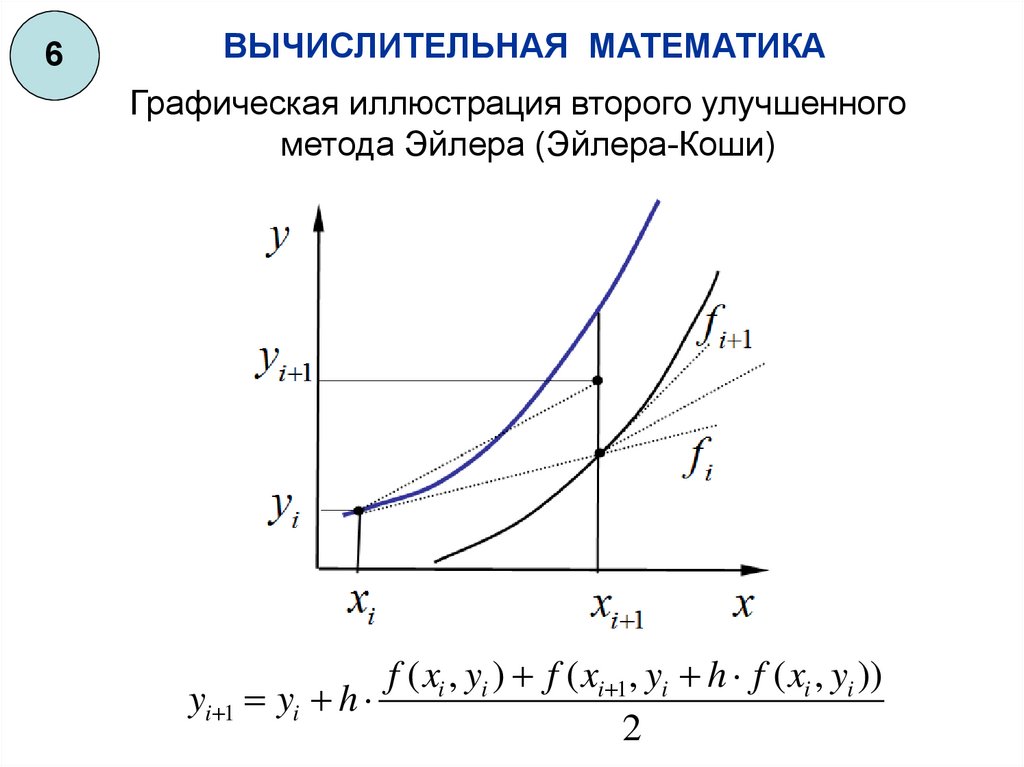
Графическая иллюстрация второго улучшенного
метода Эйлера (Эйлера-Коши)
f ( xi , yi ) f ( xi 1, yi h f ( xi , yi ))
yi 1 yi h
2

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод
Рунге-Кутты
Наибольшее распространение в практике вычислений
получили выражения, описывающие метод Рунге-Кутты
четвертого порядка:
k1i hf ( xi , yi ),
i
k
h
k2i hf ( xi , yi 1 ),
2
2
i
k
h
k3i hf ( xi , yi 2 ),
2
2
k4i hf ( xi h, yi k3i ),
yi 1 yi yi ,
1 i
yi (k1 2k2i 2k3i k4i ).
6

18.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
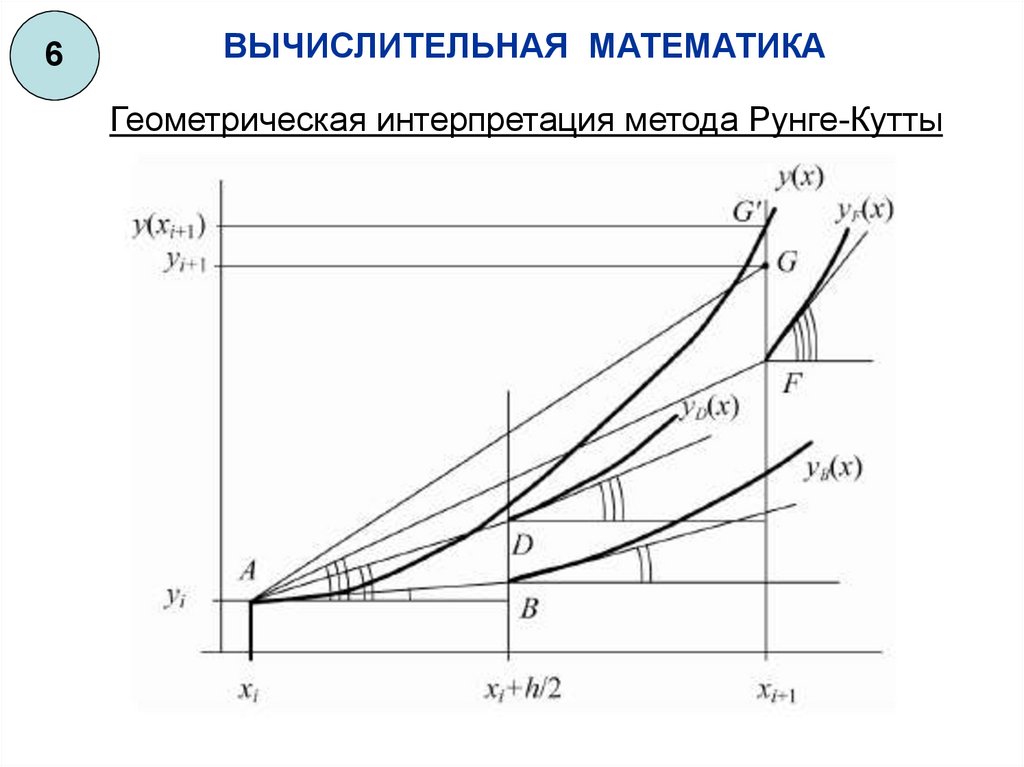
Геометрическая интерпретация метода Рунге-Кутты

19.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

20.

6
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
Метод Кутты – Мерсона (4 порядка точности)
k1i f ( xi , yi ),
h
h i
k f ( xi , yi k1 ),
3
3
h
h i h i
i
k3 f ( xi , yi k1 k 2 ),
3
6
6
h
h i 3h i
i
k 4 f ( xi , yi k1 k 2 ),
2
8
8
h i 3h i
i
k5 f ( xi h, yi k1 k3 2hk4i ),
2
2
h i
~
yi 1 yi k1 3k3i 4k 4i ,
2
h
yi 1 yi k1i 4k 4i k5i .
6
i
2