Методы численного решения обыкновенных дифференциальных уравнений. Формулы метода Рунге-Кутта

1.

МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Суть многих методов можно понять разлагая xi+1 x(ti + t) в ряд Тейлора:
xi+1 = xi + Vi t + 1/2 аi ( t)2 + О[( t)3].
(3.1)
Vi+1 = Vi + аi t + О[( t)2],
(3.2)
Здесь введено обозначение V = x’(t) , a = x’’(t). Хорошо известный метод
Эйлера эквивалентен сохранению в (3.1) и (3.2) членов О( t).
Один из методов, используемый при численном решении дифф. уравнений –
метод Рунге-Кутта 2-го порядка. Для объяснения метода рассмотрим ОДУ 1-го
порядка
dy
f ( x, y ).
dx
(3.3)
Формулы метода Рунге-Кутта 2-го порядка для уравнения (*.3) можно записать
в стандартных обозначениях:
k1 = f(xi,yi) x,
k2 = f(xi + x/2, yi + k1/2) x,
yi+1 = yi + k2 + О[( x)3] .
(3.4)
1

2.

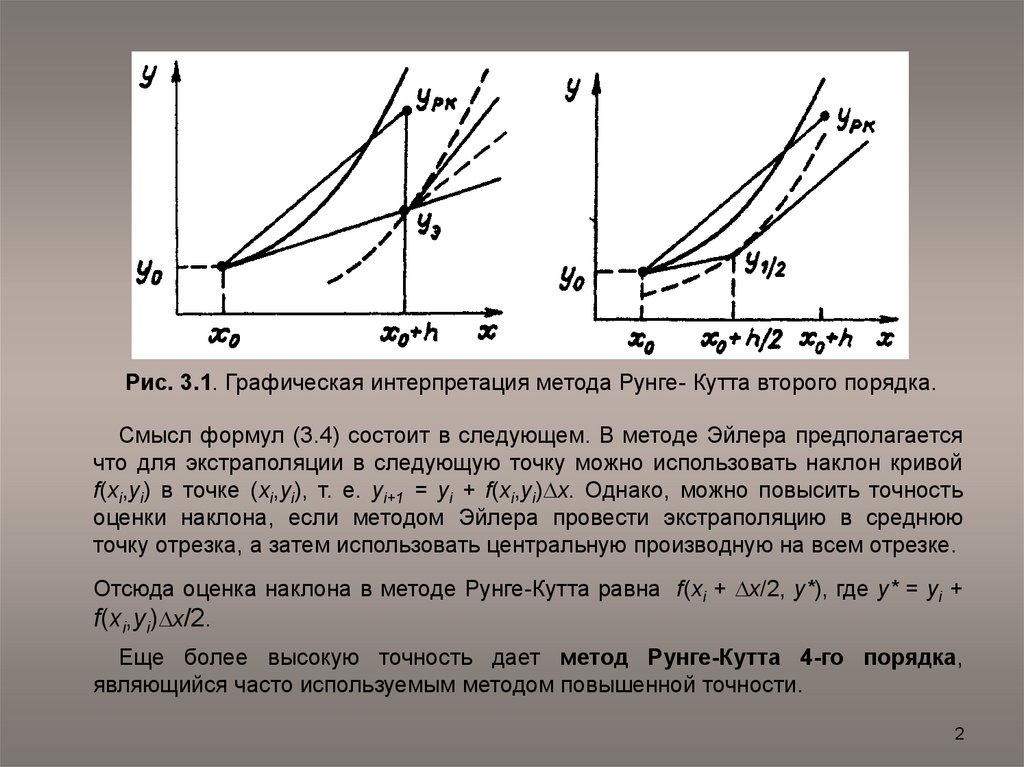
Рис. 3.1. Графическая интерпретация метода Рунге- Кутта второго порядка.
Смысл формул (3.4) состоит в следующем. В методе Эйлера предполагается
что для экстраполяции в следующую точку можно использовать наклон кривой
f(xi,yi) в точке (xi,yi), т. е. yi+1 = yi + f(xi,yi) x. Однако, можно повысить точность
оценки наклона, если методом Эйлера провести экстраполяцию в среднюю
точку отрезка, а затем использовать центральную производную на всем отрезке.
Отсюда оценка наклона в методе Рунге-Кутта равна f(xi + x/2, y*), где y* = yi +
f(xi,yi) x/2.
Еще более высокую точность дает метод Рунге-Кутта 4-го порядка,
являющийся часто используемым методом повышенной точности.
2

3.

(3.5)
Этот метод весьма прост и довольно эффективен в обычных расчетах.
Методы Рунге—Кутта легко программируются. Они обладают достаточными для
широкого круга задач свойствами точности и устойчивости, являются
самостартующими и позволяют легко изменять шаг интегрирования.
Увеличивая число вспомогательных точек, можно построить методы Рунге—
Кутта любого порядка точности p. В современных программах, реализующих
методы Рунге—Кутта, обязательно используется некоторый алгоритм
автоматического изменения шага интегрирования hn+1 = tn+1 – tn.
Локальная погрешность на шаге, согласно правилу Рунге может быть найдена
согласно выражению:
(3.6)
3

4.

Методы Адамса
В одношаговых методах после того как найдено очередное значение уn в точке
tn, значение yn-1 отбрасывают и уже не используют в последующих вычислениях.
Естественно попытаться извлечь определенную пользу из информации о
значениях решения уn-k+1, …, уn-1, уn не в одной, а в k предыдущих точках tn-k+1,
…, tn-1, tn , т.е. применить многошаговый метод.
Среди многошаговых методов наибольшее распространение в практике
вычислений получили методы Адамса.
(3.7)
Здесь 0, 1, …, k — числовые коэффициенты, fn+1-j = f(tn+1-j, yn+1-j). Уравнение
(*.7) позволяет найти новое значение уn+1, используя найденные ранее значения
уn, уn-1, уn-k+1. Поэтому предварительно требуется задание k начальных значений
у0, у1, …, уk-1. В случае 0 = 0 метод Адамса является явным, так как значение
yn+1 выражается через найденные ранее значения по явной формуле
(3.8)
Если же 0 0, то для нахождения yn+1 приходится решать нелинейное
уравнение
4

5.

Приведем расчетные формулы методов Адамса—Башфорта р-го порядка
точности при р = 2, 3, 4:
(3.9)
Приведем также расчетные формулы методов Адамса—Моултона р-го
порядка точности при р = 2, 3, 4.
(3.10)
Может показаться, что при наличии явных формул Адамса высокого порядка
точности нет необходимости в использовании неявных формул.
5

6.

Однако в вычислительной практике явные методы Адамса используются редко.
Одна из основных причин этого состоит в том, что в представляющих
наибольший интерес для приложений задачах неявные методы обладают
лучшими свойствами устойчивости и позволяют вести расчет с существенно
большими шагами, нежели явные методы.
Встроенная функция пакета MathCad для решения ОДУ Оdesolve(V,t, tmax, N)
позволяет пользователю после щелчка по имени функции выбирать метод
численных вычислений по которому она будет работать.
Метод Адамса (BDF), с постоянным шагом – метод Рунге-Кутта 4-го порядка с
постоянным шагом интегрирования, адаптивный – метод Рунге-Кутта 4-го
порядка с переменным шагом интегрирования либо жёсткий – метод Радаус.
Рис. 3.2. Выбор метода работы
функции Odesolve.
6