Похожие презентации:
Две стороны одного треугольника пропорциональны двум сторонам другого треугольника
1.
2.
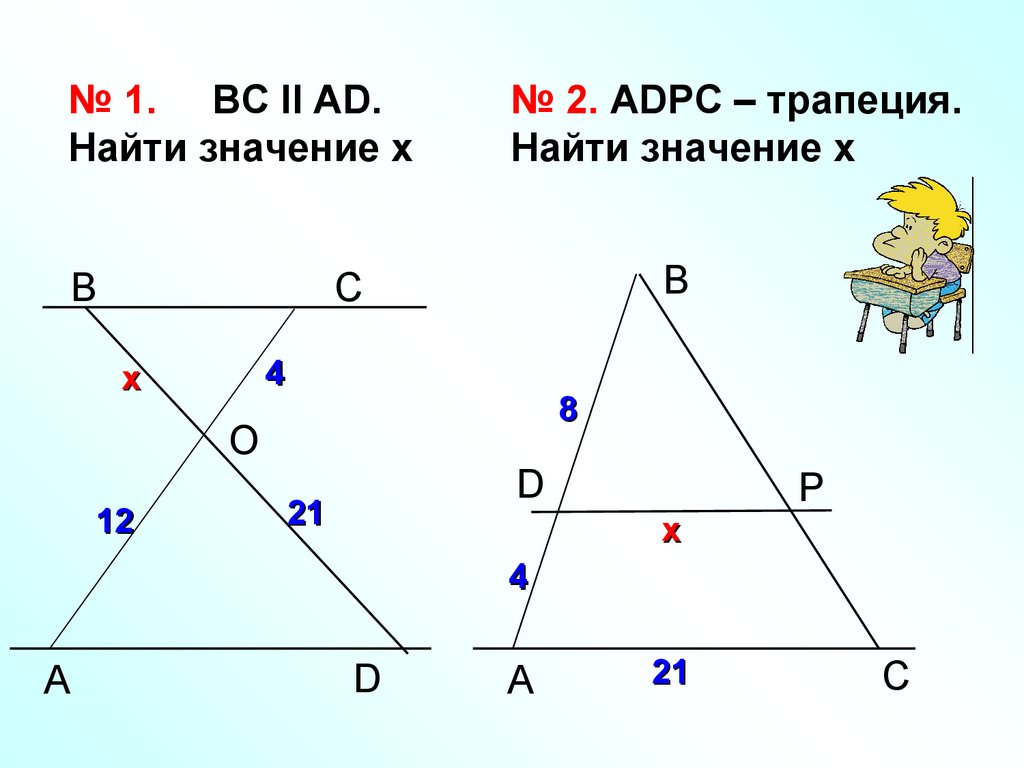
№ 1. BC II AD.Найти значение х
B
№ 2. ADPC – трапеция.
Найти значение х
B
С
4
x
8
O
12
D
21
P
x
4
A
D
A
21
C
3.
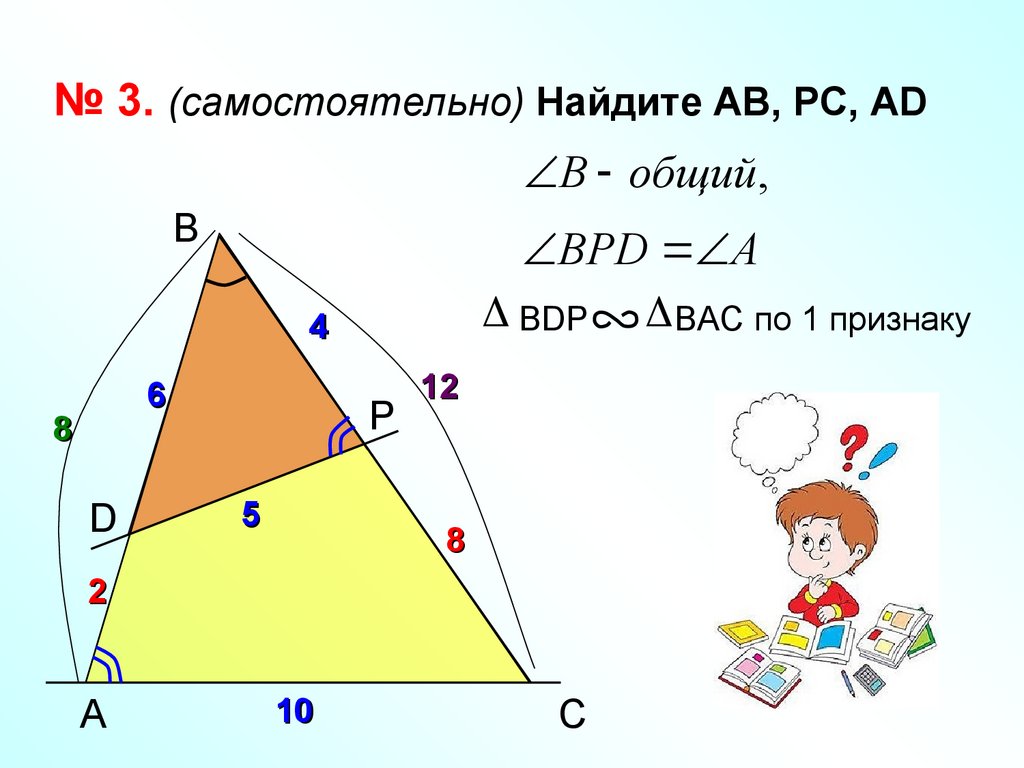
№ 3. (самостоятельно) Найдите АВ, РС, АDВ общий,
B
ВРD A
BDP BAC по 1 признаку
4
6
8
D
P
5
12
8
2
A
10
C
4.
5.
Если две стороны одного треугольникапропорциональны двум сторонам другого
треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники подобны.
АВ
АС
Дано: ABC, А1В1С1, А А1 ,
А1 В1 А1С1
Доказать:
ABC
Доказательство:
А1В1С1
Самостоятельно (стр. 142)
С1
А1
С
В1
А
В
6.
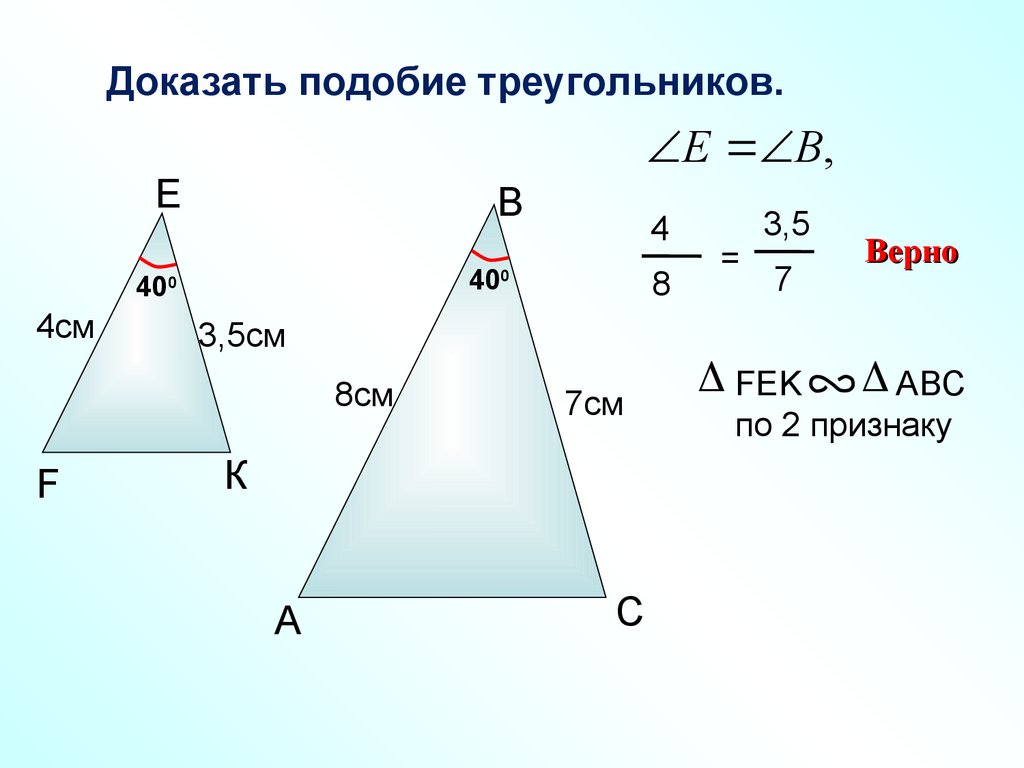
Доказать подобие треугольников.Е В,
Е
B
400
400
4см
8
=
3,5
7
Верно
3,5см
8см
F
4
7см
К
A
С
FEK
AВС
по 2 признаку
7.
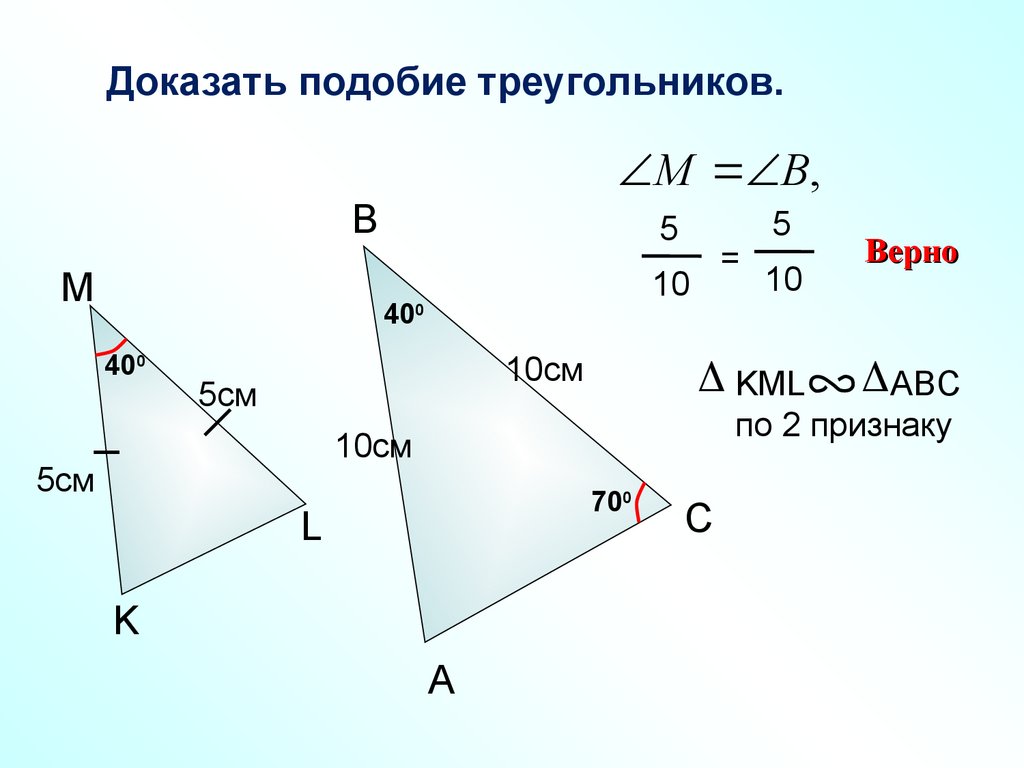
Доказать подобие треугольников.М В,
B
M
5
10
400
400
=
10см
5см
10
KML
Верно
ABC
по 2 признаку
10см
5см
5
700
L
K
A
C
8.
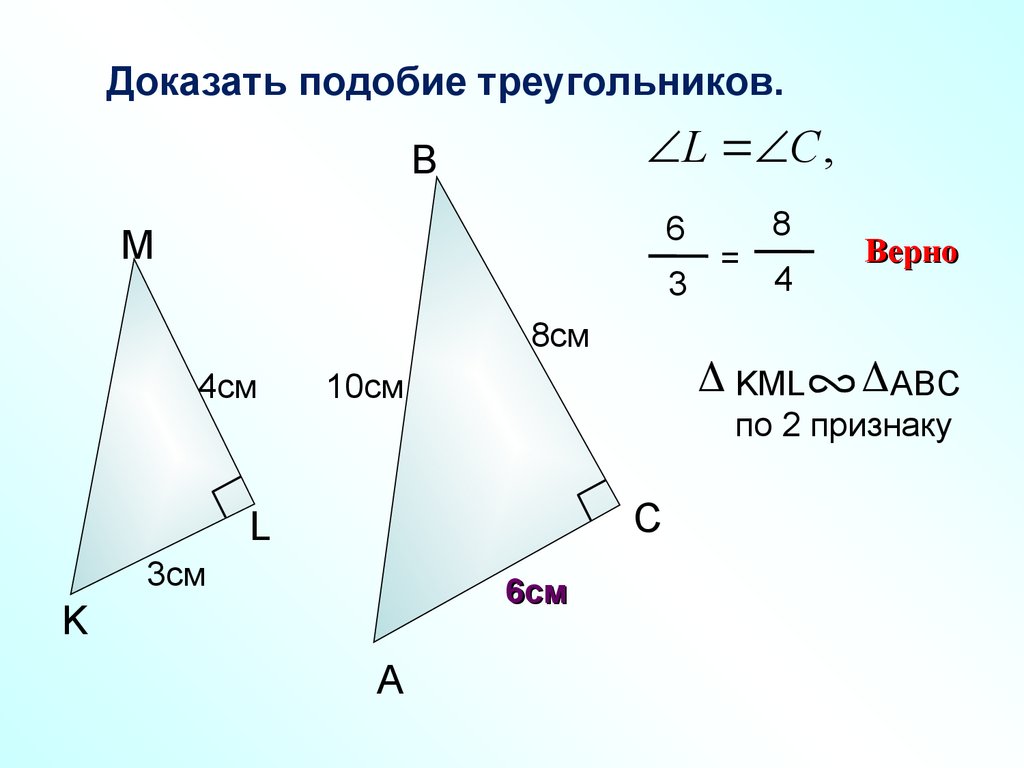
Доказать подобие треугольников.L C ,
B
6
M
3
=
8
4
Верно
8см
4см
KML
10см
ABC
по 2 признаку
C
L
3см
6см
K
A
9.
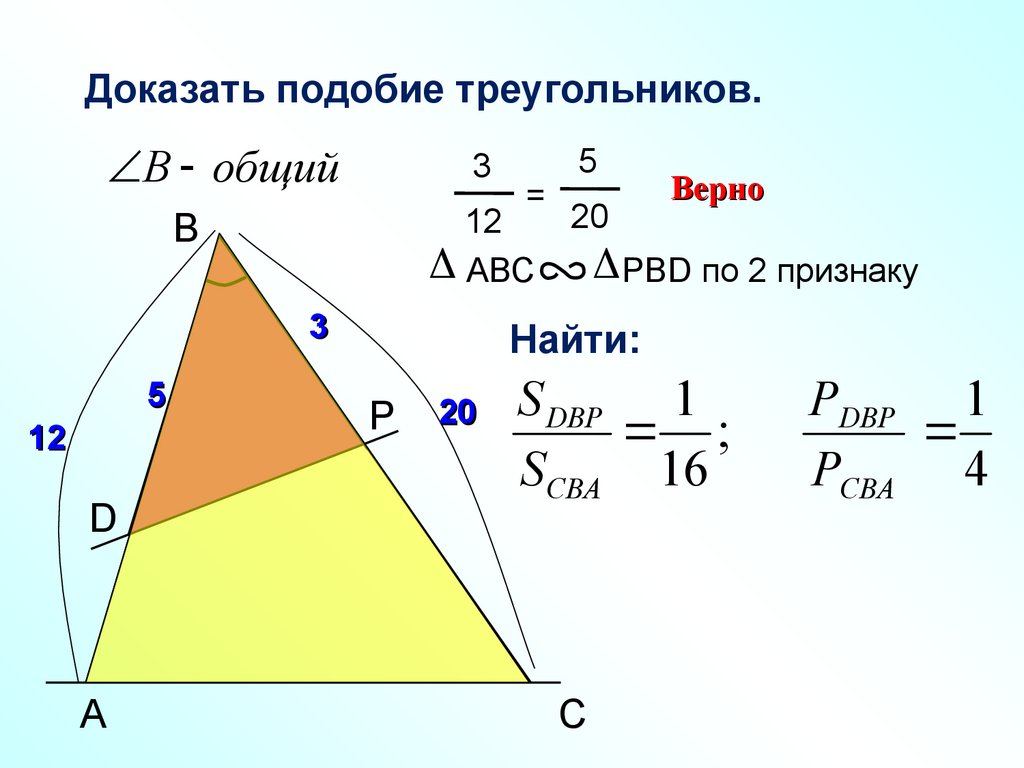
Доказать подобие треугольников.В общий
3
12
AВС
B
3
5
12
D
A
=
5
20
Верно
РВD по 2 признаку
Найти:
P
20
S DBP 1
;
SCBA 16
C
РDBP 1
РCBA 4
10.
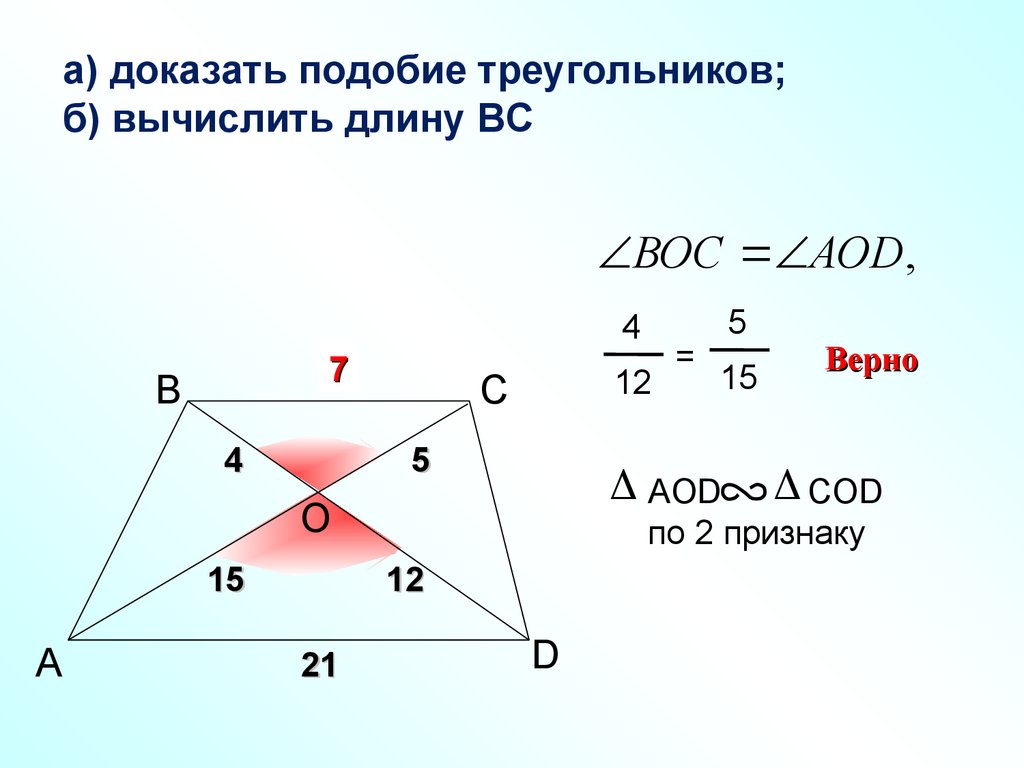
а) доказать подобие треугольников;б) вычислить длину ВС
ВОС АОD ,
4
?
7
B
4
12
С
5
A
Верно
COD
по 2 признаку
12
21
15
AОD
O
15
=
5
D
11.
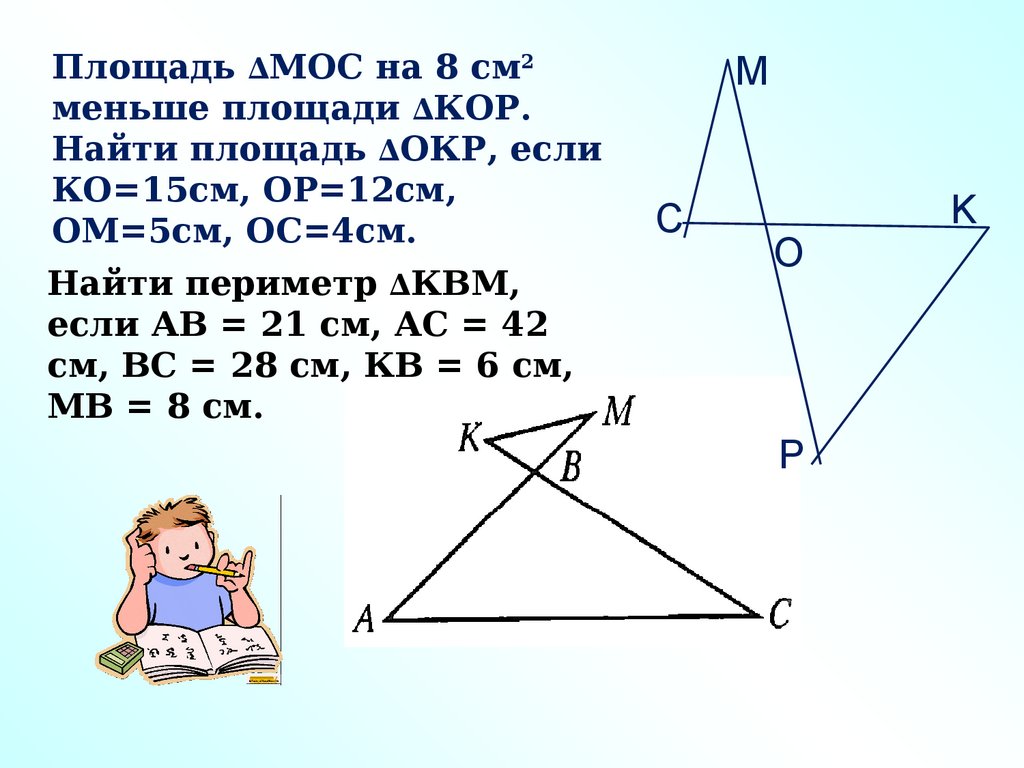
Площадь ∆МОС на 8 см2меньше площади ∆КОР.
Найти площадь ∆ОКР, если
КО=15см, ОР=12см,
ОМ=5см, ОС=4см.
Найти периметр ∆КВМ,
если АВ = 21 см, АС = 42
см, ВС = 28 см, КВ = 6 см,
МВ = 8 см.
M
C
О
P
K
12.
Домашнее заданиеТЕОРИЯ: стр. 142 – записать
доказательство теоремы о
II признаке подобия
треугольников в словарь,
выучить;
ЗАДАЧИ: решить № 549,
557, 559




 Математика
Математика








