Похожие презентации:
Выразить переменную из формулы. Подготовка к ЕГЭ
1.
Выразить переменную изформулы
Дудников Ю. А.
МБОУ Качалинская СОШ
2017
2.
Порядок выражения переменной1. В той части формулы, где содержится переменная, которую
нужно выразить, расставьте порядок действий. В одночленах и
многочленах, не содержащих искомую величину, порядок
действий не расставляем.
2. Найдите в выражении последнее действие, и перенести
одночлен или многочлен, исполняющий это действие через
знак равенства первым, но уже с противоположным действием.
Таким образом, перенесите из одной части равенства в
другую все известные величины. В заключение перепишите
формулу так, чтобы неизвестная переменная стояла слева.
3.
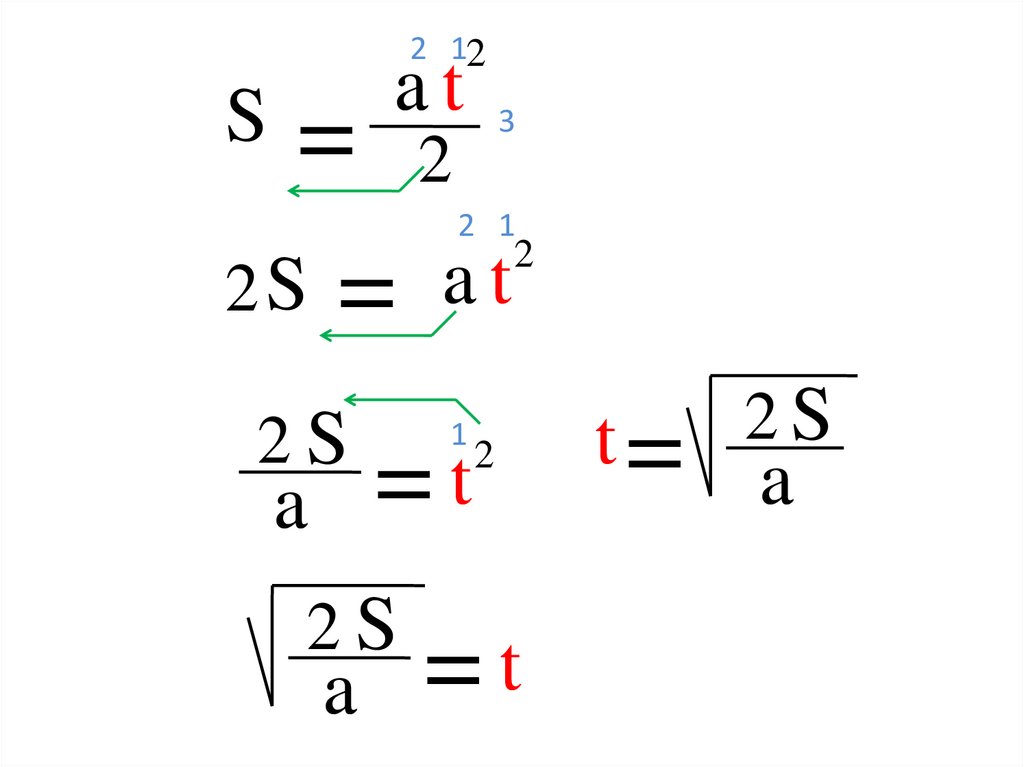
2 12S=
at 3
2
2 1
2S = a t
2S
1
t
=
a
2S
2
2
t
=
a
t=
2S
a
4.
υυ
2
a=
1
t
0
a t = υ -υ
1
0
a t+ υ = υ
0
υ= at + υ
0
5.
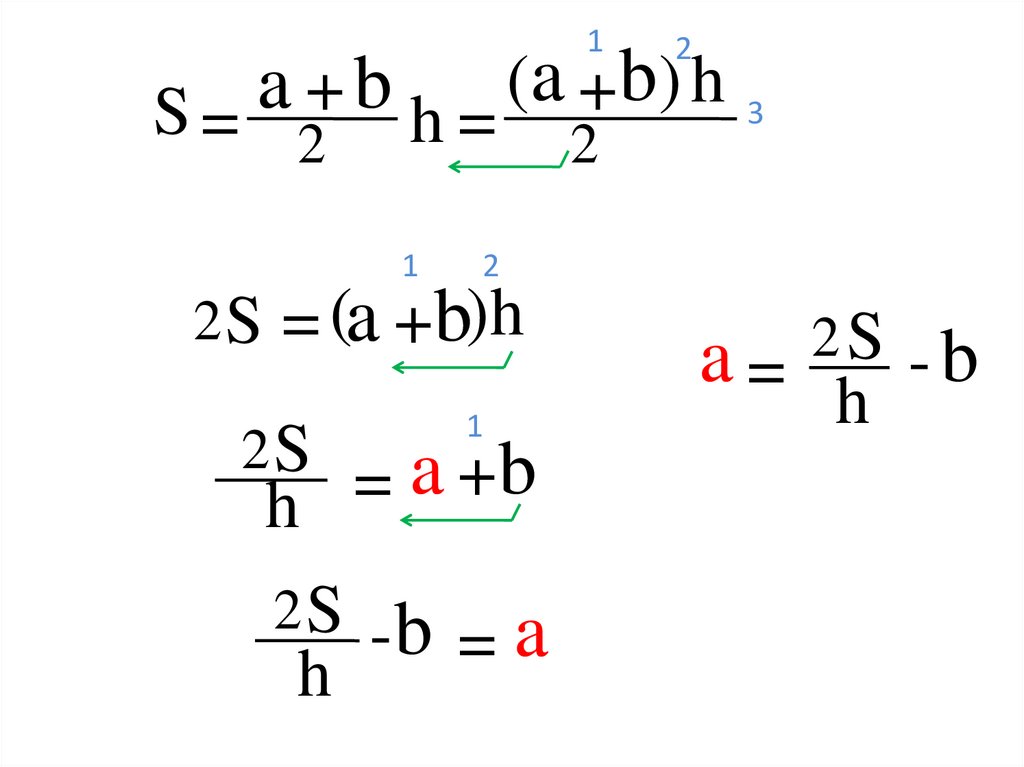
12
a
b
(
)
h
a
b
+
+
3
S=
h=
2
2
1
2
2 S = (a +b)h
2S
1
a
b
+
=
h
2 S -b
h
=a
a=
2S - b
h
6.
1υ
υ
a= t 2
0
at =υ-υ
1
0
Заново расставляем порядок действий, так как нужная
переменная оказалась в другой части формулы.
t =
υ-υ
0
a
7.
1(υ +υ ) t 3
υ
υ
+
S=
t=
0
0
2
2
1
2
2 S = (υ +υ0 )t
2S
t
S
2
υ=
- υ0
t
1
= υ +υ
0
2 S - υ0 = υ
t
2
8.
21
Q = m c (t - t )
к
0
1
Q
-t
t
=
mc
Q +t = t
mc
к
0
0
к
Q +t
t = mc
к
0
9.
-υ 3υ
S = 2a
12 2
2
0
2 aS = υ - υ0
1 22
2
2a S + υ 0 = υ
12
2
2a S + υ 0
2
υ = 2a S + υ
=υ
2
0
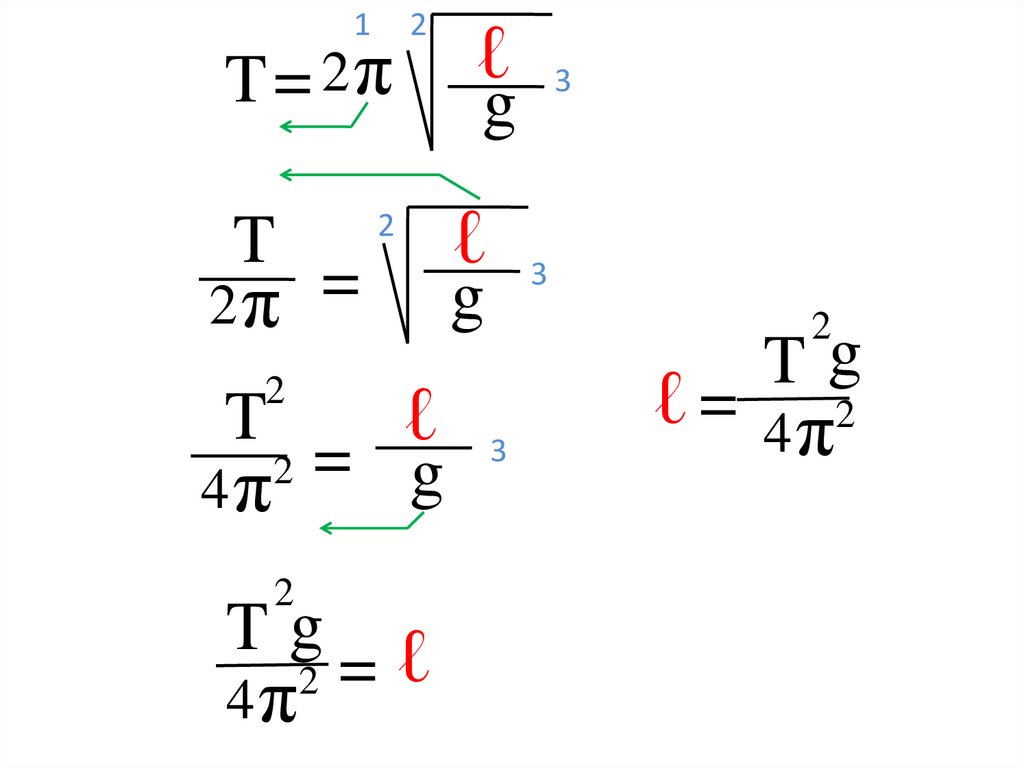
10.
1T = 2π
2
g
ℓ 3
2
T
=
2π
ℓ 3
g
ℓ 3
2
T
=
g
4π
2
2
Tg
ℓ
=
4π
2
2
Tg
ℓ = 4 π2
11.
21hν = hν + mυ 3
4
кр
2
2
2 12
hν - hν = mυ 3
кр
2
2 12
2( h ν - h νкр) = m υ
2( h ν - h νкр)
m
=υ
2( h ν - h νкр)
m
12
=υ
υ=
2( h ν - h νкр)
m
12.
н - TхT
η=
1
Тн
Тн η = Tн - Tх
Тн η -Tн = -Tх
Тн (η -1) = - Tх
T
T = η-1
н
х
х
T
Tн = 1 η
-
13.
d2
C=
d- k
C (d-k) = 2 - d
C d - C k= 2 - d
C d + d = 2+ C k
d(C +1) = 2 + C k
2
+
k
C
d= C+ 1
14.
1(υ +υ ) t 3
υ
+
υ
S=
t=
0
0
2
2
1
2
2 S = (υ +υ0 )t
2S
t
S
2
- υ0
υ=
t
1
= υ +υ
0
2 S -υ0 = υ
t
2
15.
41 22
x = t k +b
1+ a
5
3
4
1 22
x -b = t k
1+ a
2
2
(x - b) = t k
1+ a
1
2
1 2
2
2
3
2
3
(x-b) (1+a) = t k
2
(x-b) (1+a) 2
=t
k
1
(x-b) (1+a)
t=
k
16.
KE
m
+
K
E
m
+
4
S=
=
2
1
3
2
a x2 - b
(a x - b)
4 2 1 3
2
- b) = K E+ m
(
ax
S
2 1 23
m
K
E
+
ax -b =
x = K E + m + Sb
S
Sa
m
K
E
+
ax =
+b = K E + m + Sb
S
S
2 12
x = K E + m + Sb
Sa
12
17.
GM
g = ( + h)2
R
2
g(R+h) = G M
2 GM
(R+h) = g
G
M
R +h = g
G
M
h= g -R
18.
X=Asin(ω t +φ)X =sin(ω t +φ)
A
X
arcsin = ω t +φ
A
arcsin X -φ =ω t
A
1 arcsin X - φ
t= ω
A ω
19.
UX = δ β log 2
U0
X = log U
2
δβ
X
U = δβ
U0 2
U0
X
U = U0 2
δβ
20.
f0
f=
υ
1-
c
υ
f (1- c ) = f 0
f
0
υ
- =
1 c
f
f
υ
0
1- = c
f
f
0 c
υ = (1 - )
f


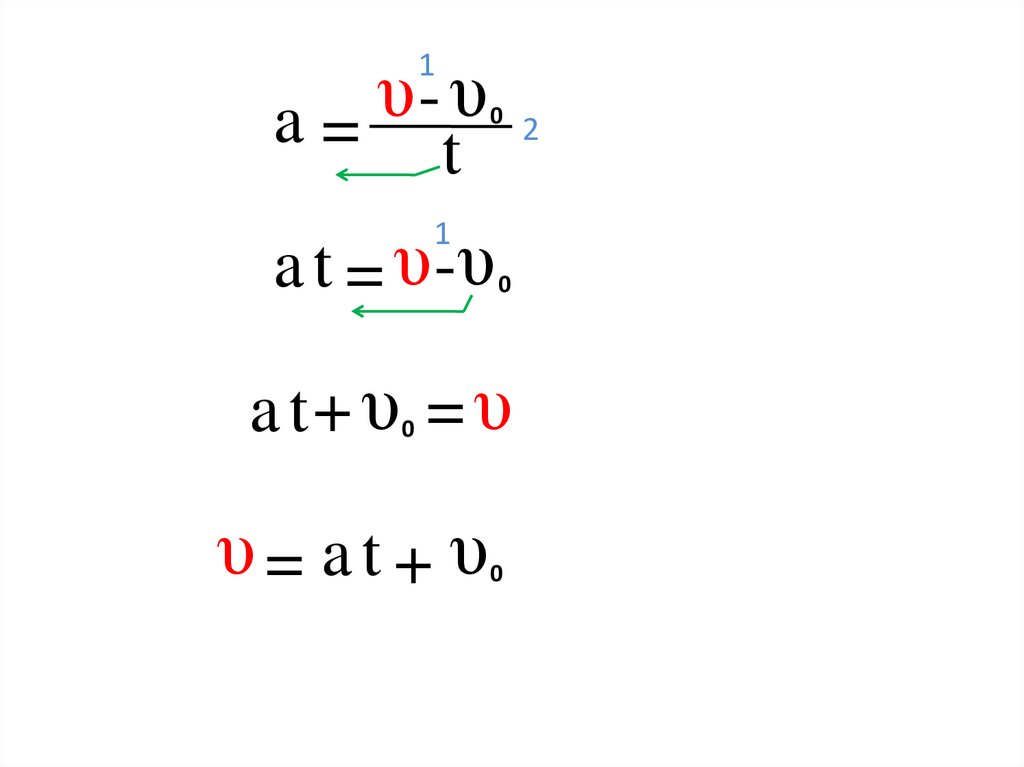

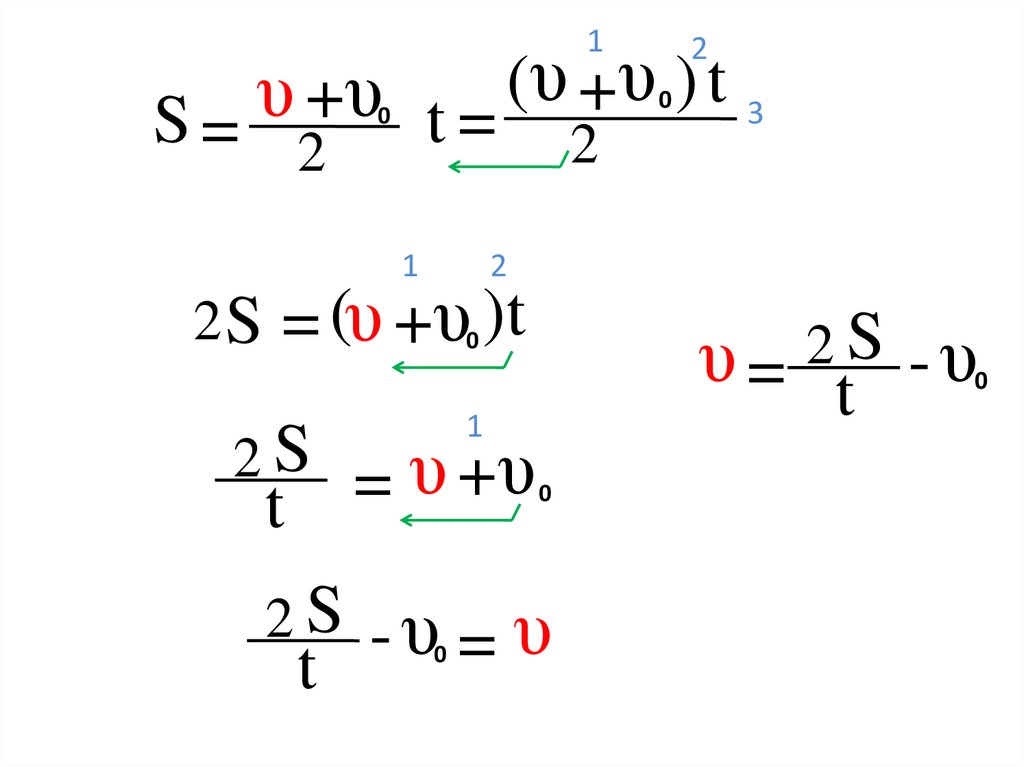
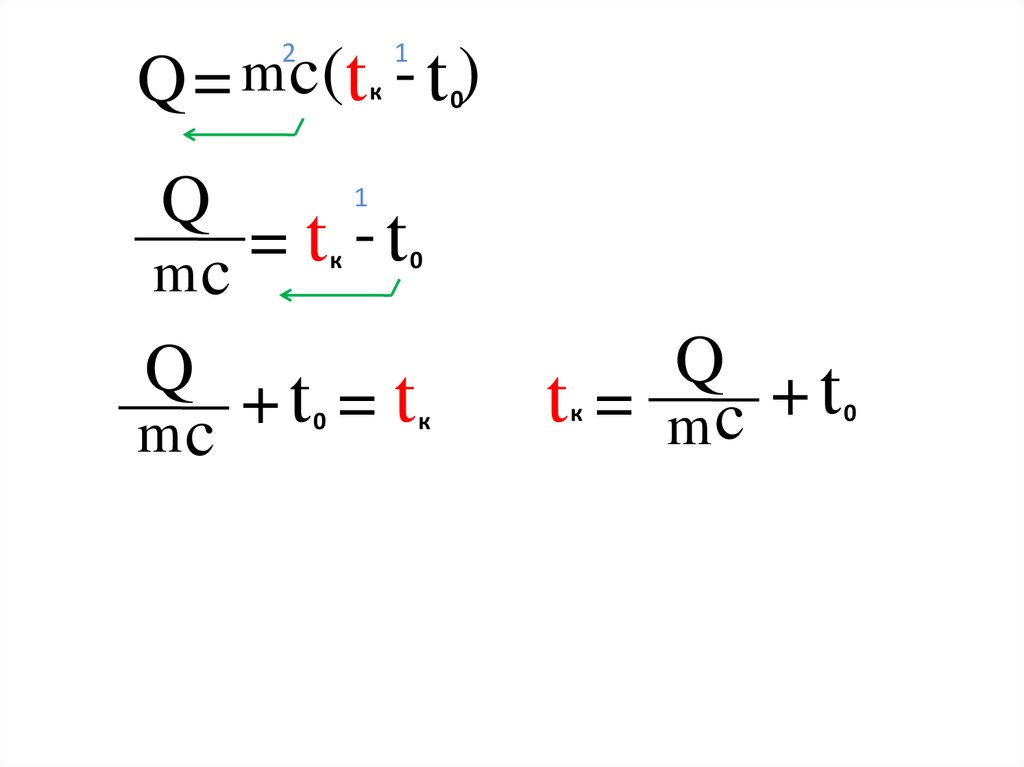
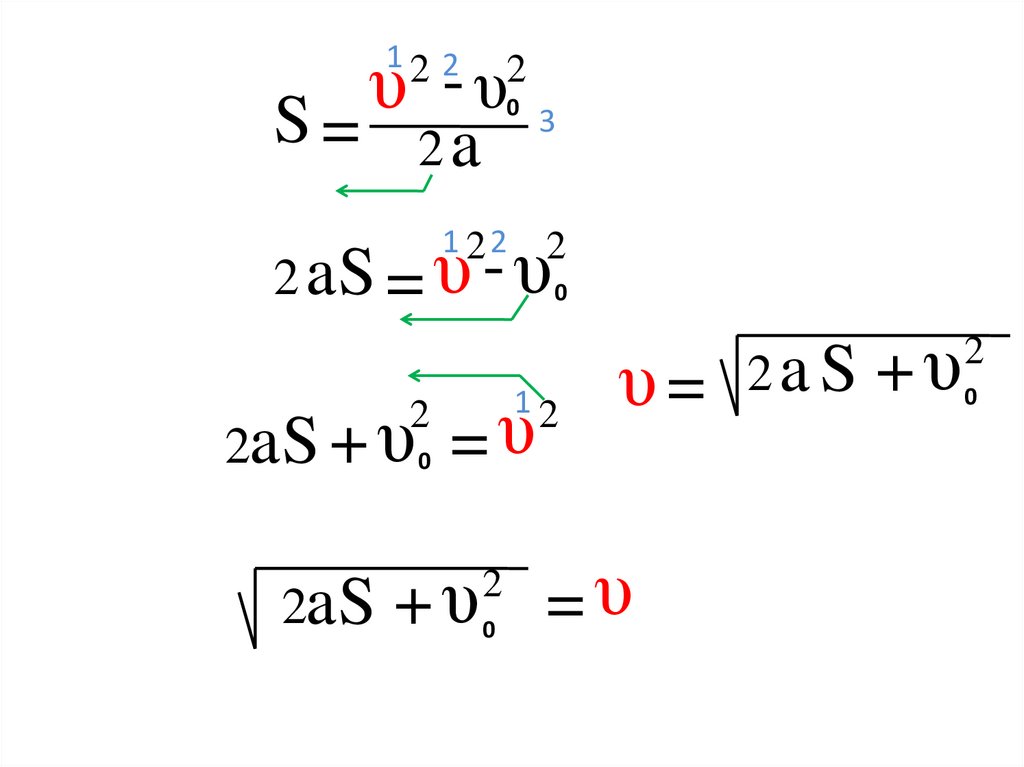
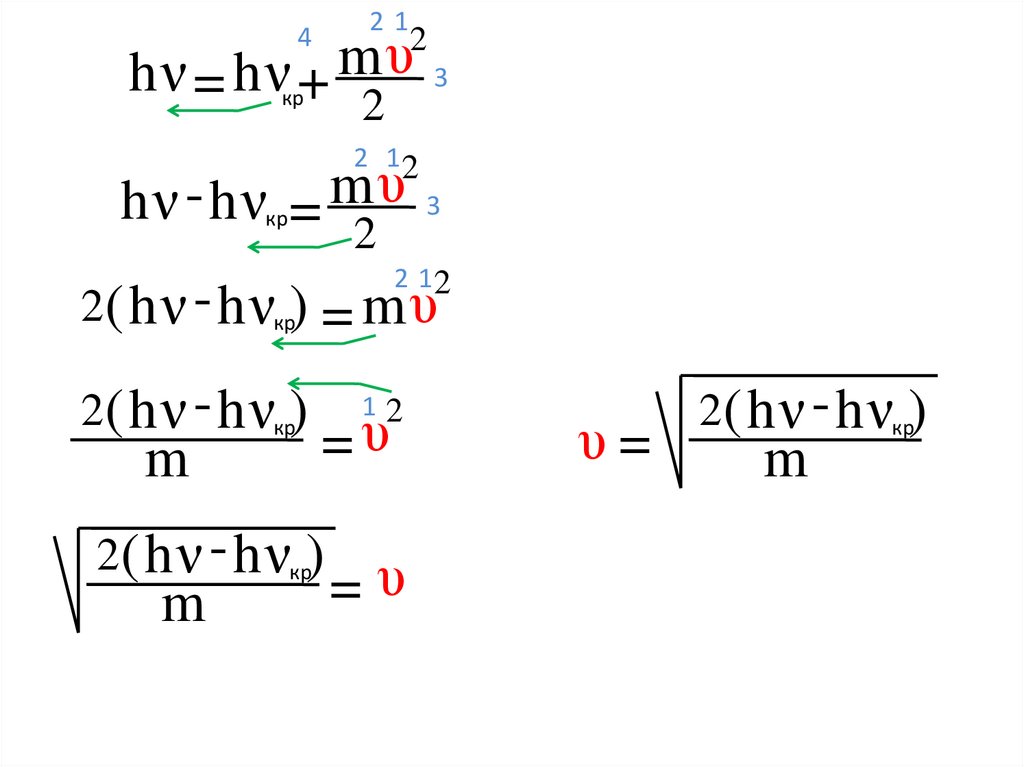
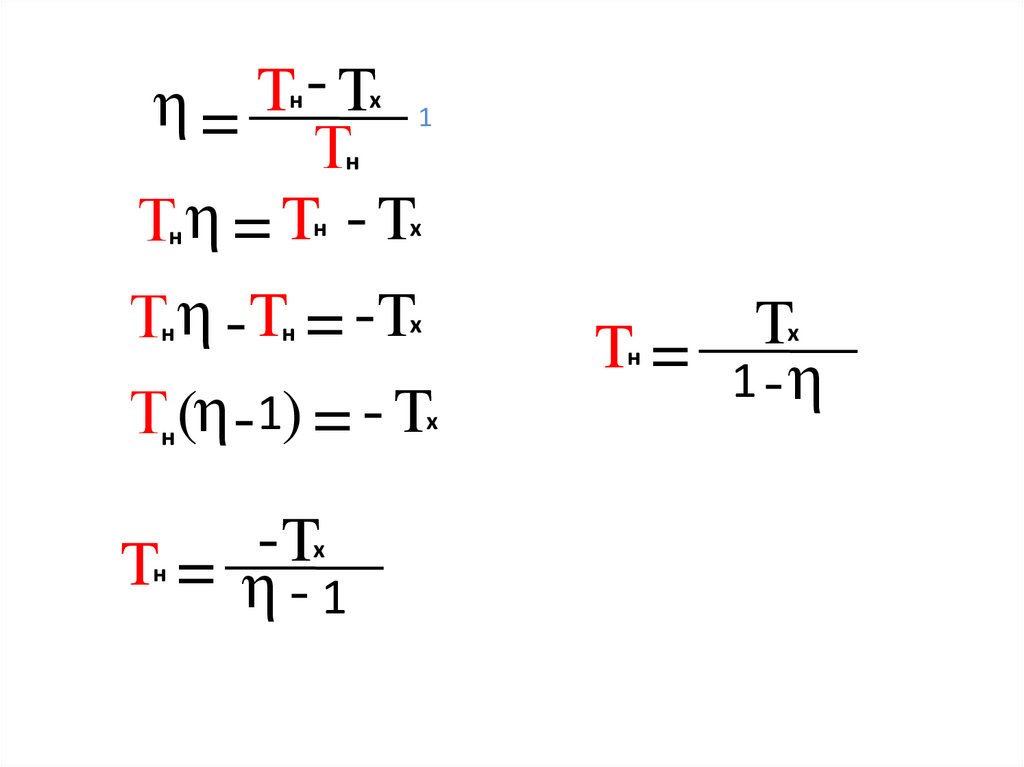
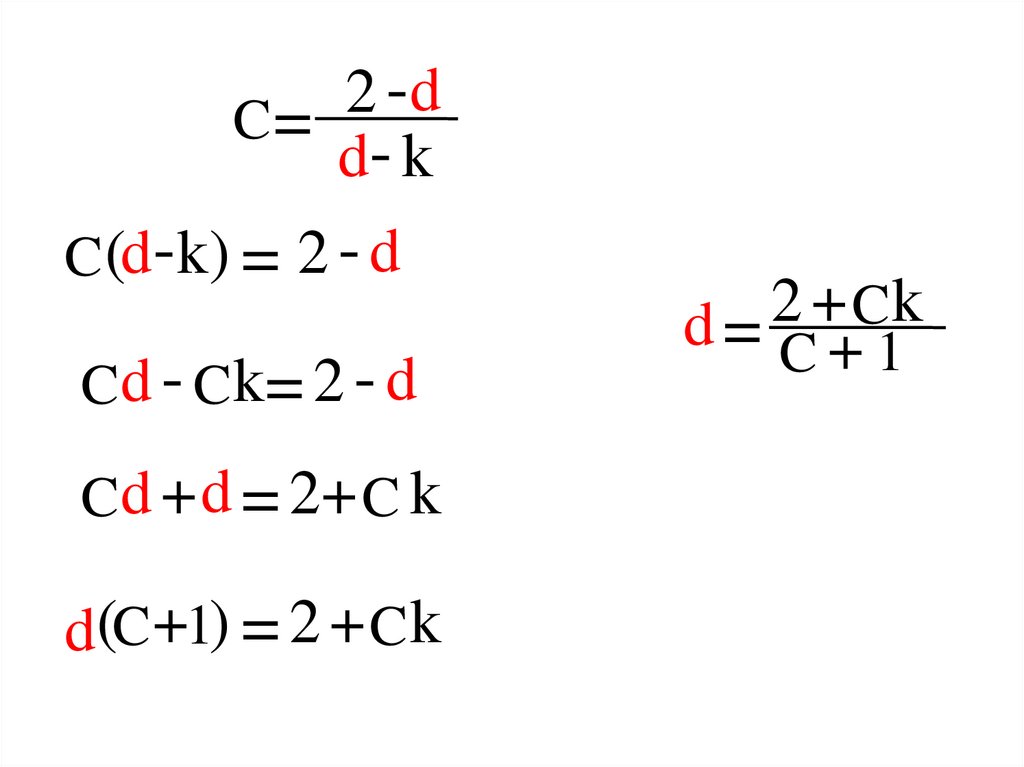
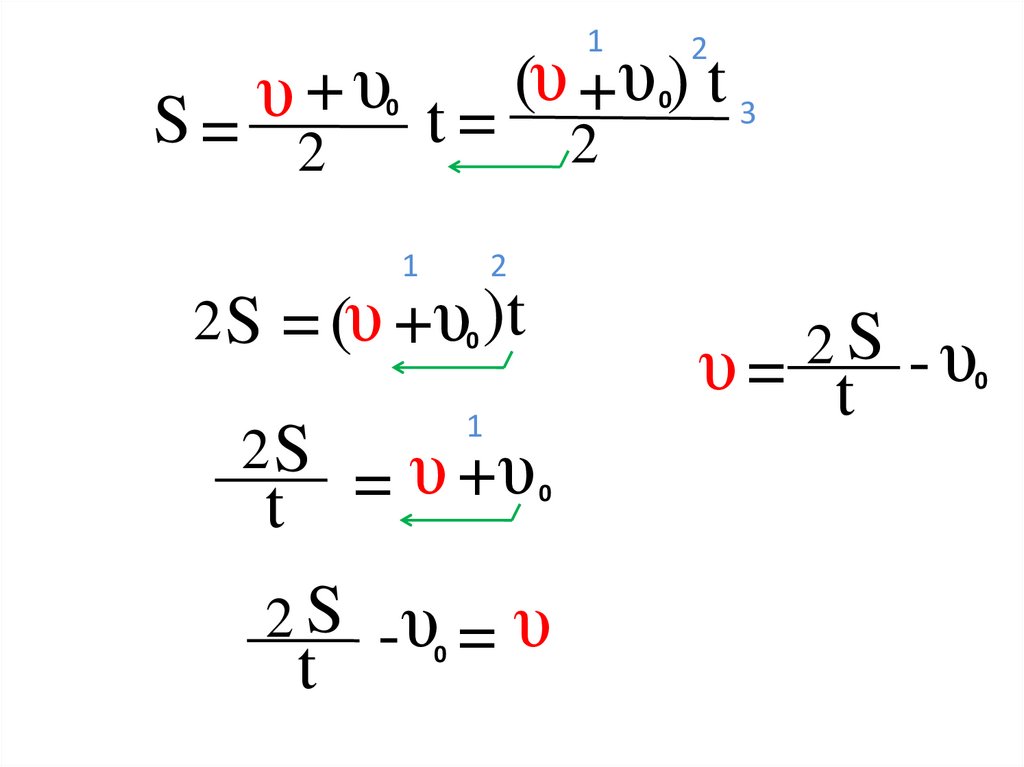
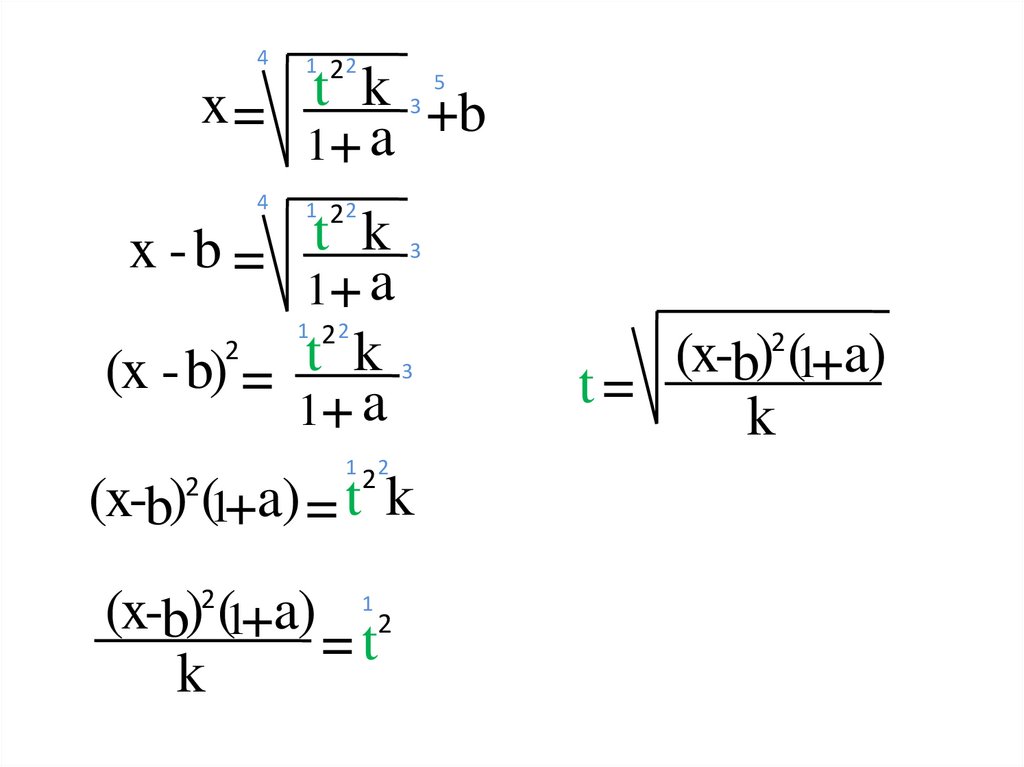
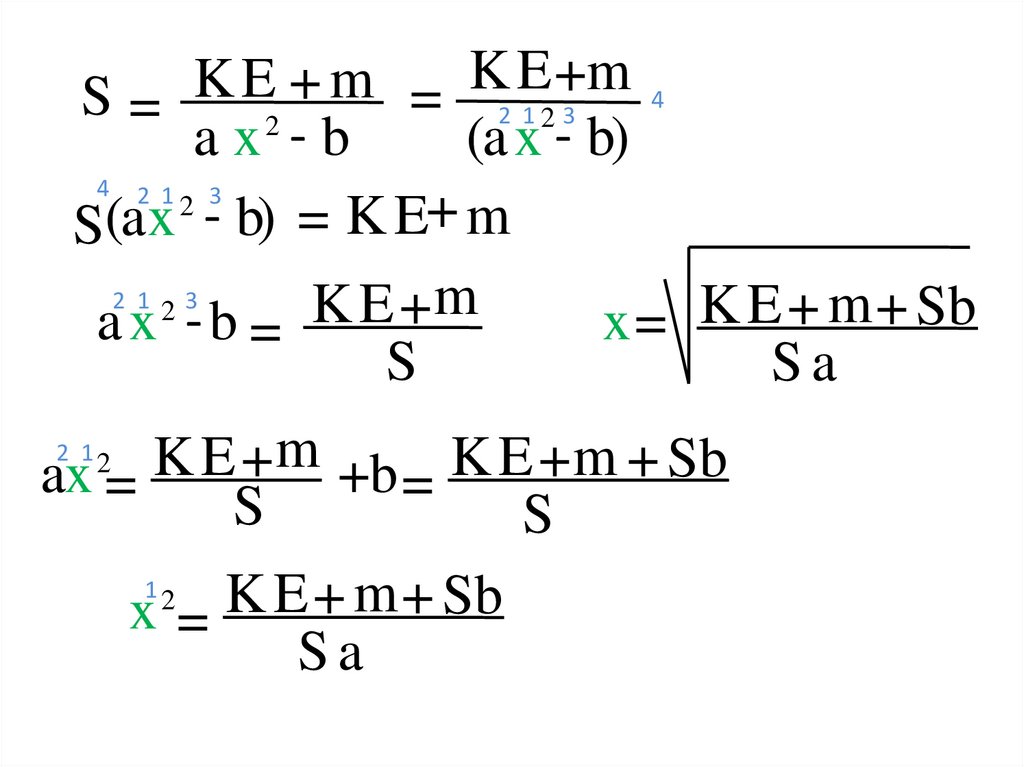
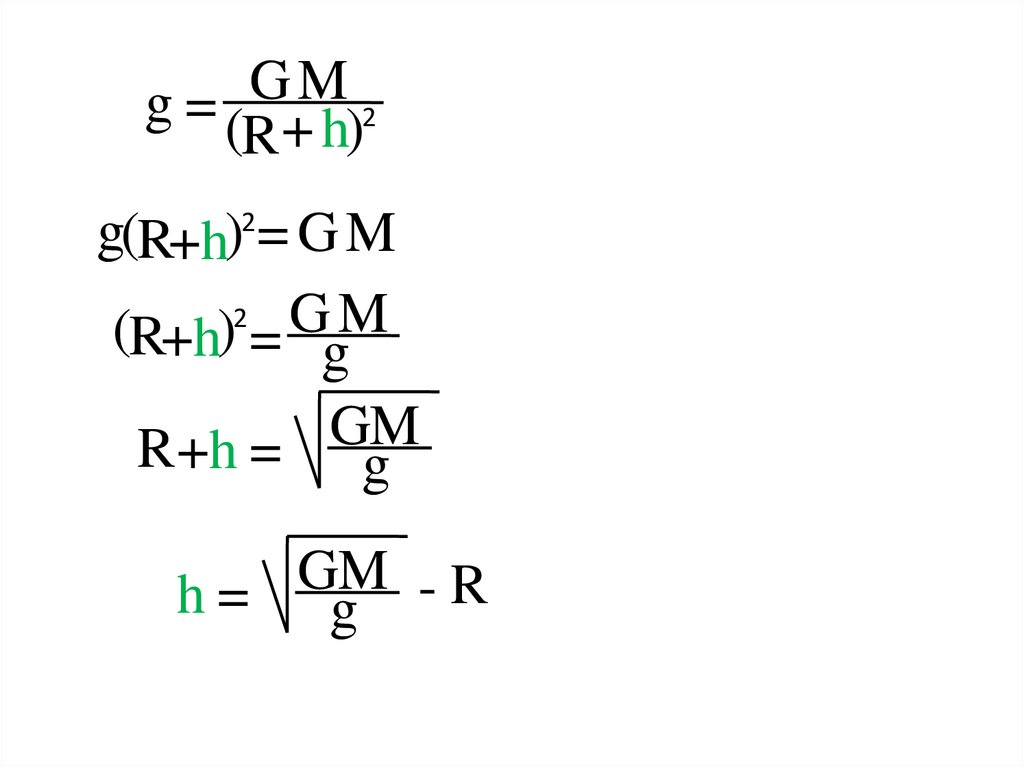
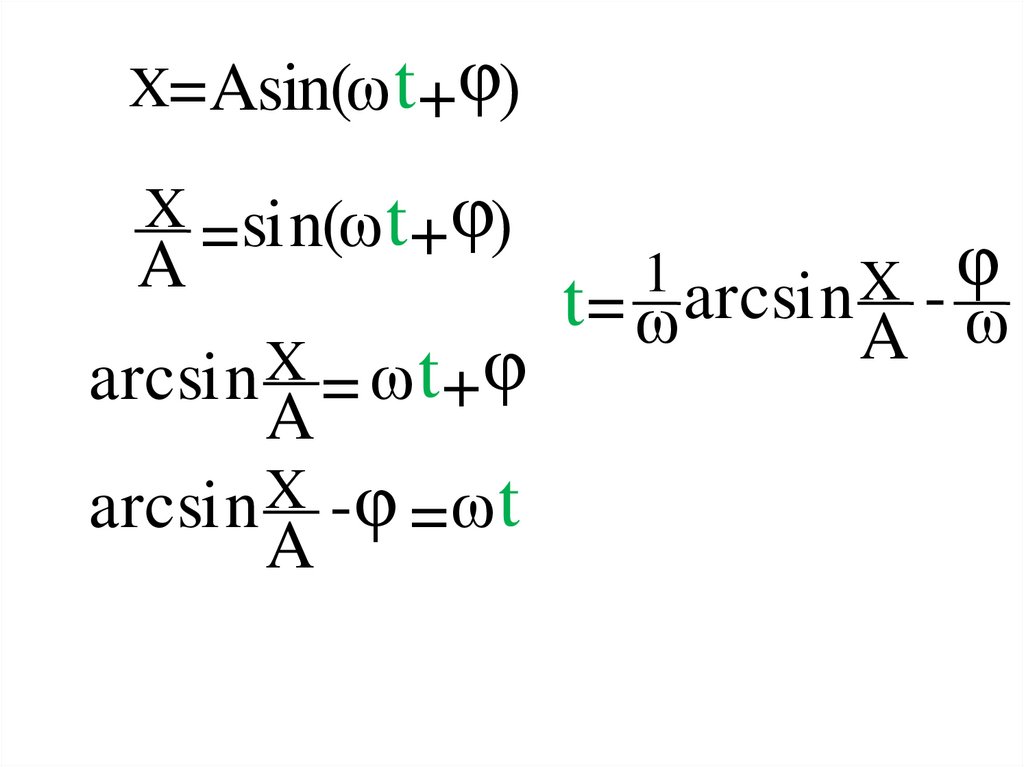
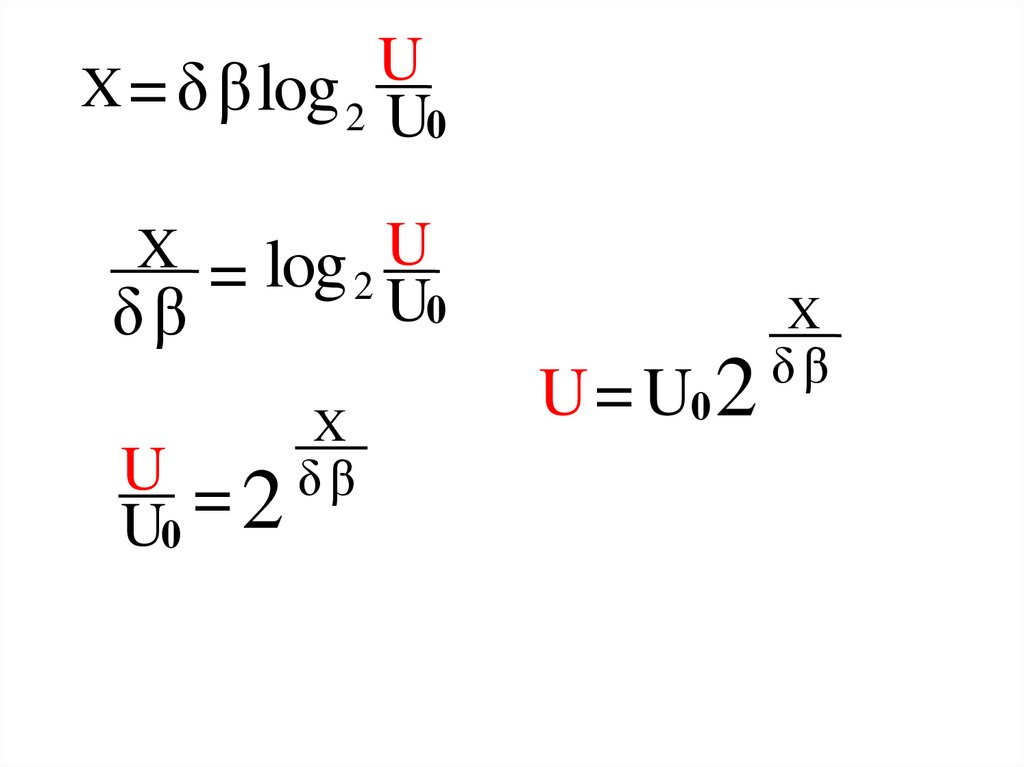
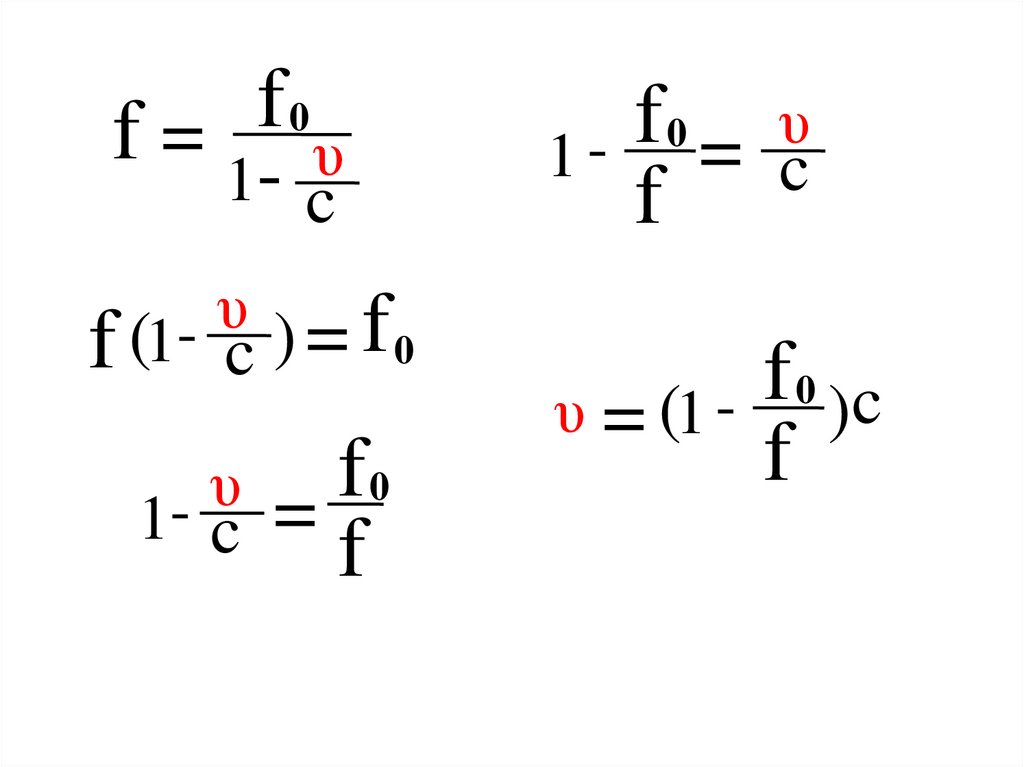
 Физика
Физика








