Геометрия приближает разум к истине

1. Выполнила презентацию: Учитель математики Кузнецова Алла Анатольевна МАОУ «СОШ с.Чапаево» 2019

Чему бы ты ни учился, ты учишься для
себя.
(Петроний- сатирик Древней Греции)

2. Приветствую вас на уроке геометрии в 8 классе

3.

Интересные
мысли и высказывания
Геометрия
приближает разум к истине
Платон
Успешного усвоения материала

4.

Отчёт
по выполнению
ДР в группе

5.

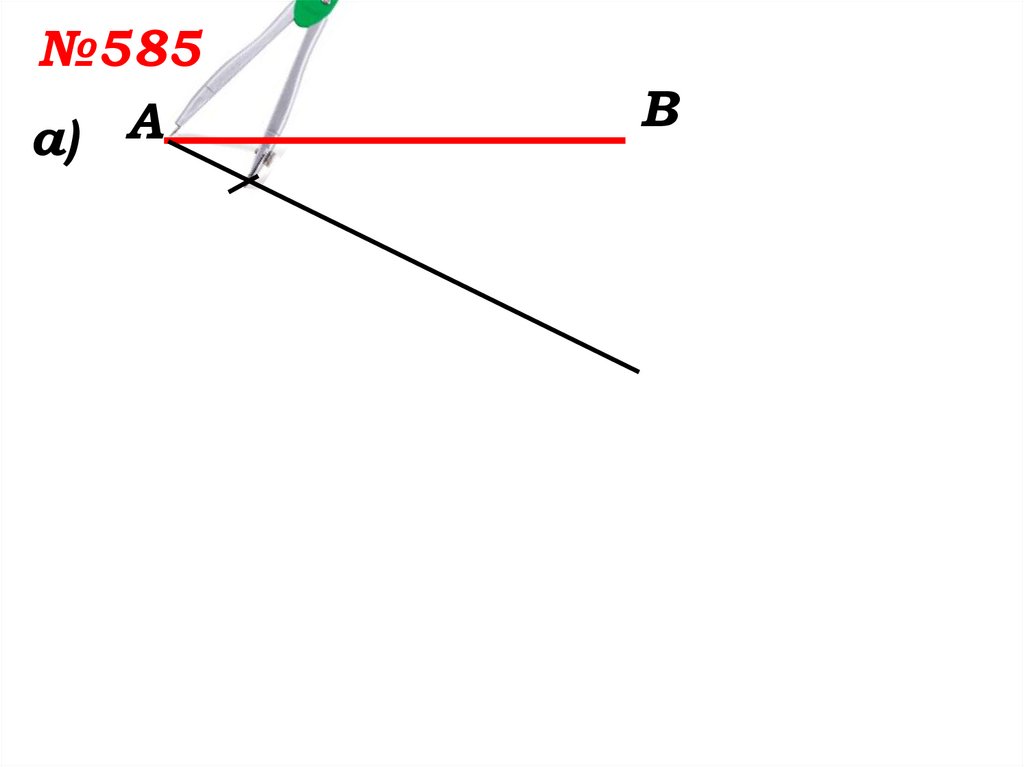
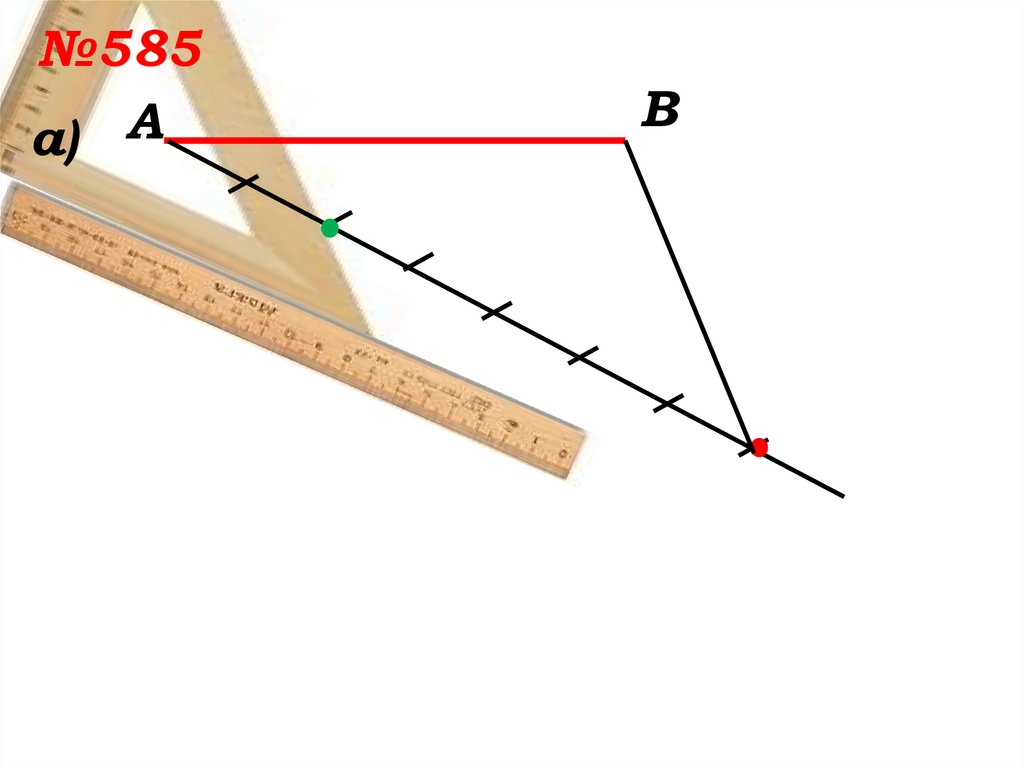
№585
а) А
В

6.

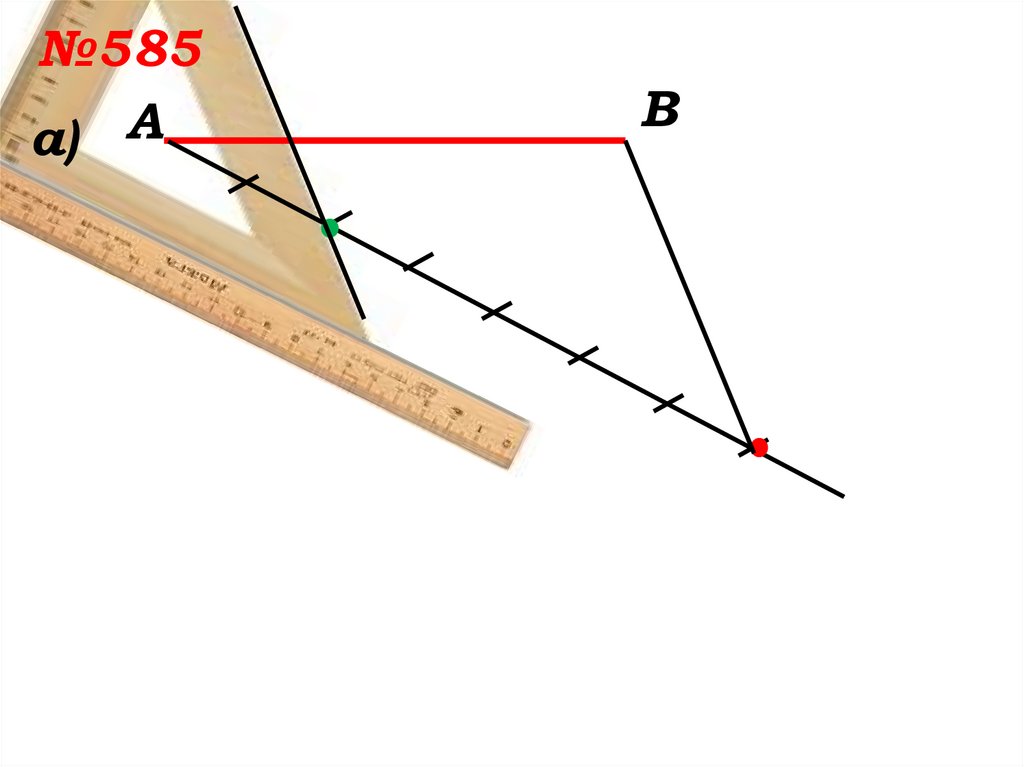
№585
а) А
В

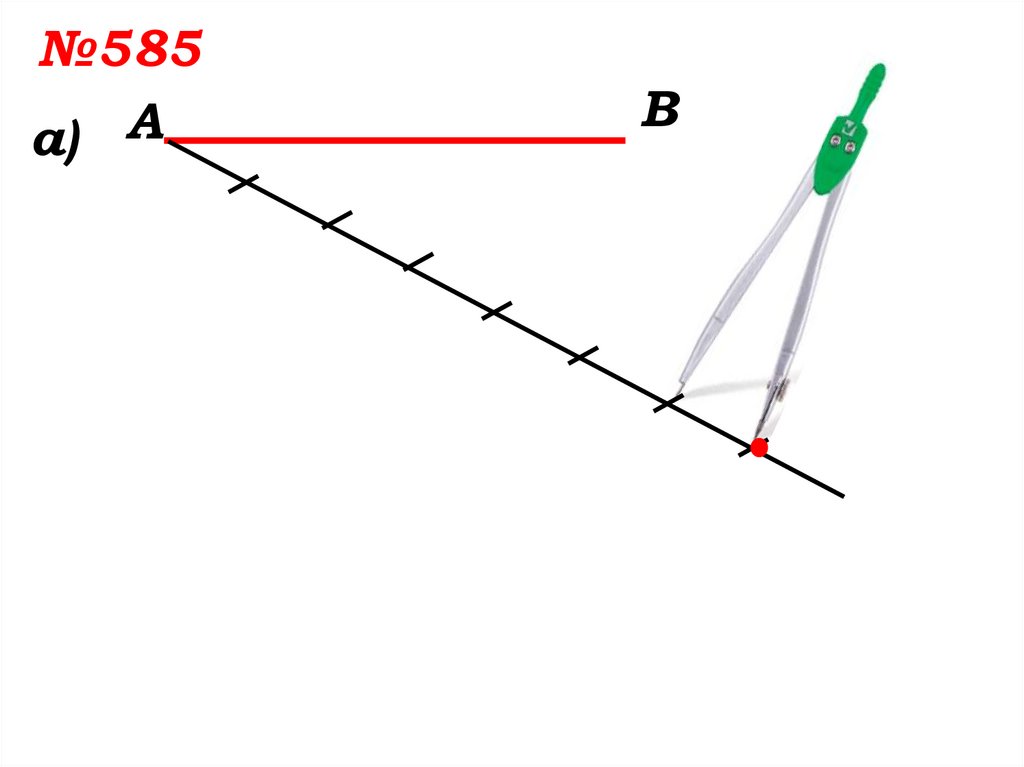
7.

№585
а) А
В

8.

№585
а) А
В

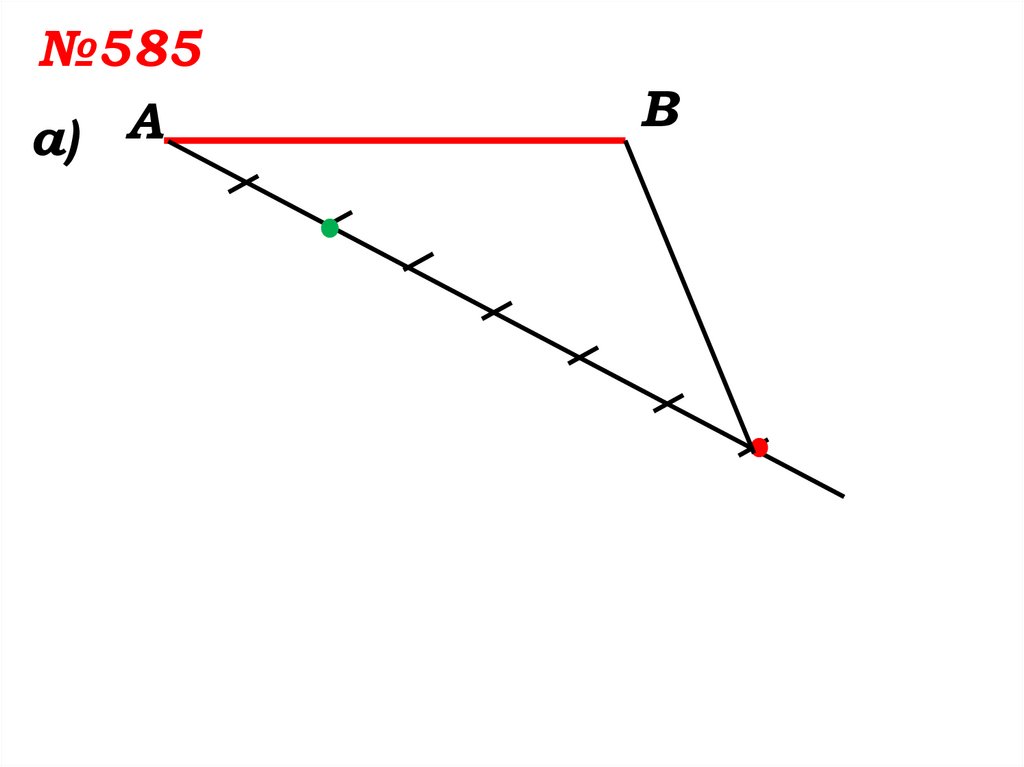
9.

№585
а) А
В

10.

№585
а) А
В

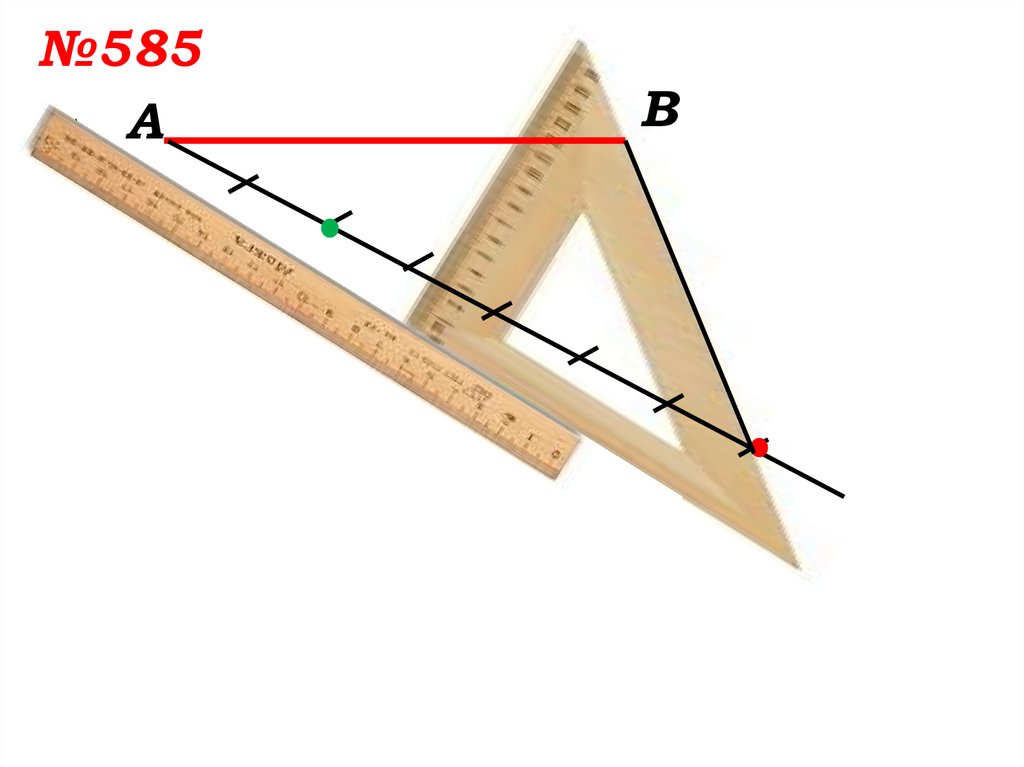
11.

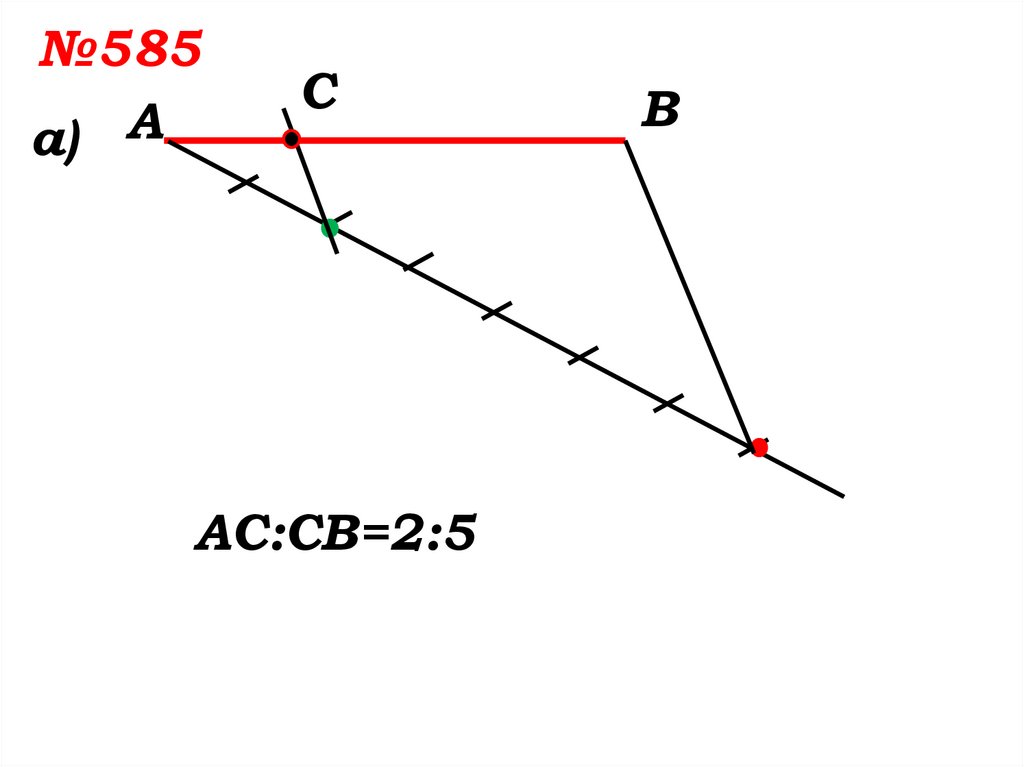
№585
а) А
С
АС:СВ=2:5
В

12.

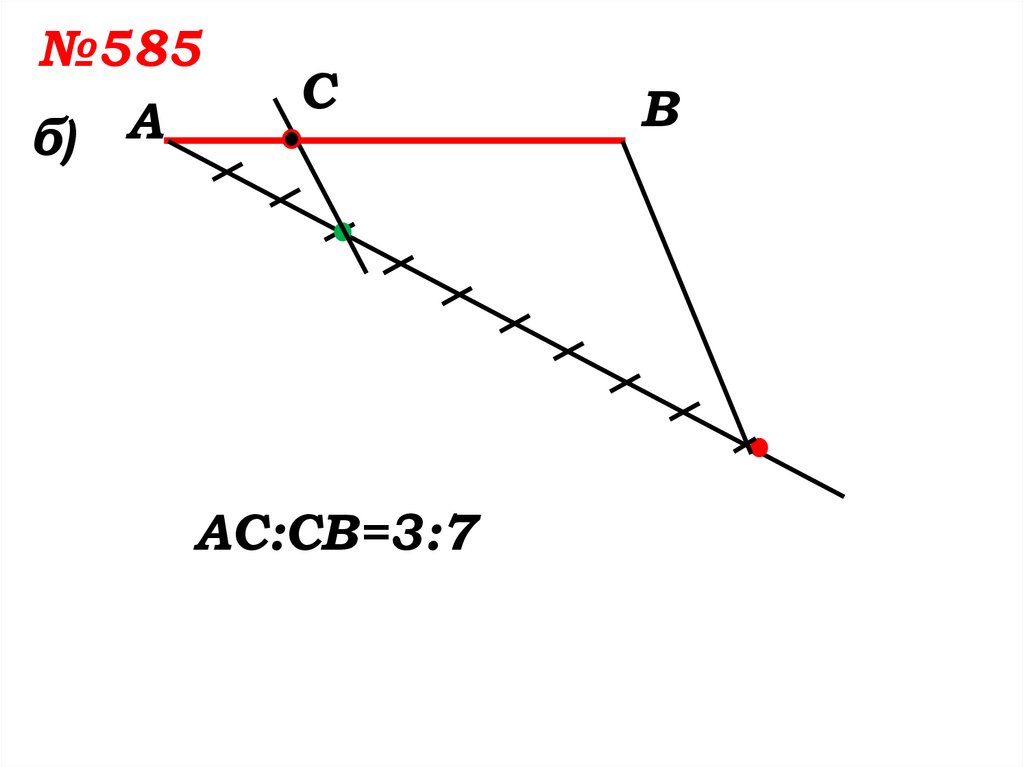
№585
б) А
С
АС:СВ=3:7
В

13.

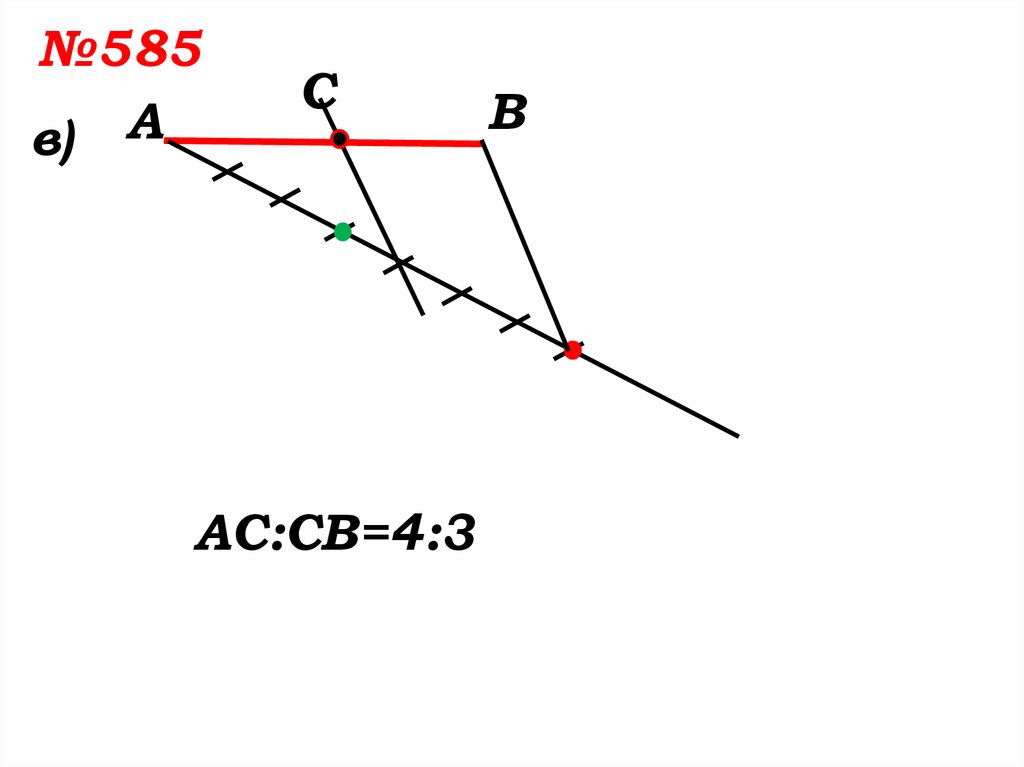
№585
в) А
С
АС:СВ=4:3
В

14.

Оцените ДР

15.

Соотношения между
сторонами и углами
прямоугольного треугольника

16.

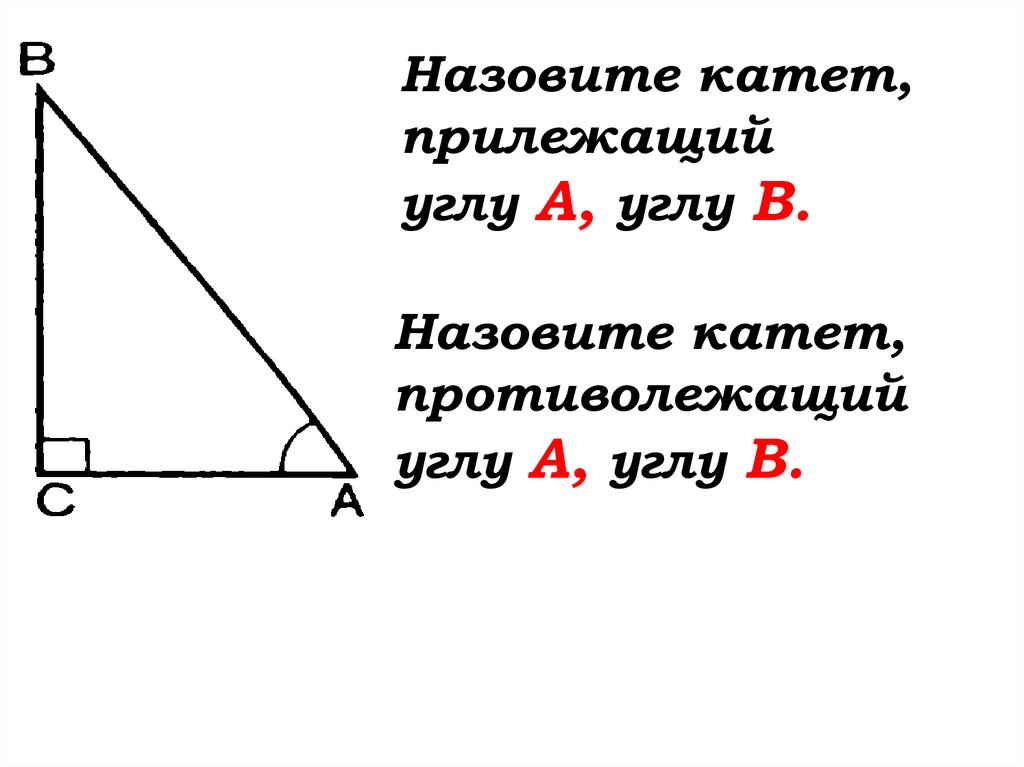
Назовите катет,
прилежащий
углу А, углу В.
Назовите катет,
противолежащий
углу А, углу В.

17.

Стр.156, п.66
Прочитайте определение
синуса острого угла
прямоугольного треугольника.
Что нужно знать, чтобы
указать чему будет равен
синус острого угла
прямоугольного треугольника?
sin синус угла

18.

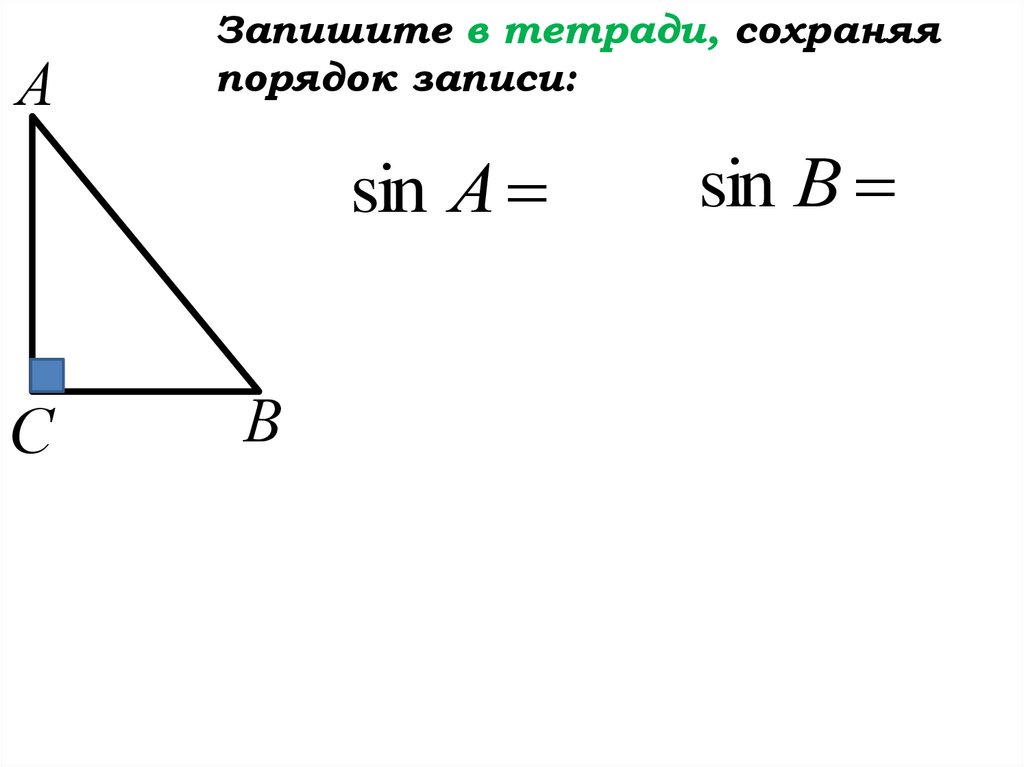
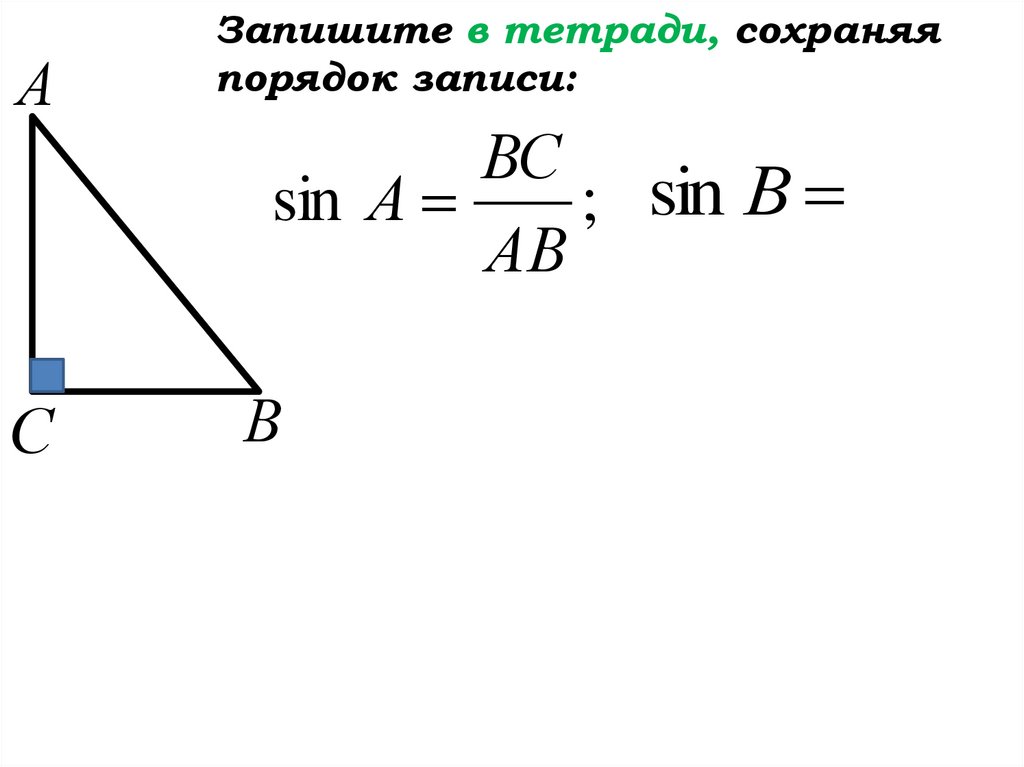
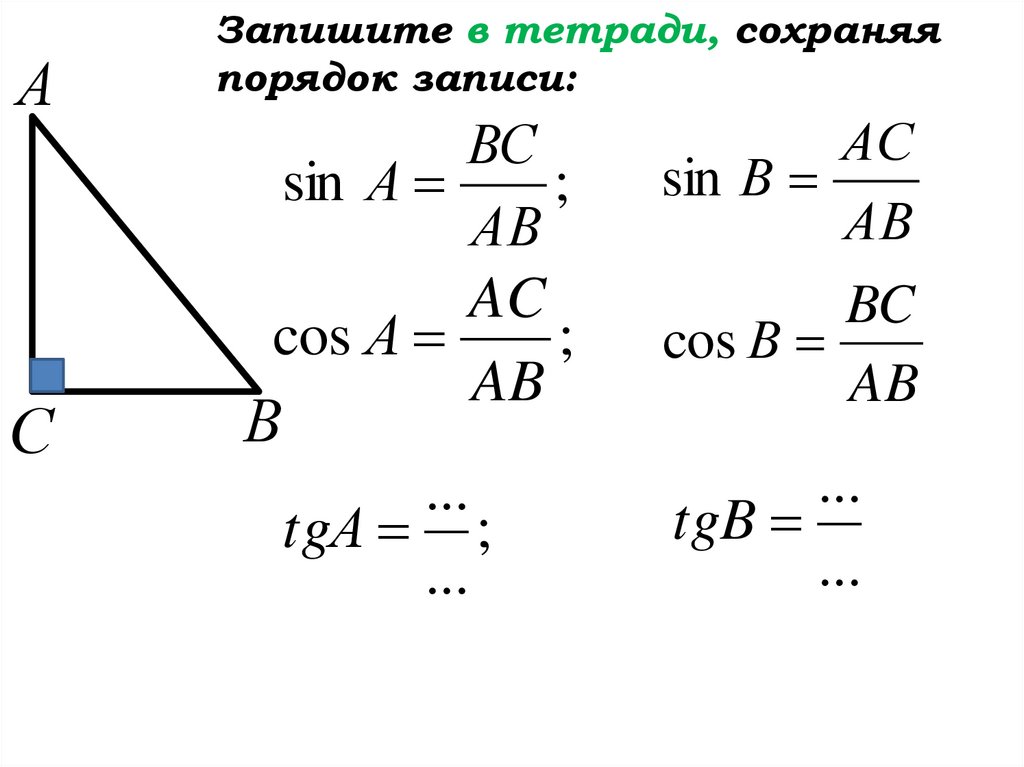
А
Запишите в тетради, сохраняя
порядок записи:
sin А
С
В
sin В

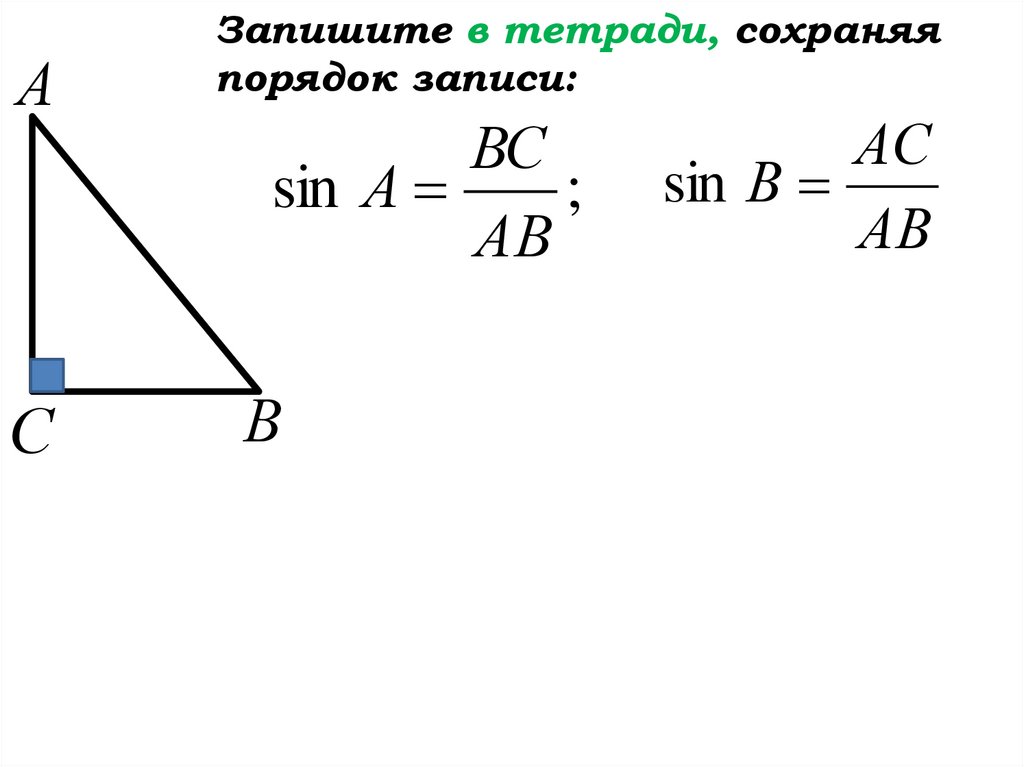
19.

А
Запишите в тетради, сохраняя
порядок записи:
ВС
sin А
; sin В
АВ
С
В

20.

А
С
Запишите в тетради, сохраняя
порядок записи:
ВС
sin А
;
АВ
В
АС
sin В
АВ

21.

Стр.156, п.66
Прочитайте определение
косинуса острого угла
прямоугольного треугольника.
Что нужно знать, чтобы
указать чему будет равен
косинус острого угла
прямоугольного треугольника?
соs косинус угла

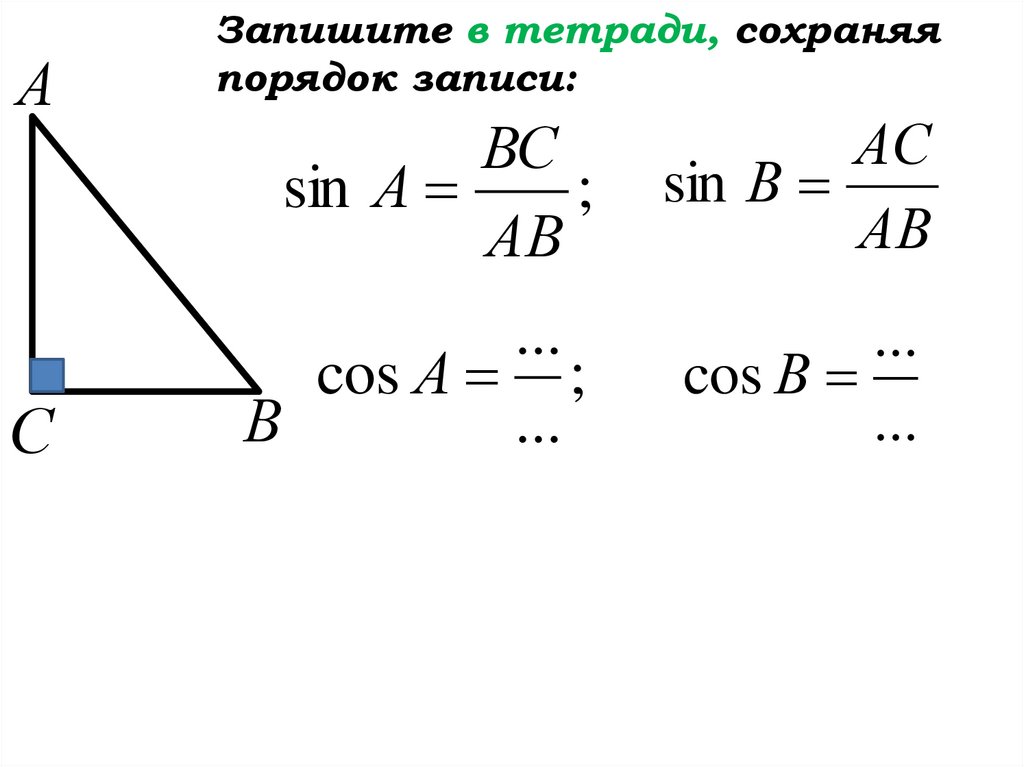
22.

А
С
Запишите в тетради, сохраняя
порядок записи:
ВС
sin А
;
АВ
АС
sin В
АВ
...
cos А ;
В
...
...
cos В
...

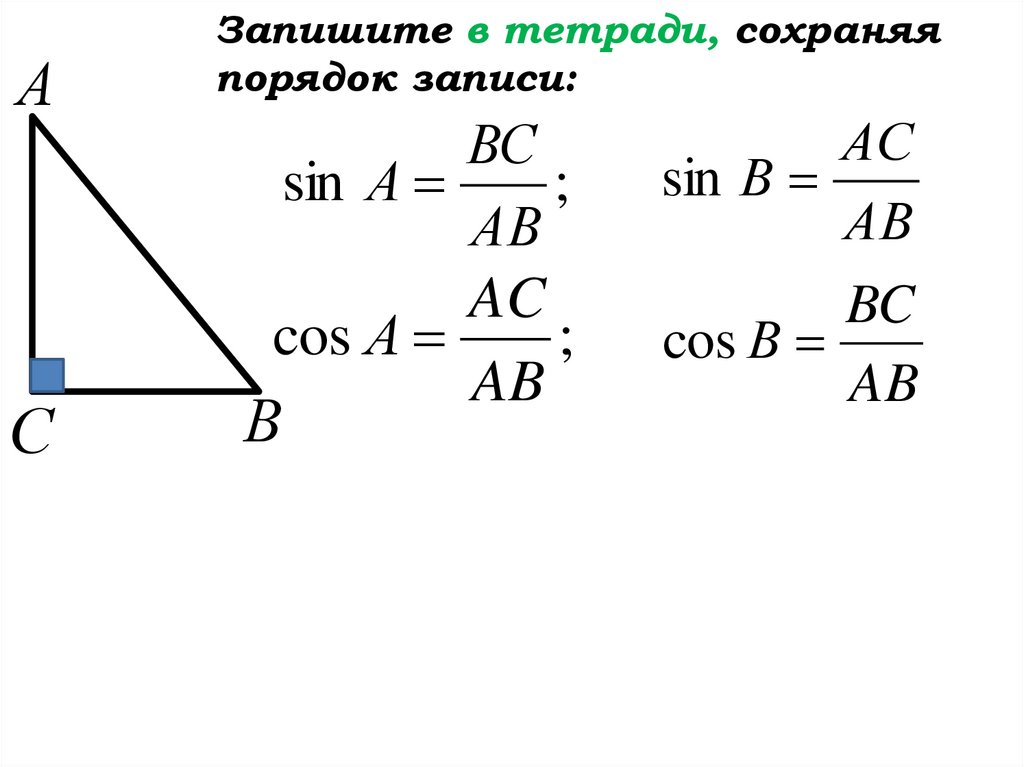
23.

А
С
Запишите в тетради, сохраняя
порядок записи:
ВС
sin А
;
АВ
AC
cos А
;
AB
В
АС
sin В
АВ
BC
cos В
AB

24.

Стр.156, п.66
Прочитайте определение
тангенса острого угла
прямоугольного треугольника.
Что нужно знать, чтобы
указать чему будет равен
тангенс острого угла
прямоугольного треугольника?
tg тангенс угла

25.

А
С
Запишите в тетради, сохраняя
порядок записи:
ВС
sin А
;
АВ
AC
cos А
;
AB
АС
sin В
АВ
BC
cos В
AB
...
tgА ;
...
...
tgB
...
В

26.

А
С
ВС
sin А
;
АВ
AC
cos А
;
AB
BC
tgА
;
В
AC
АС
sin В
АВ
BC
cos В
AB
AC
tgB
BC
Дайте определение синуса,
косинуса, тангенса
!!

27.

А
С
ВС
sin А
;
АВ
AC
cos А
;
AB
BC
tgА
;
В
AC
АС
sin В
АВ
BC
cos В
AB
AC
tgB
BC
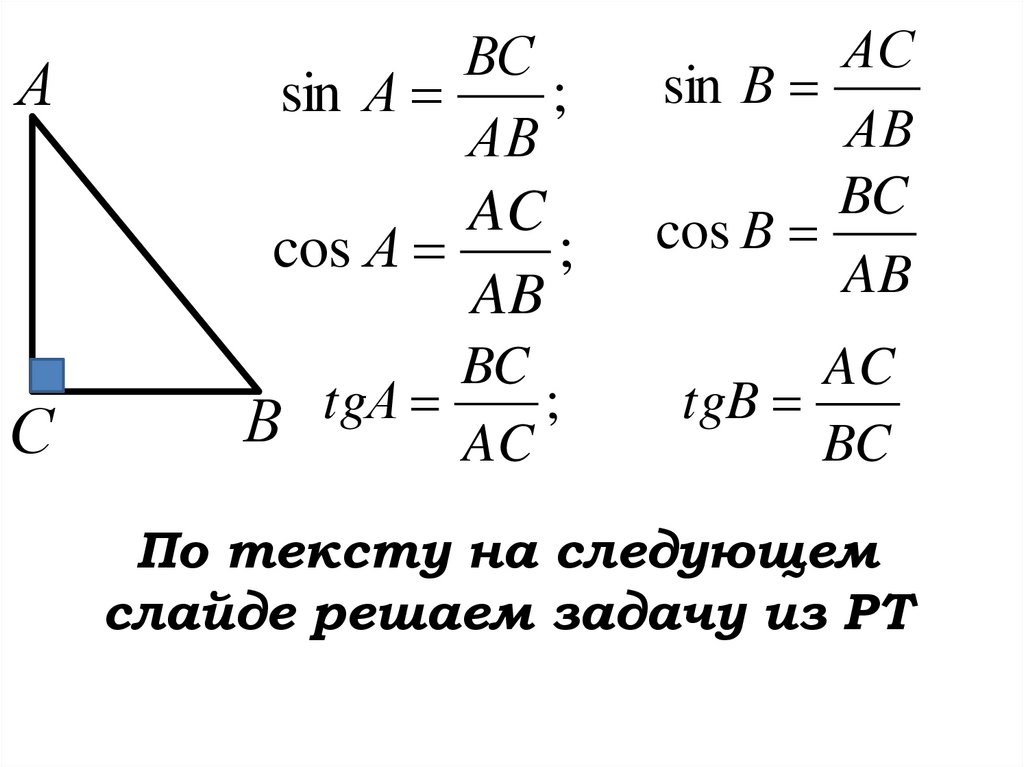
По тексту на следующем
слайде решаем задачу из РТ

28.

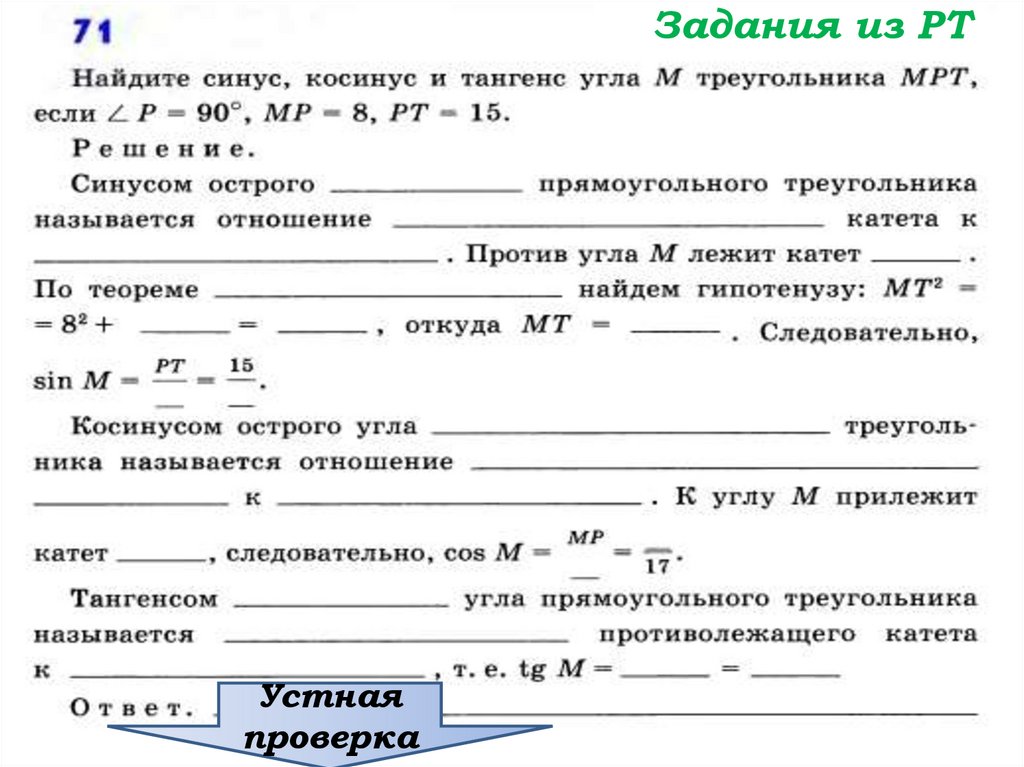
Задания из РТ
Устная
проверка

29.

Работа в парах
По чертежам на карточке
записать
синусы, косинусы и тангенсы
острых углов прямоугольных
треугольников
Устная
проверка

30.

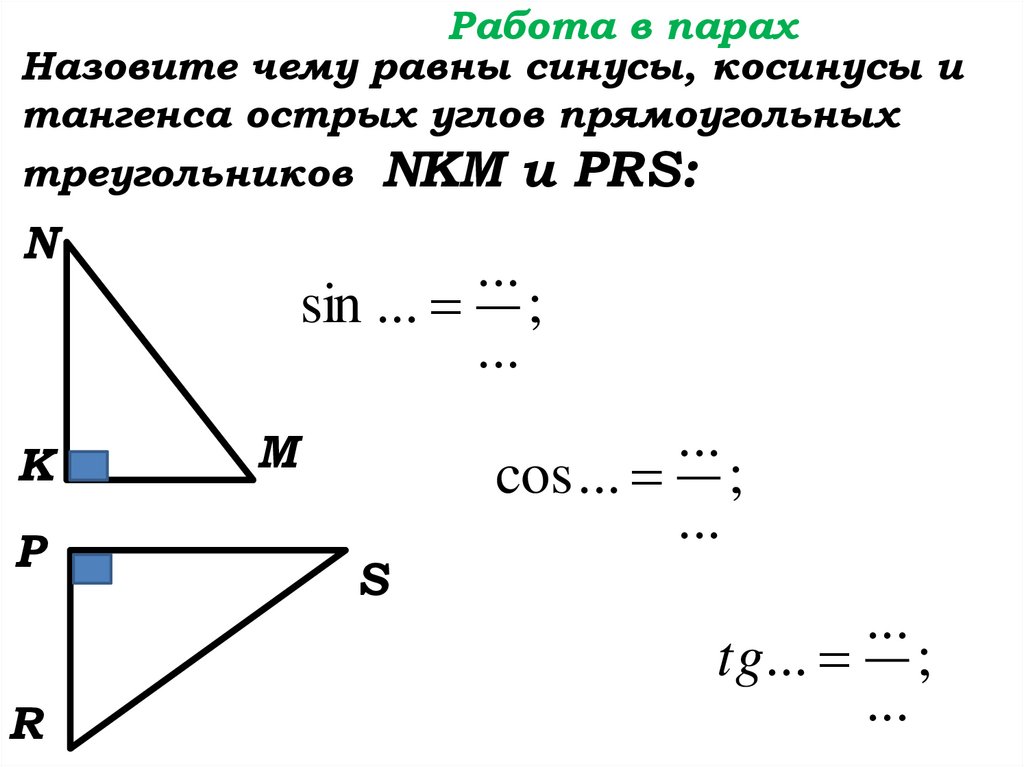
Работа в парах
Назовите чему равны синусы, косинусы и
тангенса острых углов прямоугольных
треугольников NKM и PRS:
N
К
Р
R
...
sin ... ;
...
...
cos ... ;
...
М
S
...
tg... ;
...

31.

А
С
В
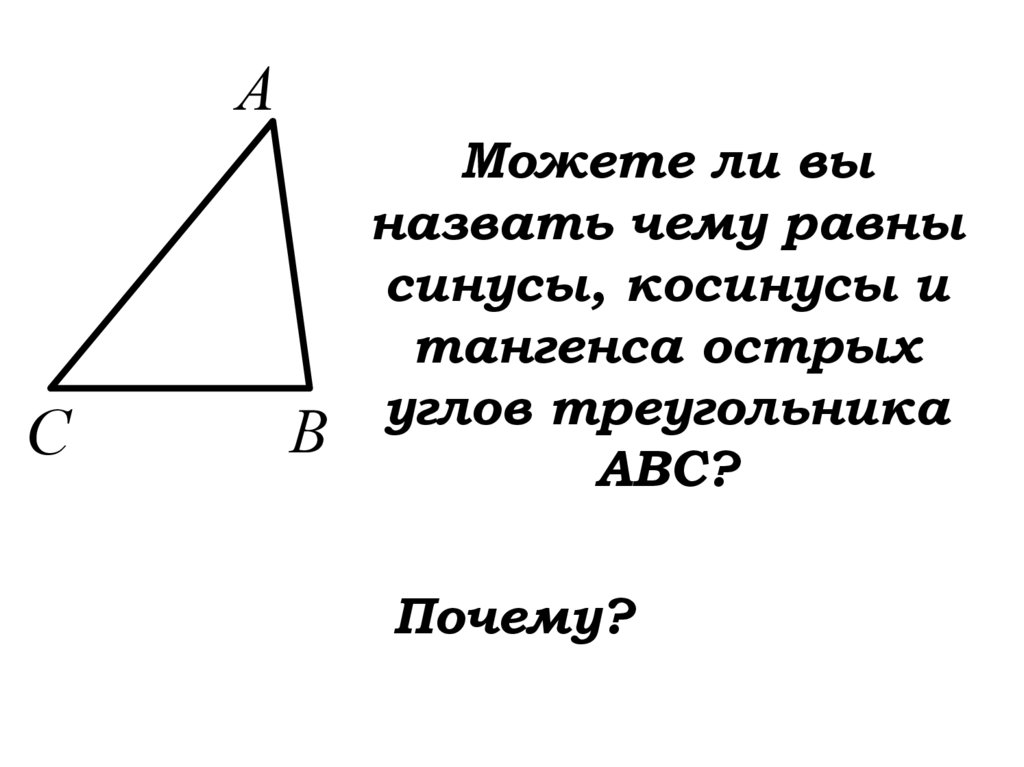
Можете ли вы
назвать чему равны
синусы, косинусы и
тангенса острых
углов треугольника
ABC?
Почему?

32.

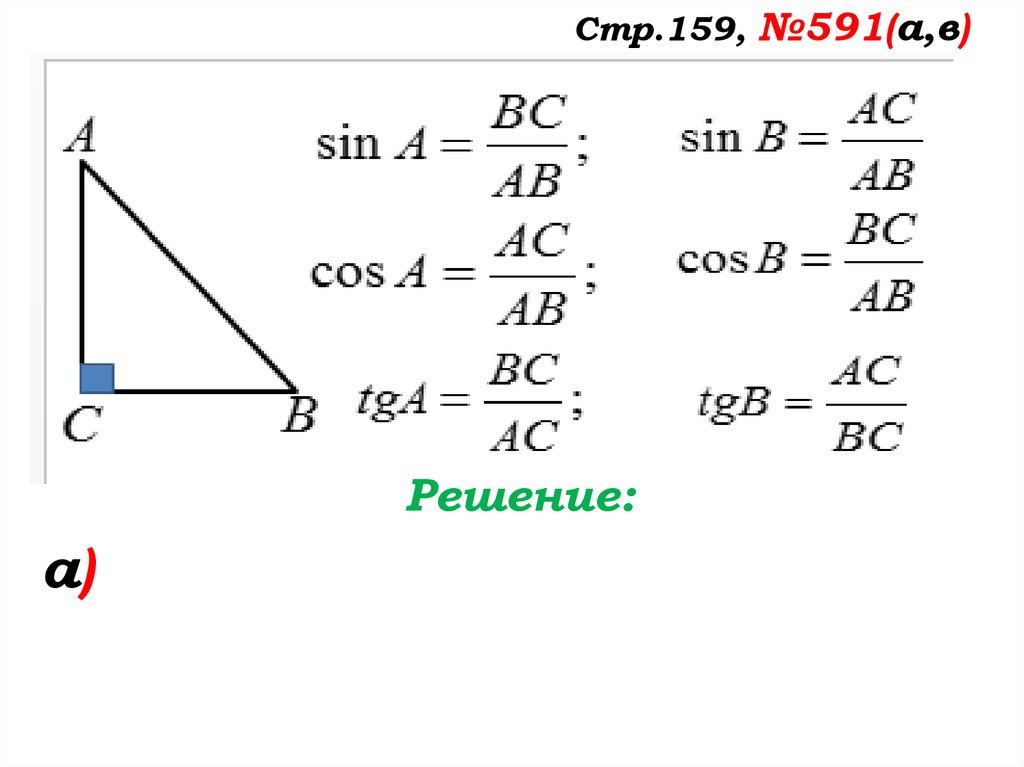
Стр.159, №591(а,в)
Прочитайте задание.
Как предлагаете его
выполнять?
Все ли известно?
Как найти неизвестные
элементы?

33.

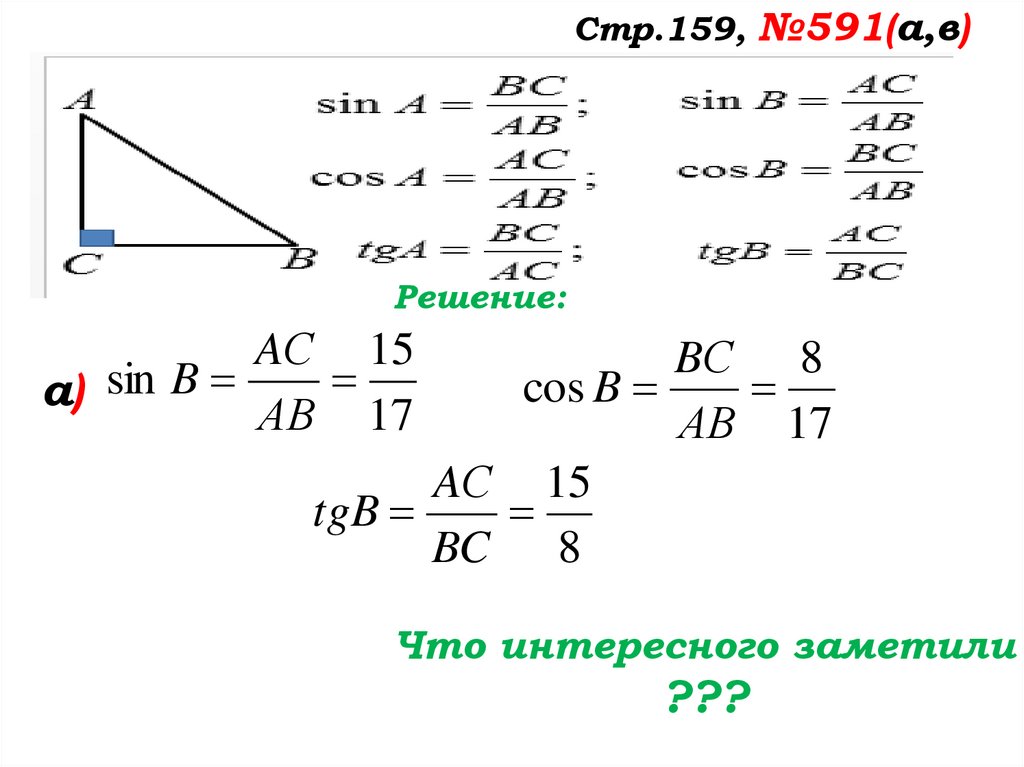
Стр.159, №591(а,в)
Решение:
а)

34.

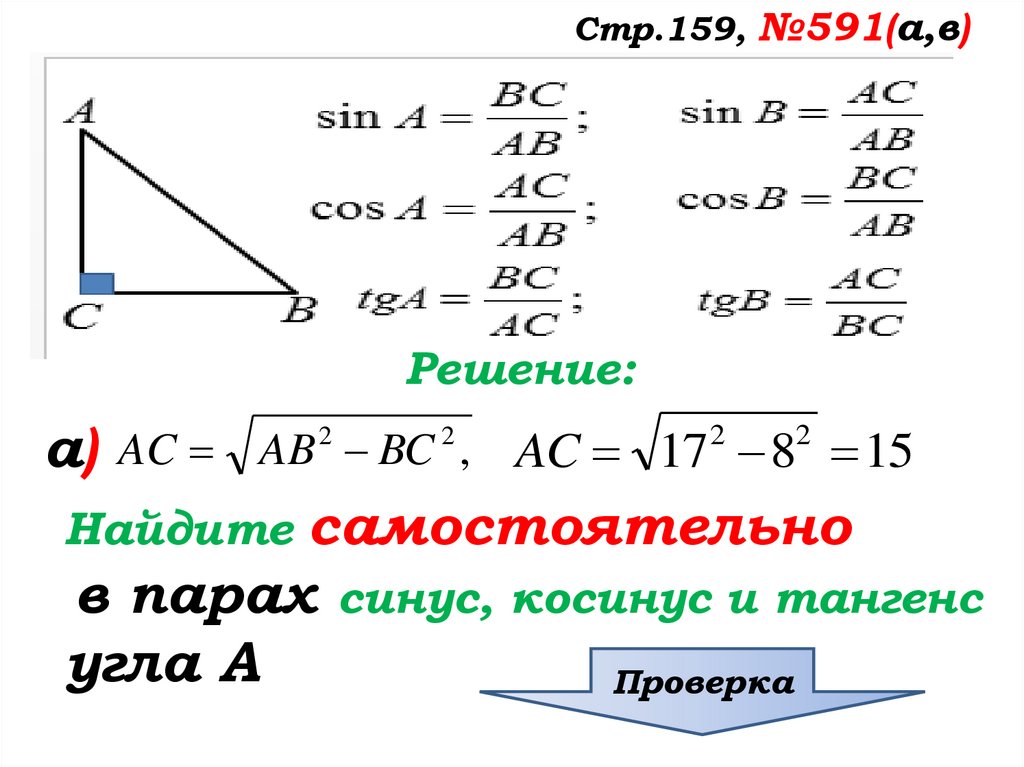
Стр.159, №591(а,в)
Решение:
а)
AC AB 2 BC 2 , AC 172 82 15
самостоятельно
в парах синус, косинус и тангенс
угла А
Проверка
Найдите

35.

Стр.159, №591(а,в)
а) AC
Решение:
AB 2 BC 2 ,
AC 17 8 15
2
2
AС 15
ВС 8
cos А
sin А
;
АВ 17
АВ 17
BС 8
tgА
АC 15 Найдите самостоятельно
в парах синус, косинус и
Проверка
тангенс угла В

36.

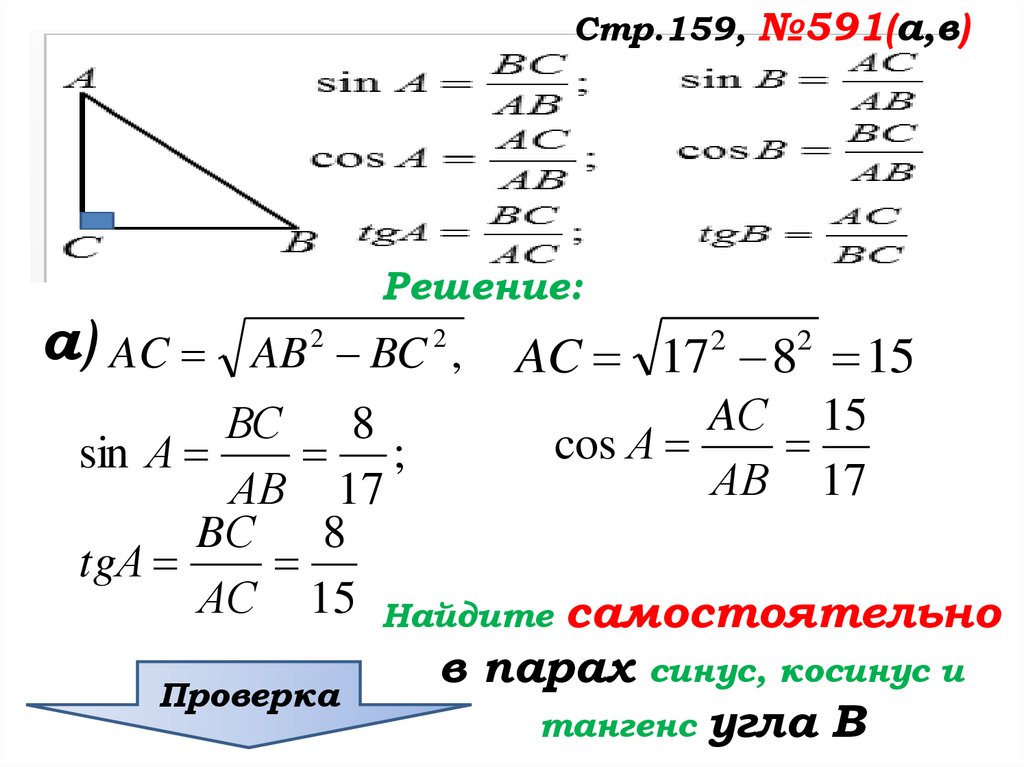
Стр.159, №591(а,в)
Решение:
AС 15
а) sin B
АВ 17
BС 8
cos B
АВ 17
AС 15
tgB
BC 8
Что интересного заметили
???

37.

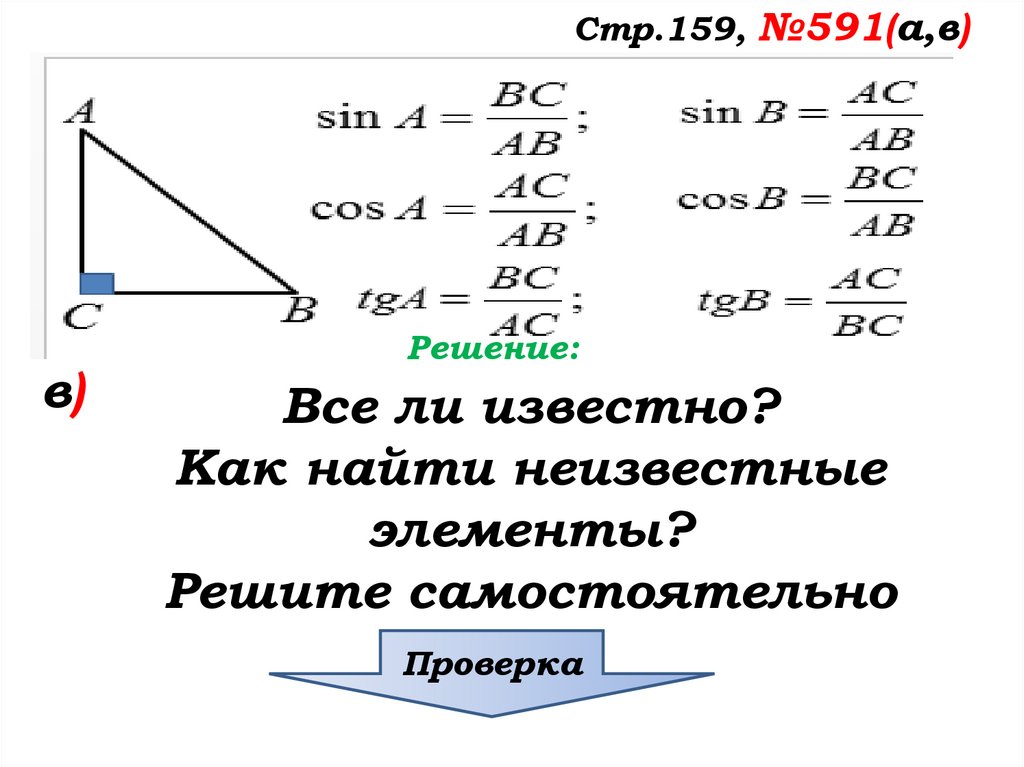
Стр.159, №591(а,в)
в)
Решение:
Все ли известно?
Как найти неизвестные
элементы?
Решите самостоятельно
Проверка

38.

Стр.159, №591(а,в)
в)
Решение:
AB
AC BC ,
2
2
AB 2 1 5
2
2
AС 2 tgA BС 1
BС 1
;
sin A
; cos A
AC 2
АВ
АВ
5
5
AС 2 cos B BС 1 ; tgB AС 2 2
sin B
;
BC 1
АВ
5
АВ
5
Подтвердились ли выводы по заданию а) ?

39.

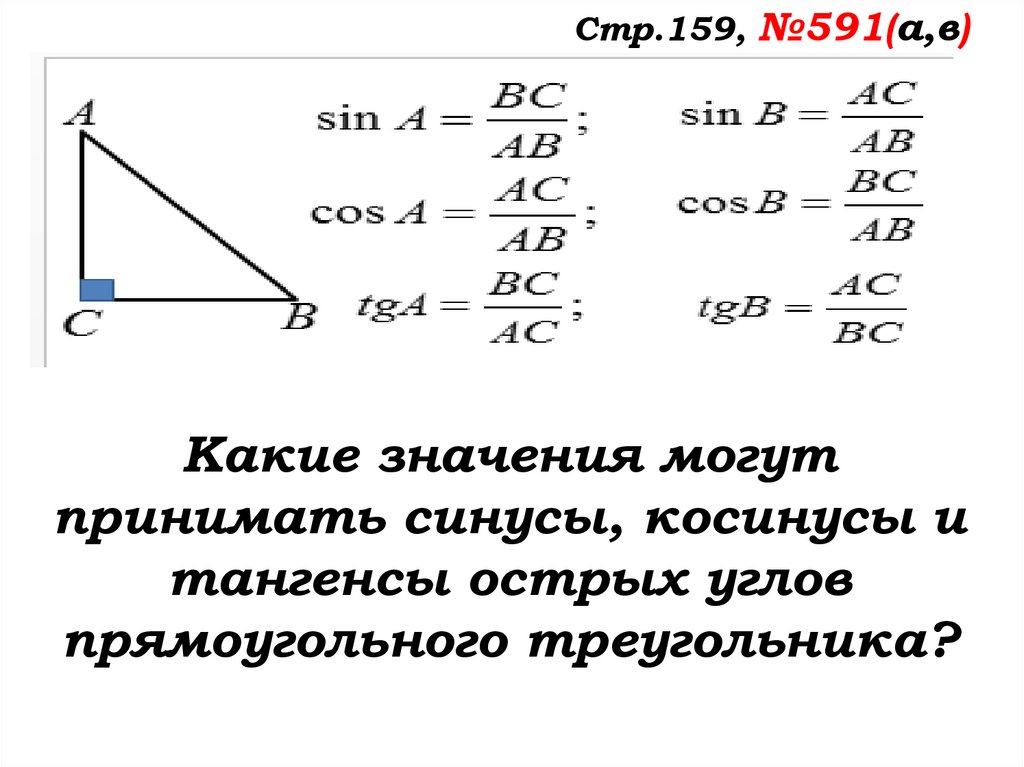
Стр.159, №591(а,в)
Какие значения могут
принимать синусы, косинусы и
тангенсы острых углов
прямоугольного треугольника?

40.

Стр.159, №591(а,в)
Вывод 1:
Синусы, косинусы и тангенсы
острых углов прямоугольного
треугольника всегда
…

41.

Стр.159, №591(а,в)
Вывод 1:
Синусы, косинусы и тангенсы
острых углов прямоугольного
треугольника всегда
положительны

42.

Используя формулы,
ВС
sin А
АВ
и
AC
cos А
AB
а) найдите самостоятельно
sin A
cos A

43.

Используя формулы,
ВС и cos А AC
sin А
AB
АВ
а) sin A BC AC BC AB BC
:
cos A AB AB AB AC AC
Что такое для угла А
BC
?
AC

44.

Используя формулы,
ВС
sin А
АВ
AC
cos
А
и
AB
sin
A
BC
AC
BC
AB
BC
а)
:
cos A AB AB AB AC AC
sin A
sin
A
tgA или tgA
cos A
cos A
Прочитайте полученное
равенство.
Чему равен тангенс угла
В?

45.

Вывод 1:
Синусы, косинусы и тангенсы
острых углов прямоугольного
треугольника всегда положительны
Вывод 2:
sin B
sin A
tgA
; tgB
cos B
cos A

46.

Используя формулы,
ВС
sin А
АВ
и
AC
cos А
AB
б) найдите, комментируя
sin А cos A
2
2

47.

Используя формулы,
ВС
sin А
АВ
б)
и
AC
cos А
AB
ВС 2 AC 2
) (
)
sin А cos A (
АВ
AB
2
2

48.

Используя формулы,
ВС
sin А
АВ
и
б)
AC
cos А
AB
ВС 2 AC 2
) (
)
sin А cos A (
АВ
AB
2
2
2
AC
ВС
2
2
AB
АВ
2

49.

Используя формулы,
ВС
sin А
АВ
и
AC
cos А
AB
б)
ВС 2 AC 2
) (
)
sin А cos A (
АВ
AB
2
2
AC
ВС
BC AC
2
2
2
AB
АВ
AB
2
2
2
2

50.

Используя формулы,
ВС
sin А
АВ
и
AC
cos А
AB
б)
ВС 2 AC 2
) (
)
sin А cos A (
АВ
AB
2
2
AC BC AC
AB
ВС
1
2
2
2
2
AB
АВ
AB
AB
2
2
имеем:
2
2
2

51.

Используя формулы,
ВС
sin А
АВ
AC
и cos А
AB
ВС
AC 2
2
2
2
б) sin А cos A (
) (
)
АВ
AB
2
2
2
2
2
AC
ВС
BC
AC
AB
1
2
2
2
2
AB
АВ
AB
AB
имеем:
sin А cos A 1
2
2

52.

б) sin 2 А cos 2 A ( ВС ) 2 AC 2
(
)
АВ
AB
2
2
2
2
2
ВС
AC
BC AC
AB
1
2
2
2
2
АВ
AB
AB
AB
sin А cos A 1
2
2
Основное тригонометрическое
тождество.
Как записать его для угла В?

53.

Вывод 1:
Синусы, косинусы и тангенсы острых
углов прямоугольного треугольника всегда
положительны
Вывод 2:
Вывод 3:
sin А cos A 1;
2
sin B
tgB
cos B
sin A
tgA
;
cos A
2
sin B cos B 1
2
2

54.

Устно
1.Найдите:
а) sin 2 C cos 2 C ...
б) sin 2 M cos 2 M ...
в) sin cos ...
2
2

55.

Используя формулы,
2.Найдите:
а) tgA, если
sin A n, cos A m
б) tgA, если
sin A 0, cos A 1
3
1
, cos A
в) tgA, если sin A
2
2

56.

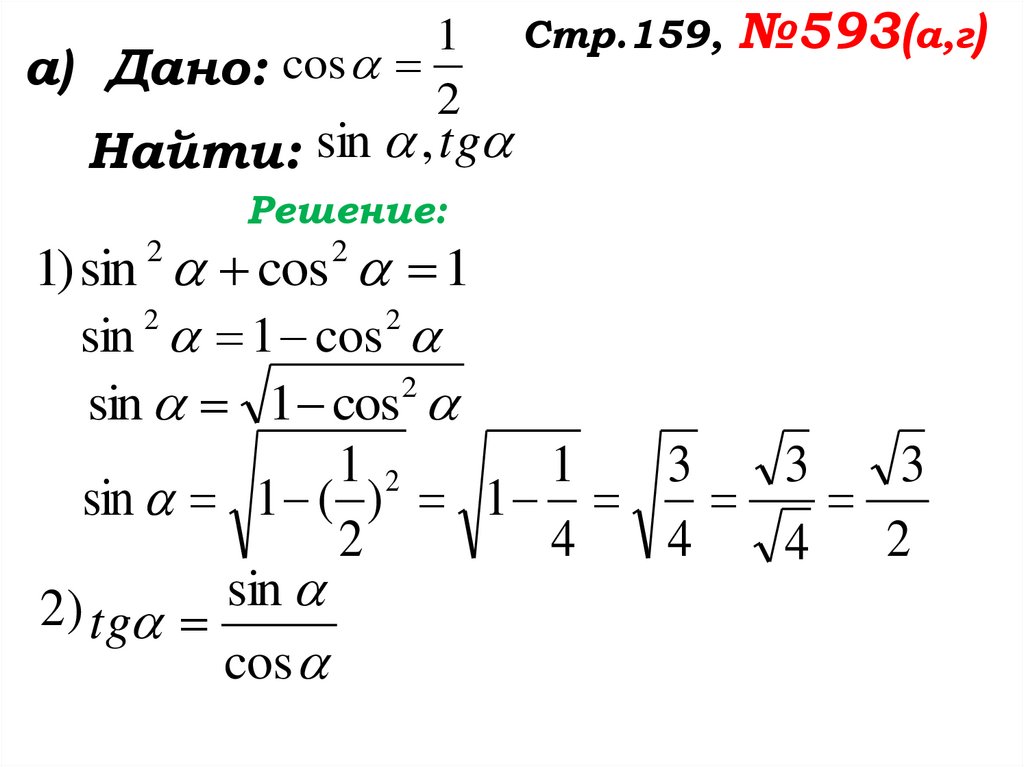
№593(а,г)
1
а) Дано: cos
2
Найти: sin , tg
Стр.159,
Решение:
Какие формулы надо
использовать, чтобы найти
требуемое?

57.

Стр.159,
1
а) Дано: cos
2
Найти: sin , tg
Решение:
1) sin cos 1
2
2
Что нужно выразить?
№593(а,г)

58.

№593(а,г)
1
а) Дано: cos
2
Найти: sin , tg
Стр.159,
Решение:
1) sin cos 1
2
2
sin 1 cos
2
2

59.

№593(а,г)
1
а) Дано: cos
2
Найти: sin , tg
Стр.159,
Решение:
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos !!!
2
2

60.

1 Стр.159, №593(а,г)
а) Дано: cos
2
Найти: sin , tg
Решение:
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
1 2
sin 1 ( )
2
2
2

61.

1 Стр.159, №593(а,г)
а) Дано: cos
2
Найти: sin , tg
Решение:
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
1 2
1
sin 1 ( ) 1
2
4
2
2

62.

1 Стр.159, №593(а,г)
а) Дано: cos
2
Найти: sin , tg
Решение:
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
1 2
1
3
sin 1 ( ) 1
2
4
4
2
2

63.

1 Стр.159, №593(а,г)
а) Дано: cos
2
Найти: sin , tg
Решение:
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
1 2
1
3
3
3
sin 1 ( ) 1
2
4
4
4 2
2
2

64.

1
а) Дано: cos
2
Стр.159,
№593(а,г)
Найти: sin , tg
Решение:
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
1 2
1
3
3
3
sin 1 ( ) 1
2
4
4
4 2
2 ) tg sin
cos
2
2

65.

1
а) Дано: cos
2
Найти:
Стр.159,
sin , tg
№593(а,г)
Решение:
2
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
2
1 2
1
3
3
3
sin 1 ( ) 1
2
4
4
4 2
sin
2 ) tg
cos
3
tg 2
1
2

66.

1
а) Дано: cos
2
Найти:
Стр.159,
sin , tg
№593(а,г)
Решение:
2
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
2
1 2
1
3
3
3
sin 1 ( ) 1
2
4
4
4 2
sin
2 ) tg
cos
3
3 1
2
tg
:
1
2 2
2

67.

1
а) Дано: cos
2
Найти:
Стр.159,
№593(а,г)
sin , tg
Решение:
2
1) sin cos 1
2
2
sin 1 cos
2
sin 1 cos
2
1 2
1
3
3
3
sin 1 ( ) 1
2
4
4
4 2
sin
2 ) tg
cos
3
3 1
3 2
2
tg
:
3
1
3
2 2
2 1
; 3
Ответ:
2
2

68.

1
г) Дано: sin 4
Найти: cos , tg
Решение:
Стр.159,
№593(г)
1) sin 2 cos 2 1
Решите самостоятельно,
обсудив ход решения
2)

69.

1
г) Дано: sin
4
Найти: cos , tg
Решение:
Стр.159,
№593(г)
1) sin cos 1
cos 2 1 sin 2
cos 1 sin 2
2
2
1 2
1
15
15
15
cos 1 ( ) 1
4
16
16
4
16
sin
2 ) tg
cos
1
1 15
1 4
1
1 15
15
4
tg
:
15 4 4
4 15
15
15 15 15
4

70.

1
г) Дано: sin
4
Найти: cos , tg
Решение:
Стр.159,
№593(г)
1) sin cos 1
cos 2 1 sin 2
cos 1 sin 2
2
2
1 2
1
15
15
15
cos 1 ( ) 1
4
16
16
4
16
sin
2 ) tg
1 cos
1 15
1 4
1
1 15
15
4
tg
:
15
15 4 4
4 15
15
15 15
4
15
Ответ:
4
; 15

71.

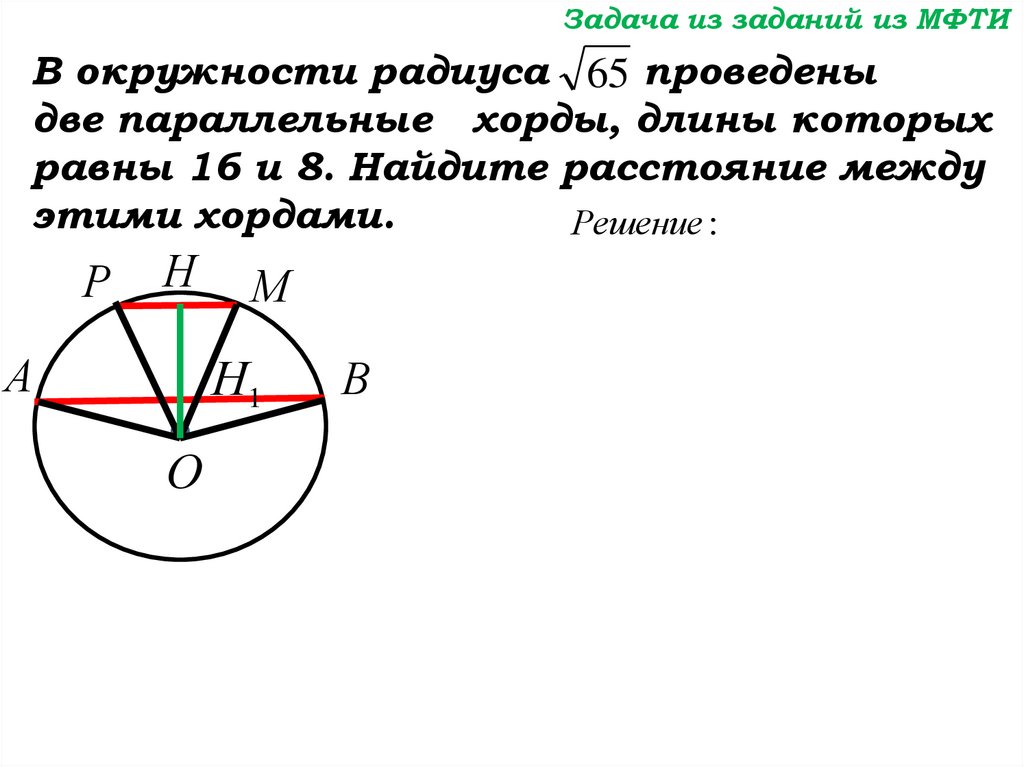
Задача из заданий из МФТИ
В окружности радиуса 65 проведены
две параллельные хорды, длины
которых равны 16 и 8. Найдите
расстояние между этими хордами.

72.

Задача из заданий из МФТИ
В окружности радиуса 65 проведены
две параллельные хорды, длины которых
равны 16 и 8. Найдите расстояние между
этими хордами.
Решение :
Р
Н
А
М
Н1
О
В

73.

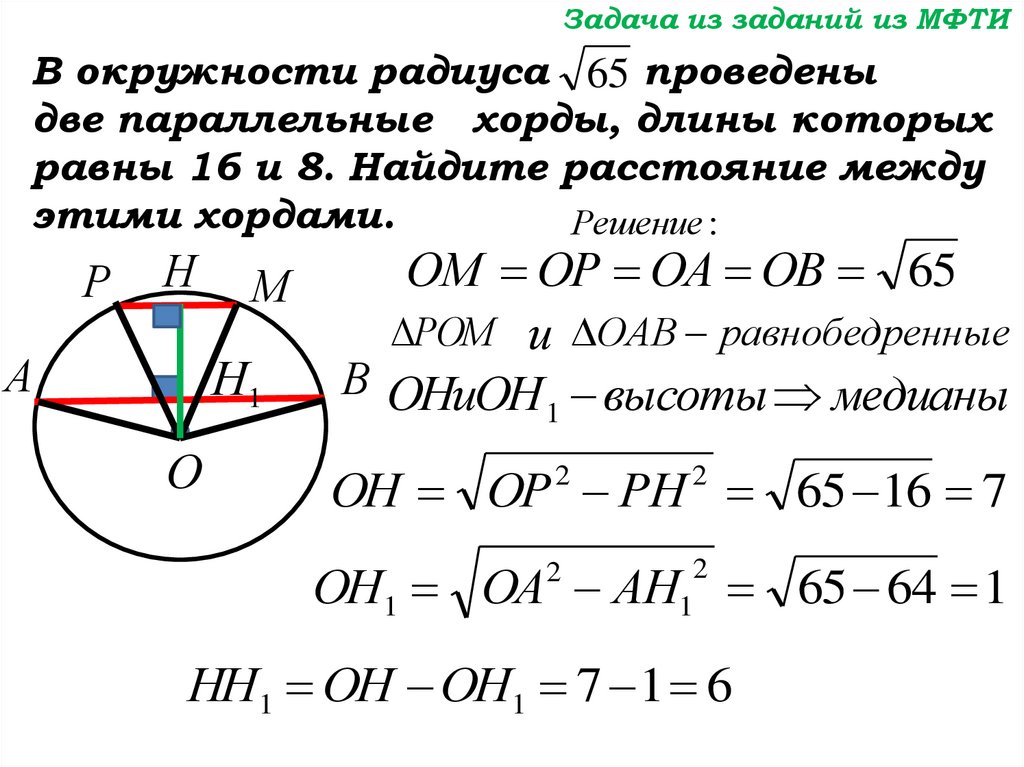
Задача из заданий из МФТИ
В окружности радиуса 65 проведены
две параллельные хорды, длины которых
равны 16 и 8. Найдите расстояние между
этими хордами.
Решение :
Р
Н
А
М
Н1
О
ОМ ОР ОА ОВ 65
РОМ и ОАВ равнобедренные
В ОНиОН высоты медианы
1
ОН ОР РН 65 16 7
2
2
ОН1 ОА АН 65 64 1
2
2
1
НН1 ОН ОН1 7 1 6

74.

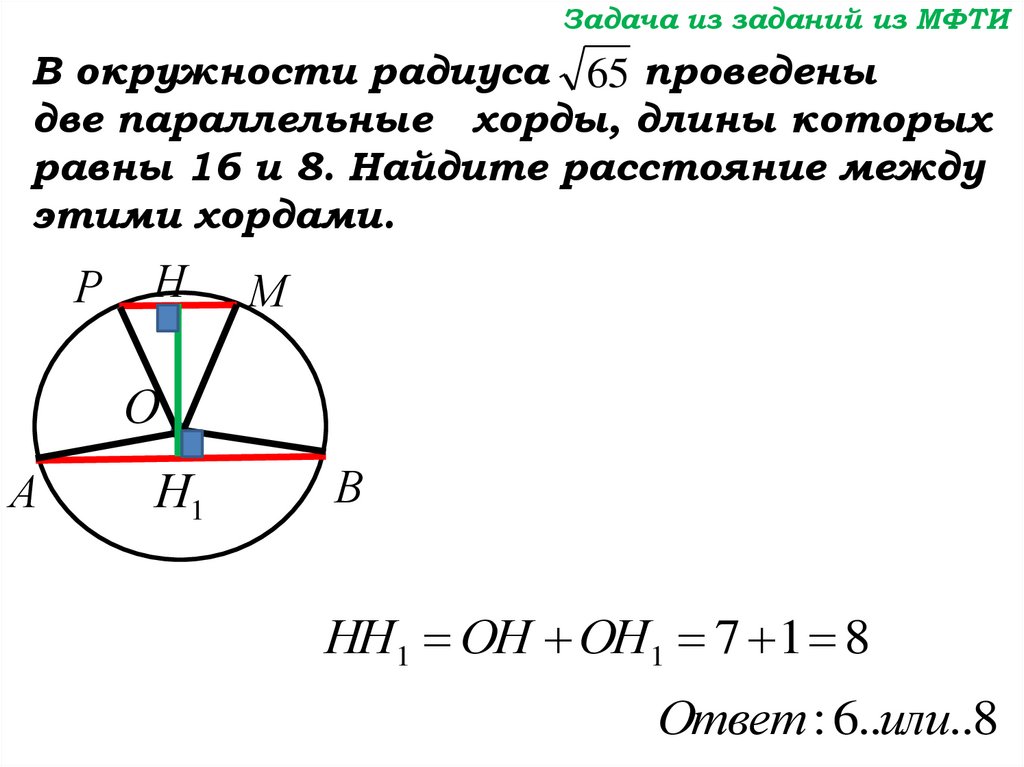
Задача из заданий из МФТИ
В окружности радиуса 65 проведены
две параллельные хорды, длины которых
равны 16 и 8. Найдите расстояние между
этими хордами.
Р
Н
М
О
А
Н1
В
НН1 ОН ОН1 7 1 8
Ответ : 6..или..8

75.

Поставьте себе оценку за урок
Критерии оценки за урок:
1. Комментировали ДЗ
2. Активно участвовали в
решении устных задач.
3. Привели решение задач,
решаемых письменно

76.

Назовите ученика, который
по вашему мнению был сегодня
на уроке лучшим