Похожие презентации:
Неопределенный интеграл. Первообразная
1.
ПЕРВООБРАЗНАЯ..
НЕОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ
Код и наименование специальности:
Наименование программы: Элементы высшей математики
Авторы лекции: Буланова Алина Николаевна, к.э.н, доцент
ГБПОУ Московский колледж бизнес-технологий
2.
По заданным производным найдите исходные функцииy 3x 2
3
y
2 x
y sin x
4
y x
y x3
y 3 x
y cos x
x5
y
5
дифференцирование
интегрирование
3.
ПЕРВООБРАЗНАЯF x первообразная
Функция F называется первообразной для функции
f, если выполняется условие
F x f x
4.
найдите производные функций:y x2
y x 2 10
y x 2 0,5
y 2 x
y x2 3
F x x c
2
f x 2 x
совокупность первообразных
5.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ• Совокупность всех первообразных F(x)+c
для функции f(x) называется неопределенным
интегралом и обозначается
f
x
dx
F
x
c
где f(x) – подинтегральная функция,
f(x)dx
–
подинтегральное
(дифференциал),
с – постоянная интегрирования.
выражение
6.
Свойства неопределенного интеграла1. f ( x)dx f ( x).
2. f x dx f ( x) C.
3. kf ( x) dx k f ( x) dx.
4. f1 x f 2 ( x) dx f1 ( x) dx f 2 ( x) dx.
1
5. f kx b dx F kx b C.
k
7.
Таблица интегралов8.
Примеры:2
• 3







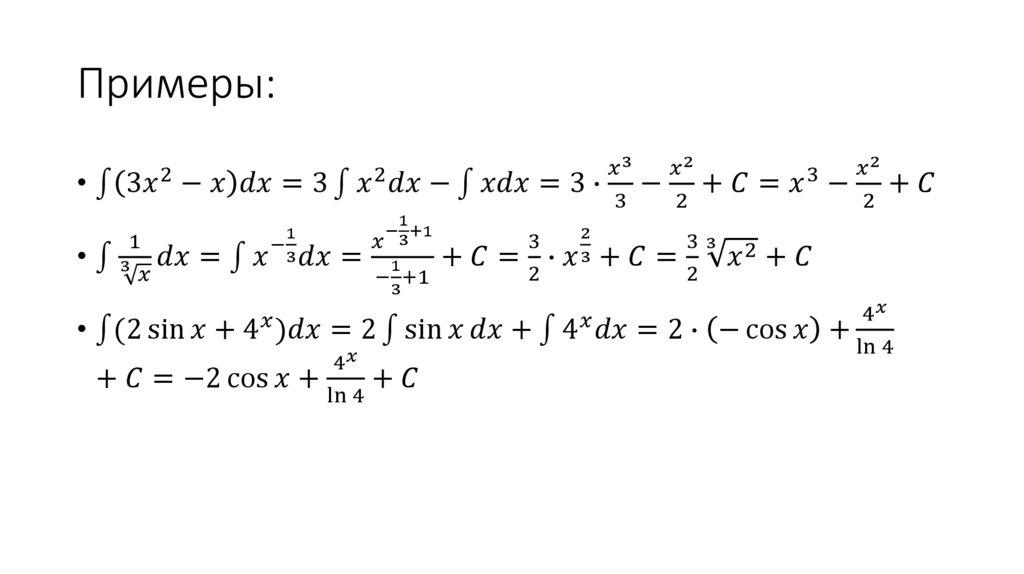


 Математика
Математика








