Дифференциальное и операторное уравнения, передаточная функция и характеристическое уравнение разомкнутой системы

1.

ТАУ
Дифференциальное и операторное уравнения, передаточная
функция и характеристическое уравнение разомкнутой
системы

2.

Математическая модель разомкнутой системы
• Чтобы произвести расчет САУ, надо иметь математическую модель системы.
• Обычно математической моделью является дифференциальное уравнение, которое
получают, анализируя физический, механический или иной процесс.
• Рассмотрим математическую модель разомкнутой системы, которая выражается
дифференциальным уравнением общего вида:
• где y – управляемая величина, x – управляющая величина; обе – функции времени;
коэффициенты ai, bi – постоянные. Правая часть описывает воздействие, левая часть
– изменение управляемой величины.
• Решение уравнения (2.1) дает полное представление об изменении управляемой
величины.

3.

Операторное уравнение
• В теории автоматического управления предпочитают иметь дело не с
дифференциальным уравнением, а с операторным уравнением, точнее
– с его особой формой, которая получила название «передаточная
функция».
• (Читается: «изображение функции x(t) есть X(p)» и т. д.)

4.

Операторное уравнение

5.

Операторное уравнение

6.

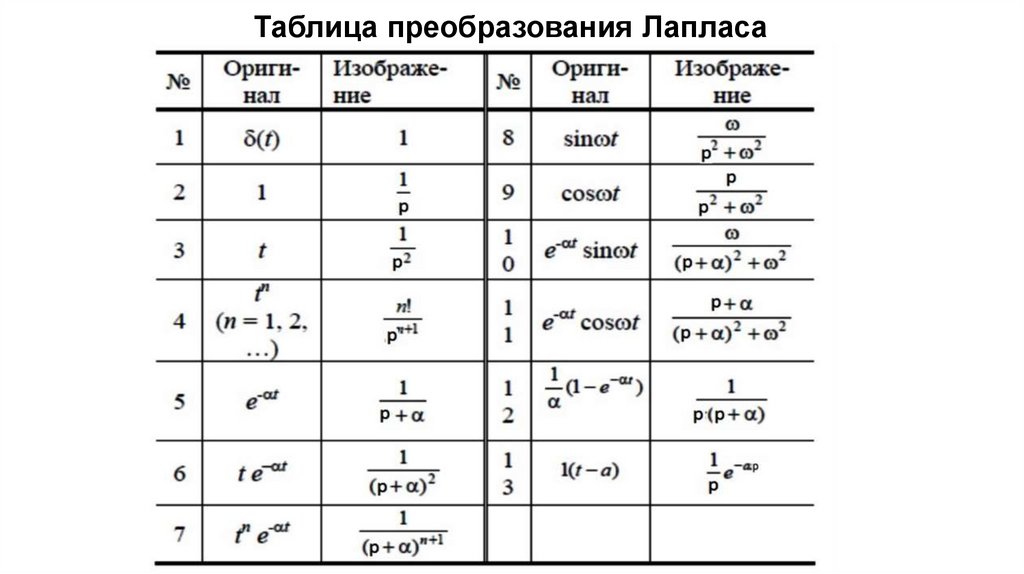
Таблица преобразования Лапласа

7.

Операторное уравнение
• Применив преобразование Лапласа к дифференциальному уравнению общего вида (2.1) ,
получаем

8.

Операторное уравнение
• Комплексный полином В(р) описывает управляющее воздействие на систему. Комплексный
полином D(p) описывает изменение управляемой величины. Введенные обозначения
позволяют представить уравнение (2.2) краткой записью:
D(p) Y(p) = B(p) X(p).
• Уравнение (2.2) и его краткую запись называют операторным уравнением.
• Особую роль в математическом описании линейных систем автоматического управления
играет отношение Y(p) / X(p). Его называют передаточной функцией и обозначают W(p).
• Выражение (2.5) является передаточной функцией разомкнутой системы, поскольку
получено из дифференциального уравнения (2.1) , записанного для разомкнутой системы.
• Операторное уравнение можно записывать, используя передаточную функцию:
Y(p) = W(p) X(p)
• Как было сказано, комплексный полином D(p) описывает изменение управляемой
величины. То есть, характеризует процесс, который происходит в системе под влиянием
управляющего воздействия. Поэтому полином D(p) называют характеристическим.
(2.6)

9.

Характеристическое уравнение
• Приравнивая его к нулю, получают характеристическое уравнение системы:
• Характеристическое уравнение позволяет найти корни и получить решение
дифференциального уравнения.
• Характеристический полином, характеристическое уравнение служат основой
исследования системы на устойчивость.
• Для преобразования Лапласа необходимо, чтобы начальные условия были
нулевыми, а дифференциальные уравнения – линейными.
• Однако, линейность уравнений, описывающих реальные технические системы,
скорее исключение, чем правило.
• В случае слабо нелинейной зависимости (типа слабо искривленной линии,
участок которой можно заменить прямой с пренебрежимой погрешностью),
осуществляют линеаризацию и ведут расчеты на отрезке прямой.

10.

Пример 1.
• Записать передаточную функцию и характеристическое уравнение для
системы, поведение которой описывается дифференциальным уравнением

11.

Пример 1
• Значит, искомая передаточная функция есть