Похожие презентации:
Тригонометрия. Угол
1.
ТРИГОНОМЕТРИЯТригономе́трия
(от греч. τρίγονο (треугольник) и греч. μετρειν
(измерять), то есть измерение треугольников) —
раздел математики, в котором изучаются
тригонометрические функции.
Данный термин впервые появился в 1595 г. как
название книги немецкого математика
Бартоломеуса Питискуса (Bartholomäus Pitiscus,
1561—1613), а сама наука ещё в глубокой
древности использовалась для расчётов в
астрономии, геодезии и архитектуре.
2.
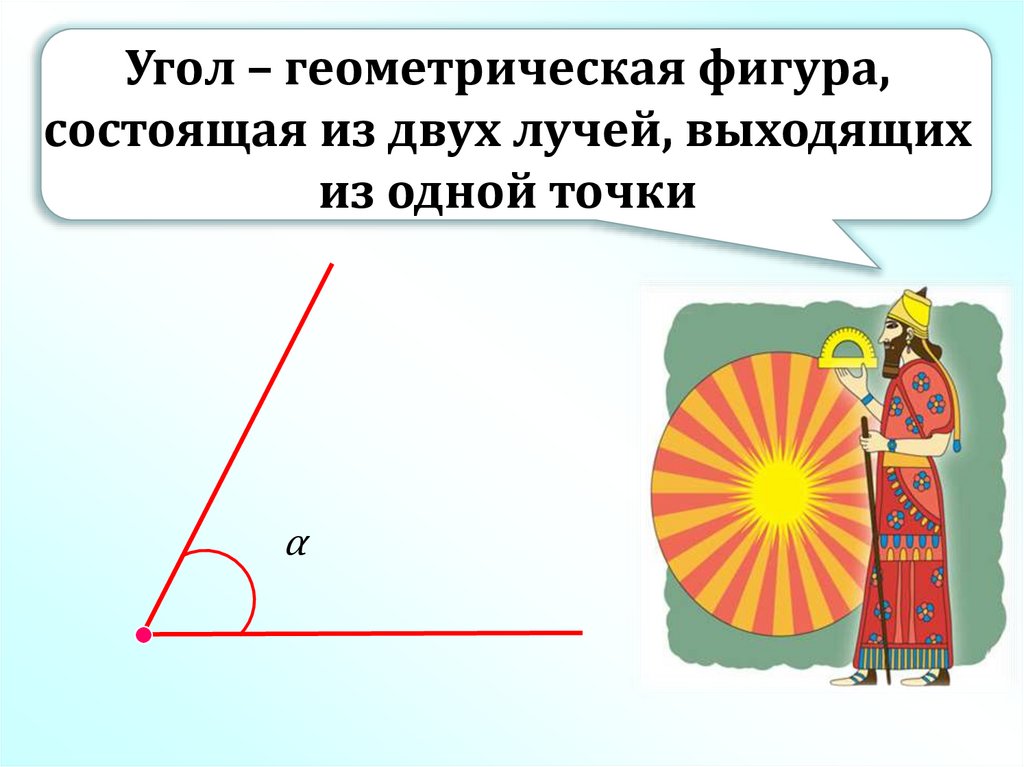
Угол – геометрическая фигура,состоящая из двух лучей, выходящих
из одной точки
α
3.
Измерение углов60
0
4.
Единицы измерения угла:1
1 минута ( 1’) - часть градуса
60
1
1 секунда ( 1’’) - часть минуты
60
A 25
0
35 24 16
0
I
II
5.
Вавилоняне считали, что за каждые суткисолнце делало один «шаг», поэтому
разделили окружность на 360 равных частей,
каждую из которых называют градусом (от
лат. gradus — шаг, ступень).
6.
Знаете ли вы, почему в окружности 360 градусов, а не 180 или,скажем, не 300?
Откуда пошла традиция делить окружность на равные части и
почему было выбрано именно такое их число?
Оказывается, этому делению мы обязаны вавилонянам.
Согласно их календарю,
продолжительность года
составляла 360 дней —
именно столько раз, по
наблюдениям древних
астрономов, солнечный диск
укладывался на годичном пути
светила.
7.
Развитие тригонометриивызвало необходимость в 19
веке введения новой меры
измерения угловрадианной.
8.
9.
Измерение углов1 радиан (от латинского radius - спица колеса) центральный угол, длина дуги которого равна
радиусу окружности
10.
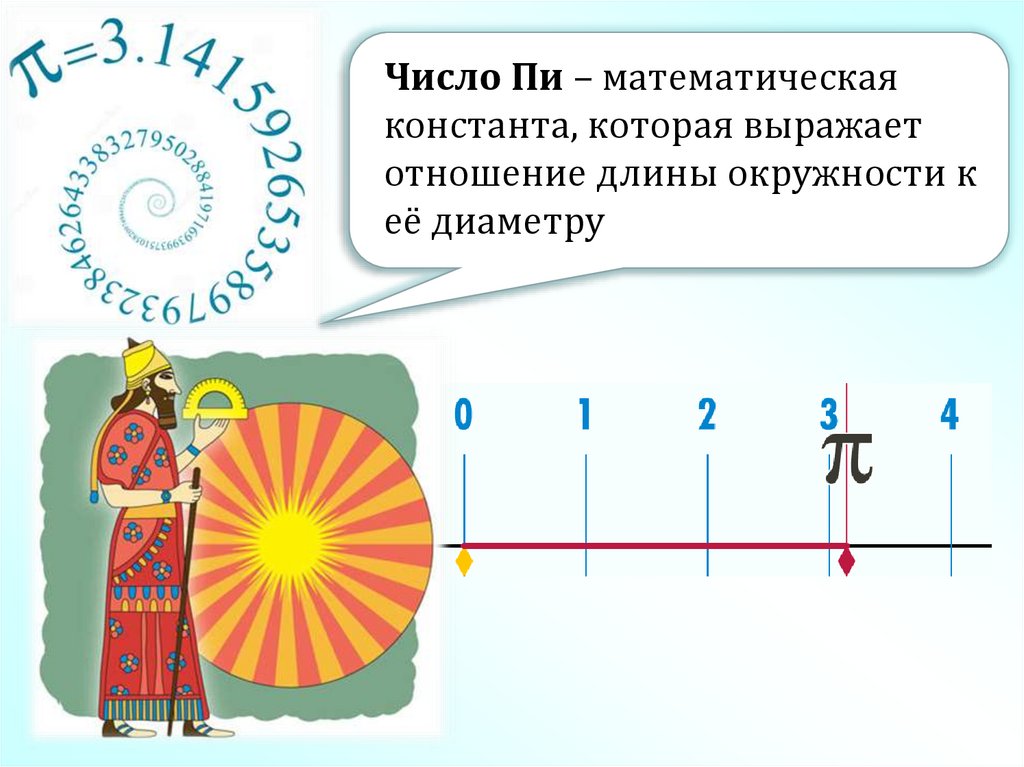
Число Пи – математическаяконстанта, которая выражает
отношение длины окружности к
её диаметру
11.
12.
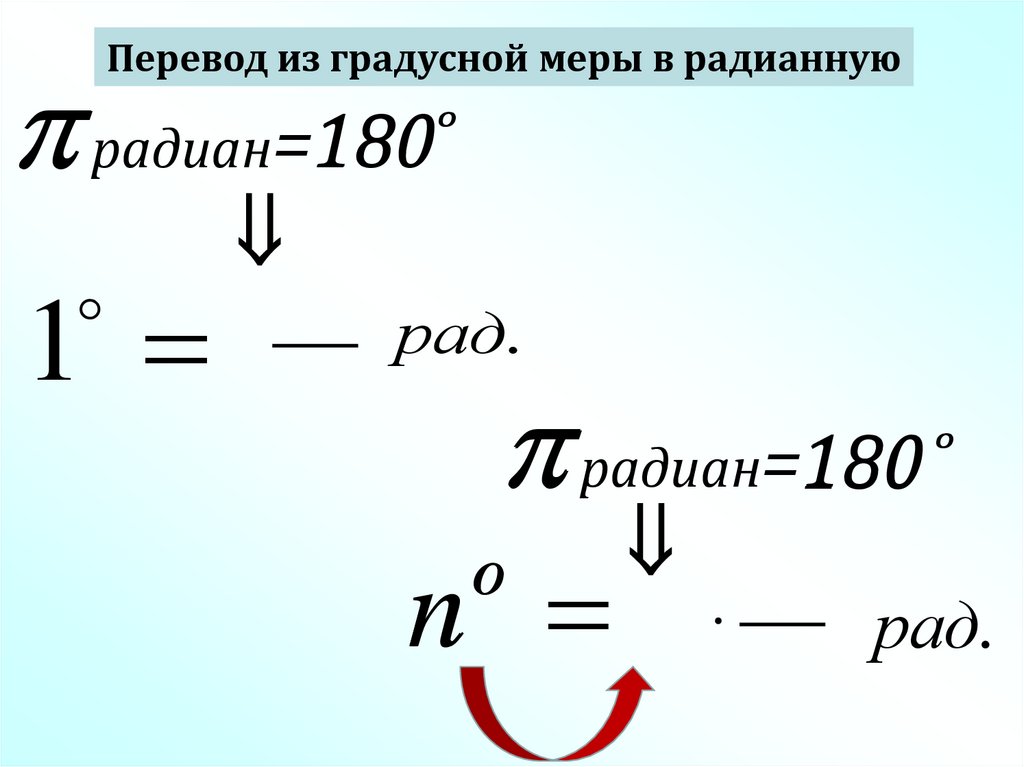
Перевод из градусной меры в радианную180 ̊
радиан=180
1
рад.
радиан=180
180 ̊
n
о
рад.
13.
Примеры:радиан=180
180
30
72
120
180 6
2
72
180 5
2
120
3
180
30
14.
Примеры:1. 60
60
рад.
рад.
3
180
90
рад
.
рад
.
2. 90
180
2
3
135
рад
.
3. 135
рад
.
4
180
15.
Переведите в радианную меру углы:45
4
180
4
240
3
10
3
270
2
5
150
6
360
2
11
330
6
18
36
5
16.
Перевод из радианной меры в градусную,если радианная мера задана с числом π.
радиан=180
a m
180
1 57
0
17.
Примеры:180
рад.
18
1.
10
10
180
рад.
2.
20
9
9
4 180
4
240
рад.
3.
3
3
18.
Переведите в градусную меру углы:рад
.
1
180
рад
.
36
5
5
37,рад
5 .
24
4
.
рад
45
10
600
рад.
3
3
рад.
135
4
19.
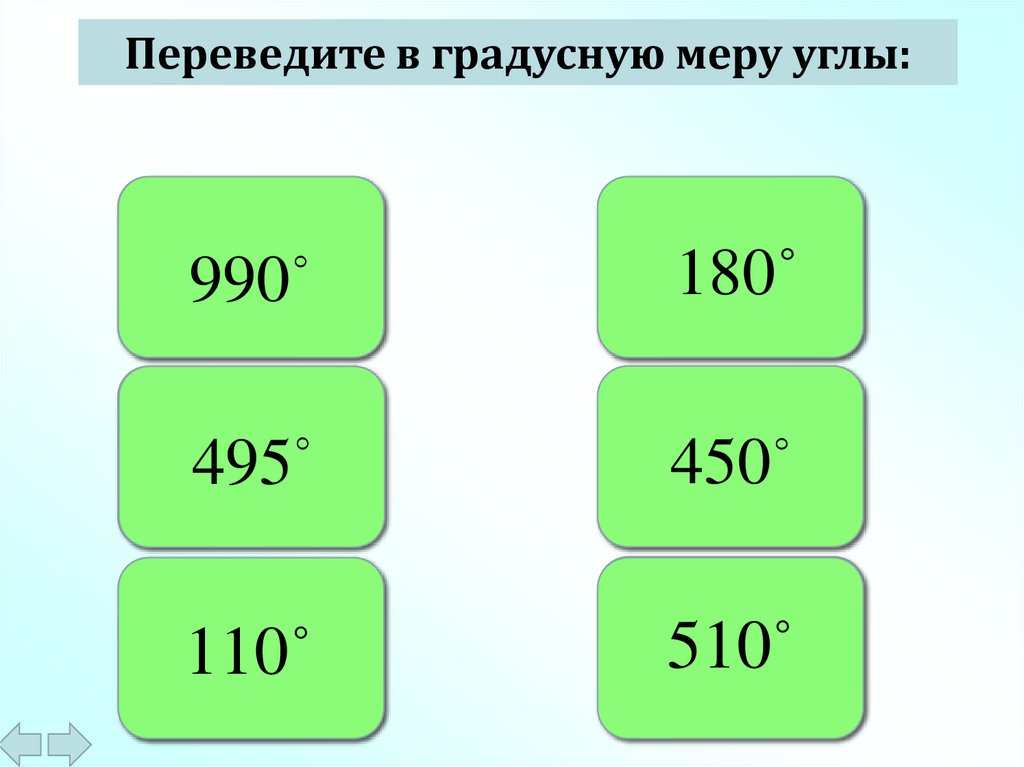
Переведите в градусную меру углы:11
рад.
990
2
11
рад.
495
4
11
110рад.
18
180
рад .
5
рад.
450
2
17
510рад.
6
20.
Перевод из радианной меры в градуснуюn n
180
рад.
1. 2 2
m рад. m
Примеры:
180
180
0
2
114,6
3,14
1 57
0
0
2 2 57 114
0
180
21.
Переведите в градусную меру углы:0
2
рад
.
114
5 рад
.
285
.
1,57
рад
90
1 ,269
рад.
рад.
314
18000
9
,42
рад.
540
22.
Перевод из градусной меры в радианную:n n
180
рад
.
Перевод из радианной меры в градусную:
m рад. m 180
m рад. m 57
m рад. m
180
23.
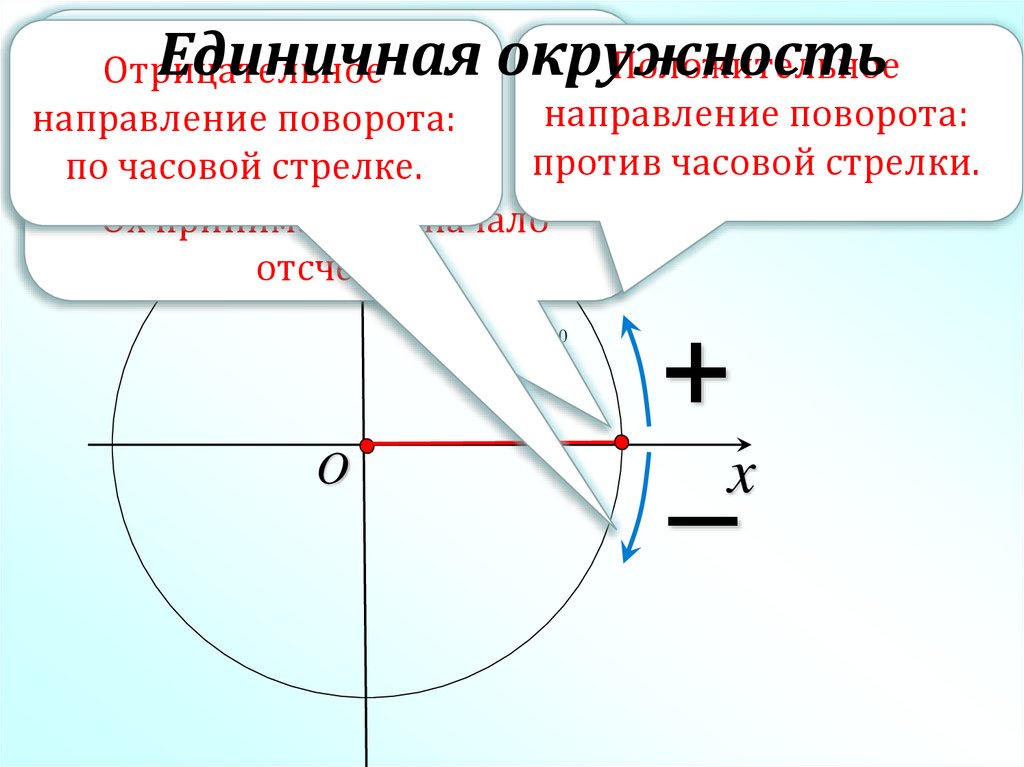
Единичная окружностьОкружность с центром в начале системы координат Oxy и
Положительное
Отрицательное
Точку
пересечения
радиусом,
равным
единице, называется единичной, а
направление поворота:
направление
поворота:
окружности
с – тригонометрическим.
ограниченный
ей круг
против часовой стрелки.
по
часовой стрелке.
y частью оси
положительной
Ох 0принимают за начало
3200
497
отсчета
540
O
+
x
–
24.
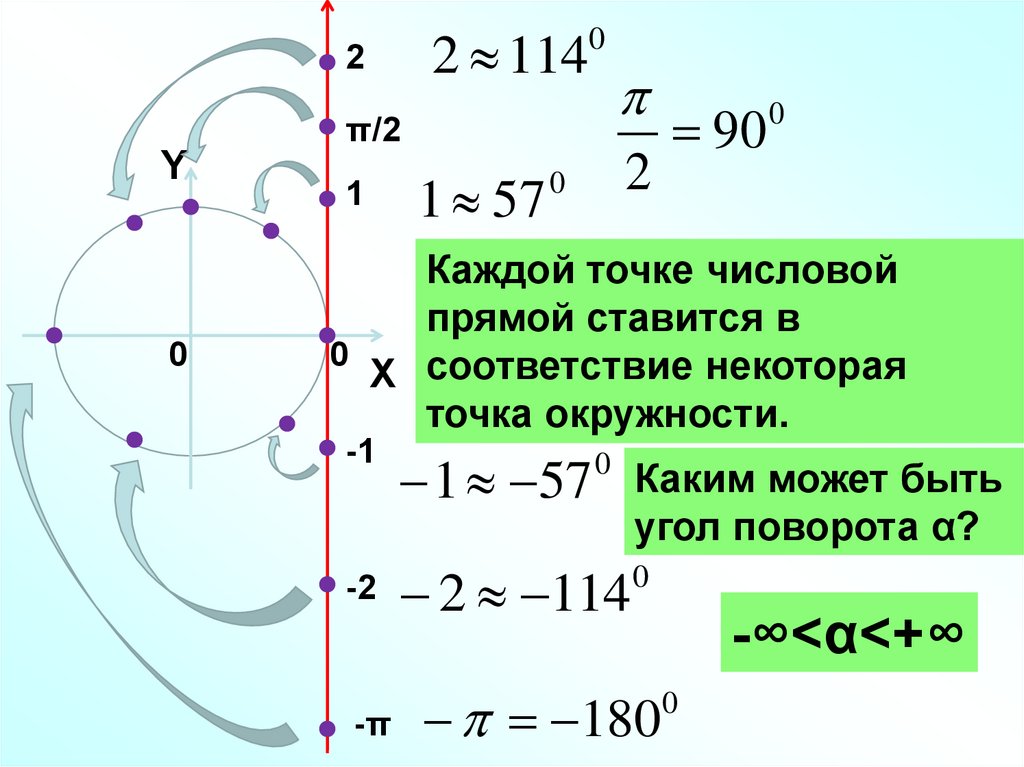
2 1142
0
0
90
2
π/2
Y
0
1
1 57
0
Каждой точке числовой
прямой ставится в
0
X соответствие некоторая
точка окружности.
-1
1 57
0
Каким может быть
угол поворота α?
-2 2 114 0
-π
180
-∞<α<+∞
0
25.
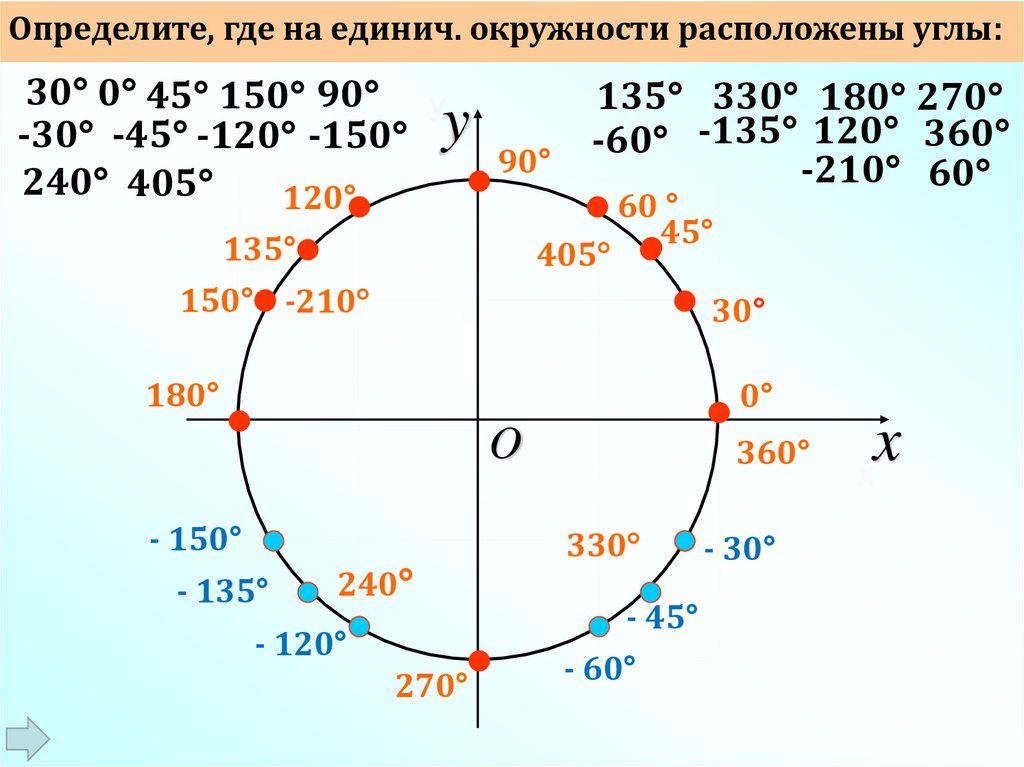
Определите, где на единич. окружности расположены углы:30 0 45 150 90 у
-30 -45 -120 -150 y
90°
240 405
120°
135°
150° -210
135 330 180 270
-60 -135 120 360
-210 60
405
60 °
45°
30°
180°
0°
O
- 150°
- 135°
240
- 120°
270°
360°
330
- 45°
- 60°
- 30°
x
Х
26.
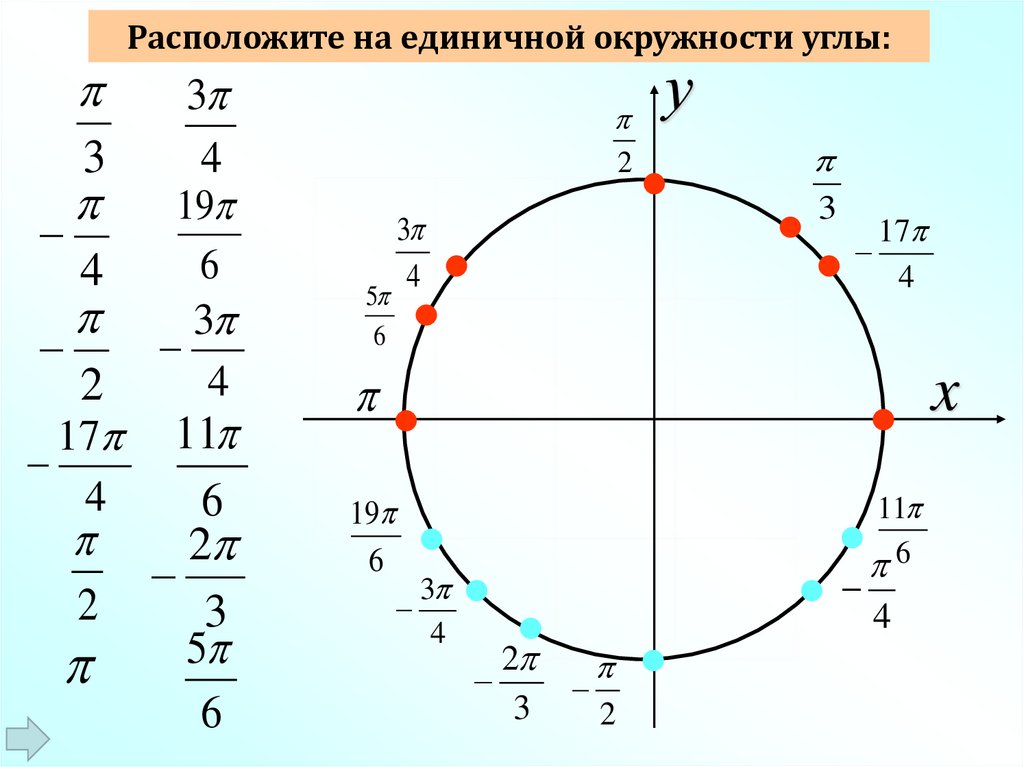
34
2
17
Расположите на единичной окружности углы:
3
4
19
6
3
4
11
4
6
2
2
3
5
6
2
5
6
у
3
3
4
17
4
x
19
6
3
4
2
3
2
11
6
4
27.
Единичная окружностьЗаписать с помощью двойных неравенств в градусах и
радианах координатные четверти
y
II четверть
I четверть
90 ° < < 180 °
2
0° < < 90°
Y
0
90⁰ π/2
π
180⁰
180° < < 270°
3
2
II
I
O0
III
IV
2π
X
«Главные точки окружности»
2
x
1 360⁰
270° < < 360°
3
2
2
270⁰ 3π/2
III четверть
IVчетверть
«Главные углы поворота»
28.
Определите, в какой четверти расположены углы:y
8
3
II четверть
O
220 0
III четверть
III четверть
5
9
I четверть
25 0
x
= 25°
5
=
9
= 220°
8
=
3
29.
30.
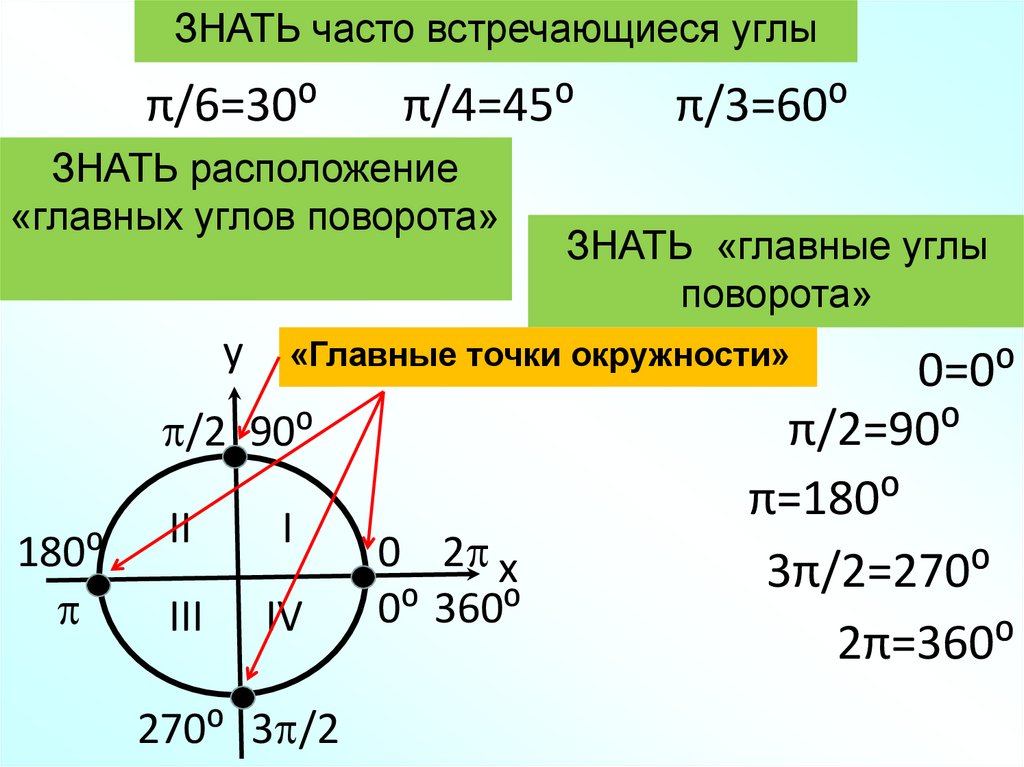
ЗНАТЬ часто встречающиеся углыπ/6=30⁰
π/4=45⁰
ЗНАТЬ расположение
«главных углов поворота»
y
ЗНАТЬ «главные углы
поворота»
«Главные точки окружности»
/2 90⁰
180⁰
π/3=60⁰
II
I
III
IV
270⁰ 3 /2
0 2 x
0⁰ 360⁰
0=0⁰
π/2=90⁰
π=180⁰
3π/2=270⁰
2π=360⁰










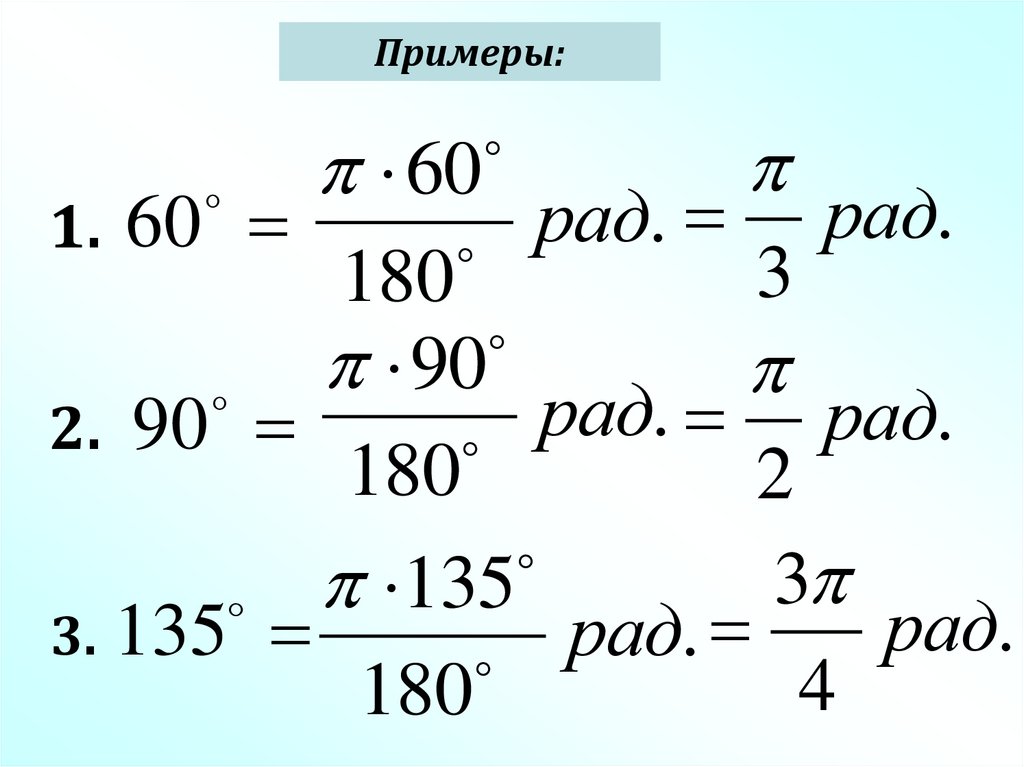










 Математика
Математика