Тригонометрия. Радианная мера угла

1.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОУ ВПО ЛНР «ЛУГАНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ ТАРАСА
ШЕВЧЕНКО»
ОП «КОЛЛЕДЖ ЛУГАНСКОГО НАЦИОНАЛЬНОГО
УНИВЕРСИТЕТА
ИМЕНИ ТАРАСА ШЕВЧЕНКО»
Презентация по математики на тему:
«Тригонометрия»
Выполнила студентка
2 курса, специальности
«делопроизводство»,
дневного отделения
Карабутова Анна

2.

• Тригономеетрия (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю», то есть
измерение треугольников) — раздел математики, в котором изучаются
тригонометрические функции и их использование в геометрии. Данный термин
впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса
Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для
расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и
форму Земли)

3.

Радианная мера угла
Центральный угол, опирающийся на дугу, длина которой равна
радиусу окружности, называется углом в 1 радиан.
радусная мера угла в 1 радиан равна:
Так как дуга длиной πR (полуокружность), стягивает центральный
угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.

4.

1 рад= (180/π)°≈57°18'
1°=π/180°≈0,017 рад
180°=π рад≈3,14 рад
Если угол содержит α радиан, то его градусная мера равна
• α рад=(180/π·α)°
• α°=π/180∙α рад
Обычно при обозначении меры угла в радианах наименование
«рад» опускают.

5.

Задание 1
1. sin π/3 = sin 180°/3 = sin 60°;
2. cos 7π/6 = cos 7 · 180°/6 = cos 210°;
3. tg π = tg 180°;
4. sin π/4 = sin 180°/4 = sin 45°;
5. tg 2π/3 = tg 2 · 180°/3 = tg 120°;
6. ctg π/2 = ctg 180°/2 = ctg 90°;
7. sin 3π/2 = sin 3 · 180°/2 = sin 270°;
8. cos 5π/4 = cos 5 · 180°/4= cos 225°.

6.

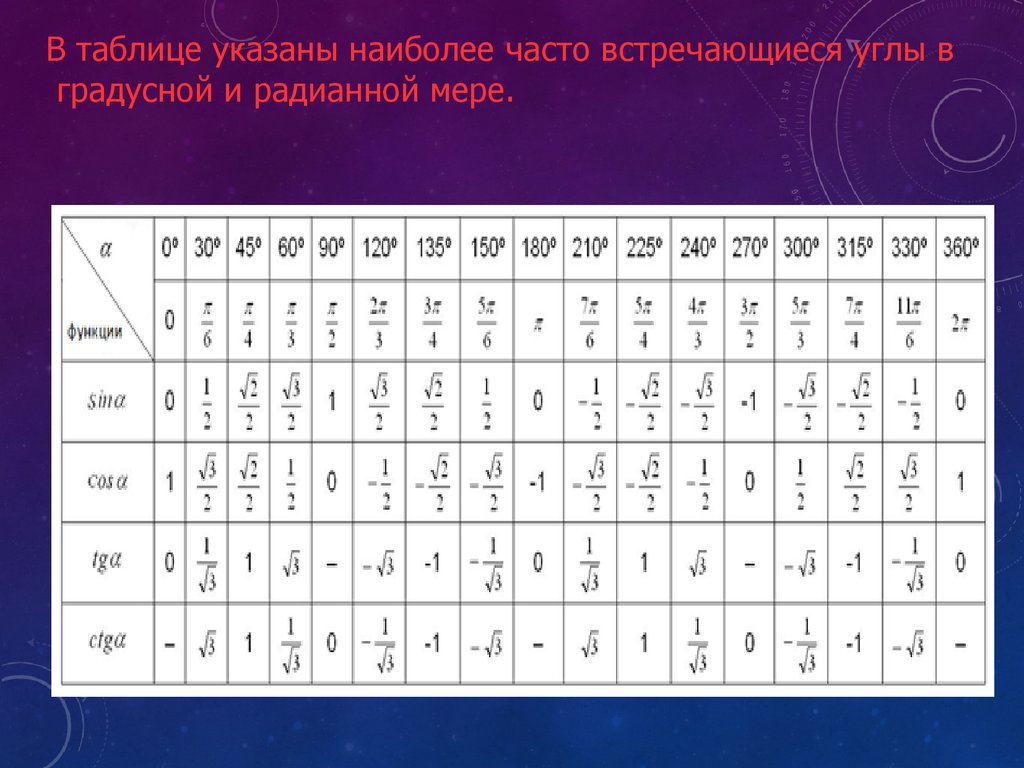
В таблице указаны наиболее часто встречающиеся углы в
градусной и радианной мере.

7.

Тригонометрические функции
Синус и косинус могут быть описаны следующим образом:
если соединить любую точку (x, y) на единичной окружности с
началом координат (0, 0), получается отрезок, находящийся под
углом относительно положительной полуоси абсцисс. Тогда
действительно:
сos α = х
sin α = y
При подстановке этих значений в уравнение окружности
сos²α+ sin²α =1

8.

Используется следующая общепринятая нотация:
сos²x= (cos x)²
Тут же наглядно описывается периодичность
тригонометрических
функций, так как соответствующее углу положение
отрезка
не зависит от количества «полных оборотов»:
sin(x+2πκ)=sin(x)
cos(x+2πκ)=cos(x)
для всех целых чисел κ, то есть
• κϵΖ

9.

• Тригонометрические формулы
1. Соотношение между тригонометрическими функциями одного и того
же аргумента

10.

2. Формулы сложения (вычитания) аргументов

11.

4. Формулы двойного аргумента

12.

Формулы преобразования суммы и разности
тригонометрических функций в произведение
3.

13.

4.
Четность нечетность тригонометрической
функции

14.

ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ПО
ЧЕТВЕРТЯМ

15.

• Задание 1
Определите, в какой координатной четверти находится аргумент
тригонометрической функции:
1. sin 8π/9;
2. tg 12π/15;
3. cos 9π/10;
4. cos 7π/18;
5. sin 3π/5;
6. ctg 5π/3;
7. tg 4π/9;
8. cos 9π/20.
Для начала переведем все углы из радиан в градусы по правилу: π →
180°. А затем найдем координатную четверть, ориентируясь по
границам: 90°, 180°, 270°, 360°. Имеем:

16.

1. sin 8π/9 = sin (8 · 180/9) = sin 160°; т.к. 160° ∈ [90°; 180°], это II
четверть;
2. tg 12π/15 = tg (12 · 180/15) = tg 144°; т.к. 144° ∈ [90°; 180°], это II
четверть;
3. cos 9π/10 = cos (9 · 180/10) = cos 162°; т.к. 162° ∈ [90°; 180°], это II
четверть;
4. cos 7π/18 = cos (7 · 180/18) = cos 70°; т.к. 70° ∈ [0°; 90°], это I
четверть;
5. sin 3π/5 = sin (3 · 180/5) = sin 108°; т.к. 108° ∈ [90°; 180°], это II
четверть;
6. ctg 5π/3 = ctg (5 · 180/3) = ctg 300°; т.к. 300° ∈ [270°; 360°], это IV
четверть;
7. tg 4π/9 = tg (4 · 180/9) = tg 80°; т.к. 80° ∈ [0°; 90°], это I четверть;
8.cos 9π/20 = cos (9 · 180/20) = cos 81°; т.к. 81° ∈ [0°; 90°], это I
четверть.

17.

18.

19.

СПАСИБО ЗА ВНИМАНИЕ!!!