Определения sinα, cosα, tgα, ctgα на окружности

1.

Урок № 82
Определения sinα, cosα, tgα, ctgα
на окружности.
Некоторые важные значения для
sinα, cosα, tgα, ctgα.
Понятие синуса
встречается уже в III в. до н. э. и
имел название джива (тетева лука) ,
в IX в. заменено на арабское слово
джайб (выпуклость) ,
XII в. заменено на латинское
синус (изгиб, кривизна) .
Косинус – это дополнительный синус.
Тангенс переводится с латинского
как «касающийся».

2.

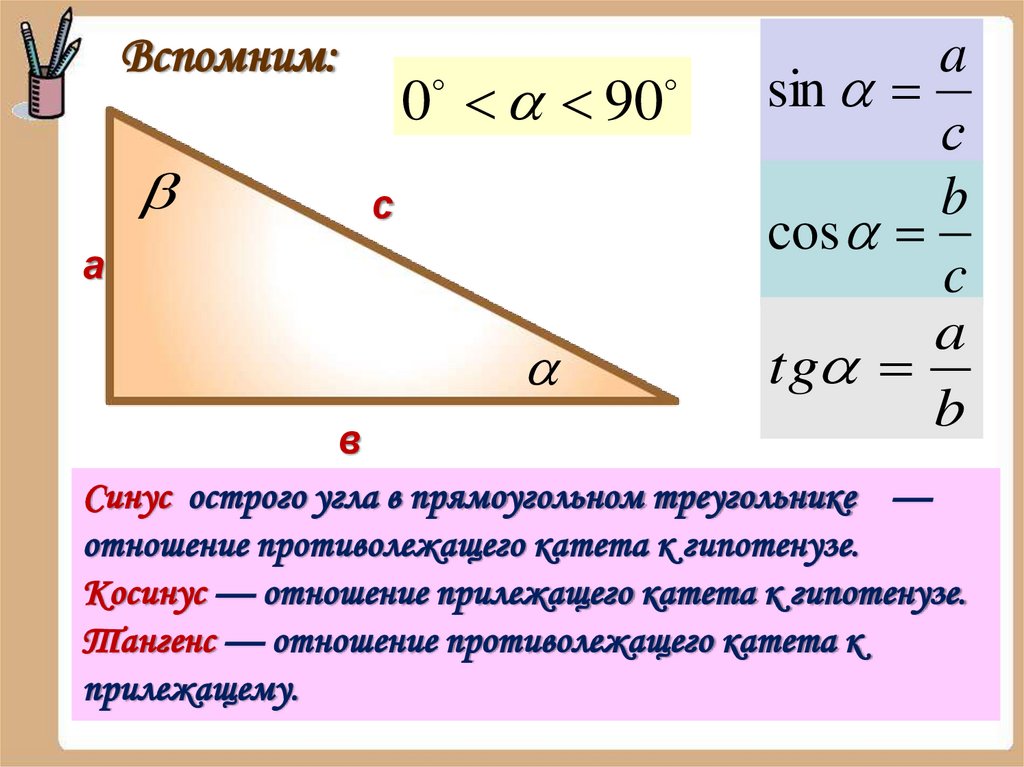
Вспомним:
0 90
с
а
a
sin
с
b
cos
c
a
tg
b
в
Синус острого угла в прямоугольном треугольнике —
отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к
прилежащему.

3.

В XVIII веке Леонард Эйлер
дал современные, более
общие определения,
расширив область
определения этих функций
на всю числовую ось.
угол поворота
R

4.

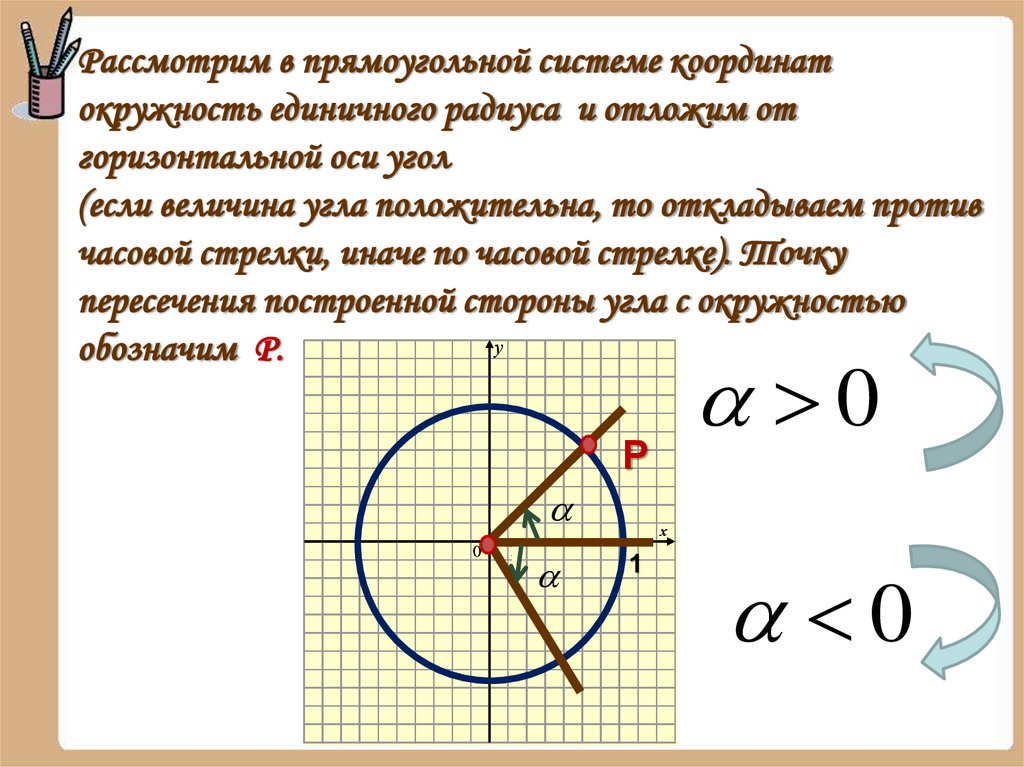
Рассмотрим в прямоугольной системе координат
окружность единичного радиуса и отложим от
горизонтальной оси угол
(если величина угла положительна, то откладываем против
часовой стрелки, иначе по часовой стрелке). Точку
пересечения построенной стороны угла с окружностью
у
обозначим Р.
0
Р
1
0
1
х
1
0

5.

Синус угла определяется как ордината точки
P sin y
cos x
Косинус — абсцисса точки P
Тангенс – отношение ординаты к абсциссе
точки P
y
sin
tg
tg
x
cos
Котангенс – отношение абсциссы к ординате
точки P
x
cos
ctg
ctg
y
sin

6.

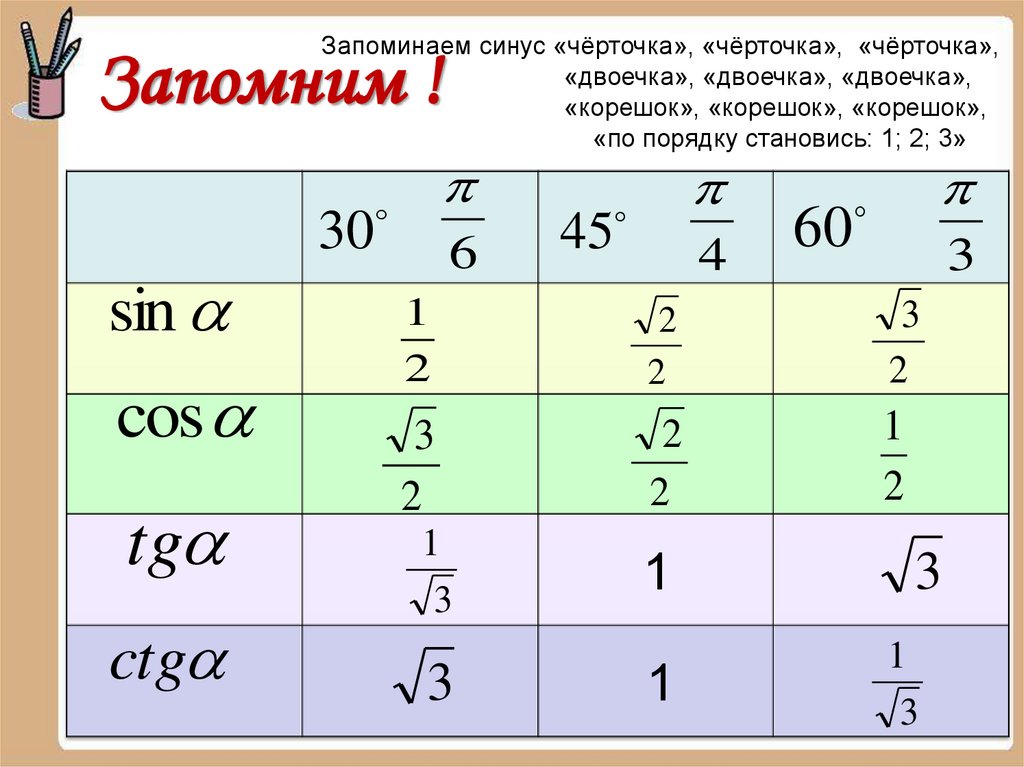
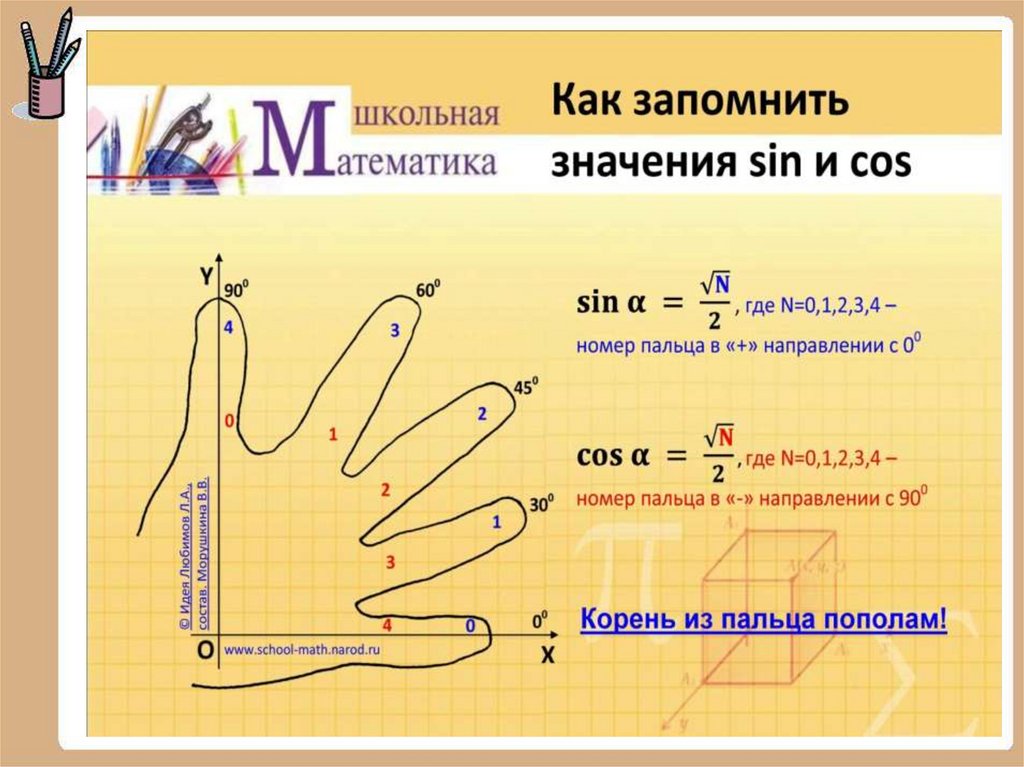
Запоминаем синус «чёрточка», «чёрточка», «чёрточка»,
«двоечка», «двоечка», «двоечка»,
«корешок», «корешок», «корешок»,
«по порядку становись: 1; 2; 3»
Запомним !
30
sin
cos
tg
ctg
6
45
4
60
3
1
2
2
2
3
2
3
2
2
2
1
2
1
3
1
3
1
1
3
3

7.

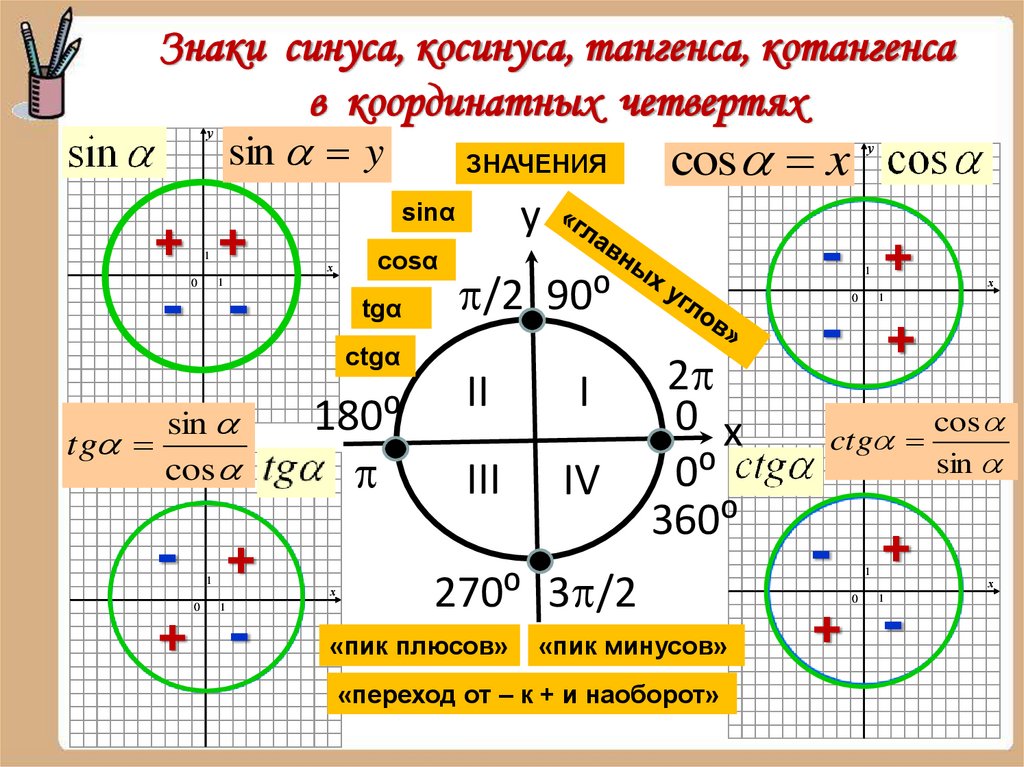
Знаки синуса, косинуса, тангенса, котангенса
в координатных четвертях
sin y
ЗНАЧЕНИЯ
cos x
sinα
y
у
у
+ +
1
х
cosα
1
0
- -
tgα
/2 90⁰
ctgα
sin
tg
у
cos
- +
+ 1
0
1
180⁰
х
II
I
III
IV
1
2
0 x
0⁰
360⁰
«пик минусов»
«переход от – к + и наоборот»
х
1
0
270⁰ 3 /2
«пик плюсов»
- +
- +
cos
ctgу
sin
- +
+ 1
0
1
х

8.

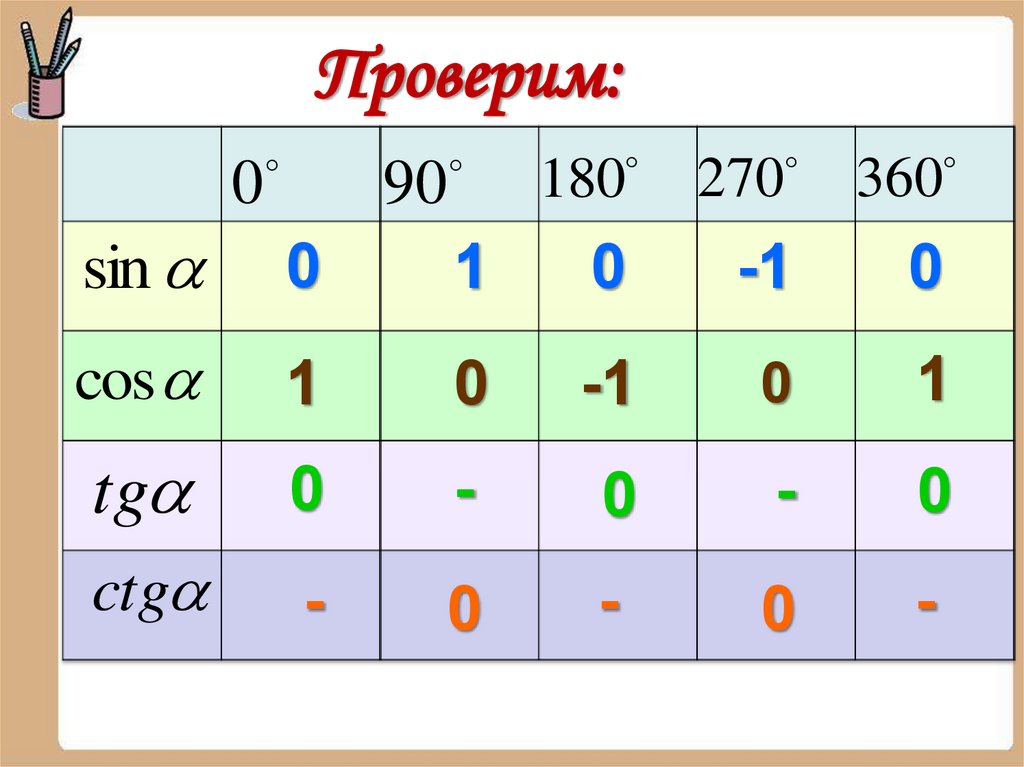
Проверим:
0
90
180
270
360
sin
0
1
0
-1
0
cos
1
0
-1
0
1
tg
0
-
0
-
0
ctg
-
0
-
0
-

9.

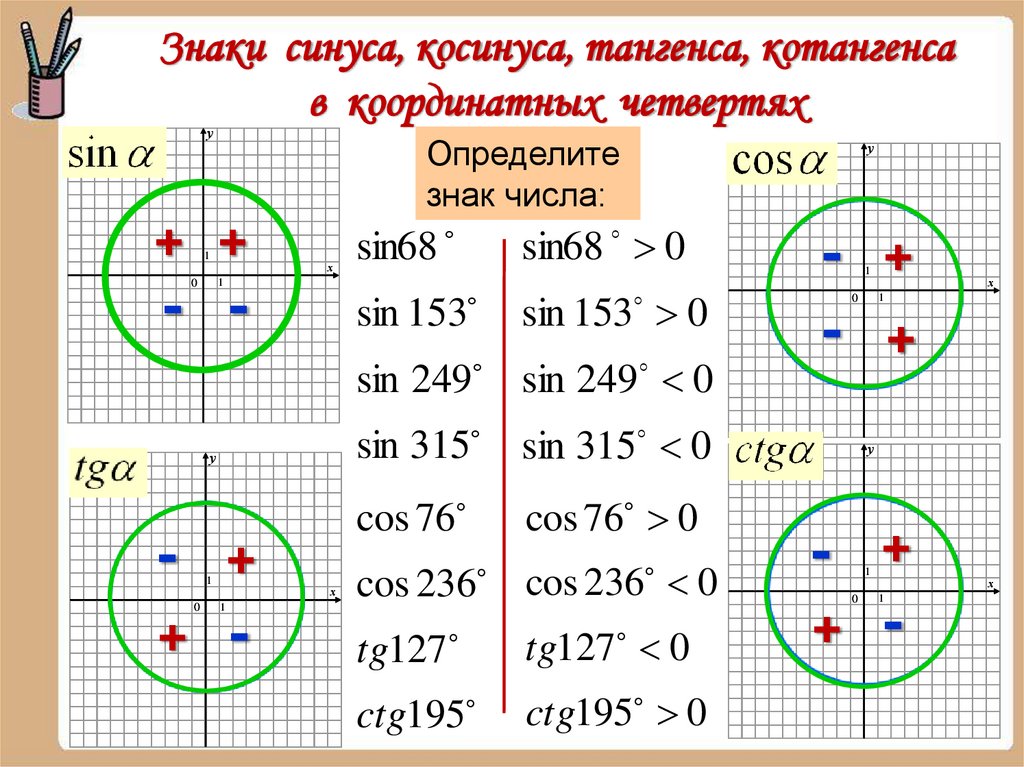
Знаки синуса, косинуса, тангенса, котангенса
в координатных четвертях
у
Определите
знак числа:
+ +
1
х
1
0
- -
у
sin68
sin68 0
sin 153
sin 153 0
sin 249 sin 249 0
у
- +
+ 1
0
1
х
sin 315
sin 315 0
cos 76
cos 76 0
cos 236
tg127
ctg195
cos 236 0
tg127 0
ctg195 0
- +
- +
1
х
1
0
у
- +
+ 1
0
1
х

10.

Письменно решаем № с нечетными числами.

11.

Домашнее задание № 82
Знать табличные значения - слайд 10, знать знаки по
четвертям – слайд 11, знать значения в «главных
точках» - слайд 12. Решить № с четными числами.