Числовые промежутки (7 класс)

1.

2. Прочитать:

19 < x ≤ 75
10 ≤ x < 72
-1 < x < 20

3.

Укажи мышкой на числа, кратные 5 и удовлетворяющие
неравенству
19 < x ≤ 75
10 19 54
46 64 75
20 43 80
35
19 <
≤ 75
19 <
≤ 75
19 <
≤ 75

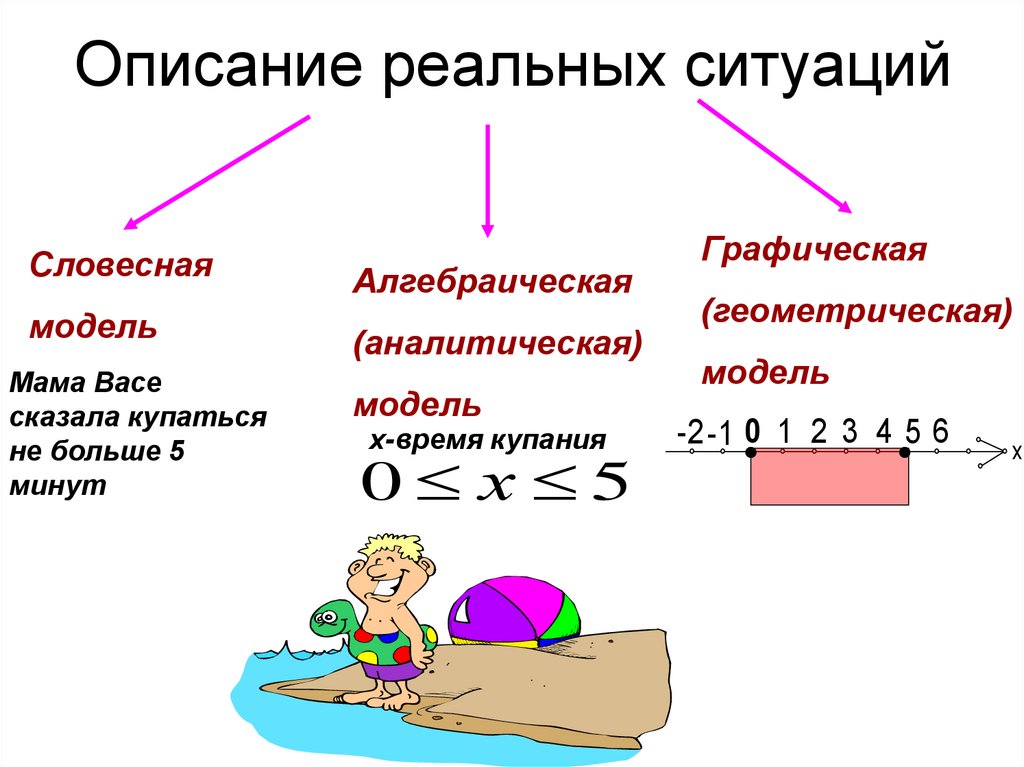
4. Описание реальных ситуаций

Словесная
модель
Мама Васе
сказала купаться
не больше 5
минут
Алгебраическая
(аналитическая)
модель
х-время купания
0 х 5
Графическая
(геометрическая)
модель
-2 -1 0 1 2 3 4 5 6
х

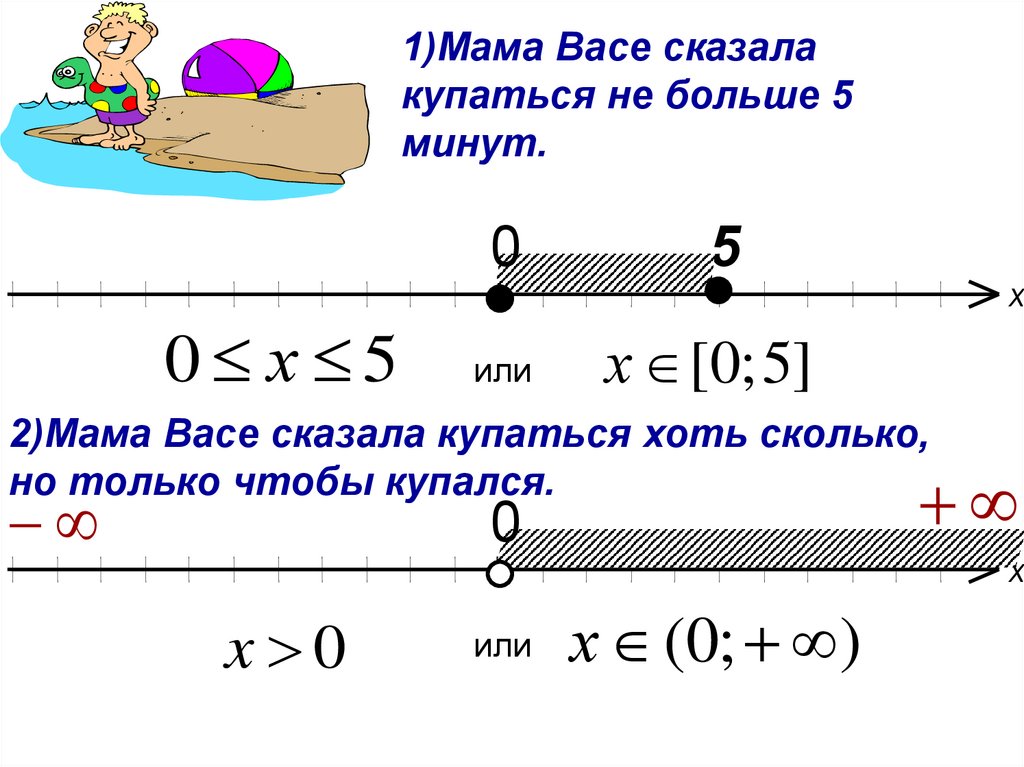
5. 1)Мама Васе сказала купаться не больше 5 минут.

0 х 5
0
5
или
х [0; 5]
х
2)Мама Васе сказала купаться хоть сколько,
но только чтобы купался.
0
x 0
или
х
õ (0; )

6.

«Бесконечность».
Знак
для указания
неограниченного возрастания числа
был введен Джоном Валлисом(1655).
Предполагают, что Валлис
использовал римский символ
,
означавший 1 000. Знак стал
общепринятым уже с XVIII в., хотя
время от времени употреблялись и
другие обозначения
(например,
или 0 – 0)
1616-1703гг

7. 1)Мама Васе сказала купаться не больше 5 минут.

0 х 5
0
5
или
х [0; 5]
х
2)Мама Васе сказала купаться хоть сколько,
но только чтобы купался.
0
x 0
или
х
х (0; )

8.

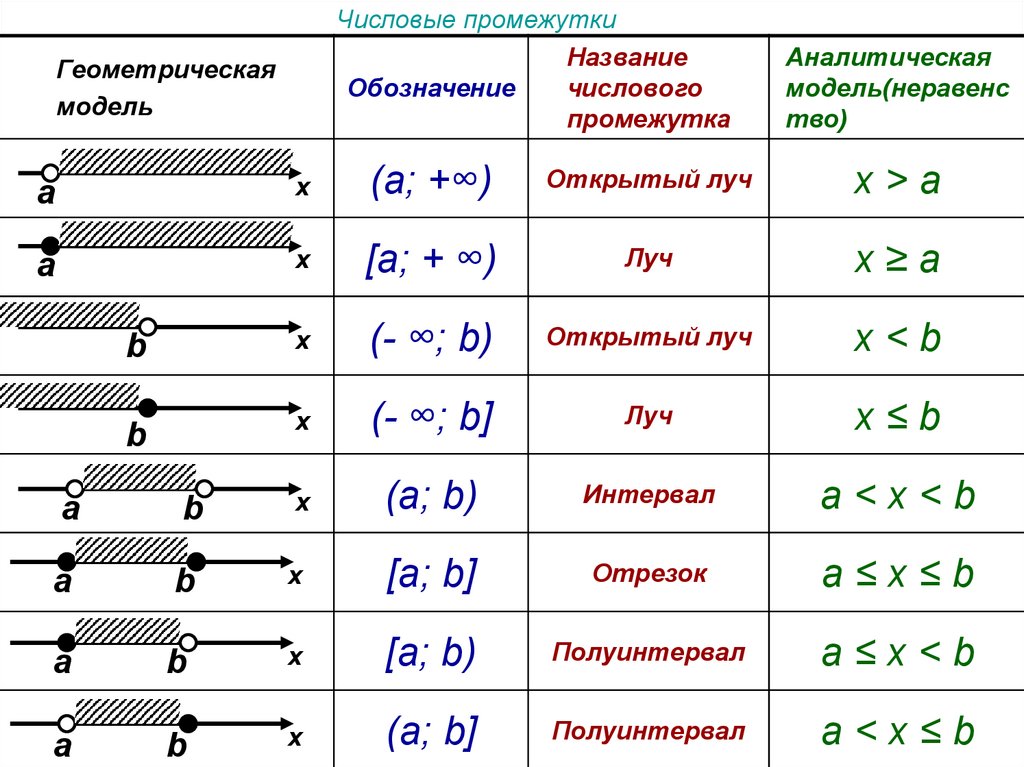
Числовые промежутки
Название
Обозначение
числового
промежутка
Геометрическая
модель
Аналитическая
модель(неравенс
тво)
a
x
(а; +∞)
Открытый луч
х>a
a
x
[a; + ∞)
Луч
х≥а
b
x
(- ∞; b)
Открытый луч
х<b
b
x
(- ∞; b]
Луч
x≤b
a
b
x
(а; b)
Интервал
a<x<b
a
b
x
[a; b]
Отрезок
a≤x≤b
a
b
x
[a; b)
Полуинтервал
a≤x<b
a
b
x
(a; b]
Полуинтервал
a<x≤b

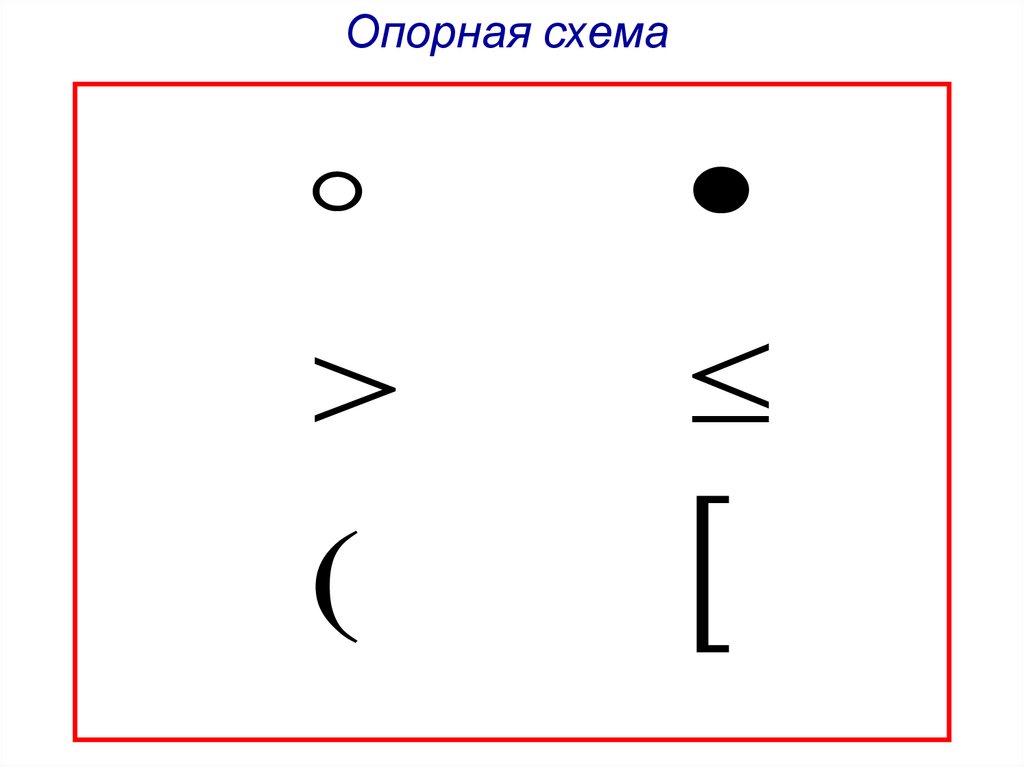
9.

Опорная схема
(

10.

№1
Открытый луч
х 2
IIIIIIIIIIIIIIIIII
2
х (2; )
х

11.

№2
луч
х 3
IIIIIIIIIIIIIIIIIIII
-3
х ( ; 3
х

12.

№3
Отрезок
11 х 10
IIIIIIIIIIIIIII
-11
-10
х [ 11; 10]
х

13.

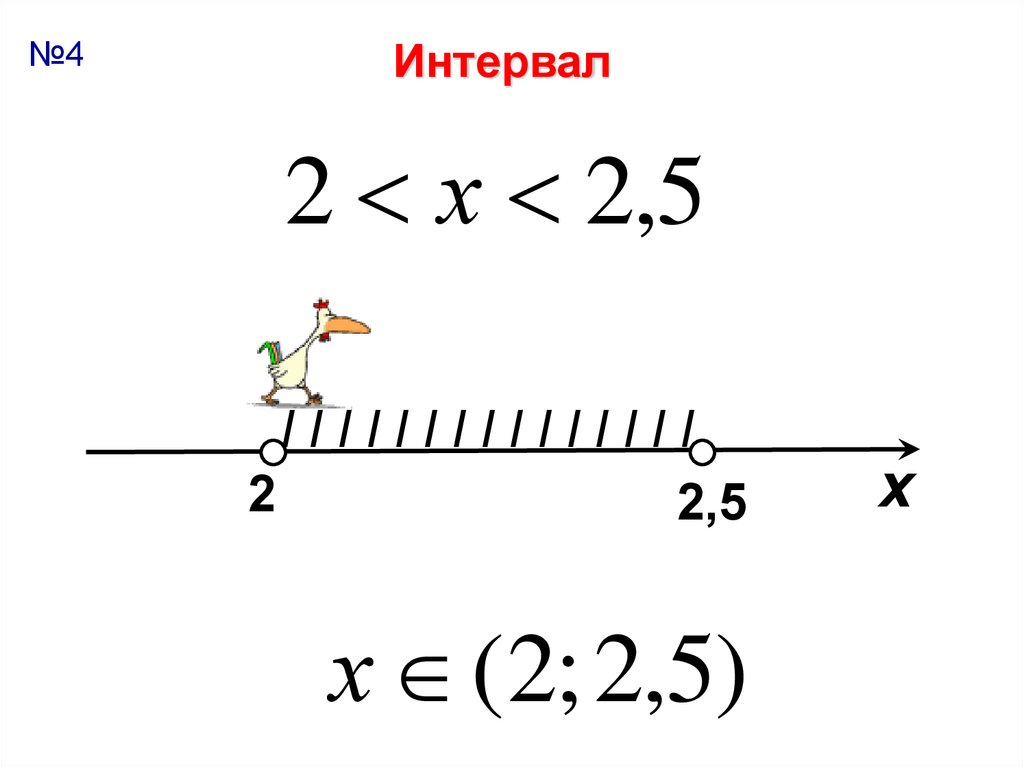
№4
Интервал
2 х 2,5
IIIIIIIIIIIIIII
2
2,5
х (2; 2,5)
х

14.

№5
Полуинтервал
7 х 6
IIIIIIIIIIIIIIIIII
-7
-6
х ( 7; 6]
х

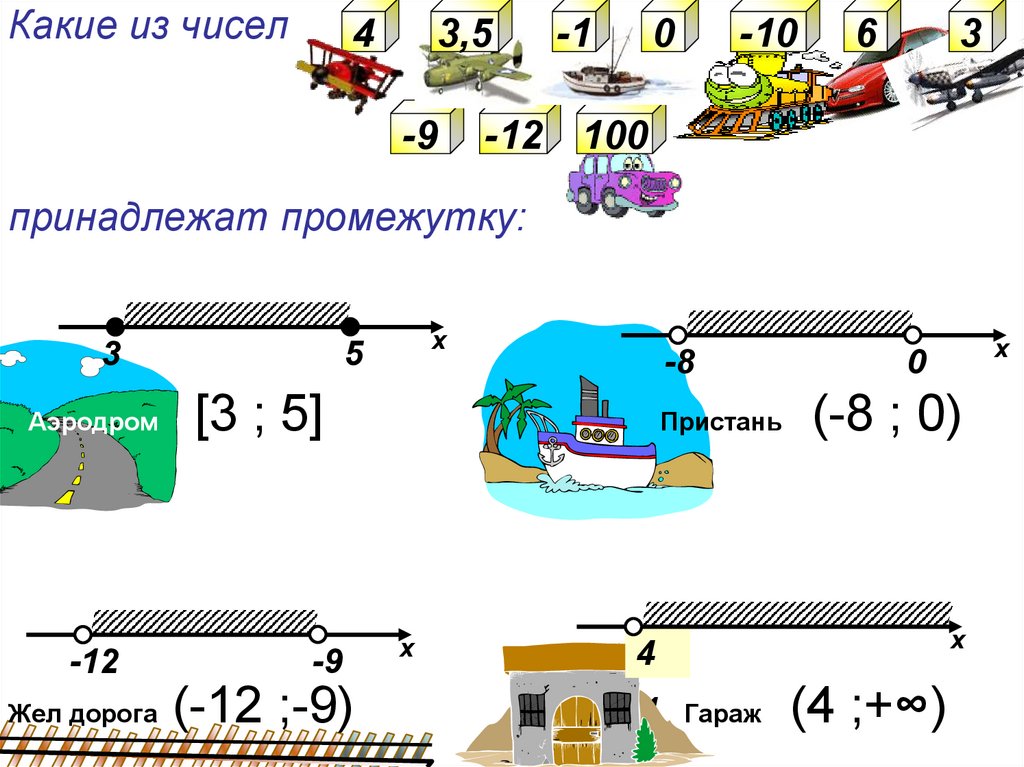
15. Какие из чисел принадлежат промежутку:

Какие из чисел
4
3,5
-9
-1
0
-10
6
3
-12 100
принадлежат промежутку:
3
Аэродром
-12
Жел дорога
x
5
-8
[3 ; 5]
-9
(-12 ;-9)
Пристань
x
(-8 ; 0)
x
4
1
x
0
Гараж
(4 ;+∞)

16.

Самостоятельная работа
Установите соответствия, соединив ячейки числами
Геометрическая
модель
Название
числового
промежутка
Аналитическая
модель(неравенс
тво)
Интервал
2
Обозначение
1
a
b
(- ∞; b]
x
2
3
a
x
a
x
b
(a; b]
(- ∞; b)
4
x
b
5
a
b
[a; b)
x
6
[a; b]
x
a
7
a
b
(а; b)
x
8
b
(а; +∞)
x
[a; + ∞)
5
3
Полуинтервал
1
6
8
7
5
Открытый луч
Полуинтервал
8
4
1
7
Открытый луч
Отрезок
2
Луч
6
4
Луч
3
х≥а
a≤x≤b
х<b
a<x<b
x≤b
a≤x<b
х>a
a<x≤b