Похожие презентации:
Методы решения тригонометрических уравнений, сравнивать уравнения и находить отличия и уметь их решать
1.
Знать и уметь• Методы решения тригонометрических
уравнений, сравнивать уравнения и
находить отличия и уметь их решать.
2.
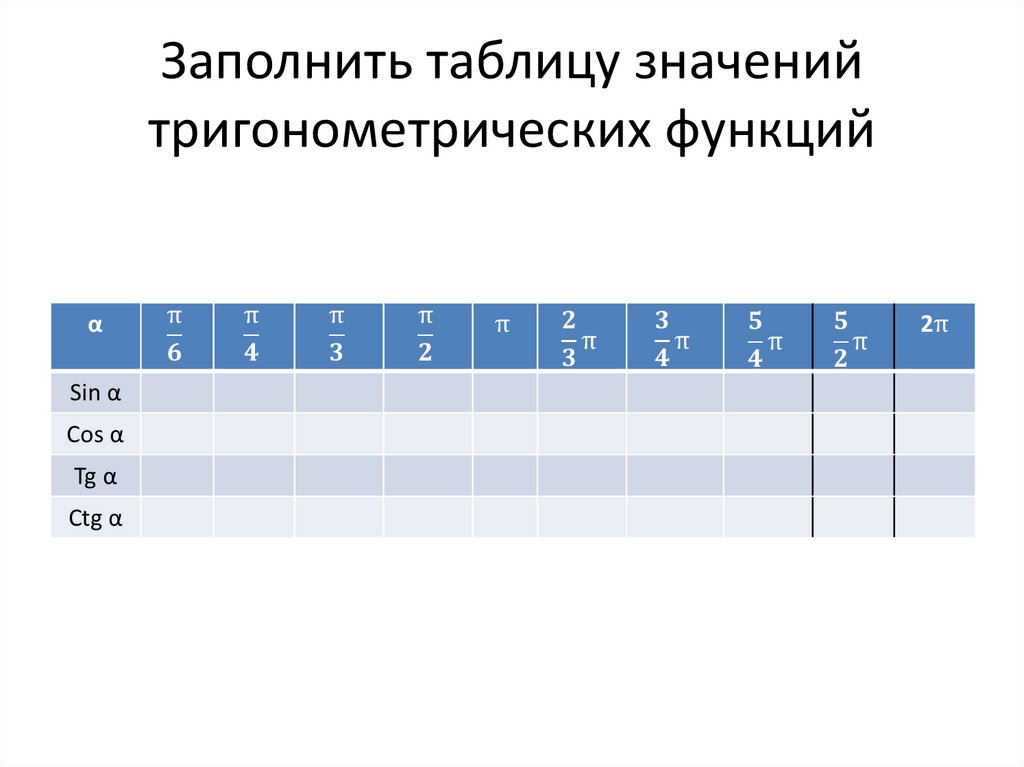
Заполнить таблицу значенийтригонометрических функций
α
Sin α
Cos α
Tg α
Ctg α
3.
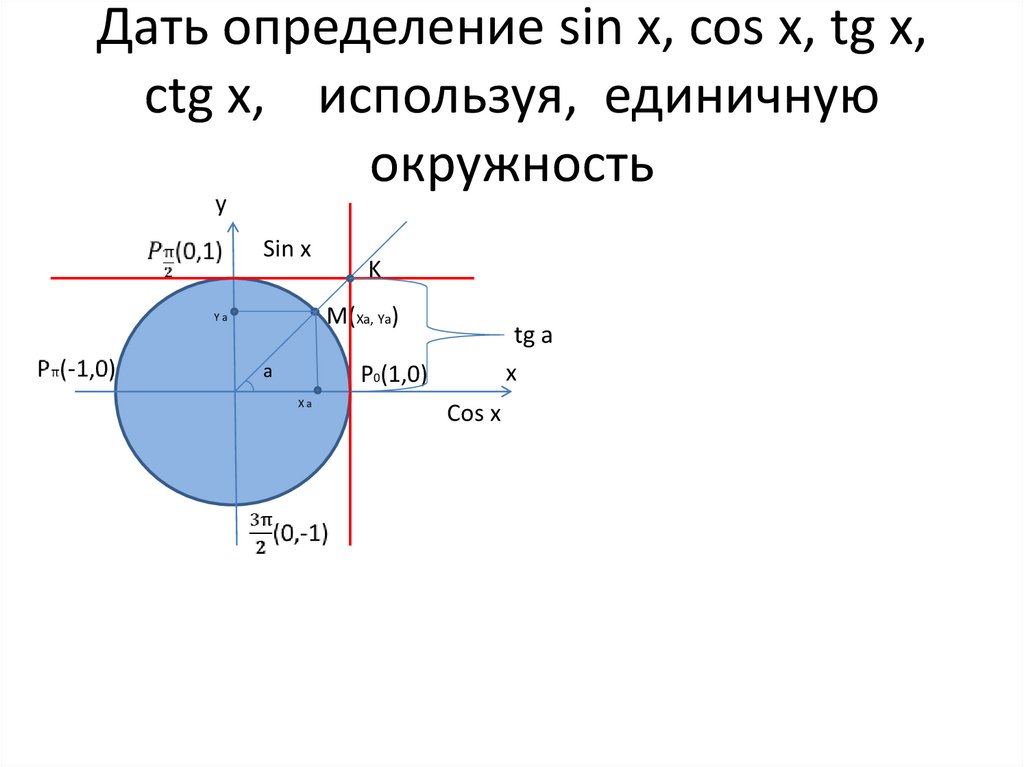
Дать определение sin x, cos x, tg x,ctg x, используя, единичную
окружность
y
Sin x
K
M(Xa, Ya)
Ya
a
tg a
x
P0(1,0)
Xa
Cos x
4.
Проверочная работа с цельюподготовки восприятия нового
материала
• Записать формулу решения уравнений
Вариант №1
Вариант №2
• Cos x = a
sin x = a
• При какой значении а уравнения имеет
решения
• Построить единичную окружность укажите на
какой оси откладывается а при решении
уравнения
• Cos x = а
sin x = а
5.
• Дать определения tg x, ctg x, записать формулырешения уравнений в таблицы.
• Написать частные случаи решения уравнений.
6.
Заполнить таблицуЗадание
Формулы для решения
тригонометрических
уравнений
Частные случаи решения
тригонометрических
уравнений
Sin x = A
Sin x = -1
Sin x = 0
Sin x = 1
Cos x = A
cos x = -1
cos x = 0
cos x = 1
Tg x = A
Tg x = 0
Tg x = 1
Tg x = -1
Ctg x = A
сtg x = 0
сtg x = 1
сtg x = -1
Ответы
7.
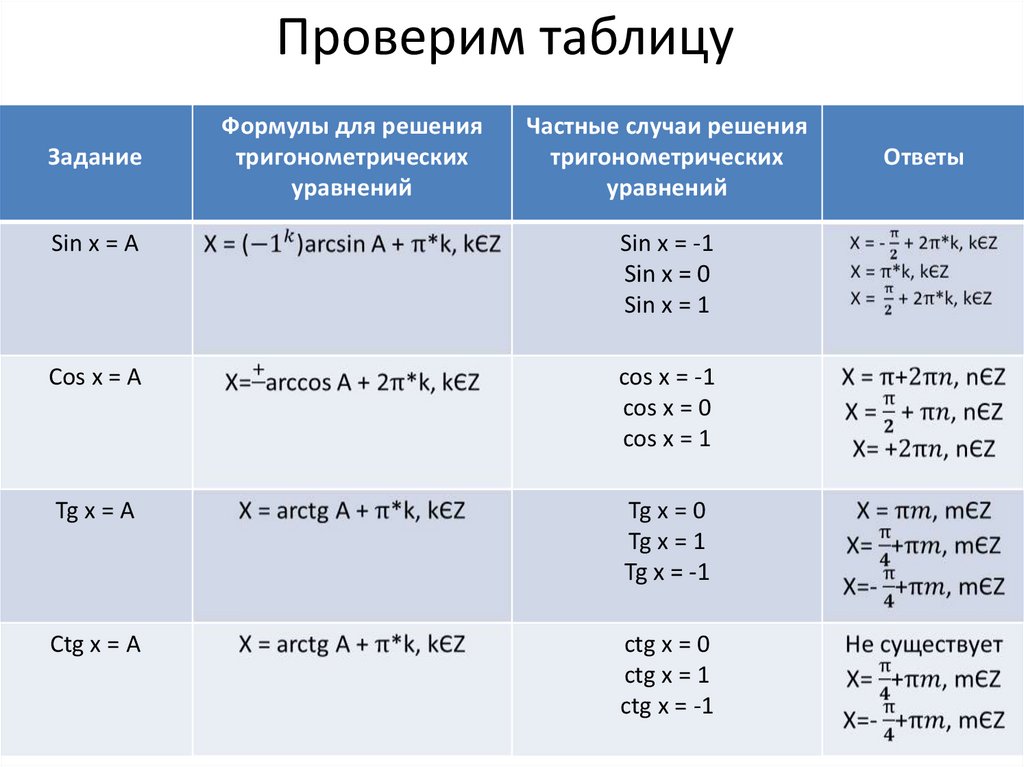
Проверим таблицуЗадание
Формулы для решения
тригонометрических
уравнений
Частные случаи решения
тригонометрических
уравнений
Sin x = A
Sin x = -1
Sin x = 0
Sin x = 1
Cos x = A
cos x = -1
cos x = 0
cos x = 1
Tg x = A
Tg x = 0
Tg x = 1
Tg x = -1
Ctg x = A
сtg x = 0
сtg x = 1
сtg x = -1
Ответы
8.
Задание №3• Дать определение обратных
тригонометрических функций, указать область
определения и область значений функции.
• Что такое arcsin а
arccos а
• В каком промежутке находится значение а
• Что называется arctg а и arcctg а , в к аком
промежутке находятся число а
9.
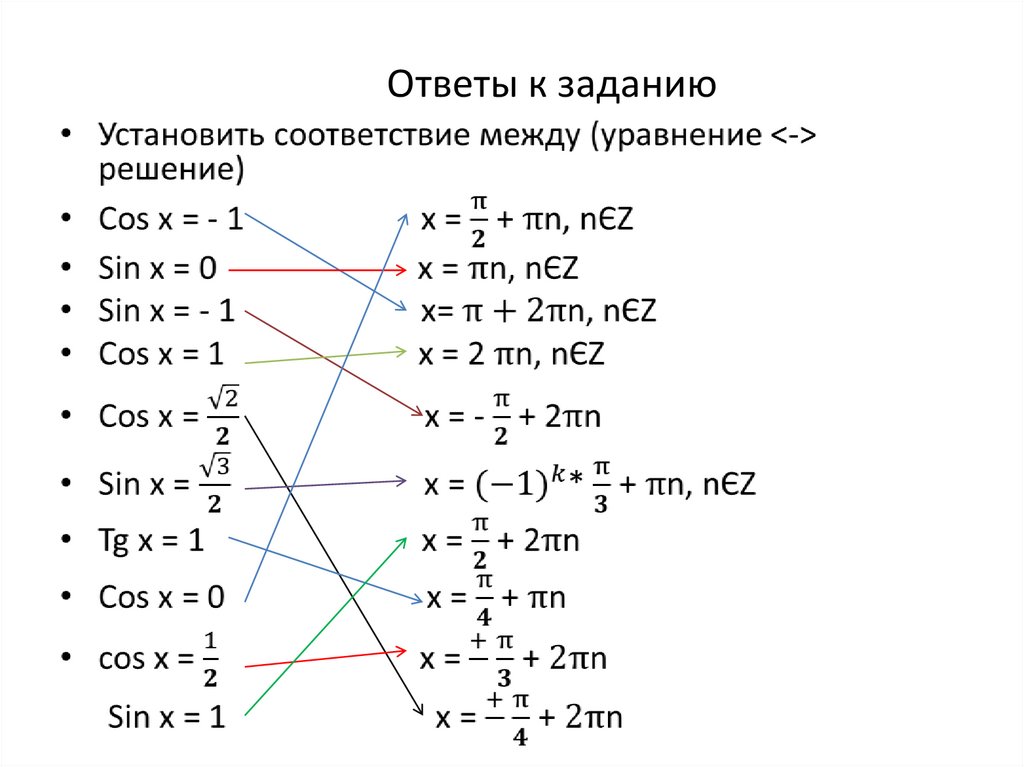
Задание №5 – установитьсоответствие
10.
Ответы к заданию11.
YSin x
x
P0(1,0)
Cos x






 Математика
Математика








