Радианная мера угла

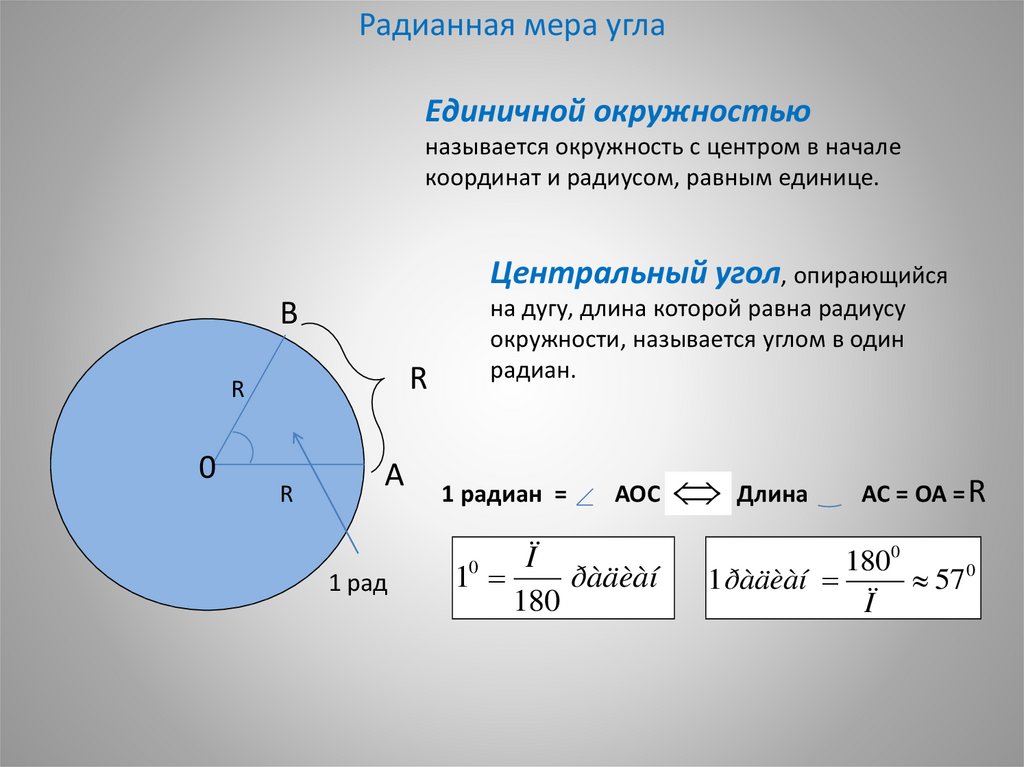
Радианная мера угла
Единичной окружностью
называется окружность с центром в начале
координат и радиусом, равным единице.
Центральный угол, опирающийся
на дугу, длина которой равна радиусу
окружности, называется углом в один
радиан.
В
R
R
0
R
А
1 рад
1 радиан =
АОС
Ï
1
ðàäèàí
180
0
Длина
АС = ОА = R
1800
1 ðàäèàí
57 0
Ï

3.

Тригонометрические функции угла и числового аргумента
Определение тригонометрических функций
Через единичную
Через произвольную
окружность (радиус равен 1) окружность
Р (х;у)
у
0
В
Р (х;у)
у
Через прямоугольный
треугольник (для острых
углов
c
х
0
a
х
А
b
Sin a = y - ордината точки Р
Соs a = х - абсцисса точки Р
ó sin a
õ cos a
b cos a
ctg
a sin a
tg
ó
R
õ
cos
R
ó
tg
õ
õ
ctg
ó
sin
à
ñ
b
cos
c
a
tg
b
b
ctg
a
sin
С

4.

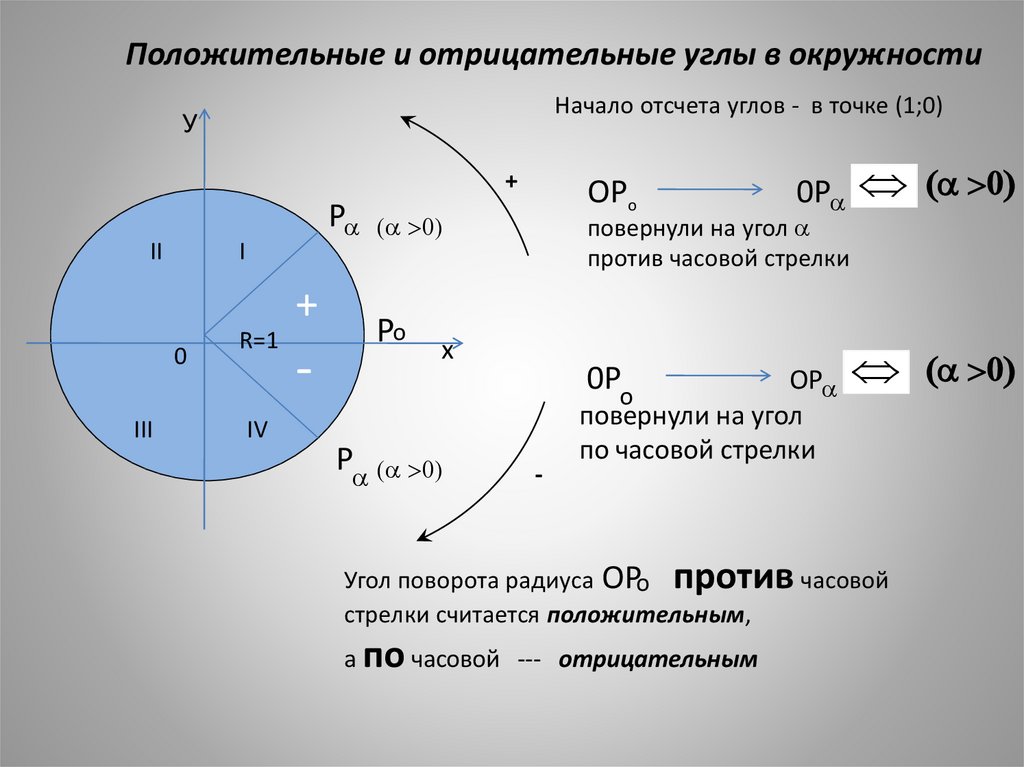
Положительные и отрицательные углы в окружности
Начало отсчета углов - в точке (1;0)
У
+
I
0
III
R=1
+
-
( >0)
Ро х
0Ро
IV
Р ( >0)
0Р
( >0)
повернули на угол
против часовой стрелки
-
II
Р
ОРо
ОР
повернули на угол
по часовой стрелки
( >0)
Угол поворота радиуса ОРо против часовой
стрелки считается положительным,
а по часовой --- отрицательным

5.

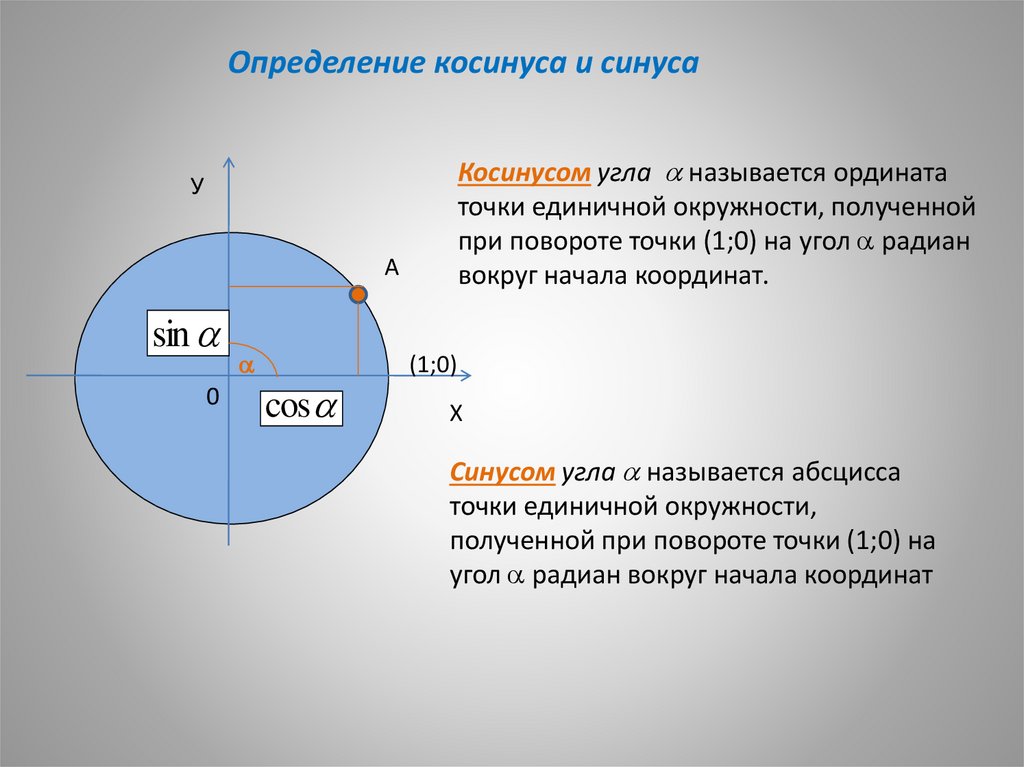
Определение косинуса и синуса
Косинусом угла называется ордината
точки единичной окружности, полученной
при повороте точки (1;0) на угол радиан
вокруг начала координат.
У
А
sin
0
cos
(1;0)
Х
Синусом угла называется абсцисса
точки единичной окружности,
полученной при повороте точки (1;0) на
угол радиан вокруг начала координат

6.

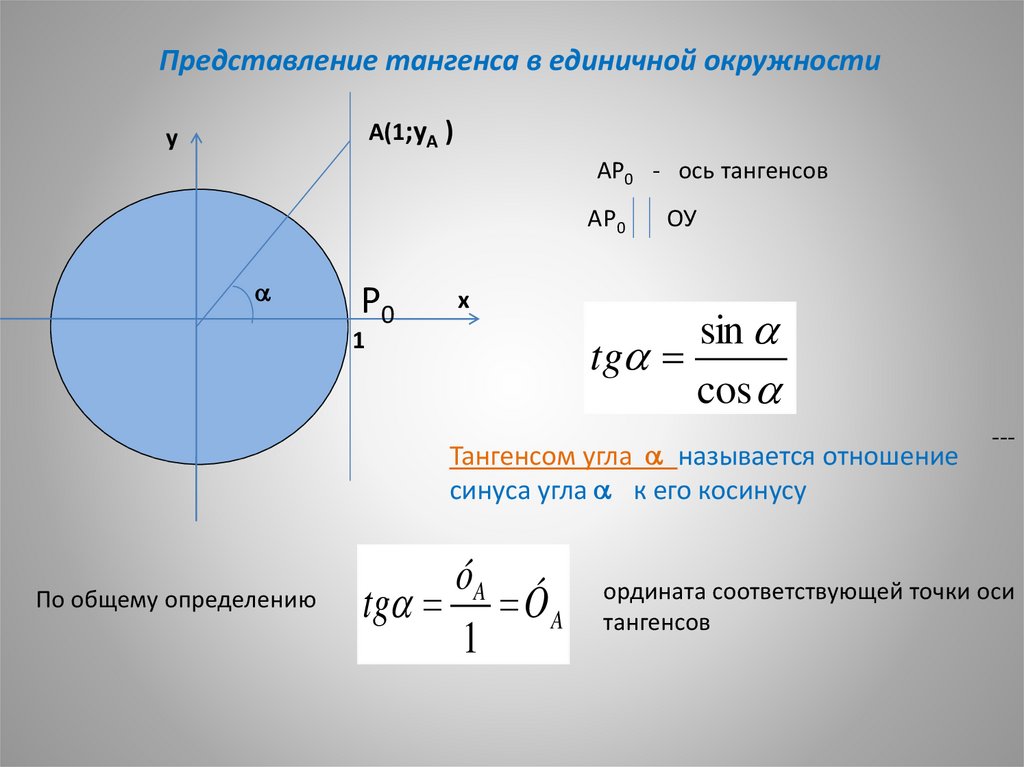
Представление тангенса в единичной окружности
А(1;уА )
у
АР0 - ось тангенсов
А Р0
Р0
х
1
ОУ
sin
tg
cos
Тангенсом угла называется отношение
синуса угла к его косинусу
По общему определению
óA
tg Ó A
1
---
ордината соответствующей точки оси
тангенсов

7.

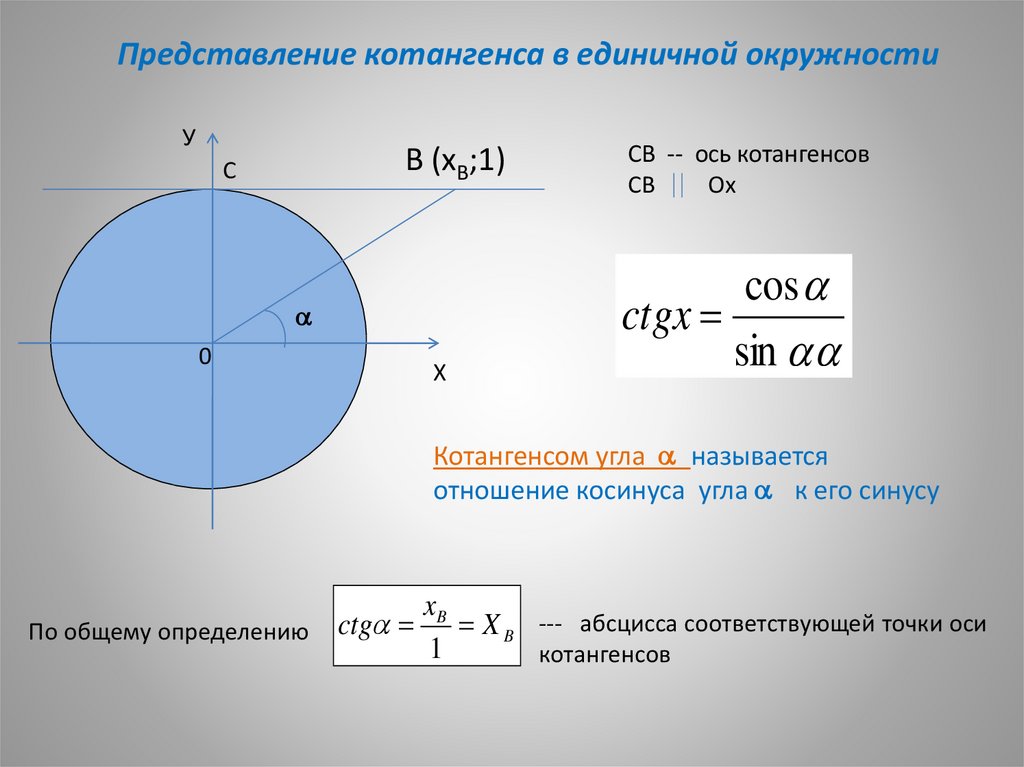
Представление котангенса в единичной окружности
У
В (хВ;1)
С
0
Х
СВ -- ось котангенсов
СВ
Ох
cos
ctgx
sin
Котангенсом угла называется
отношение косинуса угла к его синусу
По общему определению ctg
xB
X B --- абсцисса соответствующей точки оси
1
котангенсов

8.

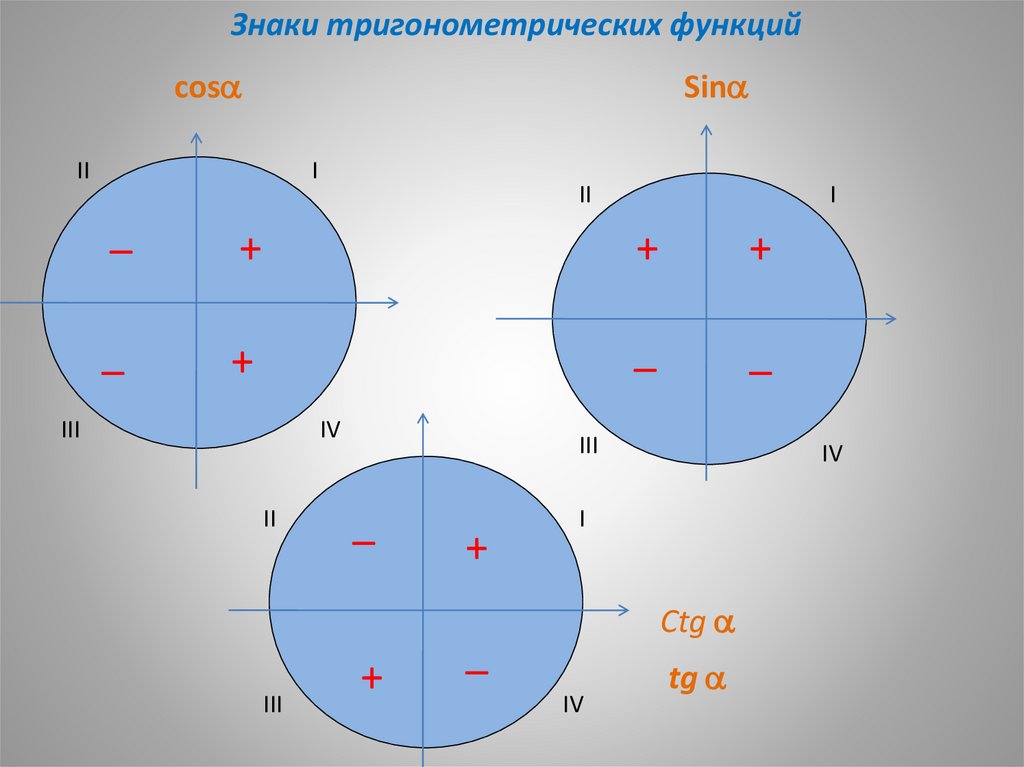
Знаки тригонометрических функций
cos
Sin
II
I
+
_
+
I
+
+
_
_
_
II
III
IV
II
III
III
_
+
+
IV
I
Сtg
_
IV
tg

9.

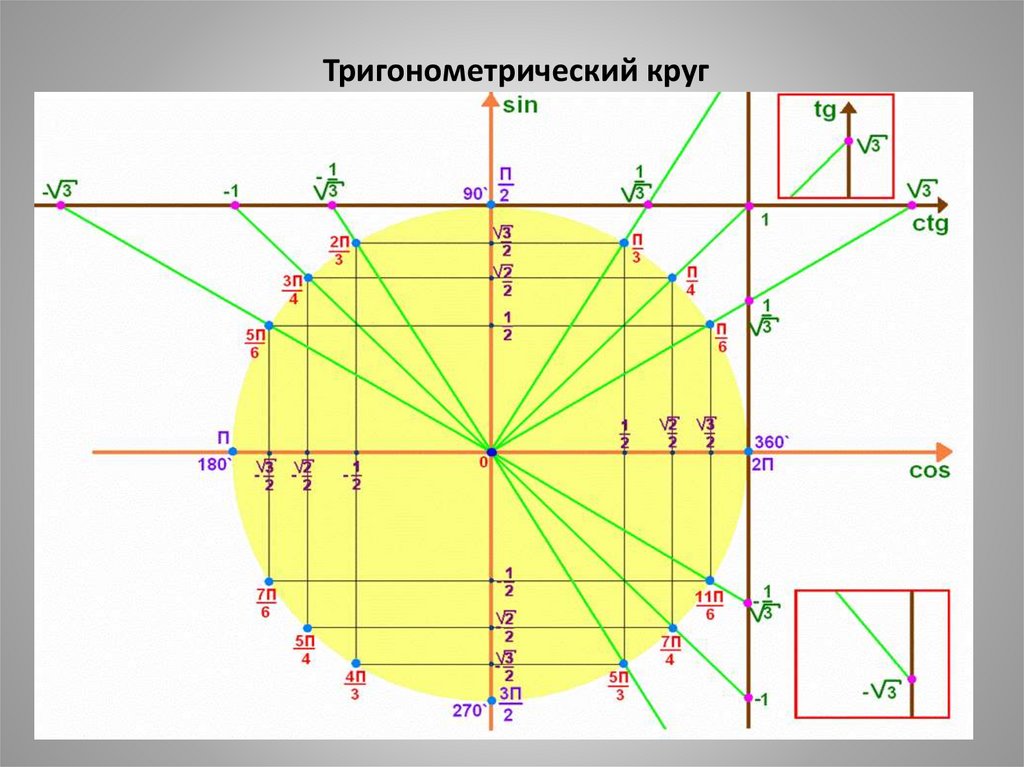
Тригонометрический круг

10.

Основные значения тригонометрических функций углов
I четверти приведены в таблице.

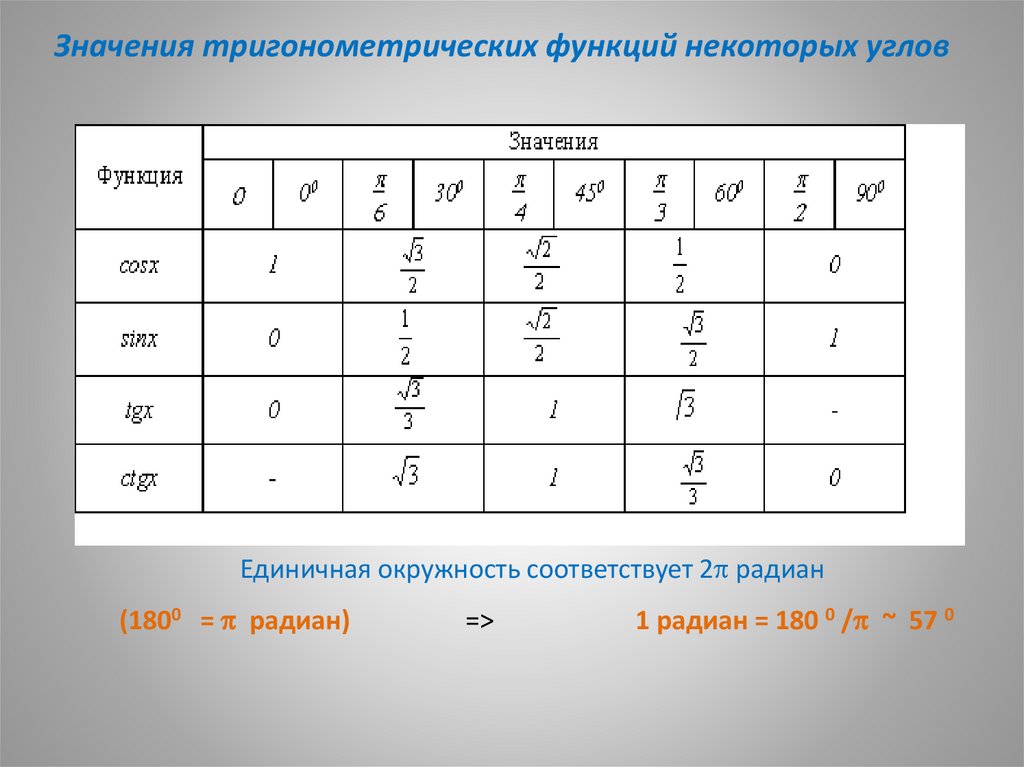
11.

Значения тригонометрических функций некоторых углов
Единичная окружность соответствует 2p радиан
(1800 = p радиан)
=>
1 радиан = 180 0 /p ~ 57 0

12. Свойства тригонометрических функций

Четность и нечетность
cos( ) cos
Косинус- четная функция
sin( ) sin
tg ( ) tg
ctg ( ) ctg
Синус, тангенс, котангенс –
нечетные функции
Периодичность
sin , cos
Тогда
-- период
sin( x 2 Ïê ) sin x
cos( x 2 Ïê ) sin x, ê
tg , ctg --- период
Тогда
Т = 2П
Т = П
tg ( x Ïê ) tgx
ctg ( x Ïê ) ctgx, ê

13.

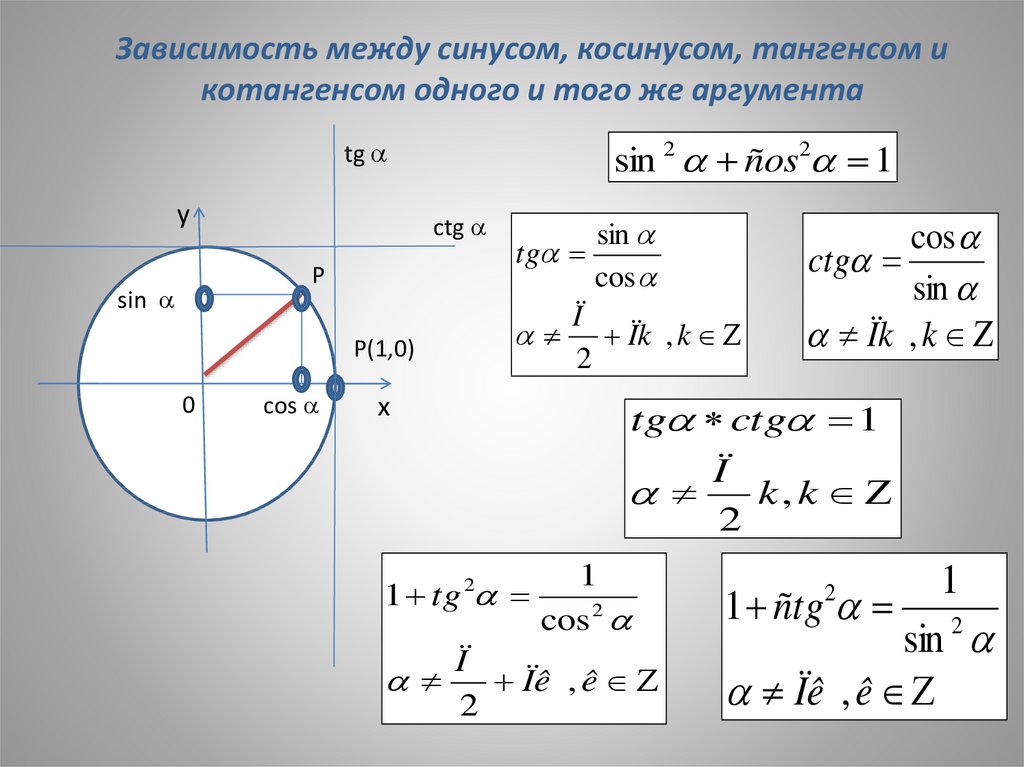
Зависимость между синусом, косинусом, тангенсом и
котангенсом одного и того же аргумента
sin 2 ños2 1
tg
у
ctg
Р
sin
Р(1,0)
0
cos
tg
sin
cos
Ï
Ïk , k
2
cos
ctg
sin
Ïk , k
tg ctg 1
Ï
k, k
2
х
1
1 tg
cos 2
Ï
Ïê , ê
2
2
1
1 ñtg 2
sin
Ïê , ê
2

14.

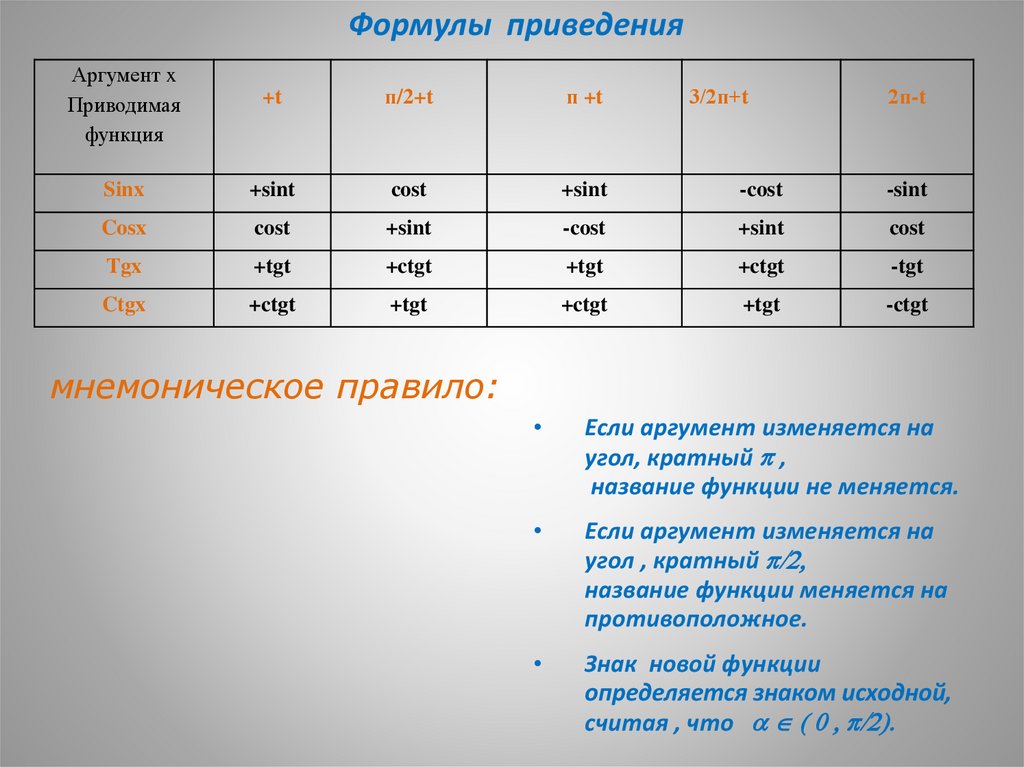
Формулы приведения
Аргумент x
Приводимая
функция
+t
п/2+t
п +t
Sinx
+sint
cost
+sint
-cost
-sint
Cosx
cost
+sint
-cost
+sint
cost
Tgx
+tgt
+ctgt
+tgt
+ctgt
-tgt
Ctgx
+ctgt
+tgt
+ctgt
+tgt
-ctgt
3/2п+t
2п-t
мнемоническое правило:
Если аргумент изменяется на
угол, кратный p ,
название функции не меняется.
Если аргумент изменяется на
угол , кратный p/2,
название функции меняется на
противоположное.
Знак новой функции
определяется знаком исходной,
считая , что ( 0 , p/2).

English Русский Правила