Решение заданий части С1

1.

Решение заданий
части С1.
Подготовила
учитель математики
МКОУ «Хотьковская СОШ»
Наталья Николаевна Коломина
2016г.

2.

С1
Подсказка
Решите уравнение:
2 3 х х 2 2( х 1 ) х
Данное уравнение после возведения в квадрат будет иметь
четвёртую степень. Ничего не упрощает и обозначение корня
через новую переменную, создающее в уравнении четвёртую
степень сразу, безо всякого возведения.
Зато левая часть уравнения раскладывается на множители, один из
которых совпадает с множителем, стоящим перед корнем в правой
части. Этим нужно воспользоваться.
Посмотреть решение

3.

С1
Подсказка
Решите уравнение:
sin x sin x cos x
Имеющийся в уравнении модуль раскроем по определению,
причём наиболее приятный случай его равенства нулю
рассмотрим отдельно.
Посмотреть решение

4.

С1
Подсказка
Решите уравнение:
4 cos x ctgx 4 ctgx sin x 0
Представив котангенс в виде дроби, приведём левую часть
уравнения к общему знаменателю.
Посмотреть решение

5.

С1
Подсказка
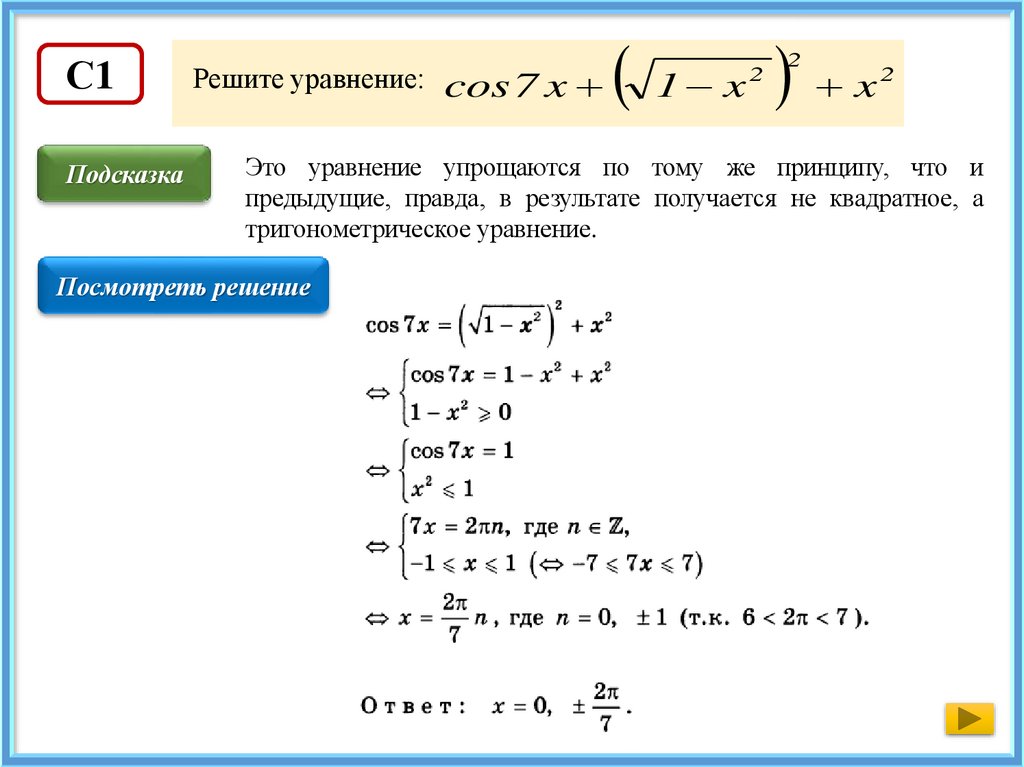
Решите уравнение: cos 7 x
1 x x
2
2
2
Это уравнение упрощаются по тому же принципу, что и
предыдущие, правда, в результате получается не квадратное, а
тригонометрическое уравнение.
Посмотреть решение

6.

С1
Подсказка
Решите уравнение:
sin 2 x tgx 1 3 sin x
Первое слагаемое в данном уравнении упрощается за счёт его
сокращения на выражение cos x, неявно фигурирующее и в
числителе, и в знаменателе. После этого уравнение становится
квадратным относительно переменной sin x.
Посмотреть решение

7.

С1
Посмотреть решение

8.

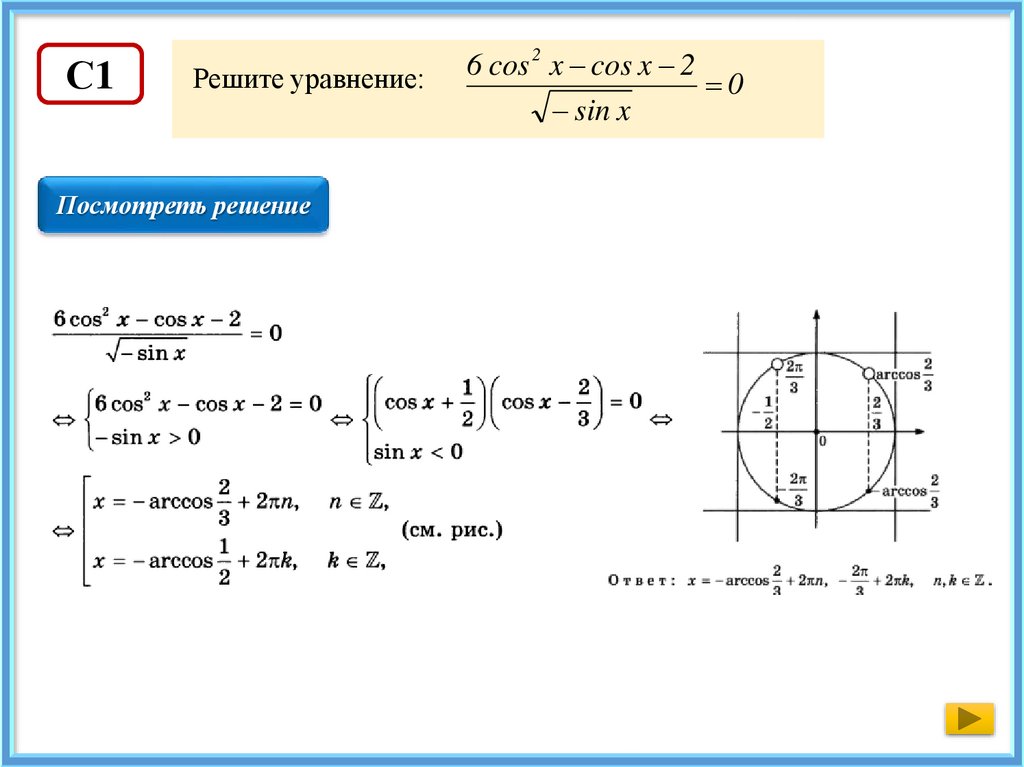
С1
Решите уравнение:
Посмотреть решение
6 cos 2 x cos x 2
0
sin x

9.

С1
Посмотреть решение

10.

С1
Подсказка
Решите уравнение:
7 tg x cos 2 x 3 sin 2 x 1
На первый взгляд, совершенно непонятно, как решать такое
уравнение – слишком много в нём самых разных
тригонометрических функций. А значит, прежде всего, нужно
попытаться уменьшить их количество. Для этого распишем
тангенс через синус и косинус. То же проделаем с синусом
двойного угла, а заодно и с единицей.
Посмотреть решение

11.

С1
Подсказка
Решите уравнение: 32 х 3 3 3 х 1 625 х 2 600 х 7
Необходимо привести уравнение к виду, в котором и левая, и правая
части представляют собой степени одного и того же фиксированного
числа. Затем отбросить полученные одинаковые основания этих
степеней. Заметим, что в обеих частях уравнения основания всех
степеней порождаются числами 2, 3, 5 или их комбинациями.
Посмотреть решение

12.

С1
Подсказка
Решите уравнение:
6
3
4 log 2 2
8 3 log 2 2
2
x
5
x
1
В результате приведения к общему знаменателю под знаками
логарифмов в уравнении появляются подобные члены.
Посмотреть решение

13.

С1
Решите уравнение:
Посмотреть решение
9 4x x 4 4x 3

14.

С1
Подсказка
Решите уравнение:
13
4
2 log 3 3 x
log x 3
В этом уравнении довольно быстро угадывается нова переменная
l log 3 x
Посмотреть решение

15.

С1
Подсказка
Решите уравнение: log 81 ( 15 7 x ) log 3 x 9 1
Наиболее существенное упрощение данного уравнения даёт переход к
новому основанию – лучше всего к основанию 3.
Посмотреть решение

16.

С1
Подсказка
Решите уравнение: log x 5 log 2 x 31
2
2
25 x x
2
2
2
Возведённый в квадрат корень даёт подкоренное выражение. В
результате этого уравнение резко упрощается и становится
квадратным относительно переменной log 2 x
Посмотреть решение

17.

Ссылки на изображения:
http://asosh07.ucoz.ru/GO/egeh_2017.jpg
Источник:
ЕГЭ: 1000 задач с ответами и решениями по математике. Все задания
группы С / И.Н.Сергеев, В.С.Панферов.- М.: Издательство «Экзамен», 2012.