Тригономентрия. Основные определения

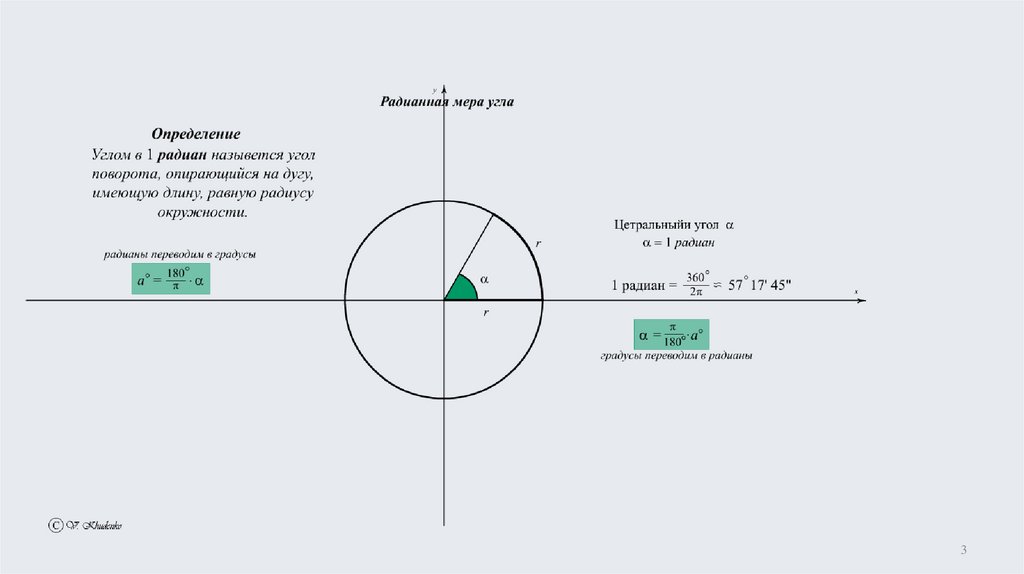
1.

Тригонометрия

2.

Основные определения
2

3.

3

4.

1
4

5.

5

6.

6

7.

7

8.

8

9.

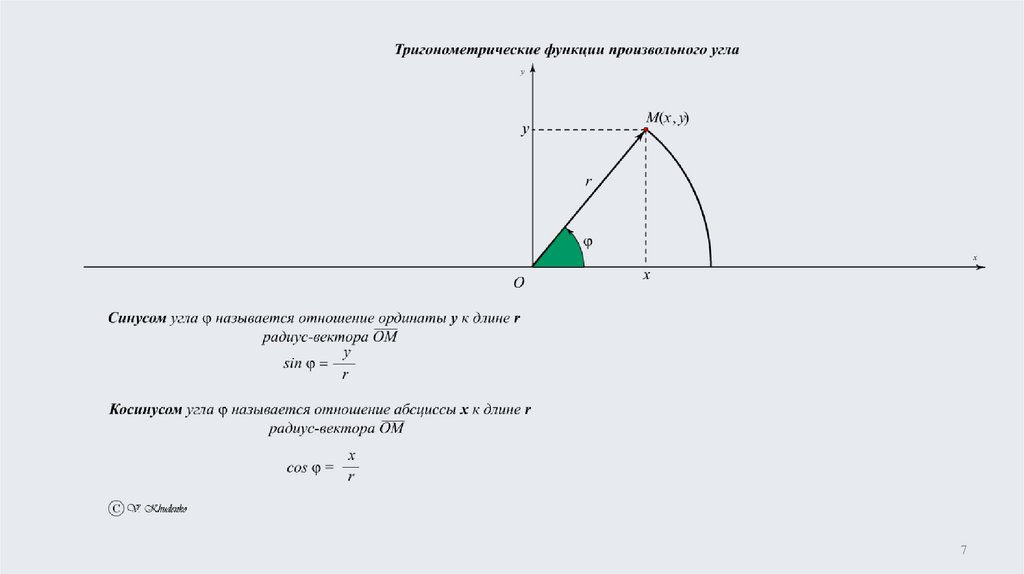
§1.Основные определения
sin
y
r
9

10.

x
cos
r
10

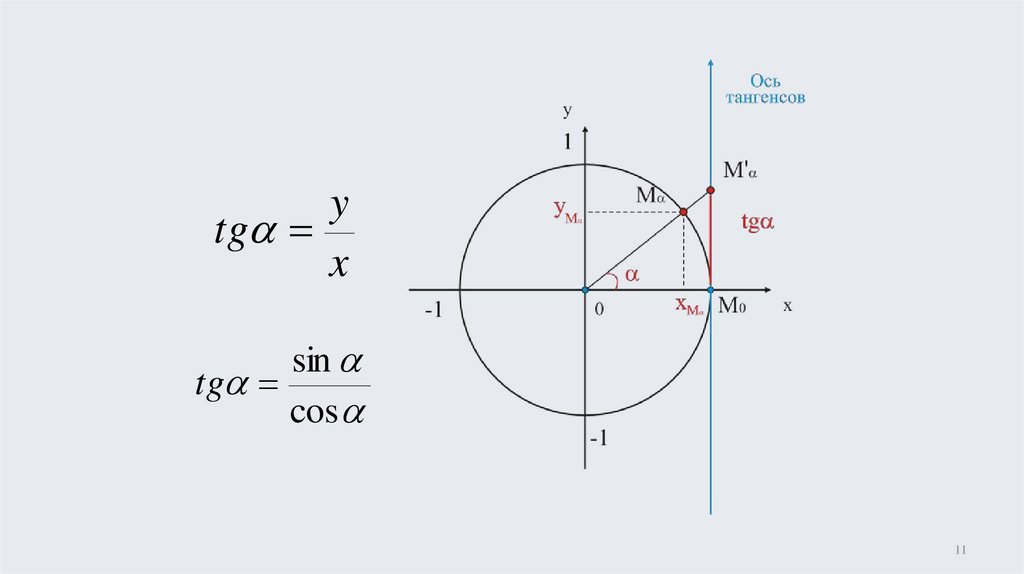
11.

y
tg
x
sin
tg
cos
11

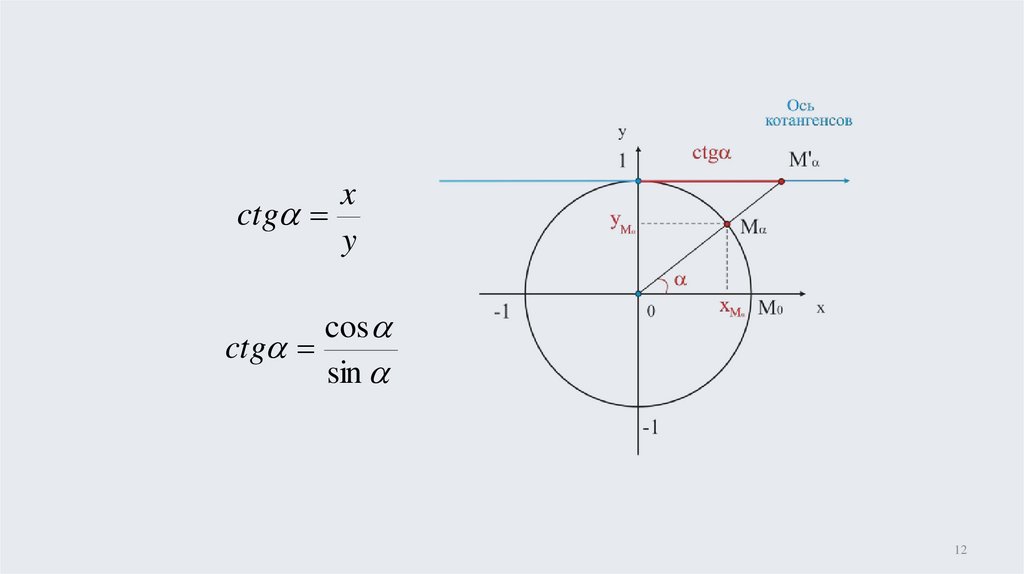
12.

x
ctg
y
cos
ctg
sin
12

13.

Основные определения
13

14.

§2. Тригонометрические формулы одного
аргумента
sin cos 1
2
2
Из теоремы Пифагора следует, что
ОB2+BM2=OM2 x2+y2=r2
2
2
x y
1
r r
cos sin 1 (2.1)
2
2
14

15.

Непосредственно из определений следуют
соотношения
(2.2)
tg ctg 1
Из основного тригонометрического
тождества следует, что
1
2
(2.3)
1 tg
2
cos
1
1 ctg 2
sin
2
(2.4)
Докажем равенство (2.3)
1
sin 2
1
cos2 sin 2
2
1 tg 1
cos2
cos 2
cos2
15

16.

Из основного тригонометрического
тождества получаем,
2
cos 1 sin
тогда из определения тангенса
sin
tg
n, n Z
для
1 sin
2
2
(2.5)
(2.6)
В формулах (2.5), (2.6) «+» ставим, если угол
из I или IV четвертей (там, где
положителен косинус), в остальных
случаях ставим минус.
16

17.

Аналогично
2
(2.7)
n, n Z
(2.8)
sin 1 cos
и
1 cos2
tg
cos
для
2
В формулах (2.7), (2.8) «+» ставим, если угол
из I или II четвертей (там, где
положителен sin ), в остальных случаях
ставим минус.
17

18.

Из формул (2.3), (2.4) следует
1
cos
1 tg 2
(2.9)
1
sin
1 ctg 2
(2.10)
2
2
§3 Формулы приведения
Формулами приведения называются
тождества, связывающие
тригонометрические функции аргументов
18

19.

2
, ,
3
2
с функциями аргумента .
Первая группа:
sin cos ,
2
sin cos ,
2
cos sin ,
2
cos sin ,
2
tg ctg ,
2
(3.1)
tg ctg ,
2
ctg tg
2
ctg tg
2
19

20.

Вторая группа:
sin sin ,
sin sin ,
cos cos ,
cos cos ,
(3.2)
tg tg ,
tg tg ,
ctg ctg ,
ctg ctg .
20

21.

Третья группа
3
sin
cos ,
2
3
sin
cos ,
2
3
cos
sin ,
2
3
cos
sin ,
2
(3.3)
3
tg
ctg ,
2
3
tg
ctg ,
2
3
ctg
tg ,
2
3
ctg
tg .
2
21

22.

Правило для определения названия функции
если откладывается от горизонтального
диаметра ( , вторая группа формул), то
название приводимой функции не меняется
если же откладывается от
горизонтального диаметра
3
или
2
2
(первая и третья группа формул), то
название приводимой функции заменятся
на кофункцию
22

23.

Правило для определения знака функции
какой знак + или – имеет приводимая
функция в соответствующей четверти,
такой знак и ставится в правой части
формулы приведения.
23

24.

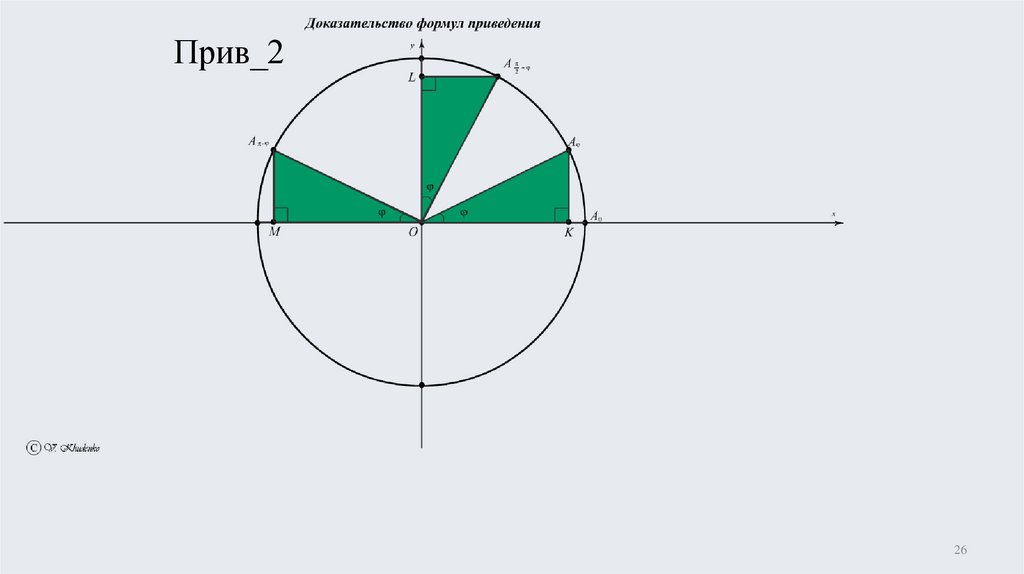
Анимация прив_1
24

25.

Прямоугольные треугольники ONM и OLP
равны по углу и гипотенузе .
Из треугольника ONM находим cos =b; из
треугольника OLP находим cos( + )=-b,
откуда непосредственно следует равенство
cos cos
25

26.

Прив_2
26

27.

Прив_3
27

28.

§4 Тригонометрические формулы суммы и
разности двух углов
Теорема 4.1. Для любых двух углов и
справедлива формула
(4.1)
cos cos cos sin sin
28

29.

Анимация суммы углов
29

30.

Основные определения
30

31.

Основные определения
31

32.

В силу определения тригонометрических
функций координаты этих точек
А(cos ;sin ), B(cos ;sin ). Тогда
координаты двух единичных векторов
OA cos ; sin
OB cos ; sin
32

33.

По определению
OA OB OA OB cos 1 1 cos
(4.2)
По формуле вычисления скалярного
произведения по известным координатам
векторов
OA OB cos cos sin sin (4.3)
Сравнивая правые части формул (4.2) и (4.3),
приходим к справедливости формулы (4.1),
которую в силу четности косинуса можно
записать в виде
cos cos cos sin sin (4.1 )
33

34.

Теорема 4.2. Для любых двух углов
справедлива формула
(4.4)
cos cos cos sin sin
Воспользуемся формулой (4.1 ), где заменим
на – , получаем
cos ( ) cos cos( ) sin sin( )
С учетом четности косинуса и нечетности
синуса получим формулу (4.4)
Следствие Справедлива формула косинуса
двойного угла
(4.5)
cos 2 cos2 sin 2
34

35.

Теорема 4.3. Для любых двух углов
справедлива формула
sin sin cos cos sin
(4.6)
Воспользуемся формулами приведения
sin cos cos
2
2
cos cos sin sin
2
2
sin
sin cos cos sin
cos
Следствие: Имеет место формула синуса
двойного угла
(4.7)
sin 2 2 sin cos
35

36.

Следствие получается при .
Заменив, на – , и учитывая четность и
нечетность функций, получим формулу
синуса разности
sin sin cos cos sin (4.8)
Теорема 4.4. Для любых двух углов и ,
таких что
2k 1 , k Z ;
2
2m 1 , m Z ;
справедлива формула
2
tg tg
tg
1 tg tg
2n 1 , n Z
2
(4.9)
36

37.

По определению тангенса, а также с учетом
формул синуса и косинуса суммы получаем
tg
sin sin cos cos sin
: cos cos
cos cos cos sin sin
: cos cos
sin cos cos sin
sin sin
tg tg
cos cos cos cos
cos cos
cos cos sin sin
sin sin 1 tg tg
1
cos cos cos cos
cos cos
Следствие.
2tg
tg 2
1 tg 2
(4.10)
Теорема 4.5. Для любых двух углов и ,
таких что
2k 1 , k Z ;
2
2m 1
2
2
n
1
, n Z
, m Z;
2
37

38.

справедлива формула
tg
а также формулы
tg tg
1 tg tg
ctg ctg 1
ctg
ctg ctg
ctg ctg 1
ctg
ctg ctg
(4.11)
(4.12)
(4.13)
38

39.

§5 Тригонометрические формулы двойного и
половинного угла
Тригонометрические формулы двойного угла
следуют из материала предыдущего
параграфа
cos 2 cos2 sin 2 ;
sin 2 2 sin cos ;
2tg
tg 2
1 tg 2
ctg 2 1
ctg 2
2ctg
39

40.

Рассмотрим два тождества:
1 cos
2
2
sin
2
2
(5.1)
,
и косинус двойного угла для :
cos cos
2
2
sin
2
2
.
(5.2)
Складывая их почленно, получаем
1 cos 2 cos
2
2
1 cos
cos
2
2
2
(5.3)
Вычитаем из (5.1) (5.2), получаем
1 cos 2 sin
2
2
40

41.

1 cos
sin
2
2
2
(5.4)
Разделим (5.4) на (5.3), получаем
tg 2
2
1 cos
1 cos
(5.5)
Если разделить равенство (5.3) на (5.4),
получаем
1 cos
ctg
2 1 cos
2
(5.6)
Можно получить и другие формулы для
вычисления тангенса половинного угла:
tg
2
sin
cos
2
2
sin
2
2 sin
2
cos 2 sin
2
2
2 sin 2
2 1 cos
sin
sin
sin
41

42.

1 cos
tg
2
sin
Т.е.
(5.7)
Аналогичным образом выводится формула
sin
(5.8)
tg
2 1 cos
§6 Выражение тригонометрических функций
через тангенс половинного угла
sin 2 sin
2
cos
2
2 sin
2
1
cos
2
2
2
sin
cos
:
cos
2 sin cos
2tg
2
2
2
2
2
2
2
2
2
2
cos 2 sin 2
1
tg
sin
cos
: cos
2
2
2
2
2
2
42

43.

Таким образом, получили формулу
sin
2tg
1 tg
(6.1)
2
2
2
Запишем формулу косинуса двойного угла
cos cos
2
2
sin
2
2
cos
2
cos
2
2
2
sin
2
sin
2
2
2
2
2
cos
sin
:
cos
1 tg 2
2
2
2
2
2
2
2
2
1
tg
sin
cos
: cos
2
2
2
2
cos
1 tg 2
1 tg 2
2
2
2
(6.2)
43

44.

Разделив, соотношение (6.1) на (6.2),
получаем
tg
2tg
1 tg
2
2
(6.3)
2
§7 Формулы суммы и разности
тригонометрических функций
Запишем формулы синуса суммы и
разности в новых обозначениях
sin u v sin u cos v cos u sin v
sin u v sin u cos v cos u sin v
44

45.

sin u v sin u v 2 sin u cos v
(7.1)
sin u v sin u v 2 cos u sin v (7.2)
Вводим обозначения
u
,
u v ,
2u ,
2
u v
2 v
v .
2
(7.3)
sin sin 2 sin
cos
2
2
(7.4)
sin sin 2 sin
cos
2
2
(7.5)
45

46.

По аналогии, запишем формулы косинуса
сумы и разности двух аргументов
cos u v cos u cos v sin u sin v
cos u v cos u cos v sin u sin v
Складываем и вычитаем эти выражения
cos u v cos u v 2 cos u cos v
cos u v cos u v 2 sin u sin v
В обозначениях (7.3) последние два равенства
примут вид
cos cos 2 cos
cos
(7.6)
2
2
(7.7)
cos cos 2 sin
sin
2
2
46

47.

Найдем сумму и разность тангенсов двух
аргументов
sin
sin sin sin cos sin cos sin
tg tg
cos cos
cos cos
cos cos
sin
tg tg
cos cos
(7.8)
sin
tg tg
cos cos
(7.9)
47

48.

§8 Преобразование произведений
тригонометрических функций
Воспользуемся уже известными равенствами
cos cos cos sin sin
cos cos cos sin sin
Почленно сложим равенства, получим
cos cos 2 cos cos
cos cos
cos cos
2
48

49.

Вычтем из первого равенства второе,
получим
cos cos 2 sin sin
cos cos
sin sin
2
Таким образом, получили две формулы:
cos cos
cos cos
2
(8.1)
cos cos
sin sin
2
(8.2)
49

50.

Теперь воспользуемся равенствами
sin sin cos cos sin
sin sin cos cos sin
Складывая их, получаем
sin sin 2 sin cos
следовательно,
sin cos
sin sin
2
(8.3)
50